大规模演化知识网络中的关联推理

赵泽亚 贾岩涛 王元卓 靳小龙 程学旗

1（中国科学院网络数据科学与技术重点实验室（中国科学院计算技术研究所） 北京 100190）2（解放军信息工程大学 郑州 450000）3（中国天绘卫星中心 北京 102012）（53414264＠qq．com）

大规模演化知识网络中的关联推理

赵泽亚1，2，3贾岩涛1王元卓1靳小龙1程学旗1

1（中国科学院网络数据科学与技术重点实验室（中国科学院计算技术研究所） 北京 100190）2（解放军信息工程大学 郑州 450000）3（中国天绘卫星中心 北京 102012）（53414264＠qq．com）

关联推理；演化知识网络；背包问题；链接延展模式；知识库

网络大数据时代，数据不再仅仅是简单的采集对象，其背后其实蕴含着大量丰富、复杂、关联的知识［1］．当前网络数据是广泛可用的，所缺乏的只是从中提取知识的能力．有效利用网络大数据价值的主要任务不仅仅是是获取越来越多的数据，也需要从已有的数据中挖掘更多有用的知识［2］，构建成知识库，便于对知识更充分地利用，因此基于网络的大规模知识库的构建是最近流行的一个研究方向，现有的大规模知识库有YAGO［3－4］，DBpedia［5］，Probase［6］等．

基于大规模知识库的关联推理是从海量信息中挖掘知识实现知识库增长的有效手段之一［7］，其主要目的是利用已有的大规模知识网络推理或者预测知识网络中隐含的关系．目前，关联推理已经在个性化推荐、社区发现、知识问答等方面得到广泛应用［8］．

现有的关于知识网络中关联推理的研究，采用的方法主要有有监督学习、半监督学习以及无监督学习等．目前的研究更多的是基于异构信息网络的关联推理，这里的异构信息网络包含多种不同类型的实体与关系，例如人物、地点、组织机构、电影、论文等，以及它们之间可能产生的各种类型的关系．现实中典型的异构信息网络有计算机科学文献网络DBLP和互联网电影资料库IMDB．

研究证明，在含有时间信息的异构网络中进行关联推理时，考虑时间信息得到的推理结果比未考虑时间信息得到的结果更好，例如文献［9－10］．同样地，由相关研究工作［11－12］证实，加入空间信息会对异构信息网络上的关联推理带来更大的提升．例如，文献［13］已证明，融合了空间信息的关联推理可以获得更好的推理结果，但是在文献［13］中的研究，仅仅考虑了一种类型实体间的关联推理，并非异构信息网络．目前，基于异构信息网络且对网络中的时空信息加以利用进行关联推理的相关研究还很少．

针对知识网络中时空信息的不断丰富，而现有的一些知识网络模型无法很好地刻画这些信息的问题，我们首先提出一个融合时间与空间信息的演化知识网络表示模型．与传统的异构信息网络不同，演化知识网络中的点和边都有相应的时间演化函数和空间演化函数，用于表示点和边上的时间信息和空间信息．利用这些时空函数可以详细刻画出现实中的实体自身的时空演化特点以及实体间关系的时空演变．例如在学术网络中，传统的异构信息网络只能推理多种类型的实体之间存在的不同类型的关系，却没有时序的概念，无法表达不同关系产生的先后顺序、关系存在的时间范围以及关系产生的地点等．这些信息对于关系预测和推荐是不可或缺的重要因素，且对于关联推理也具有重要意义．基于演化知识网络提出了一种新的关联推理方法．由于知识网络中的关联推理是知识挖掘的重要手段，而在知识挖掘中我们最关注的无疑是推理结果的正确性，因此我们提出新的关联推理方法旨在提高关联推理的准确率及对大规模数据的适应性．总结起来，本文贡献可归纳为以下2点：

1）提出了一个演化知识网络表示模型，将知识的时空信息融入到整个知识网络中，为知识的演化和计算提供更多的信息．

2）研究了基于演化知识网络的关联推理方法．具体讲，提出一种基于混合背包问题的关联推理方法KP－LIM，提高关联推理的准确率和推理效率．

实验证明，与当前流行的关联推理方法相比，我们提出的关联推理方法得到了更好的推理效果，在准确率上有8%～37%的提高，且在千万规模的数据集上的实验证明我们的方法依然有效．

下面详细介绍关联推理的相关研究工作．目前主流的关联推理方法是运用机器学习的算法进行关联推理，基本上可被分为2类：有监督学习方法［13－18］和无监督学习方法［10，19－21］．其中文献［13］是有监督学习方法的经典代表，它将关联推理问题当成一个分类问题，利用经典的逻辑回归方法训练模型实现关联推理．尽管有监督学习的方法比较流行，但是它们也存在许多弊端，例如训练复杂度高、平衡性较差、难以选择合适的特征等．相反，无监督的方法不需要关于数据分布的先验知识，避免了有监督学习的训练复杂度高等问题，对于大规模数据具有更强的适应性．无监督的方法主要是通过定义一些指标来刻画网络中实体间的相似度来实现关联推理，例如文献［19］是近期无监督关联推理的典型代表，它以经典的共同邻居（common neighbour，CN）方法为基础，加入节点连通性、边连通性以及部分时间信息等信息进行关联推理，但该方法只利用了网络中的局部信息．我们的提出的推理方法KP－LIM也是一种无监督学习方法，该方法定义了一个拓扑特征——链接延展模式（LE模式），将全图的结构特征以及网络中的时空间信息融入到背包问题的参数中，利用背包问题的求解对LE模式进行选择，再利用选出的模式实现关联推理．

另一方面，目前流行的关联推理方法大部分是应用于异构信息网络上的，即网络中的实体与边的类型是多种多样的，例如文献［9，15，22］等．近期又有许多工作将时间信息融入了异构信息网络中，并利用这些信息来提高关联推理的准确性．我们提出的演化知识网络模型既包含知识的时间信息也包含知识的空间信息，并利用这些信息进一步提高了关联推理的准确率．需要特别指出的是，YAGO2［4］中已经提出了一个基于时空信息知识网络的模型SPOTL，但是这个模型主要解决了YAGO2知识库上的知识检索与查询问题，并未将时空信息应用到关联推理问题上．

综上所述，由于现有的知识网络对于知识的时空信息的描述能力有限，导致在进行关联推理时无法对时空信息进行充分地利用，限制关联推理准确率的提高，因此我们提出一种融合了时空信息的知识演化网络模型，并提出一种基于该网络的推理方法，提高关联推理的准确率．

1 演化知识网络模型

本节我们主要提出一个演化知识网络模型和定义在该网络上的一种特殊的子网络——链接延展模式．

1．1 演化知识网络

演化知识网络是一个异构的演化的多重图，且图中的节点和边都包含时间与空间信息．具体定义如下：

定义1．演化知识网络．给定一个时间集合T，空间集合S，则演化知识网络GT，S可定义为一个8元组：

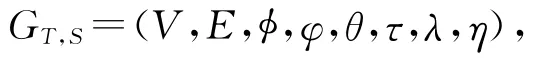
其中，V是演化知识网络中节点的集合；E有向边的集合，它的具体表示形式是一个3元组（u，v，r），这里u，v∈V，r∈R，其中R是边的所有类型构成的集合； ：V→A是节点类型的计算函数，使得每个节点通过该计算函数，可得到唯一的类型 （v）∈A，这里A为顶点的所有类型构成的集合；φ：E→R表示在边集合中某一条边的计算函数，且每一个实体对间最多有｜R｜条边；θ表示图中边的时间属性信息，用来描述一条边的发生以及存在的时间信息；τ是边的空间属性信息；λ是节点的时间属性信息，η是节点的空间属性信息．

在这个演化知识网络模型中，我们记录了图中节点与边的时间和空间信息．这里的时间信息是一系列离散的时间戳，空间信息则是一系列离散的地理位置信息．演化知识网络的可演化性主要体现在可通过感知网络中产生的新变化与自身进行比较，发现新知识，并实现自我更新．网络中的节点和边都有时间戳信息，它们都会随着时间的变化而演变，例如对于当前国家元首这个节点，会随着节点任职期满而自动更新为前任领导人，这便体现了网络的时空可演化性．

1．2 链接延展模式

基于我们提出的演化知识网络，本文着重研究在该网络上的关联推理问题．关联推理的主要目的是，利用知识库中已有的知识作为基础推理出两实体间可能存在的新关系．这里我们做的关联推理不仅仅要推理出新的边，还要给出边的类型．推理的主要思路是：首先构造出所有可能存在的链接延展模式；然后建立一个混合背包问题模型，将每一个模式看作背包问题中待选择的物品；通过背包问题的求解，选择出对于关联推理有意义的模式；利用这些模式在图中进行匹配，推理出新的关系．

首先引入演化知识网络中的链接延展（link extendable，LE）模式的定义，简称为LE模式．

定义2．链接延展模式．已知一个关系集R，知识网络GT，S，我们定义GT，S上的一个子网络H＝（V′，E′），V′ A，E′ R，在这个子网络中任意两节点都可通过一条边进行关联，如果这个子网络中有n个节点，则称其为n元模式，我们将这个子网络叫做链接延展模式．

由于子网络中节点的个数越多，计算复杂度越大且对关联推理的结果提升较小，因此本文重点研究3元模式．为了便于理解，下面我们简单列举一些典型LE模式．假设A′＝｛author（Au），paper（P）｝，R′＝｛write（w），cite（c）｝，若子网络中的点集为V′＝｛V1（Au），V2（P），V3（Au）｝，边集E′＝｛c（V1，V2），w（V3，V2），c（V1，V3）｝，则该LE模式由图1（a）表示；同理，若子网络为V′＝｛V1（P），V2（Au），V3（P）｝，E′＝｛w（V2，V1），c（V2，V3），c（V1，V3）｝，则该LE模式可刻画为图1（b）．

Fig．1Examples for LE－Patterns．图1 LE模式样例示意图

在真实的演化知识网络中，凡是满足LE模式要求的子网络均称为LE模式的实例h，例如图2（a）表示图1（a）的一个实例，图2（b）代表图1（b）的一个实例．

Fig．2 LE－Patterns instances．图2 不同LE模式的实例示意图

由图2可知，对于不同的LE模式的定义我们可以找到它相应的实例，且对于同一个LE模式可以有多个不同的实例．在进行关联推理时，我们需要将LE模式进行分解，使其成为可用来实现关联推理的新的LE模式．例如图2（a）表示的一个LE模式，我们可将其拆解为3个可用于关联推理的新的模式，如图3所示：

Fig．3 LE－Patterns for link prediction．图3 用于关联推理的LE模式示意图

在图3（a）中，我们将相连的两条边作为关联推理的条件，单独的一条边作为推理的结论．在进行关联推理时，若已知在3个节点他们的类型满足图3（a）中Au—P—Au的要求，且节点类型为Au—P和P—Au的节点对之间的关系分别为cite和write，则我们可推出两节点间存在cite关系．例如在图2（a）中，我们已知Tom和Lily类型为作者，paper1的类型为论文，且已知Tom引用了paper1，Lily写了paper1，则根据图3（a）中的LE模式，我们可推理Tom和Lily之间存在引用关系．需要指出的是，在网络中利用这些模式进行推理的结果并非全部正确，例如图1（b）所代表的模式的含义是，某一位作者写了2篇文章，可得出这2篇文章之间存在引用关系，而事实上这个引用关系可能不存在，因此，对于网络中包含的所有的模式构成的集合，我们需要利用背包问题的思想，从中选出置信度较高且涵盖关系类型更广泛的模式子集，并用子集中的所有模式进行关联推理．

2 关联推理方法

2．1 基于混合背包问题的关联推理方法（KP－LIM）

为了实现基于某一演化知识网络GT，S上的关联推理，首先需要找出网络中所有可能存在的可用于关联推理的模式，通过混合背包问题求最优解的思想对不同模式进行选择．

下面我们先简要介绍一下背包问题．背包问题（knapsack problem）是一种组合优化的NP完全问题，可以描述为：给定一组物品，每种物品都有自己的重量和价值，在限定的总重量M内，我们如何选择才能使物品的总价值最高．

这里我们将不同的模式看作背包问题中要装进背包中的物品，因此每个模式需要有相应的重量Weight和价值Value两个参数．我们从不同LE模式在网络中匹配的实例个数以及正确的实例个数的角度，给LE模式的2个参数重量Weight和价值Value做了以下定义．

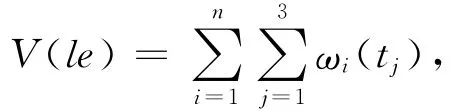
定义3．模式价值Value．已知演化知识网络GT，S，某一LE模式le的所有实例的集合H＝｛h1，h2，…，hn｝，其中包含n个不同实例，且每个实例中的每条边包含有该边产生的时间信息t，则le的价值V（le）为其中，ωi（t）代表某一条边产生的相对时间，即ωi（t）＝t－t0，t0为整个网络中边产生的最早时间．因此，LE模式的价值代表了LE模式对应所有实例间关系时间的和，即当LE模式对应的实例越多，且相应的实例发生的时间越靠后，该模式的价值越大．

定义4．模式重量Weight．已知一个LE模式中包含的3个关系为E1，E2，E3，若我们要用该LE模式对关系E3进行推理，首先通过遍历全图得到所有满足LE模式中节点类型和关系E1，E2要求的所有实例的个数为N，且这些实例中又满足LE模式中关系E3要求的实例的个数为n，则le的重量W（le）为

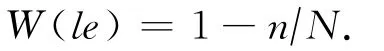
例如，由图1（a）表示的LE模式，若用它来推理作者间的引用关系，它在全图中所有匹配上另外2条关系规则的实例数量有100，其中2作者间存在引用关系的有99个实例，则该LE模式的重量为0．01．下面我们介绍如何将LE模式的选择问题建模成一个混合背包问题．

首先，根据要推理关系的类型的不同，将所有的LE模式分成k类，因此这里的k等于关系类型的总数．假设每一类中包含Ni（i＝1，2，…，k）个不同LE模式．为了满足所有关系类型都可以被推理出来，我们应在每个分类中至少选出一个LE模式．最终该问题可归纳为一个多重混合背包问题：

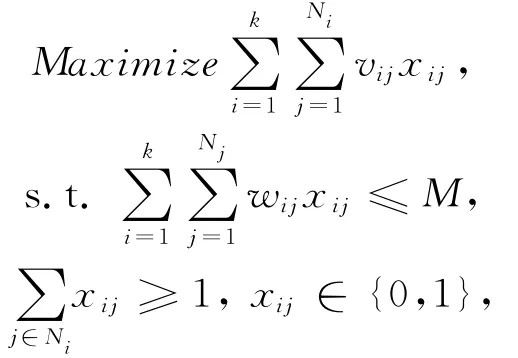
其中，xij表示对于第i个分类中的第j个LE模式，xij＝1表示选择该模式，xij＝0表示不选择该模式，vij表示该模式的价值，wij表示重量．

为了求解上面的混合背包问题，我们将问题拆解成2个0－1背包问题：1）多重选择背包问题，即在约束为耗费小于M＊（M＊＜M）条件下，从每个分类中选出一个结果，这个步骤主要是保证每个分类中都有一个LE模式被选择出来，即在后期做推理时，每种关系都可能被推理出来；2）常规的背包问题，在耗费小于M－M＊约束下我们可以从剩下的所有模式中选择更多意义的模式，提高推理的召回率．

2．2 算法及分析

实现关联推理的过程可主要分为以下3个步骤：1）构造可能存在的LE模式．已知演化知识网络GT，S上的边的所有类型，则任意3种类型的边的组合可构成一个候选LE模式．2）背包问题实现模式选择．遍历全图，找出不同模式相应的所有实例，计算得到不同模式的Weight和Value，通过混合背包问题的求解选出有意义的LE模式．3）利用选出的模式在网络中进行匹配得到推理结果．下面算法1中给出我们提出的关联推理算法的实现．

算法1．基于链接延展模式的关联推理．

输入：演化知识网络GT，S，待推理的实体对集合｛（n，n′）1，（n，n′）2，…，（n，n′）k｝；

输出：推理出的关系集合result．

由于在网络中实体间关系的类型的数量较少，因此LE模式的构造部分不是主要耗时的部分．分析可知整个关联推理过程的计算量集中在遍历全图找与模式相匹配的实例的过程，即算法1中调用的算法2．在算法2中我们采用一些优化技巧以提高效率，适应大数据环境的要求．下面我们给出算法2具体过程．

算法2．实例匹配与查找算法．

输入：演化知识网络GT，S，LE模式集SLE＝｛le1，le2，…，lem｝；

一般的遍历全图找不同模式的实例的方法是，对于每一个模式，遍历图中的所有节点；对于某一个节点，遍历它所有的边，如果满足模式要求，则以该边的另一个端点为起点遍历其他所有的边，看是否满足模式要求，依此类推．假设共有m个不同实例，全图有n个节点，且图中节点的平均出度入度和为r，则该运算的复杂度为O（mnr3）．以上方法虽然容易实现，运算复杂度却很高，效率低下，因此算法2利用了一些技巧降低了时间复杂度．

首先，我们不针对每个模式遍历一遍全图来找实例，而是做一个映射表，在这个映射表中不同模式对应的值为到当前为止该模式匹配上的实例个数，因此只需遍历一遍全图即可得到所有模式的实例个数．由于这里我们采用的模式均为3元模式，基于三角形的特殊构造，对于每个节点的具体匹配过程，我们不需要从一个节点出发，以广度优先的思想遍历3层关系，只需要从一个节点出发，找出它自身的所有关系，任意2个关系为一组，若这2个关系对的终点之间也存在关系则可构成一个LE模式，将映射表中的相应模式的value值加1即可．该算法经过优化后的时间复杂度为O（nr2）．

3 实 验

本节我们将详细介绍相关的实验结果，验证我们提出的基于混合背包问题的关联推理方法KPLIM的合理性与有效性，以及KP－LIM方法对于大数据环境的适应性．

3．1 实验数据集及参数选择

我们采用来自不同领域的数据构建成2个演化知识网络进行关联推理实验．这2个演化知识网络的数据分别来自于学术领域和电影领域，均包含了多种不同类型的节点和关系．其中学术网中的数据是从知名的学术文章网站Soscholar①上用网络爬虫爬取得到的，在这个网络中包含：1 000万个作者（A）、700万篇论文（P）、50万个杂志（M）、1．4万个会议（C）和5万个关键词（K）．我们选用论文的发表时间以及会议的召开时间作为网络中时间信息，选机构所在地构成网络中的空间信息．

对于电影网，它的数据主要来自于对知名电影网站IMDB上的电影信息的爬取．该网主要包括：演员（Ac）和导演（D）共4 530 159个，电影（M）2 132 383部，我们选取电影上映时间、拍摄地等信息作为电影知识网络的时间与空间信息．在表1和表2中分别列举了学术网和电影网中所有的实体间的直接关系．需要指出的是，表中罗列的是从元数据中抽取的直接关系．

Table 1 Direct Relations in the Scholar Network表1 学术网络直接关系表

Table 2 Direct Relations in the Film Network表2 电影网络直接关系表

①http：??www．soscholar．com?

表3中列举了一些学术网络中的常见的LE模式，其中第1列是待推理关系中2端节点实体的类型，第2列是待推理关系的类型，第3列是LE模式需要从网络中匹配实例的规则．在电影网中生成规则的方法与学术网相同，这里不再一一列举相应的LE规则．

Table 3 General LE－Rules in the Scholar Network表3 学术网络中常见的LE规则

对于学术网，已知边的类型数，则根据LE模式的特点可以找出所有可能存在的LE模型，去掉一些不可能存在的模式，最终，对于学术网我们可得到了124个不同的模式．同理对于电影网，我们共得到18个模式．

实验过程中，我们在图中随机隐藏掉占整个网络中所有关系数量的指定比例的关系以及它们所有的附加信息，实验过程中通过改变这个比例来比较不同方法的推理能力，这里由于我们做的是关联推理，而不是关系预测或时序关联推理，因此在隐藏关系时不考虑关系的时间顺序．为了验证我们提出的方法的有效性，在实验中我们将KP－LIM方法与2种最近比较流行的关联推理方法进行比较，一个是经典的有监督算法的代表逻辑回归方法［14］（简称Logistic），另一个是文献［8］中提出的方法M－CN＋ANC＋OAWpress（简称CN），它是一种典型的无监督学习方法．对于逻辑回归方法，我们是将每一个LE模式作为一维特征，构造训练数据，通过逻辑回归算法进行学习，学出每个特征的系数，在进行关联推理时给出一个实体对，匹配不同的模式．如果没有模式可以匹配上，则推理两节点间没有关系；如果有模式匹配上则不同的关系可以得到一个分数，当分数大于某一阈值时，我们推理这两节点间存在这种关系．实验可得，当阈值选择为0．6时，逻辑回归的推理效果最好，因此在后面的比较实验中，我们选择阈值为0．6．而对于CN方法，在给出实体对后，针对每种关系可计算出一个得分．同理我们选择一个阈值，当得分大于该阈值时，推理两实体间存在某一关系，实验可知当阈值选择0．8时效果最好．

对于KP－LIM模型，在背包问题中有2个参数需要确定，背包问题的总体约束值M＞0和多重选择背包问题的约束条件M＊，对于M＊有一个宽泛的约束是0＜M＊＜M，而事实上我们对M＊给出一个更为严格的约束，即对于每一个模式分类，找出一个耗费最小的模式，则M＊应大于所有分类中最小耗费值之和，用公式可表示为

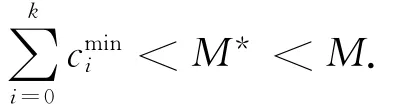
对于M的值，也有一个更为严格的约束，即所有模式的耗费之和，对于学术网M值的上限Mmax是10．2，对于电影网的Mmax是4．15．

为了确定M＊和M的具体值，我们首先固定M的值、变更M＊的值，来研究M＊的值变化对于关联推理效果的影响，找出推理结果最优时M＊的值；然后固定M＊的值，在（M＊，Mmax）的范围内调节M的值，找出推理结果最优的M值，最终可通过实验确定出2个参数的值．图4给出了对学术网进行参数调节的过程，其中图4（a）～（d）分别代表M＝6，7，8，10时对M＊的值进行调节得到的测试结果．从图4可知，当M＝7，M＊＝5时，对于学术网上的关联推理结果最好．同理我们对电影网上的数据进行测试，得到当M＝3，M＊＝2时结果最优．

3．2 实验结果及分析

本节我们会通过实验进行3方面的比较：1）比较KP－LIM与Logistic和CN方法间的关联推理准确率；2）演化知识络网与传统的异构信息网络的比较；3）KP－LIM算法对于大数据的适应性的性能测试．

3．2．1 不同关联推理方法的推理效果比较

在进行不同关联推理方法的比较实验时，我们选择准确率作为评价指标，主要是因为基于大规模知识网络的关联推理，推理结果的正确与否具有决定性作用，推理结果作为知识必须要保证其准确性，因此这里我们选准确率作为指标．

实验结果如表4所示，主要比较了3种不同方法的准确率，在这里α表示隐去的关系数量占全图关系总数量的比例．随着α的增加，KP－LIM方法的表现均优于其他2种方法，与有监督算法Logistic相比，我们的方法在学术网上准确率获得了2%～62%的提高；对于CN方法，我们的方法获得了28%～70%的提高，平均提高量分别为29%和37%．同理在电影网上，我们的方法分别获得了和1%～22%和20%～30%的提高，平均提高值分别为8%和24%．综合以上结果可得出结论，KP－LIM方法在不同的数据集上，比当前比较流行的2种方法均取得更好的推理结果．其主要原因是，我们的方法将不同模式的特点以及全图的背景知识信息融入到背包问题中，通过背包问题的求解，从模式集合中选出高质量的模式进行关联推理；而Logistic采用了所有的模式，仅仅通过训练数据给不同的模式学习出不同的系数，既未将全部的背景知识信息加以利用，模型的好坏完全受训练数据好坏的影响，又未对模式进行筛选；而CN方法只考虑了待推理的2个实体的相关关系，对图的结构信息利用不充分，因而它的准确率最低．

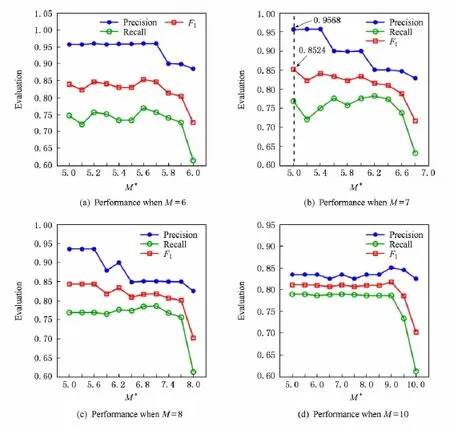
Fig．4 Parameter tuning on the scholar network．图4 学术网调参结果

Table 4 Precision Obtained by Using Different Inference Methods表4 不同关联推理方法准确率值的比较%

3．2．2 演化知识网络与传统网络的比较

在3．2．1节中我们通过实验证明了KP－LIM与其他几个关联推理中的经典方法在准确率上有较大的提高，其功于我们提出的基于混合背包问题的模式选择策略色优越性，同时我们猜想演化知识网络模型自身也对与推理结果的准确率的提高有一定的帮助．因此，我们分别在演化知识网络（EKN）和异构信息网络（HIN）中采用KP－LIM方法进行关联推理，比较2个网络中的推理效果．在2个网络中，我们分别隐掉相同的关系，再对这些关系类型进行推理，由于传统的异构信息网络中没有时间信息，因此只能采用弱化的KP＿LIM方法进行模式选择，即模式价值的定义有所改变，改为与该模式所有匹配的实例的个数．推理结果如图5所示：

Fig．5 Link inference on different networks．图5 不同网络中的关联推理比较

由图5可知，随着隐掉边的比例的变化，EKN上的推理准确率始终比HIN高，提高比例为1．9%～87%．由此可见，演化知识网络与异构信息网络相比对关联推理有一定的帮助，这主要是因为演化知识网络中包含点与边的时空信息，这些信息对于关联推理的准确率的提高具有重要意义．值得注意的是，随着隐掉边的比例的增加，两者的推理准确率均呈下降趋势，这是由于隐掉边的比例越大，已有的可用于推理的知识越少，因此推理的准确率有一定的下降．

3．2．3 KP－LIM的性能测试

由于在大数据环境下，数据量急剧增长，能否适应大数据的挑战，也是衡量一个算法好坏的重要方面，因此，下面我们对KP－LIM方法的计算性能进行测试．首先分别构造不同大小的知识网络，测试在不同规模的网络上KP－LIM进行关联推理的时间消耗，这里我们将网络中的点的数量从100万逐渐增加到1 000万，并记录下推理时间的变化，如图6所示．

由图6可知，随着网络规模的迅速增加，我们提出的KP－LIM推理方法时间消耗的增长缓慢．当网络规模扩大了10倍，推理耗时仅从8．372s增加到15．726s．在算法2我们也对KP－LIM方法的时间复杂度进行了分析，该算法的主要时间消耗集中在遍历全图找不同模式实例的过程，复杂度为O（nr2），这里n代表网络中节点的个数，r为节点的出入度，因此随着网络规模的增加，r的变化较小，因此整个算法的时间消耗主要受到网络中节点的个数n的影响，因而随着网络规模的增加算法的时间消耗呈线性增长．综上所述，我们提出的关系KP－LIM不仅在推理准确率上取得了较好的结果，其计算成本也并没有对着网络规模的扩大而呈指数增长，因此KP－LIM的计算性能也能够满足大规模知识网络对关联推理性能与效率的要求．

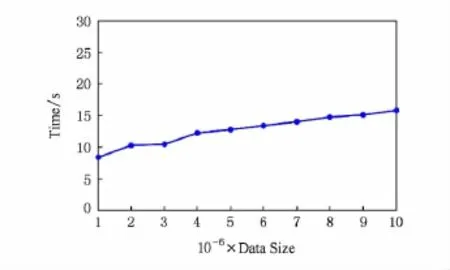
Fig．6 The change of time consumption with the increase scale of relation network．图6 随着网络规模的增加关联推理的时间消耗

4 总结与展望

本文首先提出了一个融合了时间与空间信息的演化知识网络，基于该网络提出了一种关联推理方法．实验证明我们的方法比当前流行的一些关联推理方法取得了更高的准确率，且在大数据的环境下依然拥有较好适应性．但该KP－LIM方法也存在一定的局限性，例如对于网络中已有的关系数量有一定的依赖性、无法很好地应对冷启动问题，且对于网络中的空间信息利用不够．

因此，关于这个工作，仍有以下4个需要研究的方向：1）KP－LIM方法对知识网络中已有的关系数量的依赖性较强，当面对冷启动问题时，如何保证推理的准确率有待进一步研究；2）对于演化知识网络中的空间信息的利用有限，下一步可研究如何更充分地利用网络中的时空信息，进一步提高推理效果；3）从知识表示的角度，研究知识网络的演化性和关联推理，是近年来知识网络的关联推理研究的新方向，相关工作包括文献［23］；4）研究时序关系的推理，即推理知识网络中关系产生的时间，是进一步研究知识网络演化性的又一重要方向，相关工作包括文献［24］．

［1］Wang Yuanzhuo，Jia Yantao，Liu Dawei，et al．Open Web knowledge aided information search and data mining［J］．Journal of Computer Research and Development，2015，52（2）：456 474（in Chinese）（王元卓，贾岩涛，刘大伟，等．基于开放网络知识的信息检索与数据挖掘［J］．计算机研究与发展，2015，52（2）：456 474）

［2］Wang Yuanzhuo，Jin Xiaolong，Cheng Xueqi．Network big data：Present and future［J］．Chinese Journal of Computers，2013，36（6）：1125 1138（in Chinese）（王元卓，靳小龙，程学旗．网络大数据：现状与挑战［J］．计算机学报，2013，36（6）：1125 1138）

［3］Lujun F，Anish D S，Cong Y，et al．Rex：Explaining relationships between entity pairs［J］．VLDB Endowment，2011，5（3）：241 252

［4］Suchanek F M，Kasneci G，Weikum G．Yago：A large ontology from Wikipedia and wordnet［J］．Web Semantics：Science，Services and Agents on the World Wide Web，2008，6（3）：203 217

［5］Hoffart J，Suchanek F M，Berberich K，et al．YAGO2：A spatially and temporally enhanced knowledge base from Wikipedia［C］??Proc of the 23rd Int Joint Conf on Artificial Intelligence．Menlo Park，CA：AAAI，2013：3161 3165

［6］Jia Yantao，Wang Yuanzhuo，Cheng Xueqi，et al．OpenKN：An open knowledge computational engine for network big data［C］??Proc of the 2014Int Conf on Advances in Social Networks Analysis and Mining（ASONAM 14）．Los Alamitos，CA：IEEE Computer Society，2014：657 664

［7］Lin Hailun，Jia Yantao，Wang Yuanzhuo，et al．Populating knowledge base with collective entity mentions：A graphbased approach［C］??Proc of the 2014Int Conf on Advances in Social Networks Analysis and Mining（ASONAM 14）．Los Alamitos，CA：IEEE Computer Society，2014：504 611

［8］Cheng Xueqi，Jin Xiaolong，Wang Yuanzhuo．Survey on big data system and analytic technology［J］．Journal of Software，2014，25（9）：1889 1908（in Chinese）（程学旗，靳小龙，王元卓．大数据系统和分析技术综述［J］．软件学报，2014，25（9）：1889 1908）

［9］Lee J B，Adorna H．Link prediction in a modified heterogeneous bibliographic network［C］??Proc of the 2012 Int Conf on Advances in Social Networks Analysis and Mining（ASONAM 12）．Los Alamitos，CA：IEEE Computer Society，2012：442 449

［10］Rossetti G，Berlingerio M，Giannotti F．Scalable link prediction on multidimensional networks［C］??Proc of the 11th Int Conf on Data Mining Workshops（ICDMW 11）．Los Alamitos，CA：IEEE Computer Society，2011：979 986

［11］Cho E，Myers S A，Leskovec J．Friendship and mobility：User movement in location－based social networks［C］??Proc of the 17th ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining．New York：ACM，2011：1082 1090

［12］Wang Dashun，Pedreschi D，Song C，et al．Human mobility，social ties，and link prediction［C］??Proc of the 17th ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining．New York：ACM，2011：1100 1108

［13］Crandall D J，Backstrom L，Cosley D，et al．Inferring social ties from geographic coincidences［J］．National Academy of Sciences，2010，107（52）：22436 22441

［14］Popescul A，Ungar L H．Statistical relational learning for link prediction［C?OL］??Proc of the 18th Int Joint Conf on Artificial Intelligence．Acapulco，Mexico：IJCAI，2003［2016－01－05］．http：??www．cis．upenn．edu?～ungar?papers? popescul?statistical03link．pdf

［15］Sun Yizhou，Barber R，Gupta M，et al．Co－author relationship prediction in heterogeneous bibliographic networks［C］??Proc of the 2011Int Conf on Advances in Social Networks Analysis and Mining（ASONAM 11）．Los Alamitos，CA：IEEE Computer Society，2011：121 128

［16］Sun Yizhou，Han Jiawei，Aggarwal C C，et al．When will it happen？：Relationship prediction in heterogeneous information networks［C］??Proc of the 5th ACM Int Conf on Web Search and Data Mining（WSDM 12）．New York：ACM，2012：663 672

［17］Tang Jie，Lou Tiancheng，Kleinberg J．Inferring social ties across heterogenous networks［C］??Proc of the 5th ACM Int Conf on Web Search and Data Mining（WSDM 12）．New York：ACM，2012：743 752

［18］Jia Yantao，Wang Yuanzhuo，Li Jingyuan，et al．Structuralinteraction link prediction in microblogs［C］??Proc of the 22nd Int Conf on World Wide Web Companion（WWW 13）．New York：ACM，2013：193 194

［19］Davis D，Lichtenwalter R，Chawla N V．Multi－relational link prediction in heterogeneous information networks［C］??Proc of the 2011Int Conf on Advances in Social Networks Analysis and Mining（ASONAM 11）．Los Alamitos，CA：IEEE Computer Society，2011：281 288

［20］Liu Dawei，Wang Yuanzhuo，Jia Yantao．LSDH：A hashing approach for large－scale link prediction in microblogs［C］?? Proc of the 28th AAAI 14．Palo Alto，CA：AAAI，2014：3120 3121

［21］Zhao Zeya，Jia Yantao，Wang Yuanzhuo．Content－structural relation inference in knowledge base［C］??Proc of the 28th AAAI 14．Palo Alto，CA：AAAI，2014：3154 3155

［22］Yang Yang，Chawla N V，Sun Yizhou，et al．Predicting links in multi－relational and heterogeneous networks［C］?? Proc of the 13th Int Conf on Data Mining Workshops（ICDM 12）．Los Alamitos，CA：IEEE Computer Society，2012：755 764

［23］Jia Yantao，Wang Yuanzhuo，Lin Hailun，et al．Locally adaptive translation for knowledge graph embedding［C］?? Proc of the 30th AAAI 16．arXiv preprint arXiv：1512．01370［24］Zhao Zeya，Jia Yantao，Wang Yuanzhuo，et al．Temporal

link prediction based on dynamic heterogeneous information

network［J］．Journal of Computer Research and

Development，2015：52（8）：1735 1741（in Chinese）

（赵泽亚，贾岩涛，王元卓，等．基于动态异构信息网络的时

序关系预测［J］．计算机研究与发展，2015，52（8）：1735

1741）

Wang Yuanzhuo，born in 1978．PhD，associate professor．IEEE member and senior member of China Computer Federation．His current research interests include social computing，open knowledge network，network security analysis，stochastic game model，etc．

Zhao Zeya，born in 1990．Master．Her main research interests include open knowledge engineering，data mining，social computing．

Jia Yantao，born in 1983．PhD，assistant professor．His main research interests include open knowledge network，social computing，combinatorial algorithms．

Jin Xiaolong，born in 1976．Associate professor，PhD supervisor．His research interests include social computing，multiagent systems，performance modelling and evaluation，etc．

Cheng Xueqi，born in 1971．Professor，PhD supervisor．His research interests include network science，Web search ＆data mining．

Link Inference in Large Scale Evolutionable Knowledge Network

Zhao Zeya1，2，3，Jia Yantao1，Wang Yuanzhuo1，Jin Xiaolong1，and Cheng Xueqi11（Key Laboratory of Network Data Science ＆Technology（Institute of Computing Technology，Chinese Academy of Sciences），Beijing100190）2（The PLA Information Engineering University，Zhengzhou450000）3（TH－Satelite Center of China，Beijing102012）

In the era of network big data，the spatiotemporal information of knowledge is richly stored in knowledge networks，such as the building time of links，the lifetime of vertices，etc．Traditional knowledge network representation models are mostly blind to either the spatial or the temporal information of vertices and links in the network．It has been verified in the literature that considering the spatial or the temporal information of vertices and links can promote the performance of link inference in knowledge networks．In this paper，we propose an evolutionable knowledge network model，i．e．，a heterogeneous knowledge network，in which vertices and edges are anchored in both time and space dimensions．Then based on the model，we further study the link inference problem on evolutionable knowledge networks．Specifically，we firstly define the link extendable patterns to characterize the link formation process，and then propose a knapsack constrained link inference method to turn the link inference problem into a combinatorial optimization problem with the knapsack－like constrains．The dynamic programming technique is used to solve the optimization problem in pseudo－polynomial time complexity．Experiments on real data sets suggest the better effectiveness and scalability of our proposed method over large－scale networks than the state－of－the－art methods．

link inference；evolutionable knowledge network；knapsack problem；link extendable（LE）pattern；knowledge base

TP182

2014－11－24；

2015－03－13

国家“九七三”重点基础研究发展计划基金项目（2014CB340405，2013CB329602）；国家自然科学基金项目（61173008，61232010，61303244，61402442）；北京市科技新星计划项目（Z121101002512063）；国家科技支撑计划项目（2012BAH39B04）；北京市自然科学基金青年基金项目（4154086）

This work was supported by the National Basic Research Program of China（973Program）（2014CB340405，2013CB329602），the National Natural Science Foundation of China（61173008，61232010，61303244，61402442），Beijing Nova Program（Z121101002512063），the National Key Technology Research and Development Program of China（2012BAH39B04），and the Natural Science Foundation of Beijing（4154086）．

摘 要 网络大数据时代的到来使得知识网络中时空信息越来越丰富．现有的知识网络描述模型对知识的时空信息刻画不足．研究证明，利用网络中知识的时空信息以及相关性，能够提高网络中知识间的关联推理的准确率．针对以上问题，首先提出了一种包含时空信息的演化知识网络表示模型，然后研究在该网络模型上的关联推理问题，提出了一种基于背包问题的知识间关联推理方法．在多个数据集上的实验证明了所提出的关联推理方法的有效性以及对大规模知识网络的适应性．