Curvelet变换在图像增强中的应用

钟满田

（罗定职业技术学院，广东 罗定 527200）

Curvelet变换在图像增强中的应用

钟满田

（罗定职业技术学院，广东 罗定 527200）

为探索Curvelet变换在含噪声图像增强中边缘处处理性能，借用MATLAB软件平台，通过对含噪声图像分别用小波变换和Curvelet变换进行计算机模拟仿真实验，对比实验图得出Curvelet变换比小波变换在图像边缘处处理效果更为优越的结论。

Curvelet变换；图像增强；边缘

近几年，虽然在图像处理中标准的小波变换已经取得了很大成效，但是它在水平和垂直方向上建立起来的基函数的空间各向同性限制了它的表示图像的效率。对于我们人类视觉感知特别重要的一维不连续点处——图像的边缘和轮廓，间断了非常多的小波基函数，且只能由一个非稀疏的图表示。因此，我们就需要一个更加复杂的多方向(M-DIR) 和各向异性的变换，目的是为了更有效地获取除了水平垂直之外的更多方向的几何结构来刻画图像的各向异性。[1]

鉴于边缘处理技术在图像分析和理解中有着非常重要的地位，增强对比度很好方法之一就是增强边缘。在过去，传统的边缘增强方法总体可划分为两种：一种是频域的高通滤波方法，另一种是空间域基于模板的方法，但是它们的处理效果都不够理想。虽然小波变换借助于其多分辨率以及其去相关性等特点可以成功地运用于图像边缘增强，但是小波的增强方法有其明显的局限性，那就是由于它并不太适合于检测、获取各向异性的图像各个元素，此外小波增强更会平滑掉图像的部分细节元素。与此相反，对新的多尺度体系Ridgelet 和 Curvelet 而言，由于它们有对方向敏感的基函数，且属于相当高度的各向异性变换，因此对于所需的边缘很重要的图像增强应该具有非常大的优势。[1]

1 离散Curvelet变换

为了能更好地说明离散Curvelet变换由来，这里先引用一个定义和定理。

定义1∶ Curvelet 变换是将任意均方可积函数f映射为系数序列αμ（μ∈m）的变换。其中M表示αμ的参数集，称元素σμ=△SψQ,a,a∈Γ为Curvelet。[1]

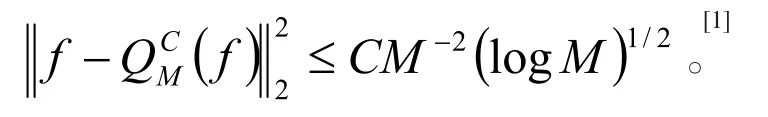
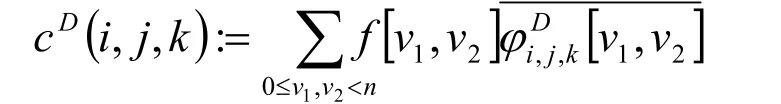
并且用此函数来实现多尺度分割，从而有对于每个W=（W1，W2），W1＞0，均有

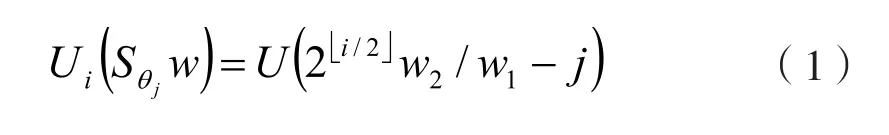
2 Curvelet变换的实现

Curvelet变换方法的核心思想就是围绕原点wrap，也就是说对任意区域在具体实现时，都是通过周期变化技术一一对应到原点的仿射区域。具体过程如下：[1][2][3][4][5]

（1）对于给定的二维函数在笛卡尔坐标下进行2DFFT变换，可以获得二维频域表示

（2）在频域区域，对于每一对（尺度，角度）用(i，f)表示，经过重采样获得采样值

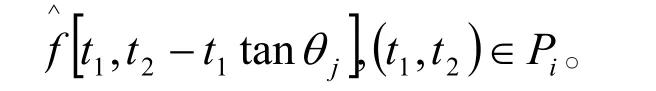
（3）将内插后 乘以窗函数 可得

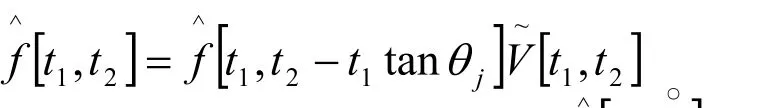
3 计算机仿真实验

3.1 图像计算机仿真实验

借助于MATLAB7.0软件平台，对含噪声的彩色数字图像分别采用小波变换和Curvelet变换进行计算机仿真实验，所得到的实验图像如图1所示。

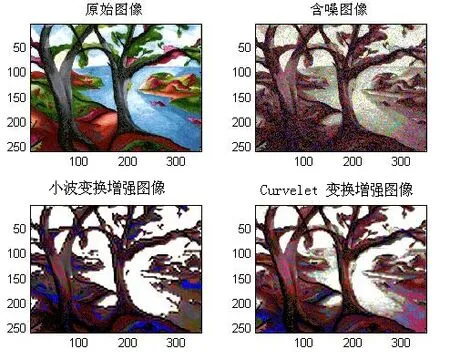
图1 两种变换增强图像

3.2 结构、统计和特征分析

经过变换后得到结构的系数为 ，其中i表示尺度，j表示方向， 表示第j个方向尺度层上的矩阵坐标。512×512 的图像的具体系数格式如表1所列。

表1 小波变换和Curvelet 变换系数结构

从表1可以看出，一个512 ×512 的图像经过小波和Curvelet 变换后，都被划分成为6 个尺度层。第一层称为最内层Coarse 尺度层，是由低频系数组成的一个矩阵；第六层称为最外层Fine 尺度层，是由高频系数组成的一个的矩阵；中间的第二层至第五层称为Detail 尺度层，分割每层系数为4 个大方向，划分每个方向上为4个、8 个、16 个小方向，它们都是矩阵形式且由中高频系数组成。从表中显然可以看出，在矩阵点Curvelet 变换较小波变换更为细化，从为边缘处理提供绝不可少的条件。

统计每层的能量、最大值、最小值、均值和方差，其中以计算每层系数的绝对值的平方求和作为能量，统计结果如表2所示。

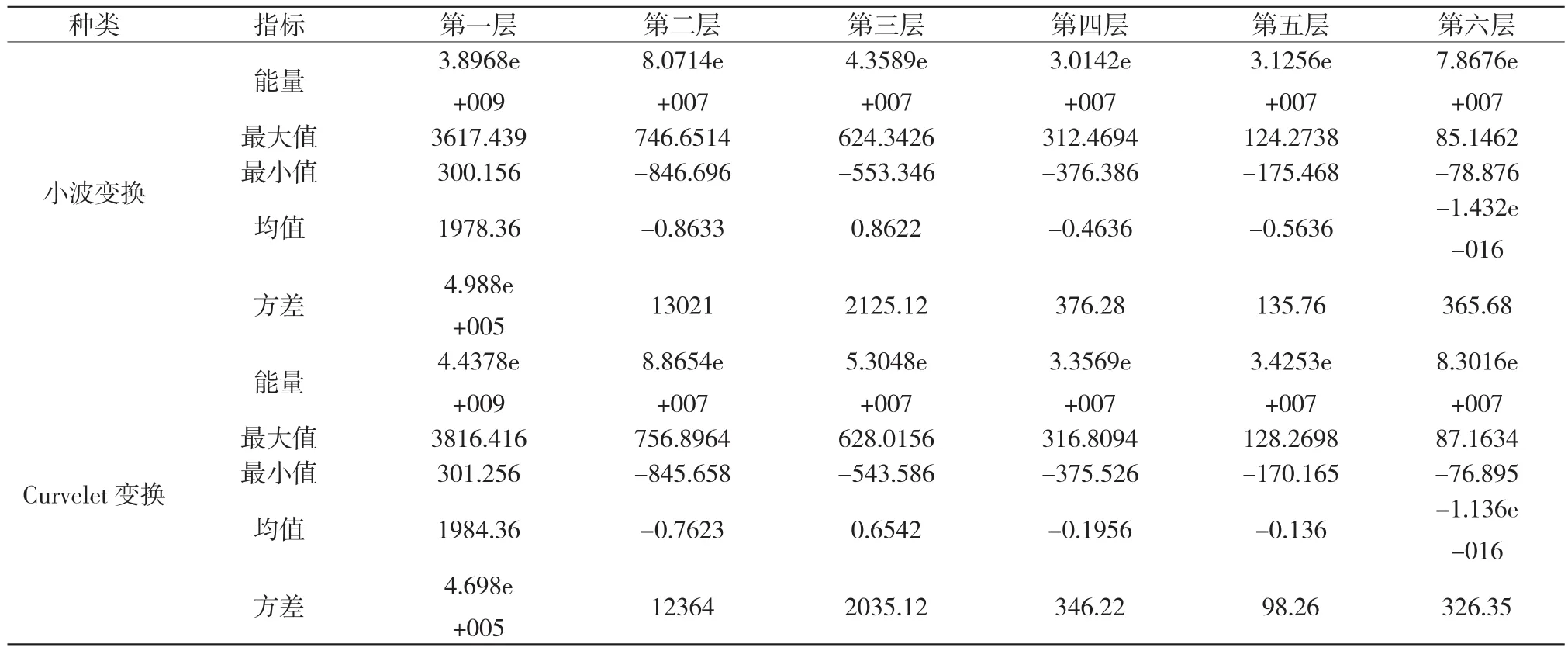
表2 小波变换和Curvelet变换系数统计

从表2可以明显的看出，在各层的能量、最大值、最小值、均值和方差等指标方面，Curvelet变换较小波变换好；从图1可以明显看出，在增强图像的边缘处，小波变换有非常明显的呈锯齿状，但是Curvelet变换的增强图像边缘处为光滑，与原始图像非常接近。

3.3 Curvelet变换图像增强其它实例

再次借助于MATLAB7.0软件平台，对含噪声的普通照片和位图图片分别采用小波变换和Curvelet变换进行计算机仿真实验，所得到的实验图像如图2、图3所示。

图2 两种变换增强照片

图3 两种变换增强位图

通过计算机仿真实验结果的对比，可以知道Curvelet变换与小波变换相比较，得出的结论和前面彩色数字图像是一样的，总体上Curvelet变换可以很接近于原始图像效果，说明Curvelet变换图像增强是可行的。

4 结束语

从仿真实验的图像和数据统计分析知，Curvelet变换比小波变换在图像增强尤其是图像的边缘处更有优势。所以，Curvelet变换的图像增强算法可以用于高质量的航空航天领域的数字图像处理、生物医学的显微光学图像进行处理和分析、机械零部件的检查和识别等工业生产的自动化设计和产品质量检验、指纹和人脸等生物特征的增强处理等社会安全管理方面。

[1]闫敬文，屈小波.分析及应用[M].北京:国防工业出版社，2008.

[2]降刚，肖棋，陈学俭. Curvelet 变换在图像处理中的应用综述[J].计算机研究与发展， 2005，42(8) : 1331-1337，2005.

[3]葛哲学，陈仲生.MATLAB时频分析技术及其应用[M].北京:人民邮电出版社，2006.

[4]成礼智，郭汉伟.小波与离散变换理论及工程实践[M].北京:清华大学出版社，2005.

[5]张德丰.MATLAB分析[M].北京:机械工业出版社，2012.

[6]王国秋，袁卫卫.一般的9-7小波滤波器及其图像压缩性能研究[J].电子学报，2001，29(1).

[7]周伟.MATLAB小波分析高级技术[M].西安:西安电子科技大学出版社，2006.

[8]邸继征.分析原理[M].北京:国防工业出版社，2010.

[9]焦李成，谭山.图像的多尺度几何分析：回顾和展望[J].电子学报，2003，31(12A):1975-1981.

[10]朱希安，曹林.小波分析及其在数字图像处理中的应用[M].西安:电子工业出版社，2012.

Application of Curvelet Transform to Image Enhancement

ZHONG Man-tian
(Luoding Polytechnic, Luoding 527200, China)

In order to explore the edge processing performance of Curvelet transform in noisy image enhancement,this paper uses the MATLAB software platform to conduct a simulation experiment of the noisy image respectively with wavelet transform and Curvelet transform. The experiment arrived at a conclusion that Curvelet transform is more superior to the wavelet transform in image edge processing effect.

Curvelet transform; image enhancement; edge

TP391.41

A

1672-2841（2016）02-0035-04

2015-12-28

钟满田，男，讲师，硕士，研究方向为数学与计算机模拟。