相似涨落差径流预报模型及应用

卫小筠，黄定波，张夔飞，郑程遥

（1.广州市恩莱吉能源科技有限公司，广东 广州 510655；2. 清远粤华电力有限公司，广东 清远 511500；3. 广东水利电力职业技术学院，广东 广州 510925）

相似涨落差径流预报模型及应用

卫小筠1，黄定波1，张夔飞2，郑程遥3

（1.广州市恩莱吉能源科技有限公司，广东 广州 510655；2. 清远粤华电力有限公司，广东 清远 511500；3. 广东水利电力职业技术学院，广东 广州 510925）

水文预报的涨落差法，其传播时间由于洪水特性不同而变化，上、下游涨落差的比例因子kh及kq影响因素较为复杂，使得涨落差模型由于其非线性问题而影响预报精度。当水文观测数据足够时，识别出与现时上游断面涨落过程相似的同断面历史涨落过程，通过与此对应的下游断面历史涨落过程，识别出现时下游断面预报的径流参数，如水位、流量等。由此，构建了相似涨落差径流预报模型，通过清远观音洲水电站的应用，表明了模型可获得较高的预报精度。

水文径流预报；扩散波；涨落差法；水文相似分析

涨落差法是在我国应用约60年历史的一种经验方法，由于其采用上、下游水位的涨落差建立水文关系，避免了直接涉及水深和断面面积等随河道冲淤会产生变化的因数，因此在大江、大河干流的洪水预报中，精度较高。如1998年长江、松花江特大洪水期间，应用此方法对洪峰水位和洪水过程进行了成功的预报[1]。

但是，当预报不是在大江大河的干流，预报对象不仅仅是洪水，而且也包括水资源优化调度所需的一般径流参数，则涨落差法相关参数的非线性问题引起的预报误差较大。因此，应独辟蹊径，使这种成熟的、简单的方法应用于一般的径流预报。

詹道江、叶守泽指出[2]，河段洪水预报是以河槽洪水运动波理论为基础，由河段上游断面水位、流量过程预报下游断面的水位和流量过程，其实质是以水文学途径近似求解河道非恒定流。在此，首先从明槽非恒定流的Saint Venan方程出发，推导涨落差法的基本方程，从而明确涨落差法有关参数的物理本质，继而对涨落差法的影响因素进行分析，用水文过程的相似性为基础，消除一些分散的、非线性参数的影响，足够精确的识别出预报数据，如水位、流量等，构建的模型称为相似涨落差径流预报模型。该模型在广东清远北江枢纽观音洲水电站径流预报中得到了成功的应用。

1 涨落差法

为简单计，讨论无支流河流。

根据方程，在无支流汇入河段的连续性方程和运动方程分别为：

式中：Q为流量，A为过水面积，v为流速，z为水位，hf为摩擦损失，x为河槽距离。对于非恒定流，各水力学参数皆为时间t与距离x的函数，如Q=Q(x,t)，A=A(x,t)，在此仅简记为A、Q，其他变量同样处理，不赘述。

设y为水深，io为槽底坡度，摩阻坡度，则运动方程（2）可表示为：

式（3）中，左边各项依次称为当地惯性项、对流惯性项、附加比降、摩阻比降和河底比降。其中前两项对汇流影响较小，一般情况下可以忽略[3]，而仅计后三项，称此刻的偏微分方程为扩散波，Saint Venan方程变为：

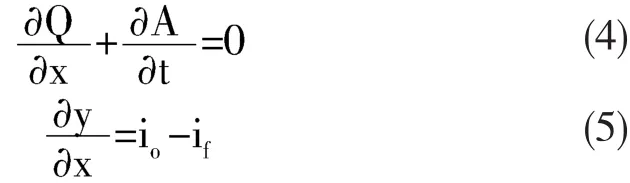
非恒定流的if目前还缺乏深入研究，暂按恒定渐变流沿程水头损失计算，则：

式（6）中，v为流速，C为谢才系数，R为水力半径。

设河道为宽浅矩形河槽，B= B(x)为河槽宽度，由水力学相关参数关系联立式（4）～（6），可得河道汇流洪水波扩散方程。

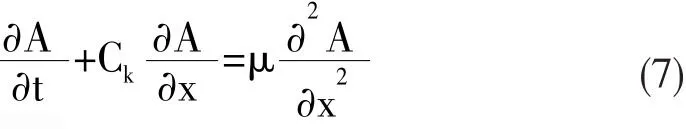
式（7）中

由于A=A(x,t)

则：

比较式（7）与式（8），则式（7）等价于以下方程组，

由此，可称Ck为洪水波波速，μ为洪水波扩散系数。式（9）表明，沿特征线河道断面衰减值近似的，经过为上下游断面距离）时间后，下游过水断面面积为：

后续的推导见文［1］，为连贯的讨论，摘录如下：

将μ值代入式（10）得：

同理

进而有：

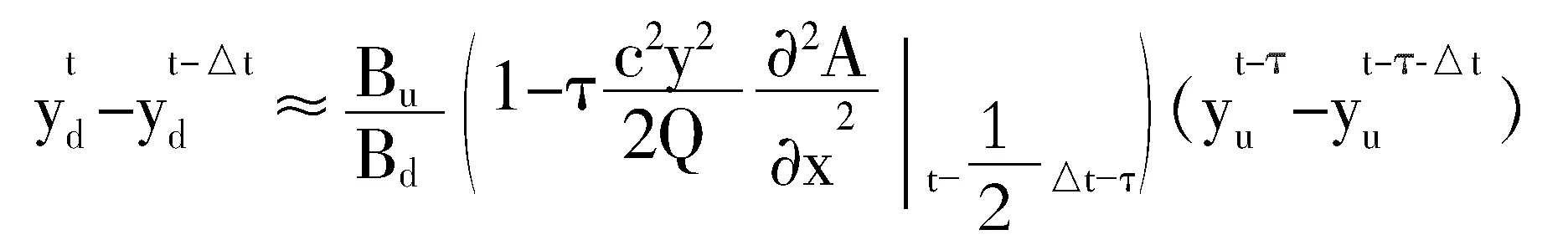
式中，Bu为上游断面水面宽；Bd为下游断面水面宽；Yd为下游断面t时刻水深；为下游时刻水深； 为上游t-τ时刻水深；为上游断面时刻水深。

令：

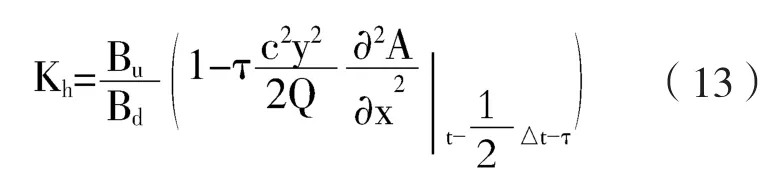
则得

考虑水深差即水位差，且非恒定流中水位与流量的相关关系可得：

由推导过程可看出，涨落差法实质是以水文学途径，用动力波理论为基础，近似求解非恒定流的一种预报方法，有着可靠的物理基础。

从式（15）或（16）可得出涨落差法的预报步骤为：首先测出上游断面在t-τ-△t时刻的水位（流量），其次测出上游断面在t-τ时刻的水位（流量）以及下游断面在t-△ t时刻的水位（流量），最后用式（15）、（16）得出下游断面水位（流量）。

2 相似涨落模型及算法

2.1 相似涨落法

从涨落差法的物理本质可看出，上、下游断面涨落差的比例因子kh及kq是水文预报的决定因素，但由于，除了Bu/Bd为常数外，对于非恒定流，其余各项皆为时间与空间的变量，传播时间也随洪水特性不同而变化，所以涨落差法的应用，面临着一个复杂的非线性问题，除了较大洪水且在干流上外，难以保证径流预报的精度。

文［1］和［2］分别将洪水特性和洪水过程作为预报的关键词，文［3］将相似性研究作为水文预报的基本方法之一。在此提出涨落差法：对于上游某一断面，在足够长的时段内，水文涨落过程与历史上同断面相同时段内若干个水文涨落过程相似，则由式（15）知，下游相应断面的水文涨落过程，也与历史上同一断面同一时段的若干个水文涨落过程相似，于是可由下游断面历史的若干个相似的水文涨落过程，“浮现”下游断面现时的水文涨落过程，从而进行现时的水文径流预报。

因为扩散波方程对于确定的边界条件，其解是唯一的。这样就可知在足够长的时段内上游给定断面水文过程完全一样的情况下，其“波动”过程及其对各参数的影响也是一样的，于是下游给定断面的水文过程就可确定。由此避开了转换系数kh、kq，水流传播时间τ，谢才系数c等的影响，简化了求解过程，提高了解的可靠性与精确性。

2.2 模型及算法

由2.2可得相似涨落差法的模型如图1，图中t0为下游断面预报时刻，τ为上、下游断面水流传播时刻，T为预报精度所需的水文过程时段。

图1 相似涨落差径流预报模型

由图1可得算法如下

取上游断面Su，径流数据集Nu；取下游断面Sd，径流数据集Nd；设Su到Sd的传播时间为τ。

如预报下游断面t0时刻的水位流量，在Su采取（t0-T-τ,t0-τ）时段的径流数据，T为采样时段长，△t=T/q为采样步长，j=1,2,……q为第次采样的时序值，得Su的（j=1,2,……q）涨落过程

采集Su历时T与（j=1,2,……q）相似的历史水文径流过程，记为j=1,2,……q），显然。

在（t0-T，t0）时段Sd处，采集Ru与对应的径流数据可得：

Sd的水文径流过程预报值为

相似测度可用几何相似，余弦相似，欧氏距离等；I的意义表集总计算，可以是取算术平均，加权平均，中值和最大相似度等。

3 实例

观音洲水电站位于珠江流域的北江下游广东省清远境内，电站装有4台贯流式灯泡机组，总装机容量44MW。观音洲水电站坝址上距飞来峡水库46.73km，下距石角水文站4.8km，集雨面积37783km2。根据飞来峡水库径流参数，预报观音洲水电站径流并用实测数据进行预报精度分析。

图2 2015年9月12日流量预测

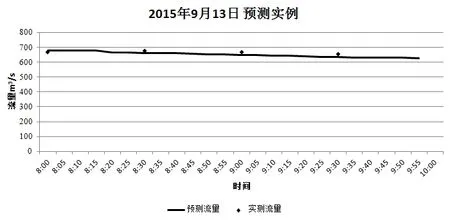
图3 2015年9月13日流量预测

图4 2015年10月10日流量预测

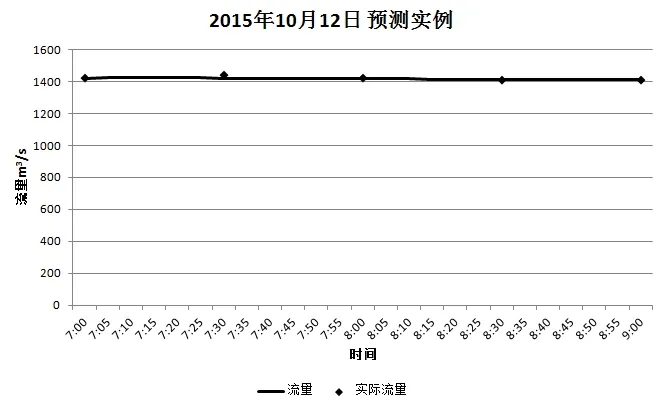
图5 2015年10月12日流量预测

由表1可见，其中误差5%合格率为88.24%，10%合格率为100%，预测精度较高。从流量变化趋势来看，预测的流量过程与实际的流量过程变化基本一致。目前，相似涨落差径流预报模型已成为观音洲水电站优化调度的基本依据。

4 结语

1） 相似涨落差法克服了传统涨落差法的非线性问题，可用于一般的径流预报。

表1 流量对比表

2） 相似涨落差法的实质是将历史数据进行挖掘，按相似原理再现历史，从而用经验进行预报，将相似性研究与经验相关、物理相关结合起来，属于水文预报研究的经典方法。

3） 相似涨落差法通过将一簇相似的水文过程集总而求解预报值，就消除了个别水文过程的偶然性，体现了由“混杂”导致“精确”的“大数据”原理，保证了预报精度的平稳性。

[1] 王光生，宁方贵，肖飞，姜涛.实用水文预报方法[M].北京：中国水利水电出版社，2008.

[2] 詹道江，叶守泽.工程水文学[M].北京：中国水利水电出版社，2000.

[3] 包为民.水文预报[M].北京：中国水利水电出版社，2006.

[4] 李兰.扩散波的时空反演与洪水实时预报技术[J].水文，1998，（06）.

[5]王光生，张建新，周砺.涨落差法原理再分析[J].水文，2009，（02）.

The Forecast Model of Similar Fluctuation Difference Runoff and its Application

WEI Xiao-yun1, HUANG Ding-bo1, ZHANG Kui-fei2, ZHENG Cheng-yao3
(1 Guangzhou Energy Science and Technology Co., Ltd., Guangzhou 510655, China; 2 Qingyuan Yuehua Power Co.,Ltd., Qingyuan 511500, China; 3 Guangdong Polytechnic of Water Resources and Electric Engineering, Guangzhou 510635, China)

As for the fluctuation difference model, the propagation time varies due to the flood characteristics;the up and down stream fluctuation difference of scale factor on kh and kq factors is more complicated; therefore,the fluctuation difference model, due to its nonlinear problem, affects the forecast accuracy. When hydrological observation data is sufficient, the historical fluctuation process similar to the section with current upstream section fluctuation process is identified. Through the downstream section of history of the corresponding fluctuation process,the runoff parameters of instant downstream section, such as water level and flux act, are identified. Thus, the similar fluctuation difference runoff forecast model is established, the application of which at Guanyinzhou Hydropower Station indicates a higher forecast accuracy of the model.

hydrological runoff forecast; diffusion wave; fluctuation difference method; hydrological similarity analysis

TM713

A

1672-2841（2016）02-0005-04

2016-05-03

卫小筠，女，助理工程师，从事流域水资源规划及水电站规划工作。