借力活动经历,凸显数学本质
2016-07-28冷蓉晖
冷蓉晖
[摘 要]数学的本质包括基本的数学概念、基本的数学思想方法、基本的思维方式、基本的数学探究。教师要借力数学活动,让学生经历活动探究,让学生在“做数学”中感受数学,从而凸显数学学科的本质。
[关键词]教学策略 数学本质 活动经历
[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068(2016)20-086
课程标准提出,要把握数学学科的本质,发展学生的数学能力。那么,在实践中如何才能有效把握数学本质?笔者认为,教师要精心设计有效的数学活动,让学生借力活动经历,充分经历活动过程,深刻理解基本概念,积累基本经验,由此实现从感性到理性的飞跃。
一、借力活动经历,理解基本概念
在小学数学教学中,数学基本概念的建构是一个循序渐进的过程,也是一个学生和教师积极参与的活动过程,教师要结合教学内容,给予学生充分的空间,借力层层深入的交流活动,带领学生经历观察、对比、思考、辨析、抽象和概括的过程,从而凸显数学本质。
例如,教学“方程的意义”时,我设计了循序渐进的分类活动:先出示天平,让学生列算式表示天平两边物体质量的大小关系,学生列出算式“(1)50+50=100;(2)x+50>100;(3)x+50=150;(4)x+50<200;(5)2x=200。”此时让学生对算式进行分类,学生根据等式的标准,将算式(1)(3)(5)分为一类,算式(2)(4)分为另一类;学生又根据含不含未知数的分类标准,将算式(2)(3)(4)(5)分为一类,算式(1)分为另一类。我抓住这个时机追问:“想一想,等式分类还可以怎么分?”学生根据含不含未知数这个标准,发现了关键所在:等式可以分为含有未知数的等式和不含未知数的等式。含有未知数的等式就叫做方程。那么,怎么用数字表征来表示方程呢?学生经过讨论后,认为类似ax+b=c这样的算式,就是方程。
以上教学,通过两次分类活动,学生经历了观察、对比、辨析,经历了数学概念的建构过程,经历了分类和建构的数学思想,凸显了数学教学的本质。
二、借力活动经历,培养基本技能
操作是思维的花朵。在小学数学教学中,教师通过设计操作活动,能够将操作、语言和思维有机结合,让学生经历丰富的活动体验,培养了学生的基本技能,发展了学生的数学能力。
例如,教学“圆的面积推导”时,我设计了操作探究的活动:如图1,让学生猜想圆的面积和半径是什么关系?学生提出:圆的面积比半径平方的4倍少一些。我再出示三个圆(如图2),让学生计算出每个圆的面积。学生通过数格子得到圆的面积之后,经过计算发现圆的面积是半径平方的三倍多一些。由此我提出问题:到底圆的面积是半径平方的多少倍?如何求出圆的面积?学生提出运用转化的方法,将圆拼成一个近似的平行四边形,并动手操作,将一个圆等分成16份,也有学生将其等分成32份、64份……通过操作发现,等分的份数越多拼成的图形就越接近长方形。此时我引导学生思考:拼成的长方形面积与圆的面积有什么关系?长方形的长、宽和圆的半径有什么关系?如何用长方形面积推导出圆的面积?由此,学生从猜想到计算、操作、推理,一步步深入探索圆的面积的推导过程,从而掌握了圆的面积计算公式。
学生充分经历操作和推理过程,在掌握圆的面积计算公式的同时,也积累了转化和极限思想方法,大大提升了基本技能,实现了方法性经验、策略性经验的有机结合。
三、借力活动经历,积累基本经验
要发展学生的基本活动经验,就要借力活动经历,引导学生发现数学知识之间的前后关联,从而积累基本的数学活动经验。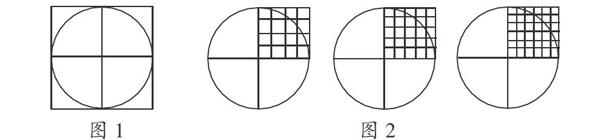
例如,教学“解决问题的策略:一一列举”时,我设计了反思回顾的活动:先出示“用22根1米长的木条,围成最大面积的花圃”这个问题,让学生说说在解决这个问题过程中的困惑,有学生提出在列举的过程中容易重复和遗漏,因此要按顺序列举;也有学生提出列举的方式可以是列表、文字、画图等;还有学生提出,列举时要根据问题的特点,灵活选择列举的方法。通过反思活动,学生的个体经验得到有效的补充和完善,对一一列举的策略有了深刻理解,积累了自身的基本活动经验。
总之,在小学数学教学中,教师是课堂活动的开发者和设计者,要结合具体的教学内容,组织有效的教学活动,借力活动经历,让学生在“做数学”中感受数学、思考数学,从而提升课堂效能,凸显数学本质。
(责编 童 夏)
