一个基于打靶法的大气污染源反演自适应算法
2016-07-27冯帆王自发唐晓
冯帆王自发唐晓
1中国科学院计算机网络信息中心/超级计算中心,北京1001902中国科学院大气物理研究所大气边界层物理和大气化学国家重点实验室,北京1000293中国科学院大学,北京100049
一个基于打靶法的大气污染源反演自适应算法
冯帆1, 2, 3王自发2唐晓2
1中国科学院计算机网络信息中心/超级计算中心,北京100190
2中国科学院大气物理研究所大气边界层物理和大气化学国家重点实验室,北京100029
3中国科学院大学,北京100049
摘 要污染源反演对大气污染预报及控制有重要意义。目前普遍采用的源反演统计方法存在对观测误差、源清单先验估计误差敏感等弱点。基于打靶法思想的各种算法以其精度高、程序简单、实用性强的特点被广泛应用于系统控制领域。本文提出的基于打靶法思想的大气污染源反演自适应算法在精度高、算法简明的基础上弥补了统计方法的不足:能处理源清单中的大误差、初值大误差、观测值在个别时间点的大误差;无需先验分布假设及误差估计。本文还以简单模型的理想试验为例,展示了该自适应算法的计算效果。
关键词打靶法 污染源 反演 自适应 系统控制
冯帆,王自发,唐晓. 2016. 一个基于打靶法的大气污染源反演自适应算法 [J]. 大气科学, 40 (4): 719−729. Feng Fan, Wang Zifa, Tang Xiao. 2016. Development of an adaptive algorithm based on the shooting method and its application in the problem of estimating air pollutant emissions [J]. Chinese Journal of Atmospheric Sciences (in Chinese), 40 (4): 719−729, doi:10.3878/j.issn.1006-9895.1505.15113.
1 引言
近年来,大气污染模式的研究得到了很大发展。污染排放源信息对模式至关重要。然而,建立污染源清单是一个具有较大不确定性的复杂过程,涉及对经济发展状况、人口密度、能源结构、工厂分布、交通流量、车型比例等多方面的调查研究。因此,根据模式的模拟值和监测站的污染物浓度观测值来反演污染源信息对大气污染预报及控制均有重要意义。
大气污染预报是已知原因求结果,属于正问题,即给定了微分方程和初、边值条件,求满足给定条件的解;而大气污染控制是由结果求原因,属于反问题,即排放源等参数作为未知量出现在微分方程中,我们需利用观测值等附加信息反求未知参数(刘峰等,2003;杨一帆和张凯山,2013)。多种方法已被应用于反演污染源,比如逆向轨迹法(蔡旭晖等,2002)、遗传算法(陈军明等,2002)、伴随方程法(刘峰等,2003;郭少冬等,2010)、四维变分法(Mendoza-Dominguez and Russell, 2001)、集合卡尔曼滤波法和集合卡尔曼平滑法(朱江和汪萍,2006;Tang et al., 2013)以及蒙特卡洛空间反演法(杨一帆和张凯山,2013)等。
目前,源反演普遍采用统计类方法,但其存在对观测误差、源清单先验估计误差敏感等弱点。而基于打靶法思想的算法恰好能弥补统计法的不足。打靶法思想的本质是将微分方程两时刻点间的演化问题转化为控制问题来求解,通过调整控制参量使观测时刻点的模拟值接近观测值。在源反演问题中,这个控制参量就是源排放速率。基于打靶法思想的各种算法以其精度高、程序简单、实用性强的特点被广泛应用于系统控制领域(向明华和刘云青,1990;屈香菊,1992;范慕辉和石铁君,1994;凌复华和李继跃,1988;Ning et al., 2004;吴文海等,2005;张洪波等,2008;齐笳羽等,2011)。
本文针对大气污染源反演问题提出一个基于打靶法思想的自适应算法。该算法在精度高、算法简明的基础上还弥补了许多统计方法的不足:能处理源清单中的大误差、初值大误差、观测值在个别时间点的大误差;无需先验分布假设及误差估计。本文还以简单模型的理想试验为例,给出了该自适应算法的计算效果。
2 源反演自适应算法设计
从污染物浓度观测值估计污染物排放速率可作为系统控制问题进行考虑。其中,污染物排放速率为控制变量。关于打靶法思想介绍,见附录A。基于打靶法的思路,我们可以将观测值作为靶子,设法寻找使模拟值与观测值的距离小于容忍度的排放速率。
该算法设计的困难主要来自以下两方面:第一,直观上,当模拟值大于观测值时,我们需减小排放速率;当模拟值小于观测值时,我们需增大排放速率。那么如何增减能使射击次数尽量小且程序简明;第二,除了源清单的误差,实际中还不可避免地会遇到初值误差、观测误差。当这些误差较大时,算法能否及时纠错,使模拟值尽快主动回到正常位置(而不是被动地等待长时间模式预热,即Spin Up)。增强算法的健壮性,使算法具有纠错功能的必要性说明见附录B。
因此,采用何种打靶策略能够立刻对上述可能出现的大误差进行纠错并且较为快速、准确地进行源反演是本算法设计要解决的核心问题。这里,进行源反演可利用的唯一信息是误差(Err)=模拟值-观测值。如何利用误差 Err对排放速率进行高效校正是十分重要的。判定何时需要对大误差及时纠错以及如何纠错也是要解决的关键问题。
2.1 源反演的打靶问题描述
若不考虑模式误差,大气污染物浓度在某一空间点上的抽象模型可以表示为
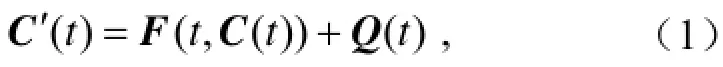
其中,C是污染物浓度的向量(其分量表示不同污染物种的浓度);是污染源排放速率的向量;算子F表示污染物的输送、化学过程。
假定在t1, ..., tk时刻有污染物的浓度观测向量Y1, ..., Yk,则在时间段[ti, ti+1]i=0, 1, …, k−1的污染物浓度演化过程可视为打靶问题:在该时间段上控制Q,使得

其中,Tol为设定的允许误差界限。于是,源反演问题转化成了分时间段的打靶问题。Q 在每个时间段上为常值向量。
2.2 源反演的打靶算法设计
基于上面的叙述和分析,我们在本节给出各时间段[ti, ti+1]上的自适应算法流程。
在每个时间段[ti, ti+1]上,算法分为三大步:初始化、若干次射击和保存本时间段的结果。若干次射击又分成4小步,其中步骤(c)(用的当前值在[ti, ti+1]上解初值问题)即射击。
在每次射击后更新s维误差向量Err=C (ti+1;(其中C只提取与Y相同的物种分量),为下一次射击前校正向量作准备[见2.2.1节中步骤(d.1)]。
注意到只有通过有效的观测信息,我们才有可能得到有效的源反演值。当初值或观测值在个别时间点存在大误差时,反演信息必然无效。由于观测值在若干个时间点可能存在大误差,这使得系统在自然状态下会经历若干个Spin Up,导致反演信息在Spin Up期间均无效。因此,主动采取措施自动纠错、增强算法的健壮性、使污染物浓度和源反演结果立刻回到正常位置是十分必要的(纠错的必要性图例说明见附录B)。
当初值或观测值在个别时间点存在大误差时,我们的算法恰恰能自动纠错,使污染物浓度和源反演结果迅速回到正常位置。这就大大增强了算法的健壮性,从观测值中尽可能多地反演出有效源排放速率[见2.2.1节中步骤(d.2)]。实际上,为了得到最终的有效信息,我们将对结果进行后处理:去掉纠错阶段的源排放速率(见本文数值试验中图1e–f’)。
2.2.1 算法
(2)当s维向量|Err|存在分量大于允许误差界限Tol且ShootingCount小于MaxShooting(最大射击次数)时,步骤分为:(a)ShootingCount= ShootingCount+1;(b)用设定的经验值初始化的当前值在[ti, ti+1]上解初值问题,得到各物种浓度计算方法如下:
For j = 1到s
(d.2)用Err(j) 更新Q (j):[公式(3)为核心,其他均为了增强算法健壮性、为了纠错而设计]为正:
否则
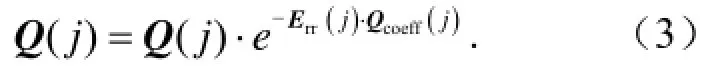
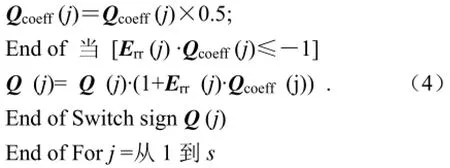
(3)保存本时间段[ti, ti+1]的计算结果,为下一时间段作准备;保存经过若干次射击最终接受的和用给下一时间段赋初值。
2.2.2 算法须注意问题
(1)源清单中各物种的排放速率为非负值。在运行此算法之前,我们需要对源清单进行预处理:如果某物种有观测值且该物种在源清单中某时刻的排放速率为零,则用一个小的正数代替零。这样才能使步骤(d.2)的更新公式起作用。
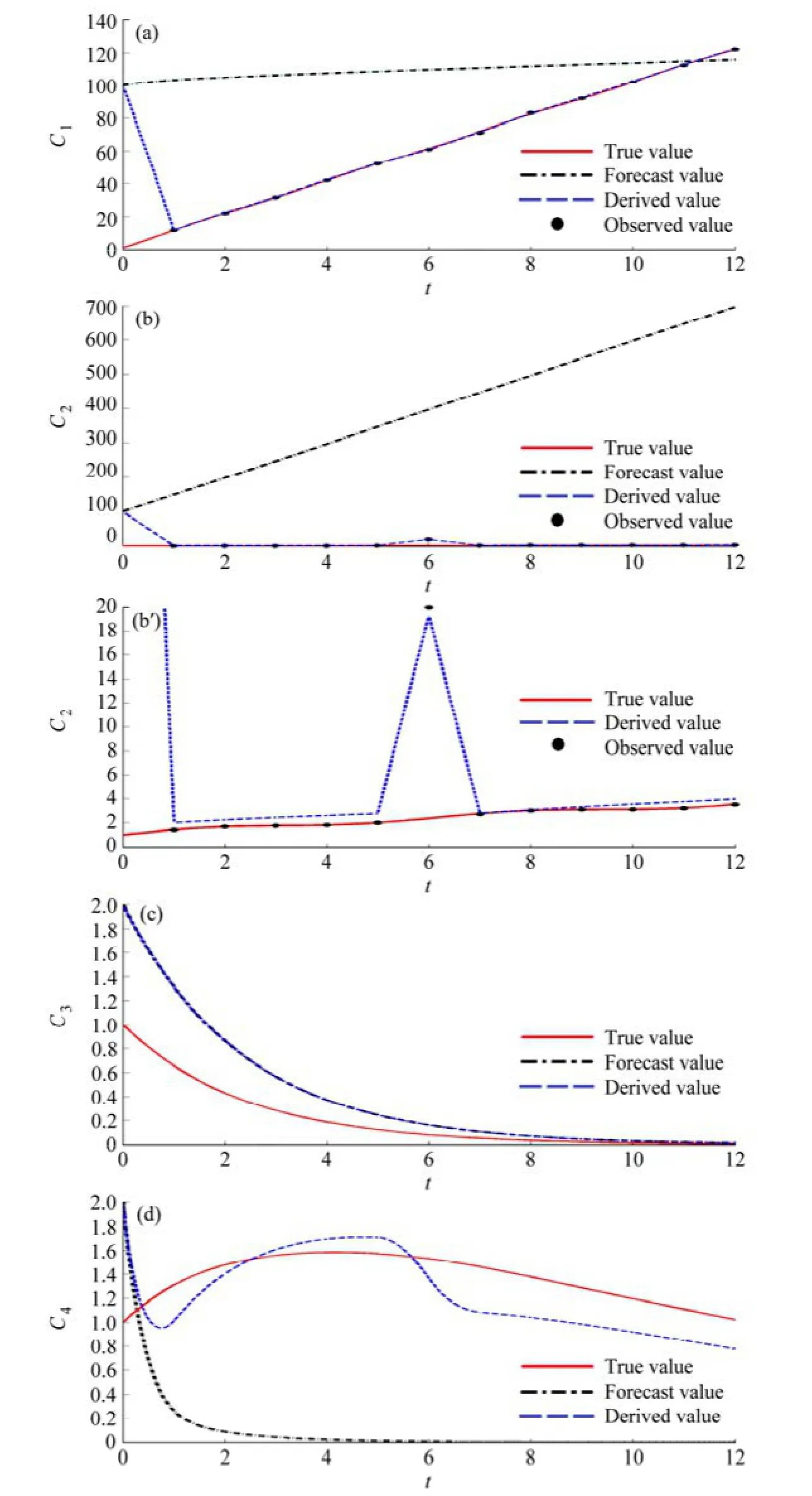
图1 试验1的结果:(a)浓度C1;(b)浓度C2;(b’)为(b)C2的局部放大;(c)浓度C3;(d)浓度C4;(e)Q1源排放速率;(e’)为(e)Q1去掉纠错阶段;(f)Q2源排放速率;(f’)为(f)Q2去掉纠错阶段Fig. 1 Results of Experiment 1: (a) Concentration C1, (b) concentration C2, (b’) partial enlargement of (b), (c) concentration of C3, (d) concentration of C4, (e) emissions rate of Q1, (e’) panel (e) without error correction phase, (f) emissions rate of Q2, (f’) panel (f) without error correction phase
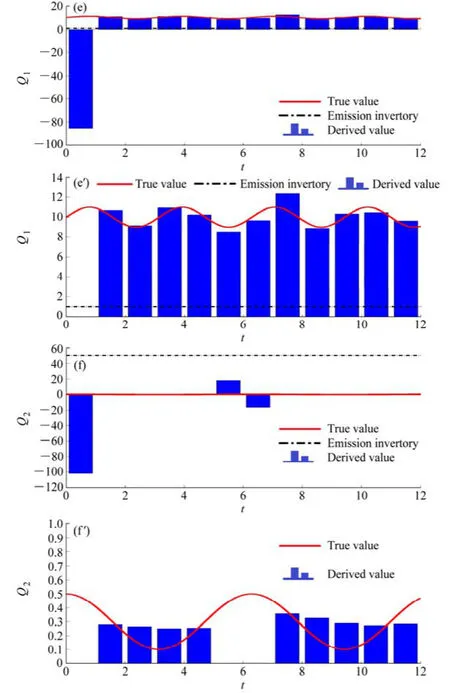
图1 (续)Fig. 1 (Continued)
(2)在试验中,我们对各物种使用了相同的允许误差界限 Tol。实际上,为了进一步减小射击次数,不同的物种可以使用不同的 Tol:值域范围大的物种取值相对大,值域范围小的物种取值相对小。Tol 不宜过小。
(3)2.2.1节中步骤(d.2)的 CheckCritical 为设定的较小正值。当源排放速率已经非常小时,若仍有Err (j)>Tol,那么我们决定使用负值纠错。实际上,这负值在后处理中作为纠错阶段的源排放速率将被去掉。(见图1e–f’)
3 简单模型的数值试验
在本节中,我们采用下面描述空气质量的简单无量纲模型进行试验:
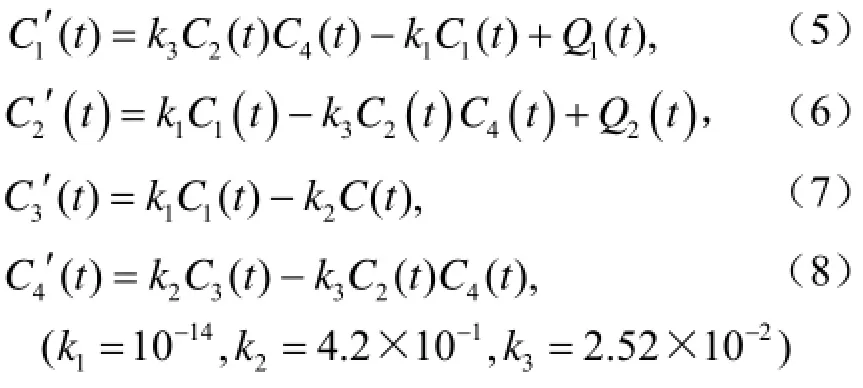
其中,Ci是第i个物种的浓度,是随时间变化的污染源排放速率。试验在tÎ[0,12]上进行,共3个试验,具体设置见表1。在试验中,我们假设真实初始浓度在试验1、试验2中,假设真实排放速率在试验3中,假设真实排放速率在我们的试验中不考虑模式误差。试验各时间段的射击次数见表2。
在本文的数值试验中,经验参量 Qcoeff第一个分量对应Q1,第二个分量对应Q2。源清单的排放速率均为
试验1的目的是检验本算法对污染物浓度的反演效果和污染源反演能力。从试验1的结果我们看到:本算法可使用较少射击次数反演源(表2和表3),并且能处理源清单中的大误差、初值大误差、观测值在个别时间点的大误差(图1;图1b’在时刻6的观测值存在大误差)。反演后,没有用观测值反演的物种浓度也有可能得到改善(图1d)。在源排放速率变化很小的情况下,我们从反演结果仍能够看到源变化趋势(图1f’)。另外,试验1与附录B展示了负值纠错功能的必要性。
试验2除了观测时间间隔不同,其他均与试验1相同(表1)。对比试验1与试验2,其他设置不变,只在时间上加密观测数据不一定得到更准确的反演源(图2),而且射击次数可能会明显增加(表2)。
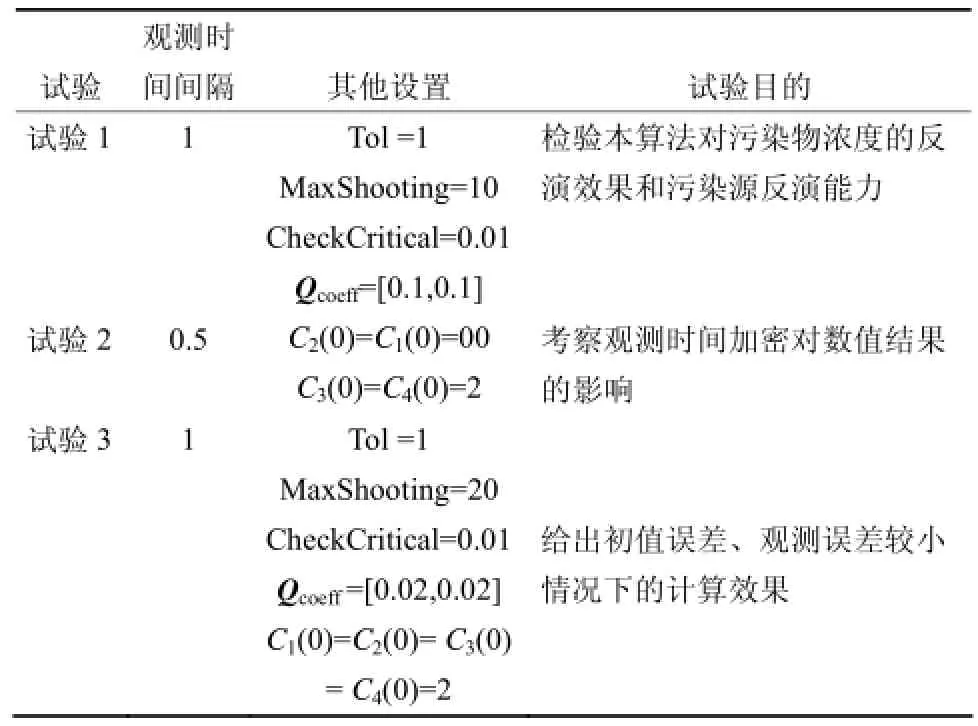
表1 试验列表Table 1 The detailed setup of the experiments
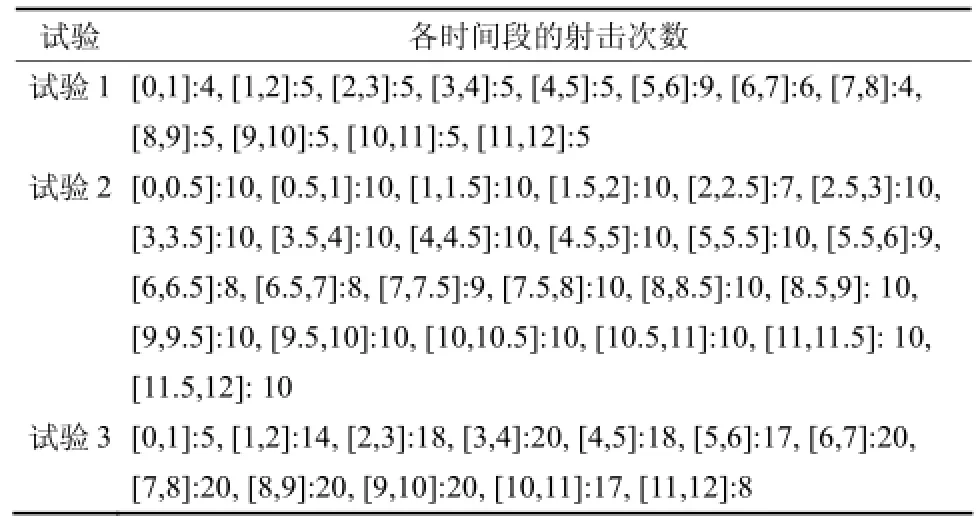
表2 射击次数列表Table 2 Shooting times over each time span

表3 试验1的源反演过程Table 3 The shooting process of emission in Experiment 1
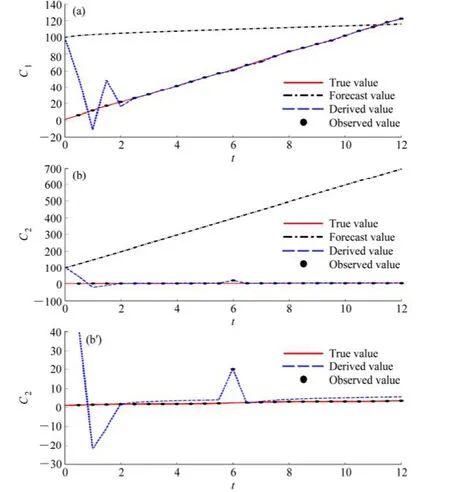
图2 试验2的结果:(a)浓度C1;(b)浓度C2;(b’)为(b)C1的局部放大;(c)Q1源排放速率;(c’)为(c)Q1去掉纠错阶段;(d)Q2源排放速率;(d’)为(d)Q2去掉纠错阶段Fig. 2 Results of Experiment 2: (a) Concentration C1, (b) concentration of C2, (b’) partial enlargement of (b), (c) emissions rate of Q1, (c’) panel (c) without error correction phase, (d) emissions rate of Q2, (d’) panel (d) without error correction phase
试验3给出了在初值、观测值误差不太大情况下的算法效果。反演后的源较好地与真值吻合(图3)。
4 小结和讨论
污染源反演问题常作为统计估计问题处理。比如,四维变分法、集合卡尔曼滤波是人们常用于反演的统计方法。四维变分法本质上是使目标函数极小化的泛函问题。集合卡尔曼滤波是一种用蒙特卡罗短期集合预报来估计预报误差协方差的四维变分方法。集合卡尔曼滤波无需模式反向积分,无需预报模式的切线性模式和伴随模式,因此与四维变分法相比,更容易实现、可移植性强。然而,四维变分、集合卡尔曼滤波等统计方法存在下面几个弱点:先验分布的高斯假设;线性的分析方程在模式为强非线性时,对结果造成不利影响;对观测误差较敏感;污染源排放的先验误差估计对反演结果有较大影响(朱江等,2006)。
本文提出的基于打靶法思想的大气污染源反演自适应算法本质上是系统控制问题,与统计量无关,且计算过程中用到的主要信息为观测值。只要观测值本身合理、有效,就可以反演出可信的源排放速率。如果我们具备可靠的观测误差信息,则可利用该信息先对观测数据作前处理校正,然后再应用本文设计的打靶算法进行源反演。
该基于打靶法思想的大气污染源反演算法弥补了四维变分、集合卡尔曼滤波等统计方法的不足,具有如下特点:(1)能处理源清单中的大误差、初值大误差、观测值在个别时间点的大误差;(2)无需先验分布假设及误差估计。在实际中,对污染源进行反演是一个很复杂的问题。污染源与观测站点的空间分布不均匀性、可观测的物种少于需要反演的污染源物种等局限性会使反演结果不唯一。在今后的工作中,我们会考虑通过有效地增加约束条件或信息来处理这一问题。
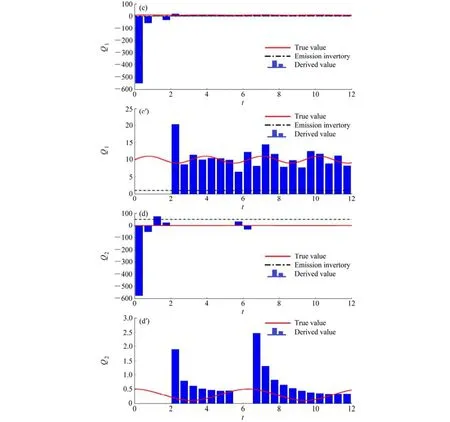
图2 (续)Fig. 2 (Continued)
气象场误差、模式分辨率误差、化学机制误差等因素均可造成模拟与观测不一致。如果忽略这些模式误差、仅通过调整排放源来减小模拟和观测之间的不一致,那么源反演结果将会出现偏差。集合卡尔曼滤波/平滑考虑了各种误差对源反演的影响(Tang et al., 2013)。如何将集合卡尔曼滤波/平滑与本文提出的基于打靶法思想的自适应算法结合起来解决源反演问题也是我们今后将要探讨的。
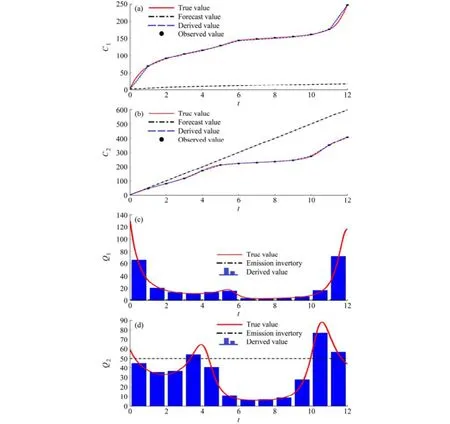
图3 试验3的结果:(a)浓度C1;(b) 浓度C2;(c)Q1源排放速率;(d)Q2源排放速率Fig. 3 Results of Experiment 2: (a) Concentration C1, (b) concentration C2, (c) emissions rate of Q1, (d) emissions rate of Q2
致谢 感谢中国科学院大气物理研究所朱江研究员及审稿专家们对本文提出的宝贵意见。
参考文献(References)
蔡旭晖, 邵敏, 苏芳. 2002. 甲烷排放源逆向轨迹反演模式研究 [J]. 环境科学, 23 (5): 19–24. Cai Xuhui, Shao Min, Su Fang. 2002. A backward trajectory inversion model for methane emission over Beijing area [J]. Environ. Sci. (in Chinese), 23 (5): 19–24, doi:10.3321/j.issn: 0250-3301.2002.05.004.
陈军明, 徐大海, 朱蓉. 2002. 遗传算法在点源扩散浓度反演排放源强中的应用 [J]. 气象, 28 (9): 12–16. Chen Junming, Xu Dahai, Zhu Rong. 2002. Application of genetic algorithms to point-source inversion [J]. Meteor. Mon. (in Chinese), 28 (9): 12–16, doi:10.3969/j.issn.1000-0526.2002.09.003.
范慕辉, 石铁君. 1994. 打靶法在力法解超静定梁中的应用 [J]. 河北工学院学报, 23 (4): 32–37. Fan Muhui, Shi Tiejun. 1994. The shooting method’s application in solving statically indeterminate beams [J]. J. Hebei Inst. Technol. (in Chinese), 23 (4): 32–37.
郭少冬, 杨锐, 苏国锋, 等. 2010. 基于伴随方程和 MCMC方法的室内污染源反演模型研究 [J]. 应用基础与工程科学学报, 18 (4): 695–704. Guo Shaodong, Yang Rui, Su Guofeng, et al. 2010. Investigation of the inversion modeling for indoor contaminant source based on the adjoint equation and MCMC method [J]. J. Basic Sci. Engin. (in Chinese), 18 (4):695–704, doi:10.3969/j.issn.1005-0930.2010.04.017.
凌复华, 李继跃. 1988. 打靶法在常微分方程边界层型奇异摄动问题中的应用 [J]. 应用数学和力学, 9 (7): 609–615. Ling Fuhua, Li Jiyue. 1988. Shooting method in singular perturbation problem of ordinary differential equations with boundary layers [J]. Applied Mathematics and Mechanics (in Chinese), 9 (7): 609–615.
刘峰, 胡非, 王锷一. 2003. 用伴随方程研究空气污染的优化控制 [J].环境科学学报, 23 (4): 472–475. Liu Feng, Hu Fei, Wang Eyi. 2003. Study on optimal control of air pollution using adjoint equation [J]. Acta Scientiae Circumstantiae (in Chinese), 23 (4): 472–475, doi:10.3321/j. issn:0253–2468.2003.04.012.
Mendoza-Dominguez A, Russell A G. 2001. Estimation of emission adjustments from the application of four-dimensional data assimilation to photochemical air quality modeling [J]. Atmos. Environ., 35 (16): 2879–2894, doi:10.1016/S1352-2310(01)00084-X.
Ning Jiping, Han Qun, Chen Zhiqiang, et al. 2004. A powerful simple shooting method for designing multi-pumped fibre Raman amplifiers [J]. Chin. Phys. Lett., 21 (11): 2184–2187, doi:10.1088/0256-307X/21/11/ 030.
齐笳羽, 祝金川, 李成仁, 等. 2011. 打靶法实现Lorenz-Haken激光混沌的周期和稳态控制 [J]. 半导体光电, 32 (1): 132–134. Qi Jiayu, Zhu Jinchuan, Li Chengren, et al. 2011. Realization of periods and steadystate control for Lorenz-Haken laser chaos with shooting method [J]. Semiconductor Optoelectronics (in Chinese), 32 (1): 132–134.
屈香菊. 1992. 直接多重打靶法在轨迹优化方面的应用 [J]. 飞行力学, 10 (1): 13–21, 39. Qu Xiangju. 1992. The application of the multiple shooting algorithm to trajectory optimization [J]. Flight Dynamics (in Chinese), 10 (1): 13–21, 39.
Tang Xiao, Zhu Jiang, Wang Zifa, et al. 2013. Inversion of CO emissions over Beijing and its surrounding areas with ensemble Kalman filter [J]. Atmos. Environ., 81: 676–686, doi:10.1016/j.atmosenv.2013.08.051.
吴文海, 周志刚, 韩强, 等. 2005. 基于打靶法的战机攻击导引方法研究[J]. 飞机设计, (1): 47–51. Wu Wenhai, Zhou Zhigang, Han Qiang, et al. 2005. Study on attack trajectory of pursuiting fighter based on shooting method [J]. Aircraft Design (in Chinese), (1): 47–51, 10.3969/ j.issn.1673-4599.2005.01.011.
向明华, 刘云青. 1990. 边值打靶法的改进与应用 [J]. 哈尔滨船舶工程学院学报, 11 (4): 449–456. Xiang Minghua, Liu Yunqing. 1990. Modification and application of the multiple shooting method [J]. Journal of Harbin Shipbuilding Engineering Institute (in Chinese), 11 (4): 449–456.
杨一帆, 张凯山. 2013. 突发型大气污染源位置识别反演问题的数值模拟 [J]. 环境科学学报, 33 (9): 2388–2394. Yang Yifan, Zhang Kaishan. 2013. Numerical simulation on source identification of accidentally occurring air pollution [J]. Acta Scientiae Circumstantiae (in Chinese), 33 (9): 2388–2394.
张洪波, 郑伟, 汤国建. 2008. 采用打靶法设计考虑地球扁率的机动轨道 [J]. 宇航学报, 29 (4): 1177–1181. Zhang Hongbo, Zheng Wei, Tang Guojian. 2008. Maneuver trajectory design with J2correction based on shooting procedure [J]. Journal of Astronautics (in Chinese), 29 (4): 1177–1181, doi:10.3873/j.issn.1000-1328.2008.04.017.
朱江, 汪萍. 2006. 集合卡尔曼平滑和集合卡尔曼滤波在污染源反演中的应用 [J]. 大气科学, 30 (5): 871–882. Zhu Jiang, Wang Ping. 2006. Ensemble Kalman smoother and ensemble Kalman filter approaches to the joint air quality state and emission estimation problem [J]. Chinese Journal of Atmospheric Sciences (in Chinese), 30 (5): 871–882, doi:10.3878/j.issn.1006-9895.2006.05.16.
附录A 打靶法基本思想简介
在科学与工程计算中,会经常遇到边值问题。打靶法源于将边值问题化为初值问题来解。对于二阶常微分方程边值问题:
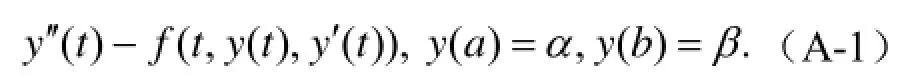
可以化为初值问题来求解:
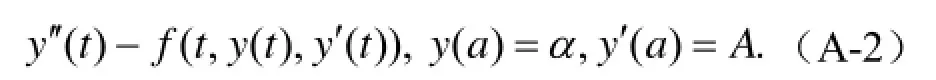
我们设法确定 A的值,使得初值问题[公式(A-2)]的解(;)y t A在tb=的值(;)y b A满足
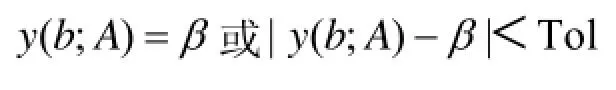
其中,Tol为我们允许的误差界限。
于是,我们得到了边值问题[公式(A-1)]的近似解(;)y t A。
显然,图A-1打靶法思想是系统控制问题:A为控制变量,b为t = b时的系统观测值,通过调节A使模拟值(;)y b A接近观测值b。
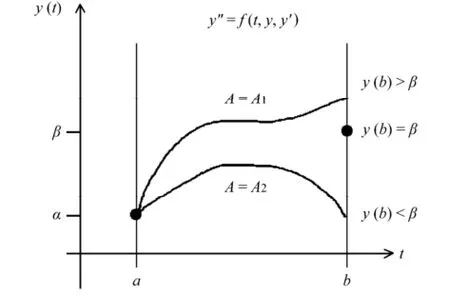
图A-1 打靶法示意图:将边值问题化为初值问题来解Fig. A-1 Sketch of the shooting method: Transforming a boundary value problem into an initial value problem
附录B 算法中纠错功能的必要性——增强健壮性
去掉负值纠错功能,如图所示,C1的浓度值从时刻10开始才逐渐Spin Up到正常位置(图B-1a);C2的浓度值需要更长的时间才能 Spin Up到正常位置(图B-1b);Q1源排放速率从时刻11开始才逐渐提供有效信息(图B-1c)。Q2源排放速率需要更长的时间才能提供有效信息(时刻12以前均为无效信息)。
对比图1与图B-1,在初值或观测值误差较大的情况下,去掉负值纠错功能的算法提供的有效源反演信息很少。因此,考虑负值纠错功能使得算法健壮性大大增强。
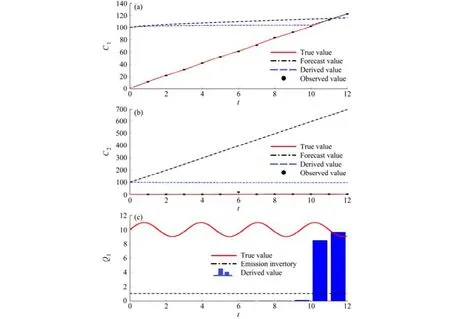
图B-1 试验1去掉负值纠错功能的结果:(a)浓度C1;(b)浓度C2;(c)Q1源排放速率Fig. B-1 The results of Experiment 1 without error correction function: (a) Concentration C1; (b) concentration C2; (c) emissions rate of Q1
资助项目 中国科学院战略性先导灰霾专项XDB05030200
Funded by Strategic Priority Research Program (B) of the Chinese Academy of Sciences (Grant XDB05030200)
文章编号1006-9895(2016)04-0719-11 中图分类号 X11 P409
文献标识码A
doi:10.3878/j.issn.1006-9895.1505.15113
收稿日期2015-01-19;网络预出版日期 2015-09-21
作者简介冯帆,女,1981年出生,博士研究生,主要从事应用数学建模及算法研究。E-mail: feng_fan_100@hotmail.com
Development of an Adaptive Algorithm Based on the Shooting Method and Its Application in the Problem of Estimating Air Pollutant Emissions
FENG Fan1, 2, 3, WANG Zifa2, and TANG Xiao2
1 Supercomputing Center, Computer Network Information Center, Chinese Academy of Sciences, Beijing 100190
2 State Key Laboratory of Atmospheric Boundary Layer Physics and Atmospheric Chemistry, Institute of Atmospheric Physics, Chinese Academy of Sciences, Beijing 100029
3 University of Chinese Academy of Sciences, Beijing 100049
AbstractThe inversion of pollutant emissions is important in air pollution prediction and control. The statistical methods generally adopted possess weaknesses, such as sensitivity for observation error and prior estimation of emissions. Given their simplicity, high precision, and practicality, algorithms based on the shooting method are widely used in the field of systems control. In this paper, we derive a shooting method–based adaptive algorithm to estimate air pollutant emissions. Besides its high precision and simple procedure, this adaptive algorithm compensates for the weaknesses of statistical methods. It is able to deal with the large level of error in the emissions inventory, initial conditions, and observations; a prior distribution assumption and error estimation are not required. Simulations of a simple system are presented to illustrate the effectiveness of this adaptive algorithm.
KeywordsShooting method, Pollutant emissions, Inversion, Adaptive algorithm, Systems control
