基于线阵CCD的波流调制效应水槽实验研究*
2016-07-27杜文超王小青陈鹏真
杜文超,王小青,刘 利,陈鹏真
(1.海军装备部驻天津军事代表局,北京 100070;2.中国科学院 电子学研究所,北京 100190;3.微波成像国家重点实验室,北京 100190)
基于线阵CCD的波流调制效应水槽实验研究*
杜文超1,王小青2,3*,刘利2,3,陈鹏真2,3
(1.海军装备部驻天津军事代表局,北京 100070;2.中国科学院 电子学研究所,北京 100190;3.微波成像国家重点实验室,北京 100190)
摘要:波流调制效应是指海面非均匀流场产生的挤压和拉伸,进而导致海面局部小尺度波浪谱发生增强或削弱的效应,它是内波、海底地形、海洋锋面等多种海洋现象能被SAR等微波遥感手段观测到的重要物理机制。波流调制效应非常复杂,与海面风速、波浪谱、流场等因素都有关系,直接在海面上开展精确的实验测量非常困难,且重复性差,而在水槽内可以实现较为精确的测量和重复性。本文给出了在水槽实验室内基于线阵CCD同步获取水面波浪谱和流场的测量方法,克服了传统的传感器无法同步获取波浪谱和水面流场的缺点,并在分层流水槽内对孤立内波产生的非均匀流场的波流调制效应进行了观测。研究结果表明基于线阵CCD的测量方法是研究波流调制效应的有效手段,尤其适合对厘米/毫米波段小尺度波浪谱的波流调制效应的研究。此外,在波长小于3 cm时波流调制模型的松弛率与经典模型的预测结果有较大出入,需要进一步深入研究。
关键词:线阵CCD;水槽实验;扰动流场;松弛率
波流调制效应是由于海面非均匀流场的拉伸和挤压效应形成的海面局部的小尺度波浪谱发生增强或削弱的效应。像SAR、散射计等微波遥感手段在进行海洋遥感时,其散射强度取决于海面粗糙度,当入射角为20°~70°中等入射角范围内时,对海面散射起决定性作用的是海面上波长量级与电磁波量级相当的小尺度波浪谱,这也就是著名的Bragg散射效应[1]。当波流调制改变海面粗糙度后就会在微波遥感图像上显现出流场的纹理特征,波流调制效应在很多海洋现象的微波遥感机理中都扮演了重要的角色,例如海洋锋面、海底地形、内波[2]等。因此,研究波流调制效应对海洋遥感机理的研究有非常重要的意义。
目前,国际上对波流调制效应的研究主要是针对波长大于3 cm的小尺度波浪谱(对应X波段以下的雷达波段的Bragg波)。由于比X波段更高的波段(例如Ku波段、Ka波段)目前在海洋遥感上还没有大量的应用,对于波长小于3 cm的小尺度波谱的波流调制效应目前还没有充分的研究,在零星的研究中有一些学者指出用传统的波流调制模型解释Ku、Ka波段海洋SAR图像时吻合度不高,但是相关机理和模型学界还没有统一的认识[3]。随着Ku、Ka等高波段雷达技术的发展,尤其是大功率发射机等关键器件的发展,这些高波段雷达在不久的将来必然会在海洋遥感上发挥重要的作用,因此开展厘米和毫米波段小尺度波的波浪调制效应的研究有重要的意义。
由于在海上对厘米和毫米波段的小尺度波浪谱的精确测量非常困难,重复性也很难得到保障。而水槽实验室容易实现小尺度波谱的高精度测量,另外也可以实现很好的重复性,因此实验室水槽是研究小尺度波浪谱的波流调制效应的理想实验环境。研究波流调制效应的另一个问题是观测传感器。当出现波流调制效应时水面流场和波浪谱都会同时发生变化,因此实验所需的传感器必须能同步获取水面的流场和波浪谱的实时变化。传统的表面高精度流场测量方法主要是基于PIV(Particle Image Velocimetry,粒子图像测速)方法进行测量,这种方法是在水面散布示踪粒子,根据示踪粒子的移动测量流场。但在存在表面波浪环境下,风生波会对示踪粒子的运动产生严重的影响。用PIV方法直接测得的是波浪的振动速度与表面流场的叠加结果,难以将二者区分开来。因此,目前传统的传感器无法同步获取表面波浪谱和表面流场变化,这给波流调制效应的研究带来的很大的困难。目前对于小尺度波的测量手段包括浪高仪、颜色编码、光强编码、电感耦合器件(Charged-coupled Device, CCD)线阵等几种方法,其中基于线阵CCD的波浪测量方法因为其扫描频率高(可以达到上千Hz),非常适合振动频率较高的小尺度波谱测量。
本文一方面利用线阵CCD对波浪谱的测量,另一方面利用波浪相速度与水面流场的关系从CCD信号数据中反演水面流场变化,这样就可以同步获取波流调制效应中最关键的两个物理量——波浪谱和流场,这就使得对波流调制效应的高精度观测成为可能。本文的水槽实验是在解放军理工大学的分层流水槽中开展的,通过激发内孤立波,在表面形成不均匀流场,对表面的风生波浪进行调制,形成波流调制效应,通过6台线阵CCD进行同步观测,实现了对厘米和毫米量级的小尺度波浪谱波流调制效应的观测。
1基于线阵CCD的表面波谱测量方法
CCD是一种半导体器件,能够感应光强并转换成数字信号。线阵CCD不同于普通的面阵CCD,其感光单元只有一排,因此可以实现很高的刷新率,且单个像素的测量精度和分辨率较高,广泛地应用在产品尺寸测量和分类等领域。
在水槽实验光学测量系统中应用线阵CCD除了可以获得比普通面阵CCD更高的分辨率外,还可以进行较长时间的高速连续测量,数据量比面扫描相机要少的多。这对水槽实验的开展以及实验数据的处理都十分有利。
基于线阵CCD的波浪测量方法是近年来国际上出现的一种高精度、高速的空时二维测量方法。Titov等学者已将其成功应用于实际海上及水槽实验中[4-5]。其基本原理如图1所示,光源经过遮光板后变为漫射光,水面反射光强取决于水面倾角(波斜率)。通过图像灰度标定,可以确定线阵CCD扫描区域内每个测量点的图像灰度与斜率的映射关系。
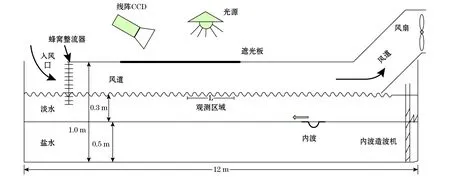
图1 实验装置侧视示意图Fig.1 Schematic diagram of the experiment setup
实验中使用6台线阵CCD相机,均垂直于波浪传播方向布设,如图2所示。所有CCD相机的参数一致,且相互之间的成像范围不重叠。

图2 实验中线阵CCD装置图Fig.2 CCD linear array in the experiment
图3是实验中获得的测量区域内4个位置点的图像灰度与波斜率映射曲线。在得到每个测量点的图像灰度-斜率映射关系后,根据线阵CCD成像结果便可计算出表面波斜率。在设计光源时要保证图像灰度与斜率的映射曲线是单调的一一映射关系,这样就获取图像强度后直接根据查表法将图像灰度转换为斜率。由于图像灰度与斜率的映射关系标定涉及到较为复杂的光学计算,超出了本文的范围,本文不对此进行详细介绍。

图3 线阵CCD测量区域内不同测量点的图像灰度-斜率映射关系曲线Fig.3 Mapping curves of image intensity vs.wave slope for selected measurement points
将线阵CCD每次扫描结果按时间累积之后得到RTI(Range-Time-Intensity,距离-时间-强度)图像。实验中得到的RTI图像数据如图4所示。实验中线阵CCD的有效扫描长度约为23 cm,扫描点数为600,空间分辨率为0.38 mm,时间分辨率为1/300 s。
图4为5.2和6.5 m/s两种典型风速(本文中所提的风速均为经过摩擦风速等效转换后的10 m高度处风速)下线阵CCD获取的光学二维图像和经过光强-斜率转换后的表面波斜率分布。图中距离方向(竖轴)是沿着波传播的方向。
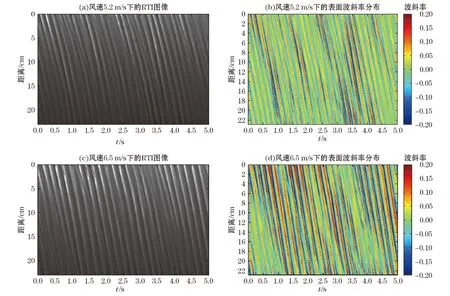
图4 5.2和6.5 m·s-1风速下的RTI和表面波斜率图像Fig.4 Images of RTI and slope at wind speeds of 5.2 and 6.5 m·s-1
图5是在风速5.2 m/s情况下,用1 s内的波斜率数据计算的表面波斜率二维频谱,其中黑色曲线是经典波浪频散关系。从图中可以看出,表面波频率成分集中在理论频散曲线附近。理论频散关系为
(1)
式中,k为波浪波数;ρ为水体密度;T=7.4e-2N/m,为表面张力系数;g为重力加速度。可用频域二维滤波器对斜率二维频谱滤波,滤波范围可自适应地选择为其谱宽。因此,可以对表面波斜率数据进行二维频域滤波,将波谱集中区域之外的信号滤除。经过滤波后的表面波斜率分布如图6所示,与图4(b)相比,斜率分布更加清晰。
通过CCD直接测量的是斜率,斜率与波高的关系为
(2)
式中,s(x,t),h(x,t)分别为斜率和波高;x为空间位置;t为时间。
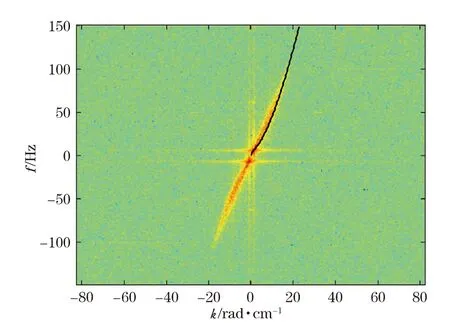
图5 表面波斜率二维频谱Fig.5 2-D spectrum of surface wave slope
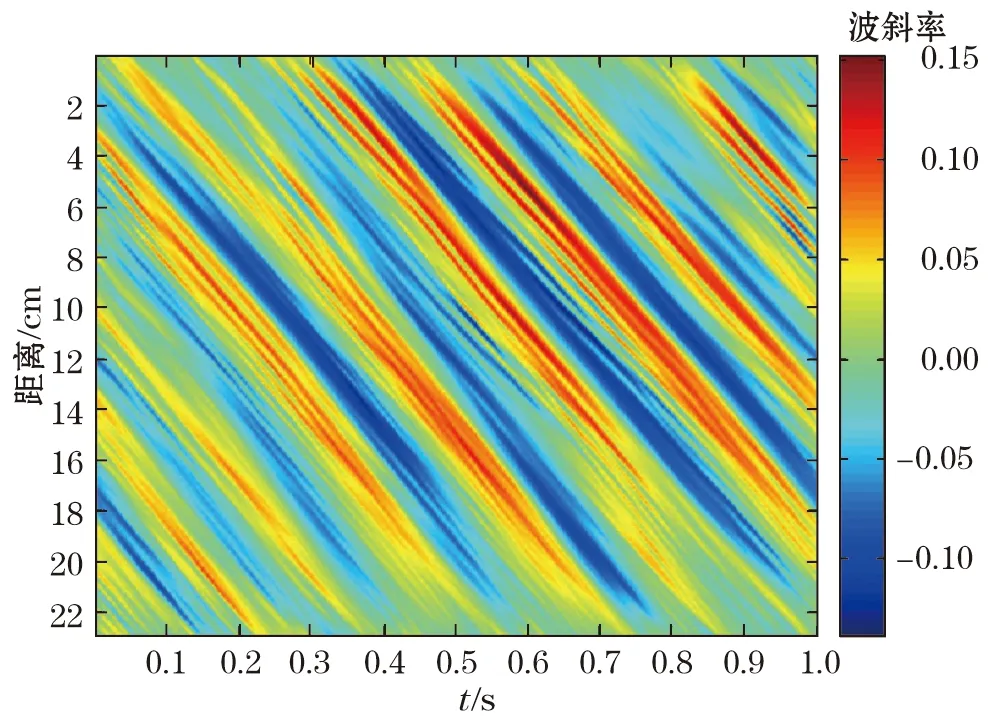
图6 滤波后的波斜率分布Fig.6 Filtered surface wave slope
采用傅里叶分析法可以简洁地从斜率计算波高,对式(2)两边进行空间维傅里叶变换,再稍加变换可得
(3)
式中,S(k,t),H(k,t)分别为斜率和波高空间维傅里叶变换;k为波数。
2基于线阵CCD的表面扰动流场测量方法
对风浪环境下的流场进行测量是研究波流相互作用机理的核心步骤。传统PIV方法在风浪环境下直接测得的表面速度是波浪的轨道速度与表面弱流场的叠加结果,并且难以将二者区分开来。
在水槽实验中,利用线阵CCD可以获得波浪相位的连续变化,根据表面波浪的相位变化获得表面波的相速度,据相速度的变化来计算表面扰动流场的速度。
在风浪环境下,表面波的相速度可以表示为[6]
(4)
式中,c0为表面波的本征相速度;ud为风引起的风生流场速度;uc即为所要测量的表面扰动流场速度。根据经典的波浪色散关系(式(1)),波浪的本征相速度为
(5)
式中,g为重力加速度;T为水面张力系数;ρ为水的密度;k为表面波波数。
由式(5)可以看出,表面波的本征相速度c0只与波长有关,与波的振幅无关。而且风速稳定后风生流场的速度ud也是稳定不变的,因此可以通过表面波的相速度的变化来测量表面扰动流场速度。
表面波的相速度c为波长λ与周期T之比
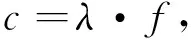
(6)
相速度c又可表达为
(7)
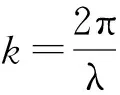
根据式(6)和(7),计算表面波的相速度可以有两种方法:1)波频率法:该方法需要计算某一波长表面波的频率,在这种情况下为了获得高的频率分辨率必然会损失时间分辨率。但此方法是在频域中进行处理,其抗噪性能较好。2)波相位法:通过计算表面波的相位差,根据式(7)计算表面波速。由于线阵CCD的扫描频率很高,因此本方法的优势是时间分辨率很高;但是其抗噪性能略差。
为了获取较高时间分辨率的流场信息,选择波相位法计算表面波相速度。在数据处理中为了减小噪声对测量结果的影响,采用了如下方法提高抗干扰性能:1)对原始数据进行自适应的二维频域滤波;2)对计算波相速度的时间间隔选择进行了优化;3)多台线阵CCD相机数据进行平均;4)对不同波长的测量结果进行平均处理。
测量表面波相速度流程图如图7所示,其中几何校正及光强斜率转换和斜率噪声抑制在第1部分中已有详细描述。下面说明上述步骤中的相位信息提取及修正和表面波相速度计算。
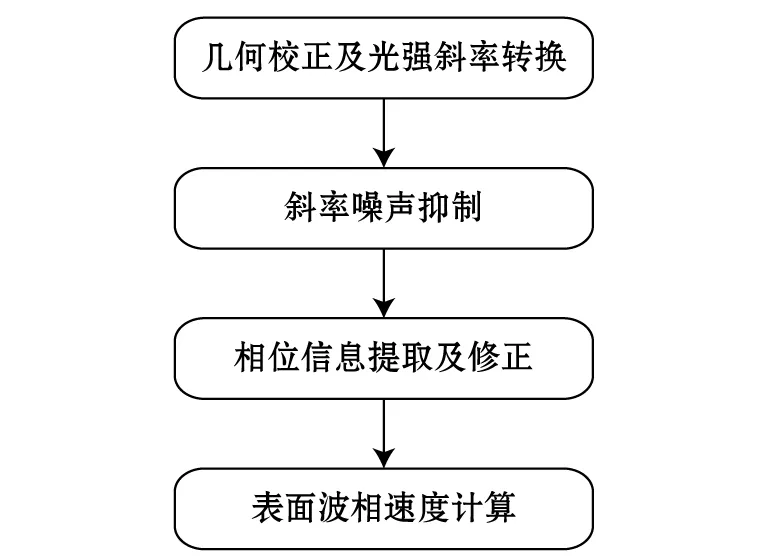
图7 相速度测量步骤Fig.7 Steps of phase velocity measurement
1)相位信息提取及修正
在获得空时二维分布的表面波斜率后,首先对每个时间点的斜率数据进行一维空间傅里叶变换,傅里叶变换后的每个频点(也就是波数点)就代表了不同的波长,某个傅里叶频点的相位随时间的变化就代表了某个波长表面波在不同时刻的相位变化。
由于线阵CCD的自身存储空间有限,在其离线采集完一帧数据后需要将数据传输回主控电脑才可以开始下一帧数据的采集。因此帧间间隔并不稳定。由此导致相位数据在帧间会有小幅度的跳变,使得相位差在帧间切换时刻误差很大,可以采用其相邻数据经过插值后得到的新的相位差信号对其进行修正。
2)表面波相速度计算
根据式(7)就可以计算表面波相速度。假设距离维傅里叶变换后某个频点(假定其对应表面波波数为k0)在t0时刻的相位为φ(k0,t0),在时刻t1=t0+Δt的相位为φ(k0,t1),那么这个波长波浪的角频率为
(8)
实验于2013-03在解放军理工大学分层流实验水槽中进行。该水槽的长、宽和高分别为12.0,1.5 和1.2 m,具备造风以及造内波的功能,测量装置示意图如图1所示。
在获得表面波的空时二维分布斜率后,可计算不同波长表面波的连续相位变化。图8即为波长4.57 cm的表面波在1 s内的相位变化。经过相位修正方法修正后,即可根据式(7)计算表面波相速度。
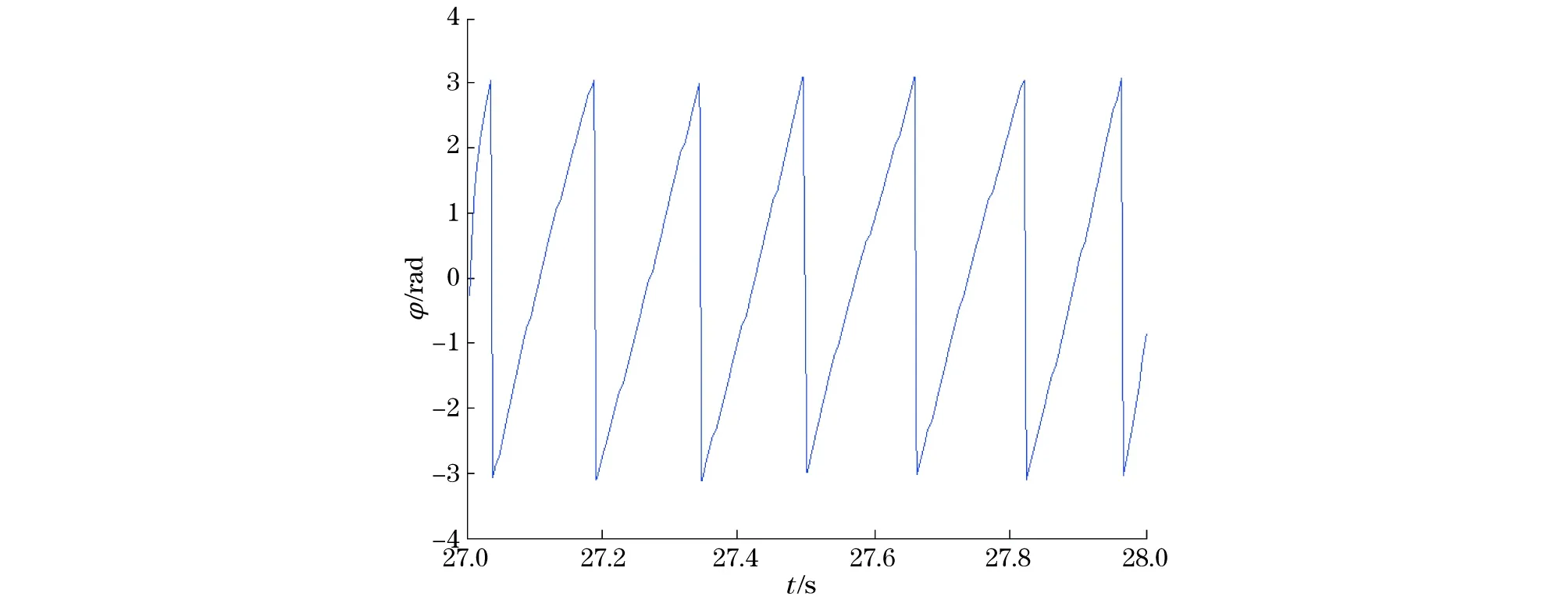
图8 波长为4.57 cm的表面波在1 s内的相位变化Fig.8 Phase variation within 1 second of a surface wave with wavelength of 4.57 cm
根据式(8),在计算表面波相速度时,选择不同的时间间隔对测量结果精度的影响是不同的。图9即为波长分别为2.08和1.52 cm的表面波相速度测量精度与时间间隔的关系曲线。
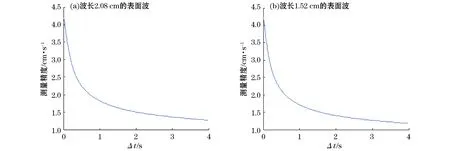
图9 表面波相速度测量精度与时间间隔关系Fig.9 Relationship between the measurement accuracy and the measurement time interval
可以明显看出,在选择时间间隔Δt≥2.5 s时,单波长的表面波相速度测量精度优于1.5 m/s,数据处理时取多个波长平均值可进一步提高。因此在计算波相速度时,统一选取时间间隔为2.5 s。
图10为波长分别为4.57,1.76和0.76 cm的表面波在一次内波实验中相速度测量结果。由图10可以看出,虽然不同波长的表面波相速度大小不同(这是由于波浪色散关系导致的),但在内波经过时引起的速度变化幅值和变化时间点是基本一致的,例如内波第一次经过观测区域时速度下降3~4 cm/s,整个观测时间内最大的速度变化值在6~7 cm/s,这种表面波相速度上的变化就是内波传播引起的表面弱流场导致的。
得到表面波相速度后,将此相速度与内波经过前的相速度均值相减,便可得到内波传播引起的表面扰动流场速度。为了减小误差,可以将多个波长表面波计算得出的表面流场进行平均处理,得到的最终结果如图11所示。
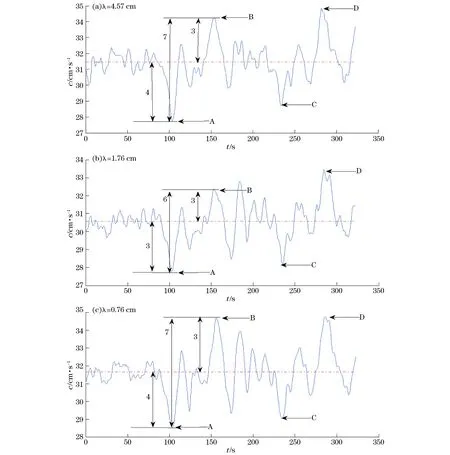
注:图中ABCD点分别代表内波第一次和第二次经过观测区域时所测相速度的波谷和波峰图10 不同波长表面波相速度Fig.10 Phase velocity of waves with different wavelength
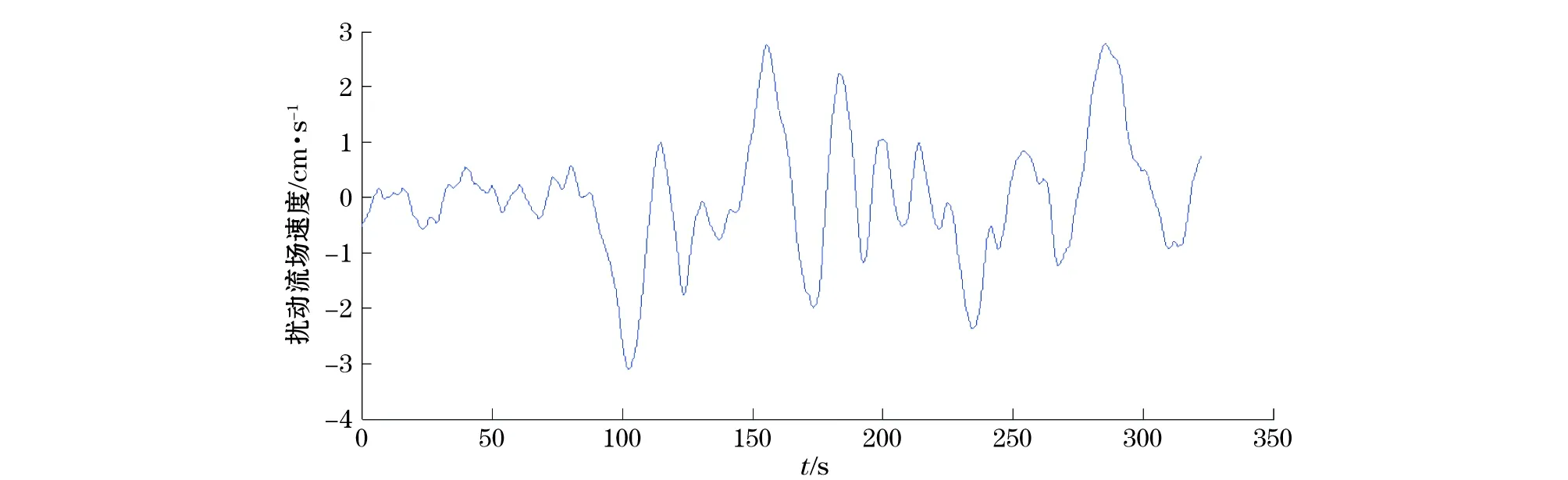
图11 内波激发的表面扰动流场速度Fig.11 Disturbed current stimulated by internal wave
3 内波对表面波调制的实验结果分析
在同步获取水面波谱和流场后就可以对波流调制模型进行分析,波流调制一般采用式(9)进行描述[7-8]:
(9)
式中,μ为松弛率;N为作用量谱,它与波高谱的关系为
(10)
φ(x,k,t)=
(11)
式中,cp和ω0分别对应表面波的相速度和角频率;u*为摩擦风速。Plant在1982年在水槽中测得的松弛率的参数化表达式[10]:
(12)
本文中采用内波来激发表面变化流场,并同时在水面吹风,产生表面风生波浪。该实验在解放军理工大学流体力学实验室开展,实验装置示意图如图1所示。该水槽是一个分层流水槽,通过盐度分层来形成垂直向的密度变化(试验中上层淡水约0.3m,下层盐水约0.5m,中间过渡层的最大浮频率约为1.6),在水槽的右侧有一个内波造波机激发内波,内波从右侧向左侧传播,本文中实验中内波造波机激发的内波包括5,7和10cm三种振幅。在水槽的上方封装了一个密封风道,风道左侧留有一个入风口和一个蜂窝整流器,蜂窝整流器的作用是使得入风更均匀,风道右侧有一个变频风扇通过吸风的方式在水面上产生风生波。
式(11)和(12)中需要用到摩擦风速u*,该数值可以通过下式进行计算[11]
(13)
式中,U(z)为高度z处的风速;κ0=0.42为卡尔曼常数。在计算了u*后同样可以利用式(13)将风速转换到海洋实验中通常采用的海面高10m处的风速U10,对式(13)两边进行积分可得
(14)
式中,z*为粗糙长度,这里采用文献[12]中的计算公式来计算z*
(15)
图12是以风扇转速9Hz为例,给出了用毕托管测量的风速随高度的变化剖面及其拟合曲线。
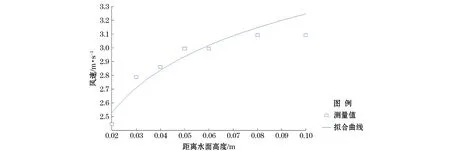
图12 风扇转速9 Hz时测量的风速剖面Fig.12 Wind speed profile when blower's frequency is 9 Hz
实验中用到了4种风速,其摩擦风速以及等效10m高处风速如表1所示。

表1 风扇转速、摩擦风速以及等效10 m风速对应表
在用线阵CCD获取波浪谱和流场后(为了降低噪声,本文中的波浪谱数据和流场数据采用的是6台CCD测量值的平均值),就可以依据式(10)计算松弛率,图13和图14为实测数据与Plant模型和Hughes模型进行对比的结果。
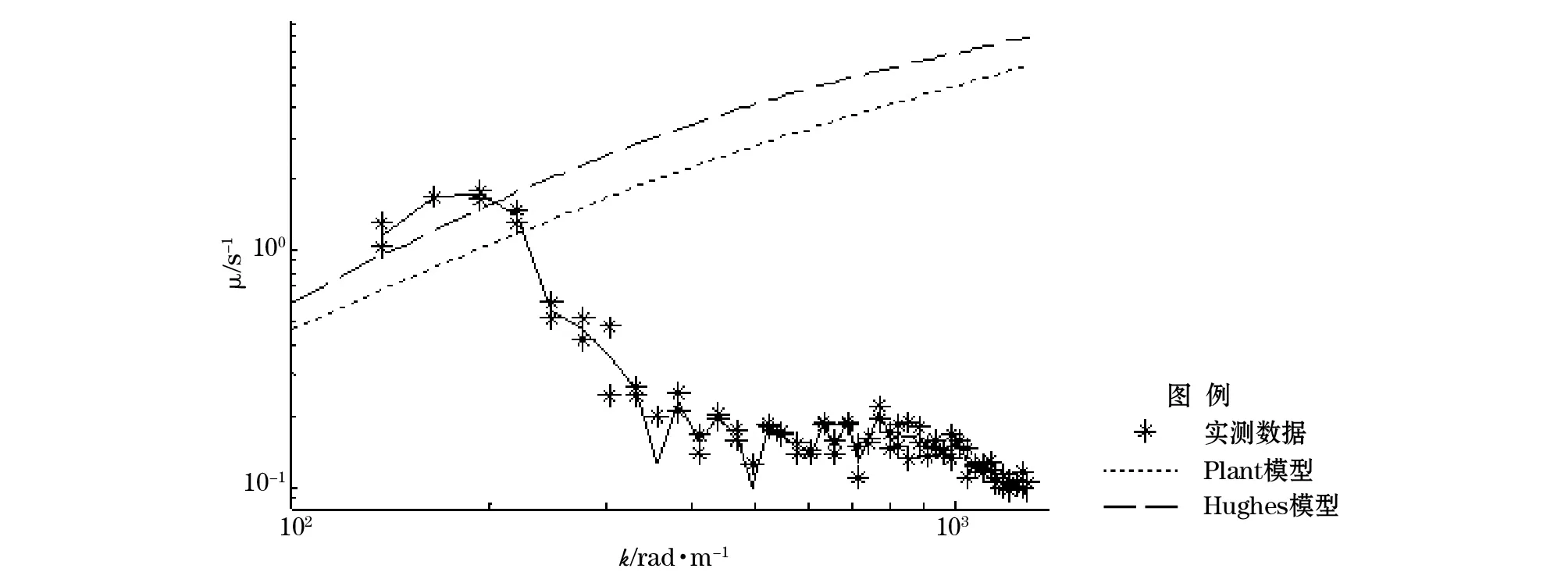
图13 风速5.3 m/s情况下的实测与Plant模型和Hughes模型松弛率对比Fig.13 Comparison of relaxation rate of Plant model, Hughes model, and our experiment when wind speed is 5.3 m/s
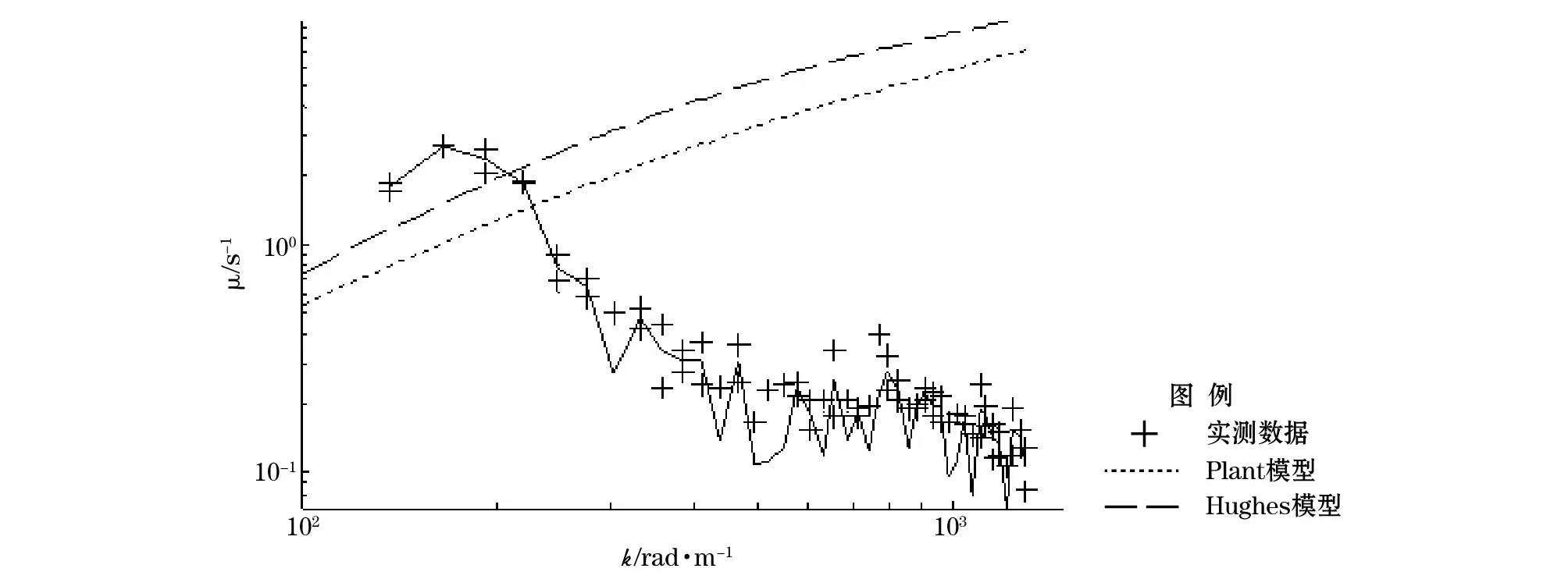
图14 风速5.893 m/s情况下的实测与Plant模型和Hughes模型松弛率对比Fig.14 The comparison between Plant model, Hughes model and measured data for wind speed 5.893 m/s
从图13和14可以看出当波数小于200(对应波长为大于3.1 cm的波浪)时,实测结果与经典的Hughes模型和Plant模型吻合较好,但是当波数大于200(对应波长为小于3.1 cm的波浪)时松弛率发生了明显的下降,与经典的模型有很大的出入。对这两种经典模型,前人基本上只对3 cm以上波长进行过验证,更小尺度的松弛率模型国际上也没有见到报道,本次试验结果说明3 cm以下的小尺度波谱的波流调制效应原有的模型不能完全解释实验现象,对本次试验结果进一步完善和给出物理解释还需要开展大量的工作。
4结论
为了对海洋遥感中的波流调制作用进行研究,需要对表面波谱和流场进行同步测量。利用本文介绍的基于线阵CCD的方法,可以对水槽中的表面波谱和表面扰动流场进行同步高精度测量,克服了传统传感器难以实现波浪谱和流场同步观测的问题。实验结果表明,对表面波测量的空间分辨率和时间分辨率分别为0.38 mm和1/300 s,对扰动流场速度的测量精度为0.3 cm/s,满足对小尺度波浪的波流调制效应的研究,可以成为研究波流调制效应的有效工具。
松弛率是波浪调制效应中非常关键的因素,现有的经典松弛率模型只在波长3 cm以上的波谱进行过有效的验证,该模型是否满足更小尺度波浪谱的波流调制效应国际上并没有公开的报道。本文的测量结果计算得出的松弛率与现有经典模型的预测结果在波长3 cm以上比较吻合,但波长小于3 cm时有较大差异,这也表明原有的经典模型不能满足更小尺度的波流调制效应,要发展适用于波长小于3 cm的波流调制效应模型还需要开展更深入的实验和理论研究。
致谢:解放军理工大学魏岗教授、研究生张原铭、陈祥瑞,上海交通大学尤云祥教授、胡天群研究员以及研究生王宏伟等人为本文提供了实验环境并提供了实验环境的浮力频率、密度剖面、风速剖面等测量数据。
参考文献(References):
[1]APEL J R, JACKSON C R. Synthetic aperture radar marine user′s manual[EB/OL]. [2015-04-10].http:∥www.sarusersmanual.com
[2]CHONG J S, OUYANG Y, LI F. Ocean internal wave detection by synthetic aperture radar[M]. Beijing:Ocean Press,2010.种劲松,欧阳越,李飞.合成孔径雷达图像海洋内波探测[M]. 北京:海洋出版社,2010.
[3]SKOLNIK M. Opportunities in radar-2002[J]. Electronics & Communication Engineering Journal, 2002, 14(12): 263-272.
[4]TITOV V, BAKHANOV V, ERMAKOV S, et al. Development of optical remote sensing technique for monitoring of water basins[C]∥Proceedings of the SPIE 8532, Remote Sensing of the Ocean, Sea Ice, Coastal Waters, and Large Water Regions 2012, 85320J (October 19, 2012).
[5]TITOV V, BAKHANNOV V, LUCHININ A, et al. Remote sensing of sea surface features by optical RTI images [C]∥Remote Sensing of the Ocean, Sea Ice, Coastal Waters, and Large Water Regions 2013, 88880J (October 23, 2013).
[6]WEN S C. Ocean wave theory and computation principal[M]. Beijing:Science Press, 1984.文圣常. 海浪理论与计算原理[M]. 北京:科学出版社, 1984.
[7]LYZENGA D R, BENNETT J R. Full-spectrum modeling of synthetic aperture radar internal wave signatures[J]. Journal of Geophysical Research-Oceans, 1988, 93(C10):12345-12354.
[8]ALPERS W, HENNINGS I. A theory of the imaging mechanism of underwater bottom topography by real and synthetic aperture radar[J]. Journal of Geophysical Research-Oceans, 1984, 89(C6):529-546.
[9]HUGHES B A. The effect of internal waves on surface wind waves 2 theoretical analysis[J]. Journal of Geophysical Research-Oceans,1978, 83(C1): 455-465.
[10]PLANT W J. A relationship between wind stress and wave slope[J].Journal of Geophysical Research-Atmospheres, 1982,87(1):1961-1967.
[11]HILLIPS O M. The dynamics of the upper ocean (Second edition)[M].New York:Cambridge University Press,1977.
[12]KELLER M R, KELLER W C, PLANT W J. A wave tank study of the dependence of X band cross sections on wind speed and water temperature[J].Journal of Geophysical Research, 1992, 97 (C4): 5771-5792.
Received: April 19, 2015
*收稿日期:2015-04-19
作者简介:杜文超(1978-),男,黑龙江哈尔滨人,工程师,博士,主要从事SAR信号与信息处理方面研究. E-mial:zfn1978@aliyun.com *通讯作者:王小青(1978-), 男, 江西吉安人,副研究员,博士,主要从事SAR海洋遥感方面研究.E-mail:huadaqq@126.com(李燕编辑)
中图分类号:P73
文献标识码:A
文章编号:1671-6647(2016)02-0280-12
doi:10.3969/j.issn.1671-6647.2016.02.013
Modulation Effects of Current on Waves Based on Experiments in Water Tank Using Linear Array CCD
DU Wen-chao1,WANG Xiao-qing2,3, LIU Li2,3, CHEN Peng-zhen2,3
(1.MilitaryRepresentativeOfficeinTianjin,EquipmentDepartmentofNavy, Beijing 100070, China;2.InstituteofElectronics,ChineseAcademyofSciences, Beijing 100190, China;3.ScienceandTechnologyonMicrowaveImagingLaboratory, Beijing 100190, China)
Abstract:Modulation effects of current on waves refer to the increase or decreaset of ocean surface small scale waves resulted from the convergence or divergence generated by ununiform ocean surface current. It is the key mechanism for microwave remote sensing of many oceanic phenomena such as internal waves, topography of shallow water, and ocean fronts, etc. The modulation effects, which are related to many factors like wind speed, ocean wave spectra, surface current, etc, are very complicated and difficult to be reproduced through experiments in ocean. However, the such experiments can be repeated and the modulation effects can be easily measured in a water tank in laboratory. In this paper, a method for measuring surface wave spectra and current based on CCD linear array is proposed, and an experiment for internal wave modulation effects observed by the CCD linear array is performed in a stratified flow. The experiment results show that the proposed method base on CCD linear array is efficient for measuring the modulation effects and is especially suitable for measuring modulation effect on the waves with wavelength between cm-mm. The results also show that the relax rate is different from classical modulation model when the wavelength of the modulated wave is less than 3 cm.
Key words:linear array CCD; tank experiment; surface disturbance current; relax rate
资助项目:国家自然科学基金项目——海面受限波雷达信号特性研究(41276185)
