北太平洋中尺度涡季节和年际变化的统计分析*
2016-07-27祖永灿高晓倩孙双文
祖永灿,方 越,高晓倩,孙双文
(国家海洋局 第一海洋研究所 海洋与气候研究中心,山东 青岛 266061)
北太平洋中尺度涡季节和年际变化的统计分析*
祖永灿,方越*,高晓倩,孙双文
(国家海洋局 第一海洋研究所 海洋与气候研究中心,山东 青岛 266061)
摘要:依据1993-01-2014-10由卫星高度计资料导出的地转流异常场数据,用几何方法探测识别并追踪了北太平洋的中尺度涡,统计了涡旋的半径、移动距离和移动速率,发现它们近似服从对数正态分布。进一步的分析发现,北太平洋涡旋生成数量存在着显著的季节变化:在冬季涡旋生成的数量最多而夏季生成的数量最少;夏季与冬季相比,涡旋生成数量减少的区域主要集中在15°~35°N。此外,北太平洋涡旋生成数量还存在着显著的年际变化;各个季节对全年变化的方差贡献量值相当。不论是季节变化还是年际变化,涡旋生成数量的变化与SST的变化均是反相,这是因为SST变化改变了上层海洋的层结强度进而影响了涡旋的生成,但该物理机制还需要进一步的分析和验证。
关键词:北太平洋;中尺度涡;季节变化;年际变化;海表面温度
中尺度涡是上层海洋中一种显著的海洋现象[1],空间尺度在几十至几百公里,时间尺度在数十天至数百天,其动能占到全球海洋总动能的90%[2],输运的水体在全球范围内达到30~40 Sv(1 Sv=106m3·s-1)[3-4],因此中尺度涡在海洋循环中有着重要的作用。与此同时,涡旋中心所携带的水体随着涡旋的移动而移动,从而造成纬向热量和盐度的净输运[5]。而这种由涡旋诱生的热通量对海洋的热平衡具有同样的重要作用[6-7]。
随着20世纪90年代一系列海洋卫星投入使用,海洋资料日益丰富,中尺度涡旋的研究也日益活跃。基于卫星高度计资料探测和追踪涡旋的相关研究也有了许多成果[2-5,8-14],提出了多种中尺度涡自动探测方法,这些方法可分为3种主要类型:1)基于物理参数的算法;2)基于流体几何学的算法;3)既有物理参数又有流体几何学的混合算法[11]。Nencioli等提出一种基于地转流异常场的几何算法(vector geometry method,VG),该方法属于第二种类型的算法,是完全依据流场中的几何学特征来判定的,其探测成功率更高同时探测多余率也更低[11-12]。
关于中尺度涡的季节变化以及涡旋生成的影响因素也有相关的研究。其中,Liu等[12]使用VG方法对北太平洋副热带逆流区1993-2010年生命周期不少于8周的中尺度涡旋进行了统计分析,结果表明涡旋生成具有较强的年际变化和季节变化,并且气旋涡和反气旋涡的生成变化比较一致,其中1、2、3月涡旋的生成量最多,7、8、9月涡旋的生成量最少。而郑聪聪[16]使用SSHA闭合等值线方法(第1类型的探测方法)对北太平洋在1993-2011年产生的中尺度涡进行了识别追踪并统计分析了该区域中尺度涡的时空分布和运动特征。其结果表明中尺度涡的生成有明显的季节变化,并且3、4、5月涡旋的生成量最多,而9、10、11月涡旋的生成量最少。这两个研究结果的差异可能主要是因为选取的涡旋探测方法、涡旋生命周期选取的条件以及研究区域的不同造成的。
Liu等[12]指出在副热带逆流区涡旋的时空变化与海表面温度(SST)的锋面强度有关。Ma等[13]利用VG方法对黑潮回旋区域1993-2011年的中尺度涡进行了统计并用相关性分析说明了在年际时间尺度上涡旋的活动受风应力旋度和海表面温度的经向梯度影响较大,同时背景流的强度和方向对涡旋的生成也有影响。Qiu[17]以及Qiu和Chen[18]利用卫星高度计资料研究了北太平洋副热带逆流区涡动能的年际变化,并指出斜压不稳定性对涡旋生成的重要作用。
本文将利用VG方法探测和追踪北太平洋中尺度涡,通过统计的方法找出涡旋半径、移动距离和移动速率的分布规律,揭示涡旋生成的季节变化和年际变化特征,并在季节变化的空间分布特征和年际尺度上的相关性分析这两个方面探讨涡旋生成的影响因素。
1数据和方法
1.1数据
本文用到的地转流异常数据是由法国AVISO网站提供的。该数据是由海面高度异常(SLA)根据地转关系得到,具体公式:
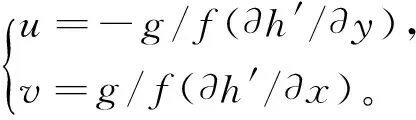
(1)
式中,u和v分别是地转流异常场的纬向和经向分量;h′是海表面高度异常;g是重力加速度;f是科氏参数。AVISO提供了ERS-1、ERS-2、Jason-1和Jason-2等卫星以及多个卫星融合的数据,并提供了实时和延时两种数据模式。2014-05 AVISO更新了数据,并首次融合了2011年发射升空的中国海洋二号卫星数据(HY-2)。融合后的数据与之前的相比,不仅是增加了HY-2卫星的数据,而且SLA的参考周期也由原来的1993-1999年的7 a更改为1993-2012年的20 a,空间分辨率由0.33°提高到0.25°。本文选取的是1993-01-2014-10融合后的地转流异常场数据,空间分辨率是0.25°,时间分辨率是1 d,范围是(5~60°N,120°E~75°W),其中2014-06-10为实时模式的数据,其余为延时模式的数据(ftp.aviso.altimetry.fr/global/dt/upd/msla/merged/)。本文为了更准确探测涡旋同时减少计算量,用双线性插值将空间分辨率提高至0.125°,时间以每7 d做平均,将时间分辨率降至7 d。
海表面温度和风场数据均是从欧洲中期气象预报中心(ECMWF)的ERA-Interim数据集(http:∥apps.ecmwf.int/datasets/)中选取得到,其时间跨度为1993-01—2014-12,空间分辨率为0.5°,其中风场是海表面10 m处的经向和纬向分量。
海洋气候态的垂向温盐数据选取美国国家海洋数据中心的WOA13数据,选取年平均的数据,空间分辨率为1°,水深范围0~5 500 m,垂向分层102层,比WOA09中33层的垂向分辨率更高(http:∥www.nodc.noaa.gov/cgi-bin/OC5/woa13/woa13.pl)。
1.2方法
本研究探测涡旋采用的是VG方法,该方法利用流场异常场来探测涡旋,主要基于以下4个约束条件:1)沿东西方向穿过涡旋中心时,涡中心两侧的v方向相反且离涡中心越远值越大;2)沿南北方向穿过涡旋中心时,涡中心两侧的u方向相反且离涡中心越远值越大,并且u的旋转方向与v的旋转方向一致;3)涡旋中心的速度值有局部最小值;4)涡中心附近,速度向量的旋转方向一致并且两个相邻的速度向量在同一象限或相邻象限。在探测时需要两个参数a和b,参数a是前两个约束条件中在东西和南北方向上检测v和u时增加的网格点数,参数b定义了确定局部速度最小值时的寻找区域,该区域由某一点周围的b个网格点扩展而成。参考Liu等[12]和Ma等[13],本文分别取a=3和b=2。涡旋的边界定义为在涡旋中心外围流函数最外层的闭合等值线,这就确定了涡旋的中心及边界,同时根据u和v的旋转方向可以确定涡旋的类型[11-12]。
在追踪涡旋时首先确定搜索半径,不同方法搜索半径也不相同,通常搜索半径为背景流场速度乘以数据时间周期。由于北太平洋平均背景流场为0.18 m/s,所使用的数据时间间隔是1周,所以我们在探测追踪涡旋时搜索半径为108 km。追踪涡旋时,先在t时刻找到涡旋中心,在t+1时刻以t时刻涡旋的中心为中心,如果在搜索半径范围内找到同类型的涡旋则认为是同一个涡旋;如果没有找到同类型涡旋,则继续搜索t+2时刻并且搜索半径扩大1.5倍,如果在t+2时刻仍没有找到同类型涡旋,则结束本次搜索,认为t时刻找到的涡旋已经消亡。这样在确定好单个涡旋之后便可以追踪该涡旋,从而得到各个涡旋在其生命周期中不同时刻的位置和大小以及移动路径[11-13]。
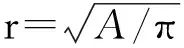
2统计结果
为了准确合理地描述涡旋的基本性质,我们只统计分析生命周期不少于8周的涡旋[12]。1993-01-2014-10期间,在北太平洋(统计海域可参照图4中彩色覆盖区域)一共搜索到39 248个涡旋,其中气旋涡20 373个,反气旋涡18 875个,气旋涡比反气旋涡约多7%左右。气旋涡和反气旋涡的生命周期、半径、移动距离和移动速率这四个参数的分布趋势基本一致。它们的平均生命周期分别为18.7和19.8周,平均半径分别为45和46 km,平均移动距离分别为559和562 km,平均移动速率分别为5.1和5.0 cm/s。其中涡旋的平均生命周期、平均移动距离和平均移动速率均与Cheng等[14]的结果比较一致,但涡旋的平均半径与他们的统计结果(70~80 km)相比偏小,究其原因主要是因为这两个研究中的涡旋探测方法对涡旋边界的定义不同所导致,并且本文选取的生命周期不少于8周的条件也是一个重要因素。
在大洋中,气旋涡和反气旋涡的数量并不相等,而且它们各自的移动方向也有明显的差异,因此是否能准确抓住涡旋的这两个特征是判断一种涡旋探测方法有效性的一个重要判别标准。为检测本文中所采用的涡旋探测方法的可靠性,我们将所有气旋涡和反气旋涡的生成位置都放在同一个点(图1中的(0,0)点),每条折线代表一个涡旋从生成到消亡过程中的实际运动轨迹。可以看出涡旋主要以自东向西移动为主,在向西移动的过程中反气旋涡有向赤道方向偏移的趋势而气旋涡则有向极地偏移的趋势。Chelton等[15]统计了全球10°~50°N内生命周期大于16周的气旋涡和反气旋涡的经向偏移,发现反气旋涡以偏向赤道为主,气旋涡以偏向极地为主,其比例分别为70%和55%。本文的统计数据与这一结果十分一致。
涡旋的半径、移动距离和移动速度是描述涡旋特征3个重要参数,判断其统计分布类型是描述涡旋特征的另外一个重要方法。Liu等[12]使用VG方法探测追踪了1993-2010年北太平洋副热带逆流区的涡旋,通过统计分析生命周期不少于8周的涡旋,发现这些涡旋的半径近似服从正态分布。而Cheng等[14]使用Okubo-Weiss方法(OW方法;属于第1类型的探测方法)探测追踪了在1992-10-2012-12北太平洋的涡旋,结果表明涡旋的半径、传播速度均近似服从瑞利分布。
由于本文采用的是与Liu等相同的VG方法,但探测追踪涡旋的区域扩展到整个北太平洋,就区域而言与Cheng等的一致。为了研究基于本文涡旋探测追踪数据的统计分布特征,我们分别用正态分布和瑞利分布去拟合涡旋半径、移动距离和移动速率的分布,发现正态分布和瑞利分布均有较大的偏差。然而,如果采用对数正态分布去拟合涡旋的3个参数却可以显著减小拟合的误差从而达到较好的拟合效果。值得注意的是,本文与Cheng等最重要的差别是所采用的涡旋探测方法的不同。从这两个研究所得到的涡旋特征分布函数的不同可以看出不同的涡旋探测追踪方法所得到的涡旋半径、移动距离和移动速率是有差别的。就涡旋的探测成功率而言,VG方法要优于OW方法,因此涡旋半径、移动距离和移动速率符合对数正态分布可能更加合理一些。
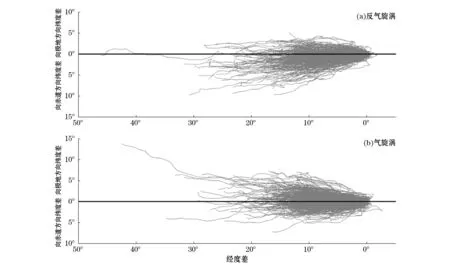
图1 生命周期大于16周的涡旋移动轨迹Fig.1 Tracks of anticyclonic (upper panel) and cyclonic (lower panel) eddies with lifetime >16 weeks
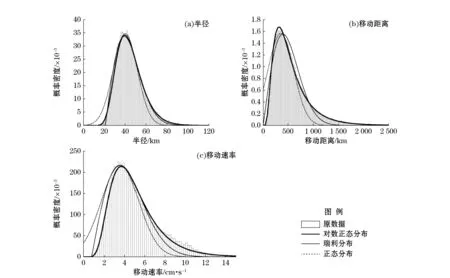
图2 涡旋半径、移动距离和移动速率的不同分布类型的拟合Fig.2 Histograms of eddy radius,travel distance and travel speed and fitting with different statistical distribution functions
3涡旋生成数量的季节变化
在海洋中,涡旋的生成数量是随着季节的变化而变化的。图3中显示了北太平洋气旋涡(细实线)和反气旋涡(虚线)在各个月份的平均生成数量以及SST的季节变化(粗黑线)。从图中可以看出,气旋涡与反气旋涡具有相似的季节变化特征,均是在冬季(1-3月)的生成数量最多而夏季(7-9月)是一年中涡旋生成数量最少的季节,夏季涡旋生成的数量约为冬季生成数量的80%。涡旋生成数量的这种季节变化特征与北太平洋SST的季节变化恰恰相反,二者呈负相关关系。如果二者之间的这种统计关系的背后的确存在着某种物理机制的联系,那么最有可能的是SST的变化可以影响涡旋的生成数量,反之则不太可能。这主要是因为SST的季节变化是太阳辐射的变化直接导致的,不可能是涡旋数量的变化所导致。

图3 气旋涡和反气旋涡生成量的季节变化Fig.3 Seasonal variations of the number of cyclonic and anticyclonic eddies
为了研究涡旋生成量在不同季节的水平分布特征及其变化,我们选取了涡旋生成量最多的冬季和生成量最少的夏季进行对比分析。图4a和图4b分别显示的是冬季和夏季涡旋多年平均生成数量的水平分布,图中颜色代表的是在5°×5°区域内涡旋在该季节的多年平均生成量。可以看到,冬季涡旋的生成主要集中在日界线以东、15°~50°N的区域内,而在夏季涡旋的主要生成区位于160°W以东、35°~50°N。图4c显示的是冬、夏两季涡旋生成量的差异(前者减去后者)分布图。从该图中可以看到,与冬季相比北太平洋大部分海域夏季涡旋生成量普遍减少,但数量变化最为显著的区域是在15°~35°N的带状区域。涡旋生成数量这种在纬向上相对一致的季节变化与SST季节变化的空间分布特征十分一致,这与上面我们推测的SST季节变化影响涡旋生成数量的动力机制也是一致的。
那么,SST的季节变化是如何影响涡旋的生成数量的呢?由于不论是气旋涡还是反气旋涡,其最重要的动力结构就是伴随涡旋的地转流和由此引起的涡旋中心海水垂向运动。涡旋中心海水的垂向运动是涡旋形成的必要条件之一,或者说,当垂向运动受到抑制的时候,涡旋就难以产生。在北太平洋,当由冬季转入夏季时,随着太阳短波辐射量的增加,SST逐渐升高。当SST升高时,上层海洋的斜压性增强、层结更加稳定,不利于海水的垂向运动,从而在很大程度上抑制了涡旋的生成。图5显示的是北太平洋冬季(实线)和夏季(虚线)上层海洋层化指数(SI,定义为0~90 m海温平均值减去90~180 m海温平均值)随纬度的变化情况。
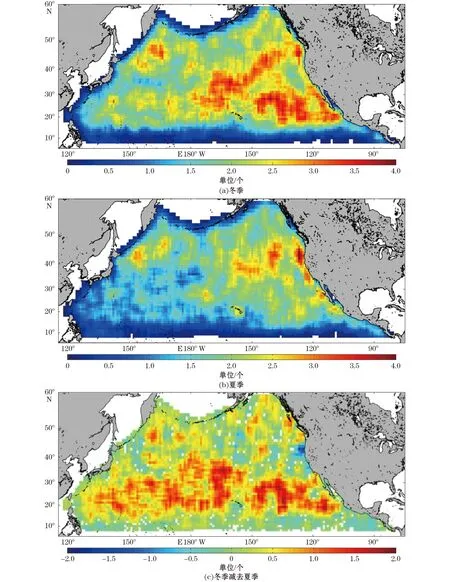
图4 涡旋生成量的空间分布Fig.4 Spatial distributions of the annual averaged number of generated eddies in 5°×5° bins
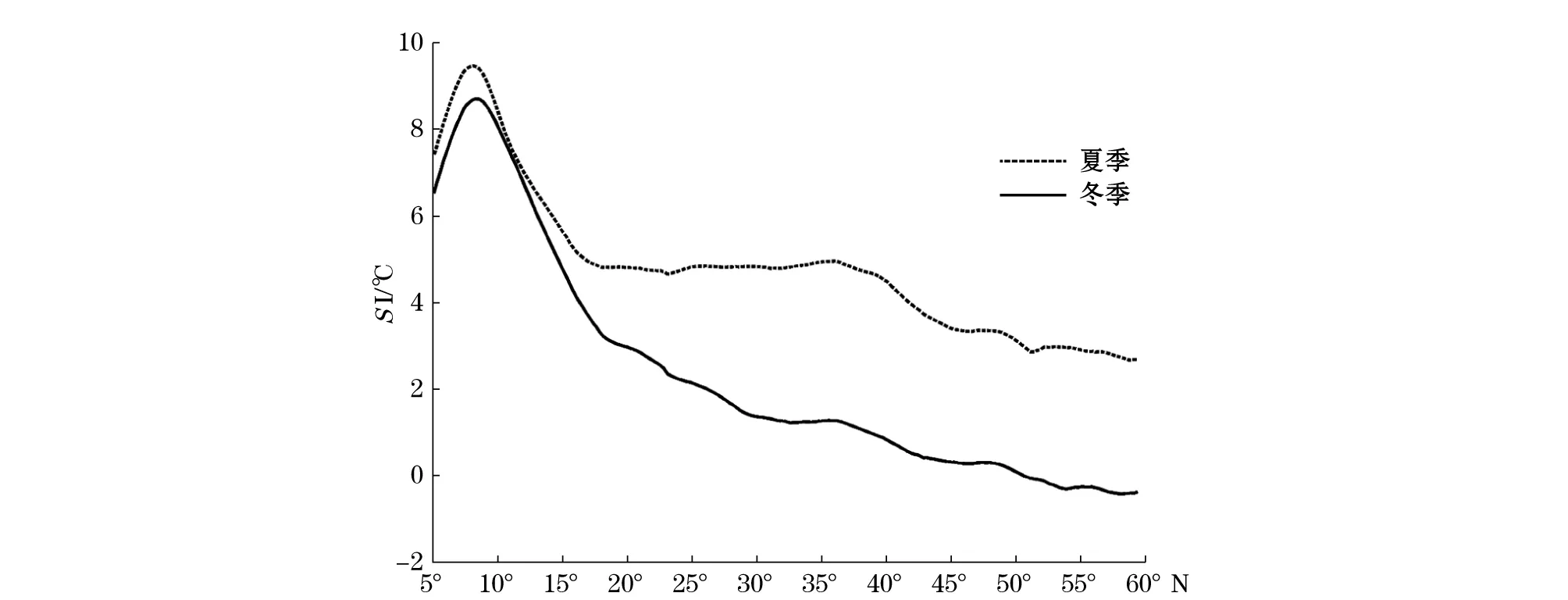
图5 北太平洋纬向平均的上层海洋层化指数Fig.5 Zonal averaged stratification index (SI) of the upper layer of the north Pacific Ocean
在计算SI之前,先对海温做了纬向平均。因此某一纬度的SI值越高说明在这一纬度上层海洋层化越强。从图5中可以看出,夏季北太平洋海洋上层的层化程度普遍高于冬季,而且在15°N以北层化的季节变化最为显著,这很好地解释了为什么夏季涡旋生成的数量要明显小于冬季(图4)。此外,上层海洋的层化程度对涡旋生成的影响并非线性的,那么这就可能存在这样一个“阈值”:当SI大于这个阈值时,涡旋生成量急剧减少;而当SI小于这个阈值时,涡旋生成量受层化的影响不明显。对照图4和图5,如果的确存在这样一个阈值,该阈值应该在4.5 ℃左右。根据图5,SI<4.5 ℃的海区在冬季位于15°N以北,而在夏季北移至35°N以北。这可以很好地解释为什么冬季和夏季涡旋生成数量差异最大的区域是15°~35°N(图4c)。
4涡旋生成数量的年际变化
目前关于涡旋生成数量年际变化的研究主要都是针对大洋西边界强流区或者具有较大流速剪切的海区,例如黑潮流经的海域和副热带逆流区。然而涡旋大量产生的区域并非在这些海区,图4a和图4b就很好地说明了这一点。因此,在本研究中我们把整个北太平洋作为一个研究区域来统计涡旋生成的数量并分析其年际变化的规律。图6a显示了北太平洋全部涡旋(粗黑线)、气旋涡(虚线)和反气旋涡(细实线)自1994年至2003年生成数量的年际变化。可以看到涡旋生成数量的年际差异十分显著,涡旋生成数量最多的1995年比最少的2003年多15%左右。气旋涡和反气旋涡生成数量的年际变化基本上是同步的,即当气旋涡数量明显异常增多(减少)时反气旋涡相对常年也是异常增多(减少)的。
为了研究涡旋生成数量年际变化中各个季节的贡献,我们分别计算了冬季、春季、夏季和秋季涡旋生成数量异常的年际变化(图6b)。在变化的一致性方面,各个季节中涡旋生成量的变化之间的相关性并不显著,表明它们的变化并不同步;但它们的变化幅度却基本相当,其标准差分别是27,20,25和23,表明各个季节对全年涡旋生成总数的年际变化的贡献基本相同,冬季的贡献相对较大。因此,涡旋生成量显著异常增多的年份(例如:1995、2001、2010年)均是由于该年多个季节中涡旋生成量均异常增多所致;对于涡旋生成量显著异常减少的年份(例如:2003年)则是由于该年多个季节中涡旋生成量均异常减少所致。
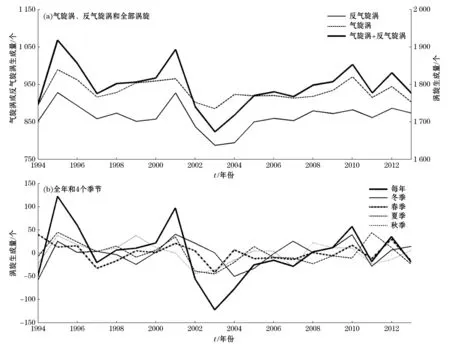
图6 涡旋生成量的年际变化Fig.6 Interannual variations of the number of eddies generated
在前文中我们谈到SST的季节变化对涡旋生成数量的影响作用。那么涡旋生成数量的年际变化是否也与SST的年际变化相关联呢?由于冬季是一年中涡旋生成最多的季节(图3),并且冬季海洋上层SI小于阈值(约4.5℃)的海区面积也最大(图5),因此我们选取冬季作为代表性季节来研究涡旋生成数量的年际变化机制。图7中显示的是北太平洋冬季涡旋生成数量异常和SST异常的时间序列。经计算,它们二者的相关系数为-0.44,并且在0.1的显著性水平上是显著相关的。这表明,在涡旋生成数量的年际变化中,SST的变化仍然是重要的影响因素。

图7 北太平洋冬季涡旋生成量异常和SST异常的年际变化Fig.7 Time series of the anomalous number of eddies (solid line) and the SST anomaly (dashed line) in winter in the north Pacific Ocean
5结语
本文利用VG方法识别和追踪了北太平洋1993-01-2014-10的中尺度涡,发现其半径、移动距离和移动速率这三个参数均近似地服从对数正态分布。通过进一步分析涡旋生成数量的季节和年际变化发现,北太平洋在冬季涡旋生成的数量最多而夏季生成的数量最少,这与SST的季节变化相反;夏季与冬季相比,涡旋生成数量减少的区域主要集中在15°~35°N。北太平洋涡旋生成数量存在着显著的年际变化;各个季节对全年变化的方差贡献量值相当。与季节变化相类似,涡旋生成数量的年际变化与SST的年际变化亦是反相,相关系数为-0.44。SST可以通过改变上层海洋的层结强度来影响涡旋的生成,但该物理机制还需要进一步分析和验证。另外,进一步的分析表明,风场的季节变化与涡旋生成数量没有明显的相关性,而有关风场对涡旋生成的影响还需要进一步探讨。
致谢:南京信息工程大学董昌明教授和刘宇副教授为涡旋探测方法研究提供了帮助。
参考文献(References):
[1]AOKI S,IMAWAKI S. Eddy activities of the surface layer in the western North Pacific detected by satellite altimeter and radiometer[J]. Journal of Oceanography, 1996, 52(4):457-474.
[2]LIN P F.Statistical analyses on mesoscale eddies inthe South China Sea and the Northwest Pacific[D].Qingdao: Institute of Oceanology, Chinese Academy of Sciences,2005. 林鹏飞. 南海和西北太平洋中尺度涡的统计特征分析[D].青岛: 中国科学院海洋研究所, 2005.
[3]ZHANG Z G,WANG W,QIU B. Oceanic mass transport by mesoscale eddies[J].Science, 2014, 345(6194):322-324.
[4]ZHANG Z G.Mesoscale eddy[D].Qingdao:Ocean University of China,2014.张正光.中尺度涡[D].青岛: 中国海洋大学, 2014.
[5]DONG C M, MCWILLIAMS J C, LIU Y, et al. Global heat and salt transports by eddy movement[J].Nature Communications, 2014, 5(2):163-180.
[6]DRIJFHOUT S S, WALSTEIJN F H. Eddy-induced heat transport in a coupled ocean atmospheric anomaly model[J].Journal of Physical Oceanography, 1998, 28(2):250-265.
[7]ROEMMICH D, GILSON J. Eddy transport of heat and thermocline waters in the North Pacific: A key to interannual/decadal climate variability[J].Journal of Physical Oceanography, 2001, 31(3):675-687.
[8]CHAIGNEAU A, GIZOLME A, GRADOS C. Mesoscale eddies off Peru in altimeter records: Identification algorithms and eddy spatio-temporal patterns[J].Progress in Oceanography, 2008, 79(2-4):106-119.
[9]ITOH S, YASUDA I. Characteristics of mesoscale eddies in the Kuroshio-Oyashio extension region detected from the distribution of the sea surface height anomaly[J].Journal of Physical Oceanography, 2010, 40(5):1018-1034.
[10]YANG G, WANG F, LI Y L, et al. Mesoscale eddies in the northwestern subtropical Pacific Ocean: Statistical characteristics and three-dimensional structures[J].Journal of Geophysical Research Oceans, 2013, 118(4):1906-1925.
[11]NENCIOLI F, DONG C M, DICKEY T, et al. A vector geometry-based eddy detection algorithm and its application to a high-resolution numerical model product and high-frequency radar surface velocities in the Southern California Bight[J].Journal of Atmospheric & Oceanic Technology, 2010, 27(3):564.
[12]LIU Y, DONG C M, GUAN Y P, et al. Eddy analysis in the subtropical zonal band of the North Pacific Ocean[J].Deep Sea Research. Part I: Oceanographic Research Papers, 2012, 68(5):54-67.
[13]MA L B,WANG Q. Mean properties of mesoscale eddies in the Kuroshio recirculation region[J].Chinese Journal of Oceanology & Limnology, 2014, 32(3):681-702.
[14]CHENG Y H, HO C R, ZHENG Q A, et al. Statistical characteristics of mesoscale eddies in the North Pacific derived from satellite altimetry[J].Remote Sensing, 2014, 6(6):5164-5183.
[15]CHELTON D B, SCHLAX M G, SAMELSO R M. Global observations of nonlinear mesoscale eddies[J].Progress in Oceanography, 2011, 91(2):167-216.
[16]ZHEANG C C,YANG Y X,WANG F M.Spatial-temporal features of eddies in the North Pacific[J].Marine Sciences,2014(10):105-112.郑聪聪, 杨宇星, 王法明. 北太平洋中尺度涡时空特征分析[J]. 海洋科学, 2014,38(10):105-112.
[17]QIU B. Seasonal eddy field modulation of the North Pacific subtropical countercurrent: Topex/Poseidon observations and theory[J].Journal of Physical Oceanography, 1999, 29(10):2471-2486.
[18]QIU B, CHEN S M. Interannual variability of the North Pacific subtropical countercurrent and its associated mesoscale eddy field[J].Journal of Physical Oceanography, 2010, 40(1):213-225.
Received: June 7, 2015
*收稿日期:2015-06-07
中图分类号:P731
文献标识码:A
文章编号:1671-6647(2016)02-0197-10
doi:10.3969/j.issn.1671-6647.2016.02.005
Seasonal and Interannual Variation of Mesoscale Eddies in the North Pacific Ocean: A Statistical Analysis
ZU Yong-can, FANG Yue, GAO Xiao-qian, SUN Shuang-wen
(CenterforOceanandClimateResearch,TheFirstInstituteofOceanography,SOA,Qingdao 266061,China)
Abstract:Surface anomalous geostrophic currents from January 1993 to October 2014, which are derived from altimetry dataset, and a geometry-based eddy detection method are used to detect and track the mesoscale eddies in the north Pacific Ocean. Statistics shows that the distributions of eddy radius, propagation distance and propagation speed can be well fit with logarithm normal distribution function. Analysis further demonstrates that the number of the eddies generated is maximum in the winter while minimum in the summer. The major difference in distribution of the eddies in winter and summer is in the region 15°-35°N. In addition, the number of eddies shows remarkable interannual variation, in which each season contributes basically equally to the variability. In both seasonal and interannual variations, the anomalous number of eddies is negatively correlated with the SST anomaly in the north Pacific Ocean. This is probably because anomalous SST changes the stratification of the upper layer of the ocean and thus affects the generation of eddies—this mechanism needs to be further verified in future study.
Key words:north Pacific Ocean; mesoscale eddy; seasonal variation; interannual variation; sea surface temperature
资助项目:国家重大科学研究计划——热带太平洋印度洋环流及其热输送对全球变暖的响应(2012CB95560);中国科学院战略先导科技专项——中国邻近大洋百年热力状况对中国气候的影响(XDA05090404);国家自然科学基金委员会-山东省人民政府联合资助海洋科学研究中心项目——海洋环境动力学和数值模拟(U1406404);中央级公益性科研院所基本科研业务费专项——西北太平洋及中国近海年代际气候变化(GY2010T02)作者简介:祖永灿(1989-),男,安徽宿州人,硕士研究生,主要从事中尺度涡方面研究.E-mail:zuyc@foxmail.com
*通讯作者:方越(1970-),男,山东青岛人,研究员,博士,主要从事海气相互作用方面研究.E-mail:yfang@fio.org.cn(陈靖编辑)
