基于变分模态分解近似熵和支持向量机的轴承故障诊断方法
2016-07-26岳应娟孙钢蔡艳平
岳应娟,孙钢,蔡艳平
(火箭军工程大学,西安 710025)
文献[1]通过仿真及试验证明了变分模态分解(Variational Mode Decomposition,VMD)对轴承故障特征频率的提取能力并提出了基于谱峭度和VMD算法的包络谱轴承故障诊断方法。但是由于包络分析法的固有缺陷,在形成包络信号时需依靠经验进行解调频带参数的选取[2],故障特征频率并不与理论值严格地一一对应,人为主观因素对诊断结果造成很大影响且难以实现自动化诊断。
近似熵(Approximate Entropy,AE)是从衡量时间序列复杂性的角度来度量信号中产生新模式的概率大小的物理量,其所需数据长度短、抗噪能力强,同时适用于随机信号和确定性信号[3]。轴承发生不同的故障时,在不同频带内信号的近似熵值会发生改变,故可以通过VMD[4]将信号分解成预设的几个频带,然后通过计算每个频带的近似熵来判断是否发生故障以及故障类型。因此,将VMD近似熵与支持向量机(Support Vector Machine,SVM)相结合,尝试用于轴承振动信号的处理,以更好的实现轴承故障的识别。
1 故障诊断方法
1.1 近似熵
近似熵是一种新的序列复杂性的度量方法,其用一个非负数表示某时间序列的复杂性,时间序列越复杂,所对应的近似熵越大,信号越趋于非平稳状态,包含的频率成分也更加丰富、系统更加复杂;而近似熵越低则表示信号越趋于周期性、信号包含的频谱越窄[5-6]。当轴承处于不同的工作状态时,振动信号的频率分布会发生不同的变化,同样近似熵在振动信号不同频带的分布也会发生相应的变化,以此作为特征量便可实现轴承不同工作状态的判别。
已知X(i)为包含N个数据点的时间序列{x(1),x(2),…,x(N)},其近似熵算法如下:
1)按照设定模式维数m重构相空间X(i),X(i)=[x(i),x(i+q),…,x(i+m-1)],其中i=1,2,…,N-m+1。
2)定义矢量距离d[X(i),X(j)]为X(i)与X(j)对应元素中的最大差值,即
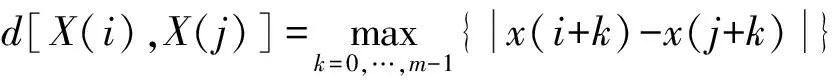
。(1)
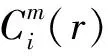
i,j=1,…,N-m+1,i≠j。
(2)
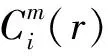
(3)
5)增加模式维数m=m+1,重复1)~4),求得Φm+1(r)。
6)定义近似熵为
ApEn(m,r,N)=Φm(r)-Φm+1(r)。
(4)
近似熵与m,r和N的取值有关,但对N的依赖程度最小,一般情况下取m=2,r=0~0.25SD, (SD为时间序列标准差)。从近似熵的计算可以看出,近似熵反映的是时间序列的自相似程度。
1.2 支持向量机
支持向量机是基于结构风险最小原理和统计学习理论的学习机器[7],其将样本空间映射到高维空间,通过解决特征空间的线性分类问题实现样本空间中的非线性分类。相比于传统学习机器,SVM能够适应非常有限的学习样本信息,且对数据维数不敏感,具有很好的推广性[8-9]。
SVM可以看作一个二分类的问题,其核心思想是寻找一个最优分类的超平面,该超平面在保证分类精度的同时,应当使分类间隔(margin)最大,如图1所示。
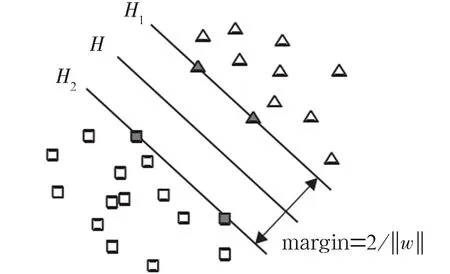
图1 支持向量机原理示意图
图1中H为分类线,在H的两侧各有一类分类样本,H1和H2分别表示距离分类线H最近的样本,H1和H2到H的距离相等且与H保持平行。分类线H的方程为w·x+b=0,对其归一化,使线性可分样本集(xi,yi),i=1,…,n,x∈Rd,y∈{-1,1} ,且满足
yi[(w·xi)+b]-1≥0;i=1,…,l。
(5)
此时的分类间隔为2/‖ω‖,若使间隔最大,则‖ω‖应当最小,易证‖ω‖2/2最小的分类面为最优分类面,位于H1和H2上的训练样本点即为支持向量。使用SVM实现分类的具体步骤为:
1)有M类的分类问题,给定其训练集
T={(x1,y1),(x2,y2),…,(xl,yl)};
xi∈Rd,i= 1,2,…,l,y∈{1,2,…,M} 。
(6)
2)对于j=1,2,…,M,把其中一类看作正类,其余M-1类看作负类,用两类支持向量机求出决策函数f(x),即
fj(x)=sgn(gj(x)),
(7)
式中:g(x)为分类平面函数。
3)判断输入x属于第J类,其中J是g1(x),g2(x),…,gM(x)中最大者的上标。
1.3 故障诊断流程
如图2所示,基于VMD近似熵和支持向量机的故障诊断方法共分以下几个步骤:1)采集轴承典型故障下的振动信号,用VMD进行初步分析;2)统计各IMF分量的近似熵,并将得到的近似熵向量作为训练样本对SVM分类器进行训练;3)将在线采集的信号或待诊断故障信号按照上述提取特征参数的方法构造待诊断故障样本,并将其输入训练好的分类器,完成在线故障诊断。
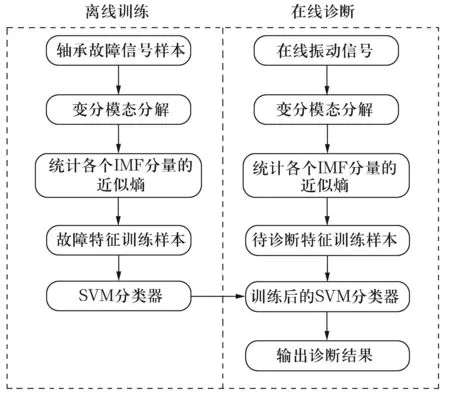
图2 基于VMD近似熵和支持向量机的轴承故障诊断流程
2 试验分析
以某变速箱轴承为研究对象,变速箱装置简图如图3所示[1]。轴承型号为KOYO1205,利用电火花在轴承的外圈沟道、内圈沟道和钢球表面各设置面积约为3 mm2的点蚀,以模拟外圈故障、内圈故障及钢球故障。变速箱运行时的负载为25 N·m,轴的转速约600 r/min(fr=10 Hz),通过B&K3560数据采集仪拾取变速箱轴承座的垂直振动信号。采集轴承在正常状态及3种故障状态下各50个振动信号样本,每个样本长度为3 000。
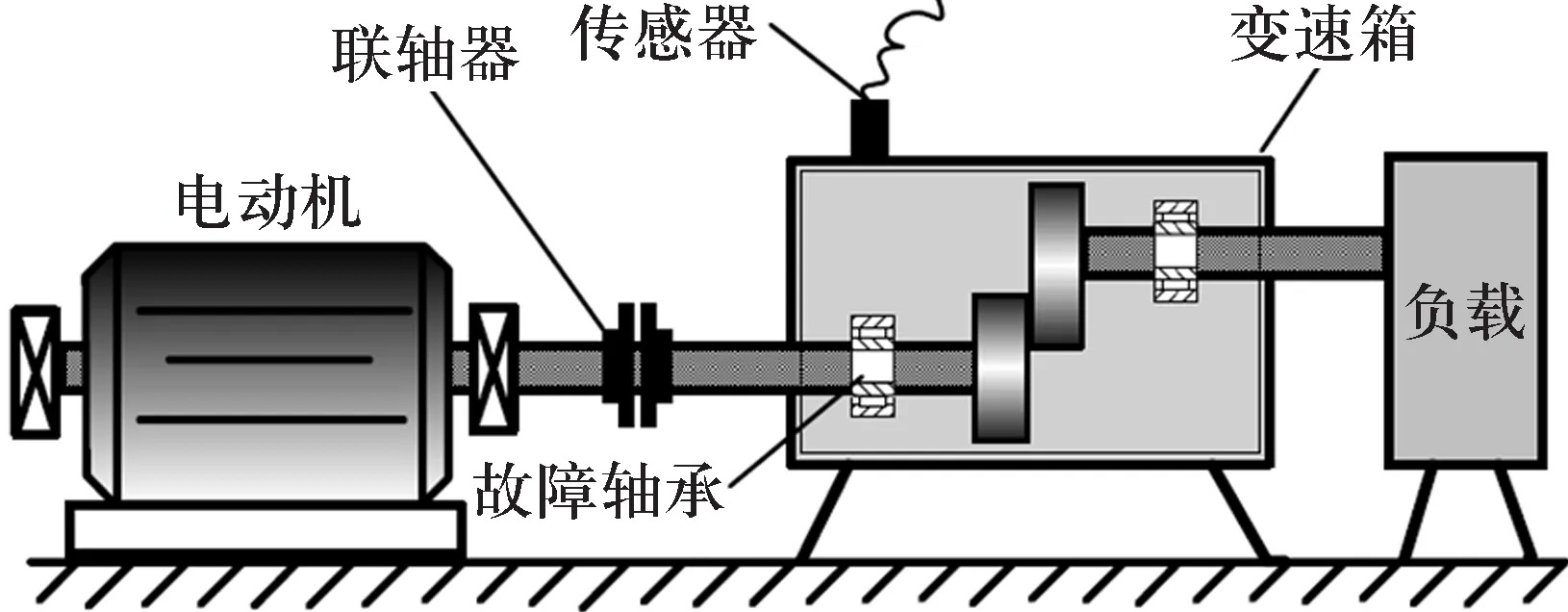
图3 变速箱装置简图
不同故障轴承实测振动信号的时域波形如图4所示,从图中很难对具体的故障类型进行判断,需对时域信号作进一步处理。
对采集到的200个试验数据分别进行VMD处理,为确保频带分解适宜,避免模态混叠现象,有利于计算各个频段的近似熵,保证实际分解信号的保真度,设定分解层数K=4,惩罚参数α=2 000,偶权值参数τ=0.3[1]。计算VMD处理后得到的IMF分量的近似熵,并将其作为特征向量,由于篇幅所限,从4种工况中各选取3个特征向量进行展示,结果见表1。
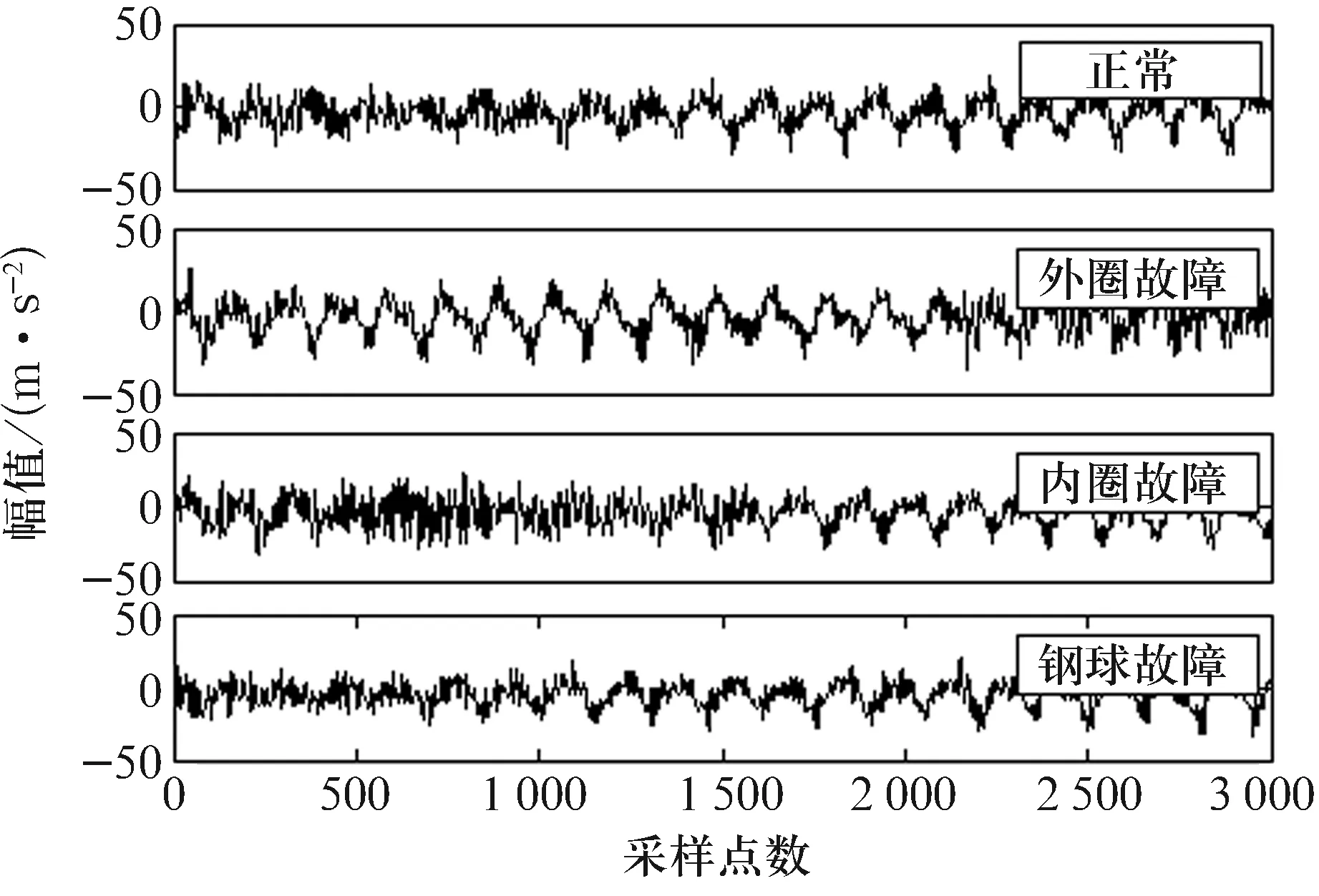
图4 不同工况下的轴承振动信号
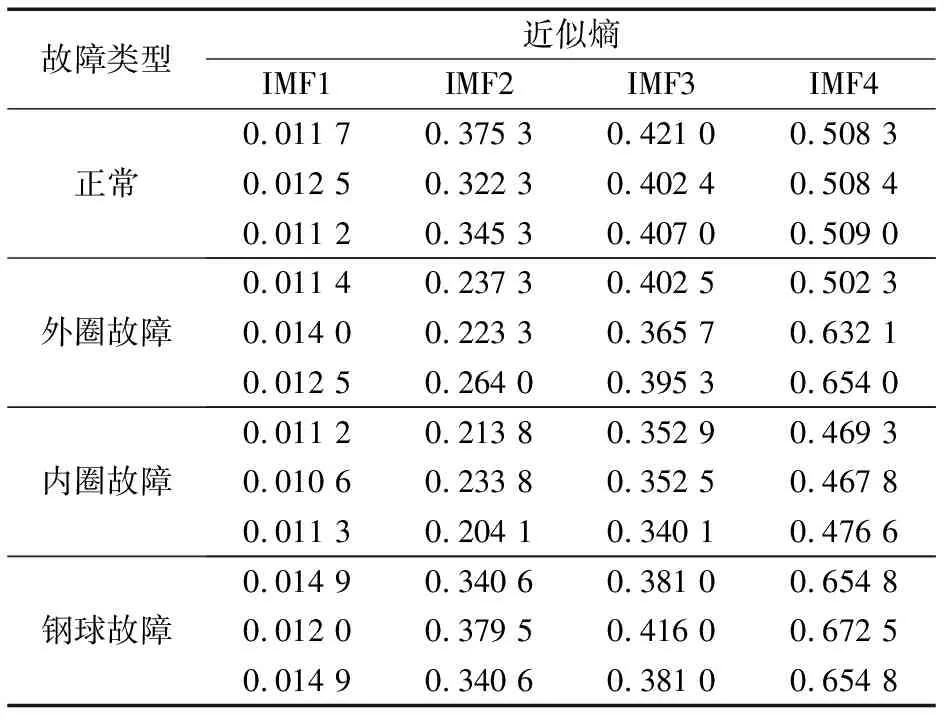
表1 不同工况下振动信号IMF分量的近似熵
分别从4种工况中随机选出25个近似熵向量,共100个组成训练样本用于训练SVM。采用5重交叉检验法,选择最优的RBF核函数参数σ=2.5和惩罚系数C=250。训练完成后对剩余的100个向量进行分类测试,为减小误差,上述试验重复10次后取其平均值,用识别率作为指标进行评价。
VMD近似熵与EMD[10]近似熵、LMD[11]近似熵经SVM处理后的分类结果见表2。由表可知:在EMD近似熵、LMD近似熵作为样本进行分类时,识别率不高,这是由于使用EMD和LMD在进行信号分解时,受伪分量和模态混叠的影响较大[12-13],分解后各分量包含的频段近似熵也会受到影响,从而降低识别率;而VMD能很好地对信号进行频段上不同尺度表征,其近似熵向量更具分类特性,易于分类器的分类,识别率也更高,更适用于滚动轴承的故障诊断。
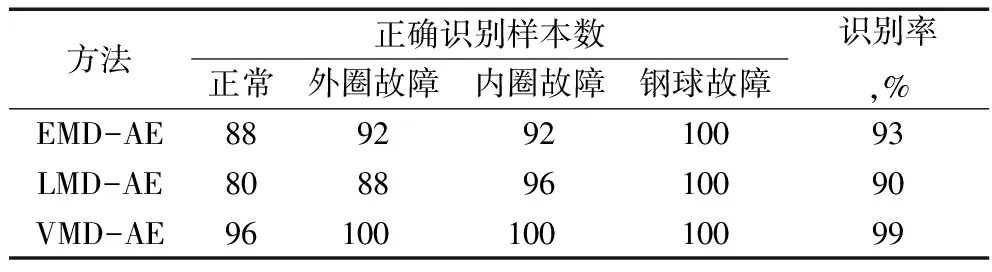
表2 不同故障诊断方法的精度
3 结束语
通过对VMD近似熵及SVM的分析,可得出如下结论:
1)VMD是一种自适应的信号处理方法,可精确地应用于非线性、非平稳信号的处理过程中,较好的在不同频带尺度下表征原信号。
2)近似熵具有很强的表征信号不规则性和复杂性的能力,VMD近似熵与SVM相结合的方法可以成功地捕捉到不同故障类型信号在不同频段尺度下变化的不规则性,对轴承的工作状态和故障类型进行辨识。
3)与EMD和LMD近似熵相比,VMD近似熵与SVM相结合的识别率更高,性能更好,可用于轴承故障的自动化诊断。
