发动机曲轴断裂分析与结构改进

蒋明安，周瑞丽，黄碧君

(台州职业技术学院 机电学院，浙江台州 318000)



发动机曲轴断裂分析与结构改进

蒋明安，周瑞丽，黄碧君

(台州职业技术学院 机电学院，浙江台州 318000)

摘要：三轮摩托车在行驶过程中经常出现曲轴断裂现象，影响了客户的使用安全及企业的声誉.采用有限元软件，对三轮摩托车发动机的曲轴进行静力分析，找到了曲轴应力最大的部位，这与实际断裂的情况吻合.对曲轴产生最大应力部位的结构参数进行改进，并对曲轴材料进行了调整，取得了较满意的结果.

关键词：曲轴；断裂分析；结构改进

三轮摩托车发动机曲轴是发动机的核心部件，它是活塞运动的连接部件，其性能的好坏将影响到发动机的使用寿命和可靠性[1].由于曲轴结构复杂，很难用传统的方法进行计算，并获得满意的结果.某三轮摩托车发动机为单缸发动机，在实际运行过程中，发动机曲轴大概在1个月内便出现了断裂，而且断裂位置相对比较稳定.因此，本文主要通过有限元方法，对曲轴断裂进行分析，以期为实际生产提供理论依据.

1有限元模型的建立

为了更加接近于实际，在CAD建模时，曲轴所有倒圆角、倒角部分均未简化，按照原始尺寸进行建模，同时忽略油孔部分.

使用UG软件对曲轴进行CAD建模，然后导入有限元分析软件ANSYS中，对三轮摩托车发动机的曲轴进行静力学分析，采用SOLID95单元，设置单元边线长度为4 mm，进行网格划分，结果如图1所示.

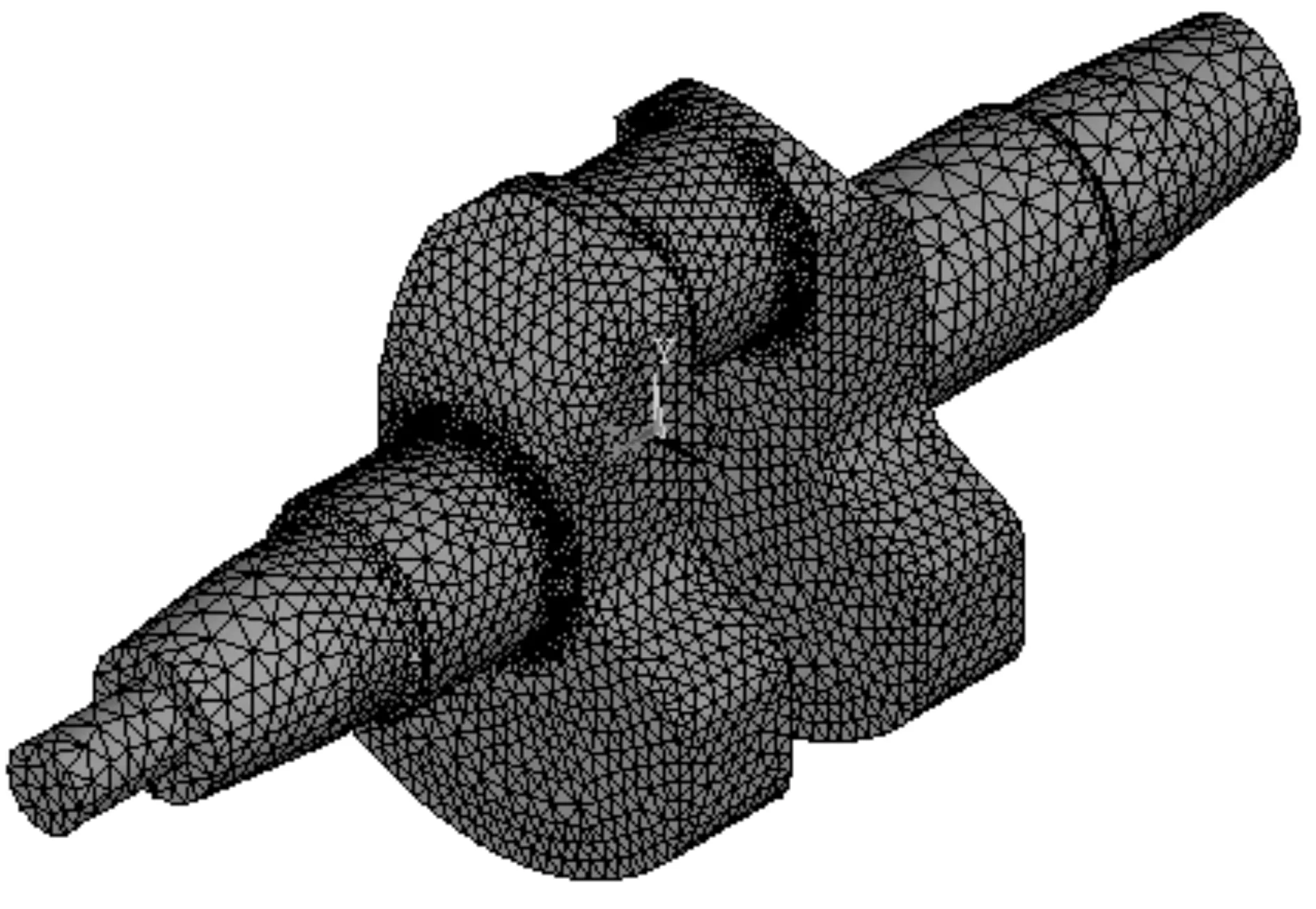
图1　曲轴的网格划分

发动机的主要分析参数如下：额定功率为5.5 kW；额定转速为3 000 r/min；分析的曲轴为单拐曲轴，总长为287.3±0.3 mm；与发动机连杆相连的轴颈尺寸为40 mm；曲轴的曲柄半径为35 mm；连杆质量为0.78 kg；连杆中心距为116 mm；活塞组质量为0.45 kg；活塞直径为88 mm；曲轴材料为QT600-2；材料密度为7 120 kg/m3；弹性模量为169 GPa；泊松比为0.286；抗拉强度为600 MPa，屈服强度为330 MPa.

根据文献[2]和[3]可知，施加在活塞上的气体作用力为：

(1)

式中：D为活塞直径；p为燃烧室内气体的压力，可通过示功图来获得.

活塞和连杆的往复惯性力为：

Fw=-mwrw2(cos(α)+λcos(2α))

(2)

式中：mw为连杆和活塞组件的往复运动质量；r为曲柄半径；w为曲柄旋转角速度；α为曲柄旋转角度；λ为曲柄半径r与连杆中心距L的比值.

因此，连杆作用力F的计算公式为：

F=(Fp+Fw)/cos(β)

(3)

式中，β为连杆的旋转角度.

根据式(1)～(3)可求出，曲轴所受的最大压缩载荷在发动机膨胀冲程的上止点附近，其值为116 117 N，而最大拉载荷在发动机进气冲程的上止点附近，其值为5 525 N.假设载荷沿圆周和轴线方向为二次抛物线分布，加载到轴颈部位[2].

设置曲轴左端轴承安装处(采用6308的轴承)径向约束条件为0(以圆柱坐标进行设置)，而在曲轴的右端，即输出扭矩的一端，设置θ和z的约束条件为0.考虑到曲轴自身惯性力的影响，设置额定转速3 000 r/min时的角速度为314 rad/s，加速度为9.8 m/s2.

2仿真与结果讨论

2.1原曲轴强度分析

图2、图3分别为受压和受拉载荷下，原曲轴的Vom Mises等效应力云图.从图中可以看出，应力最大的位置均在轴颈和右端曲柄臂相连的过渡圆角下部，其值分别为346 MPa、8.08 MPa.在受压载荷下，曲轴所承受的应力要大于材料的屈服强度，容易导致曲轴材料破坏，产生断裂.

图2　原曲轴受压的Vom Mises等效应力云图

三轮摩托车在实际运行中，发动机曲轴出现了断裂，而且断裂的位置相对比较稳定，均为图4中位置.这与有限元计算的结果(图2)完全一致，表明曲轴主要是受到压载荷作用才导致断裂的.

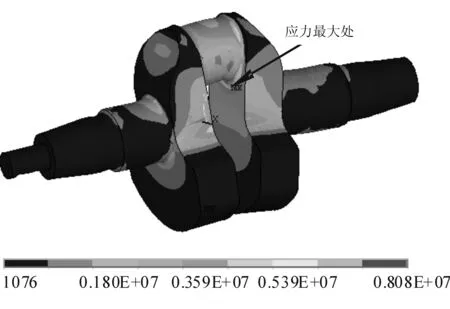
图3　原曲轴受拉的Vom Mises等效应力云图

图4　曲轴断裂实物图

图5　曲轴结构示意图

2.2改进曲轴强度分析

从以上分析可知，曲轴强度未达到要求.为了提高强度，对图5所示的三个结构参数进行修改.将原始尺寸D=40 mm，B=48 mm，R0=2.5 mm改为D=50 mm，B=60 mm，R0=4.5 mm，同时为了修改后，曲轴不产生附加偏心力，笔者将曲柄臂的配重重新调整.同时将材料改为QT800-2，它的密度为7 300 kg/m3，弹性模量为174 GPa，泊松比为0.27，抗拉强度为800 MPa，屈服强度为480 MPa.

图6为受到最大压缩载荷时，改进曲轴的Vom Mises等效应力云图.图7为受到拉载荷时，改进曲轴的Vom Mises等效应力云图.从图中可以看出，应力最大的位置仍然在轴颈和右端曲柄臂相连的过渡圆角下部，但压应力要比拉应力大很多，分别为198 MPa、5.77 MPa，应力均小于材料的屈服强度480 MPa.但还需进一步对其进行疲劳强度校核.

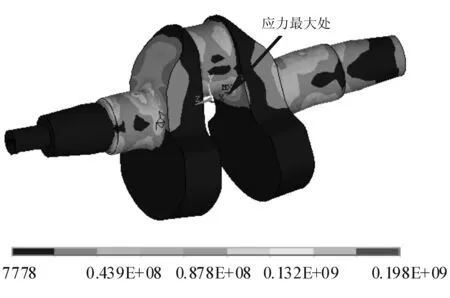
图6　改进曲轴受压的Vom Mises等效应力云图

图7　改进曲轴受拉的Vom Mises等效应力云图

在工程设计中，曲轴疲劳强度校核通常采用Goodman直线或折线方程的疲劳安全系数进行评价，计算公式如下[4-5]：

nσ=δ-1/(kσδa/(εσβσ)+Ψσδm)

(4)

式中：δ-1为对称疲劳极限，取值为360 MPa；kσ为应力集中系数，取值为1；εσ为尺寸系数，取值为0.84；βσ为强度系数，取值为1.4；Ψσ为不对称敏感系数，取值为0.36.以上数据均由文献[5]提供.δa为应力幅，可通过图6、图7的应力云图得到，其值为(198-5.77)/2=96.12 MPa.δm为平均应力，其值为(198+5.77)/2=101.89 MPa.

通过式(4)，便可得到疲劳安全系数，表1为曲轴结构改进前后的对比数据.从表中可以看出，曲轴改进后，最大Vom Mises等效应力值明显下降，疲劳安全系数明显提高，而且其值大于1.8，满足设计要求，属于安全的.图8为改进后的曲轴实物图.

表1　曲轴改进后对比数据

图8　改进后的曲轴

3结论

通过有限元软件对三轮摩托车发动机的曲轴进行受力分析，可以得到以下结论：(1)曲轴断裂主要是由于发动机在膨胀冲程的上止点附近，受到压载荷的作用，产生的应力值大于材料的屈服强度，导致曲轴材料破坏，出现断裂现象；(2)通过增加曲轴直径、曲颈和曲柄臂相连的过渡圆角值，选择更好的曲轴材料，可以有效减少曲轴工作时产生的应力.通过疲劳强度校核，此方案是可行的，改良后的曲轴完全满足疲劳强度的设计要求.

参考文献:

[1]王晓华,崔志琴,张腾,等. 汽车发动机曲轴的参数化设计[J]. 农业装备与车辆工程,2011(12):43-45.

[2]蒋明安,王金生. 有限元方法在发动机曲轴断裂分析的应用[J].机械工程师, 2013(12):163-164.

[3]黄以兵. 16V17柴油机曲轴研制与有限元分析[D].山东理工大学,2012.

[4]邓召文,陈涛. 基于ANSYS的BN492发动机曲轴有限元分析[J].农业装备与车辆工程,2010(8):29-33.

[5]刘必荣. 基于ANSYS的小型柴油机曲轴应力分析[J].拖拉机与农用运输车,2004 (3):30-32.

收稿日期：2015-11-16

基金项目：台州市科技计划资助项目(14GY06)

作者简介：蒋明安 (1963-)，男，浙江台州人，高级工程师，主要研究方向为机械设计与制造工艺.

文章编号：1006-3269(2016)02-0034-03

中图分类号：TG385.2; TG316

文献标识码：A

doi:10.3969/j.issn.1006-3269.2016.02.008

Fracture Analysis and Structural Improvements of the Engine Crankshaft

JIANG Ming-an，ZHOU Rui-li，HUANG Bi-jun

(Taizhou Vocational and Technical College, Taizhou 318000,China)

Abstract：The fracture of the three wheeled motorcycles crankshafts greatly affects customers use and corporate reputation. This paper carries out the static analysis of engine crankshaft by the finite element software, and found out the fracture position which is consistent with the actual fracture position. Crankshaft structural parameters of the fracture position have been modified and the material has been adjusted which reaches a satisfied result.

Key words:crankshaft；fracture；structural improvement