天文潮与海啸耦合数学模型研究
——以东中国海温州湾为例
2016-07-26孙志林
赵 鑫,应 超,孙志林
(1.浙江大学 海洋学院,浙江 杭州 310058;2.浙江省水利河口研究院 浙江 杭州 310020)
天文潮与海啸耦合数学模型研究
——以东中国海温州湾为例
赵鑫1,2,应超2,孙志林*1
(1.浙江大学 海洋学院,浙江 杭州 310058;2.浙江省水利河口研究院 浙江 杭州 310020)
摘要:在COMCOT海啸数学模型中加入潮汐边界条件,建立了东中国海天文潮与海啸耦合数学模型。在琉球海沟内侧设计震级为7.6级的海底地震,根据地震板块的错动方向不同,设计正波先行与负波先行两种海啸波,通过调整海啸波发生时间,使海啸波波峰遭遇温州湾天文高潮位。将天文潮与海啸耦合模型计算结果与线性叠加计算结果进行比较,结果表明:无论正波先行还是负波先行,天文潮与海啸耦合计算相比线性叠加的结果,海啸波的到达时间均有所提前;而从海啸波波高来看,线性叠加的计算结果则比耦合计算结果偏高。
关键词:COMCOT模型;天文潮;海啸;耦合计算;线性叠加
0引言
海啸是最为恶劣的海洋灾害之一,一旦形成破坏力极大。准确的海啸预报是最大化减轻海啸灾害的前提条件,而海啸数值模拟是海啸预报的重要手段。现有的海啸计算模式中,一般都不含有潮汐模块,通常不考虑潮汐与海啸的非线性作用,将计算出的海啸波高与潮位值进行线性叠加,来得到关心站点的水位。但是,在近岸浅水域,潮汐与海啸的非线性作用会明显增大,线性叠加潮位与海啸波的预报方法,显然存在一定误差。
关于海啸波与天文潮的耦合,国内外已经有丰硕的研究成果。WEISZ和WINTER[1]研究表明潮汐引起的水深变化在海啸爬高计算时不可忽略。KOWALIK et al[2]通过简单一维模型来考查潮汐与海啸的非线性作用,分别设置不同宽度的陆架地形进行研究,结果显示,在较窄的陆架上传播时海啸与潮汐的相互作用短暂,主要表现在爬高中对海啸流的影响;在较宽的陆架上传播时,由于底摩擦的影响,海啸波幅和流减小,而潮汐水位和流的大小几乎保持不变。DAO et al[3]模拟2004 年印度洋大海啸事件时,考虑潮汐引起的水位变化,分析比较了在高、低潮位时泰国和马来西亚等沿岸海啸波高大小及到达时间,结果差异显著。姚远 等[4]应用建立在潮汐背景上的HAMSOM 模式,对1994年发生在台湾海峡的一次海啸事件进行了模拟。本文建立了东中国海天文潮与海啸耦合数学模型,分析了天文潮与海啸耦合计算所得的海啸到达时间、近岸海啸波高和两者线性叠加计算结果的区别。
1数学模型建立与验证
1.1COMCOT模型介绍
COMCOT[5](Cornell Multi-grid Coupled Tsunami model)模式是由 Cornell 大学 Liu PL-F 开发的基于浅水长波方程的海啸数值计算模式,能够有效模拟海啸发生、传播和淹没的全过程。模式提供选择在球面坐标或笛卡尔直角坐标系统下求解线性或非线性长波方程,并可设置多重嵌套网格,兼顾了计算精度和计算效率。基本方程如下:
(1)
(2)
式中:η为相对于平均海平面的自由表面位移,P为沿纬度单位宽度的通量,Q为沿经度单位宽度的通量,φ和ψ分别为经度和纬度,f为科氏力系数,g为重力加速度,R为地球半径,H为水深,t为时间。海啸传播至近岸,采用笛卡尔坐标下非线性浅水波方程,并考虑底摩擦效应,其连续方程和动量方程如下:
(3)
(4)
(5)
式中:P和Q分别为x和y方向上的体积通量,n为曼宁粗糙系数。
COMCOT模式已被多次用来模拟历史海啸事件,如1992年Flores Islands(印度尼西亚)海啸[6],2003年Algeria海啸[7]以及2004年印度洋大海啸[8]。李林燕 等[9]将其应用于南海海域的海啸传播计算并取得了良好的效果;应超 等[10]采用该模型对日本“3·11”海啸进行了验证,证明了其在东中国海的适用性。
1.2天文潮模型建立与验证
COMCOT模型采用长波浅水方程,同样可以用来描述潮波的运动。本文在COMCOT模型中加入潮汐边界条件,使其可以模拟东海潮波。外海潮位边界由全球潮汐模型(TPXO7)求得,该模型通过10个分潮推算天文潮位,包含8个主要分潮M2、S2、K1、O1、N2、P1、K2和Q1,以及2个长周期分潮Mf和Mn,基本能够构造出外海深水处真实的天文潮过程:

(6)
式中:ζ0为边界处的潮位;ζp为边界处静压水位;i等于1至10,分别对应上述分潮;Ai和αi分别为分潮在3条边界处的振幅和迟角;ωi为分潮的角频率。
天文潮计算范围约为15 °38′~41°47′N,111°56′~135°32′E,共分4重网格,首重网格尺度为2o,第2重网格尺度为1 800 m,第3重网格尺度为600 m,第4重网格尺度为200 m,网格布置如图1所示。

图1 天文潮计算网格布置图Fig.1 The layout of computational grids for astronomical tide
首层网格地形数据采用ETOPO1数据,其余网格地形数据采用海图与实测地形插值得到。采用2013年4月温州湾洞头、南麂的实测潮位资料对天文潮模型进行验证,同时在铜盘山与霓屿岛连线布置一个监测点A(27°45′58.38″N,120°57′49.73″E),验证潮位站与监测点分布见图2,各潮位站验证图见图3。由验证图可见,计算潮位与实测潮位无论是相位还是大小都吻合良好,证明了加入潮汐边界的COMCOT模型可以应用于天文潮波的模拟。

图3 天文潮位验证Fig.3 The verification of astronomical tide
2海啸震源设计
为使海啸波往温州海域传播且尽量不影响天文潮边界,海啸震源设计在图1中琉球海沟位置内侧,参考太平洋海啸预警中心的7.5级以上即发布海啸预警公告的规定,设计震级定为7.6级。地震板块的错动方向不同,海啸波可分为正波先行与负波先行两种,设计震源参数见表1,包括震中经度(LON)、震中纬度(LAT)、震源深度(DEP)、断裂面长度(L)、断裂面宽度(W)、倾角(DIP)、走向角(STRIKE)、滑移角(SLIP)和滑移距离(SLIP DIS)。采用图1所示的网格进行纯海啸波计算,正波先行海啸的初始水面波动和最大增水见图4,负波先行海啸的初始水面波动和最大增水见图5。

表1 设计海啸震源参数

图4 设计正波先行海啸初始水面(a)和最大增水(b)Fig.4 The initial water level(a) and maximum set-up(b) of designed tsunami for positive leading wave
提取图2中监测点A在海啸过程中的水面波动过程线见图6。由图6可见,负波先行时监测点A在海啸波来临时水面先略有下降,然后迅速抬升,正波先行时监测点A在海啸波来临时水面先略有抬升,震荡一下后再迅速抬升。负波先行时,纯海啸情况下A点最大增水为0.23 m,发生在地震后3 h 50 min;正波先行时,纯海啸情况下A点最大增水为0.22 m,发生在地震后4 h 15 min。
3天文潮与海啸耦合计算
在天文潮计算稳定的基础上,通过调整海啸波发生时间,使海啸波波峰遭遇温州湾天文高潮位。天文潮耦合正波先行海啸波时海啸发生后各时刻水位图见图7,天文潮耦合负波先行海啸波时海啸发生后各时刻水位图见图8。由图可以看出,设计海啸波会扰乱原有天文潮系统,形成狭长状冲击波向近岸传播。
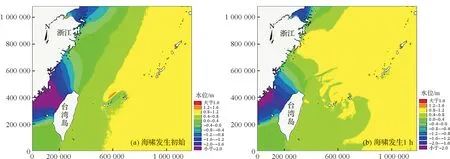
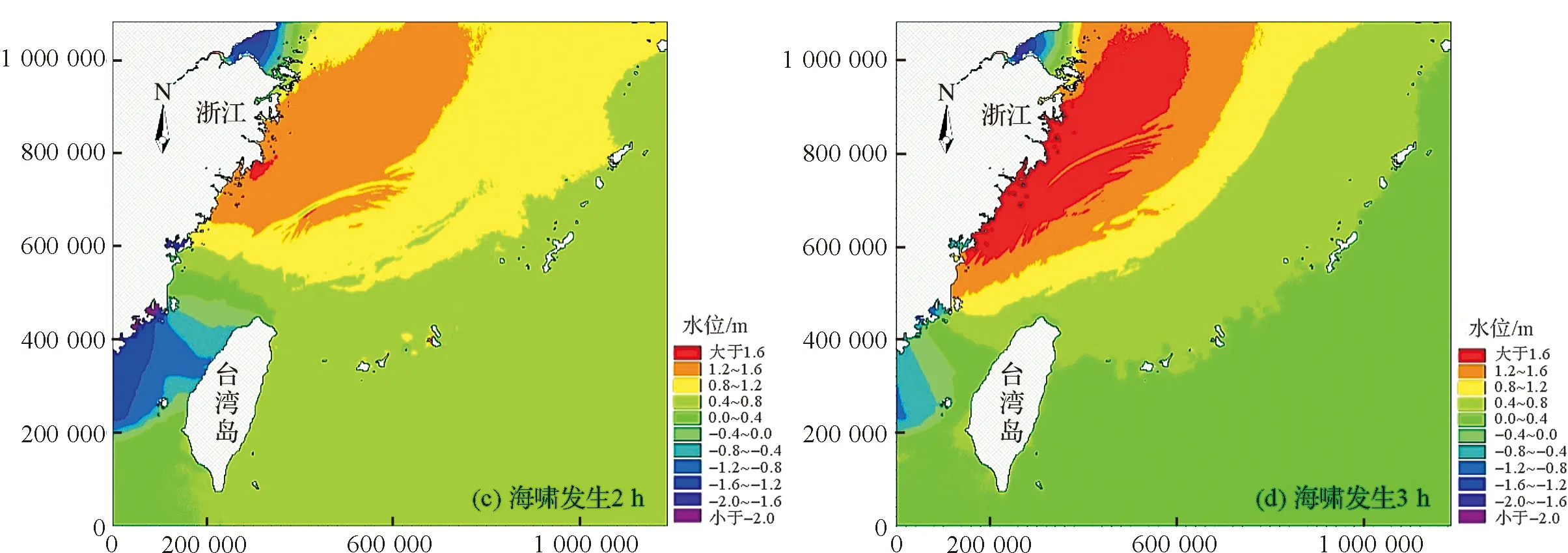
图7 天文潮海啸耦合计算海啸水位图(正波先行)Fig.7 Water level contour of the coupled astronomical tide and tsunami model (positive leading wave)
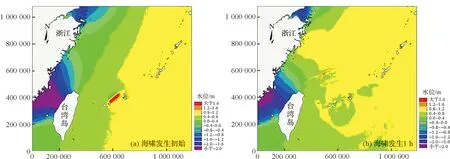
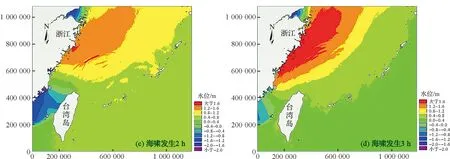
图8 天文潮海啸耦合计算海啸水位图(负波先行)Fig.8 Water level contour of the coupled astronomical tide and tsunami model (negative leading wave)
统计监测点A在耦合计算与线性叠加情况下的潮位过程线见图9。由图可见,受海啸波影响,天文潮潮位曲线会产生高频微小波动。天文潮与海啸耦合计算相比线性叠加的结果,海啸波的到达时间均有所提前,提前约10 min左右。这与理论分析是一致的,海啸波的速度近似为(gH)1/2,当海啸波与高潮位重合时,耦合计算总水深H增大,海啸传播速度增大,传播时间变短。而从海啸波波高来看,线性叠加的结果则比耦合计算结果偏大,最高偏大12 cm左右。这说明线性叠加对海啸波高的预报结果是偏安全的。
4结语
本研究在COMCOT海啸数学模型中加入潮汐边界条件,建立了东中国海天文潮与海啸耦合数学模型。通过在琉球群岛设计震级为7.6级的海底震源,生成正波先行与负波先行两种海啸波,通过调整海啸发生时间使海啸波波峰遭遇温州湾天文潮高潮位。以监测点A为例分析了天文潮和海啸耦合计算结果与两者线性叠加计算结果的区别,计算结果表明,无论是正波先行海啸还是负波先行海啸遭遇天文高潮位时,耦合模型计算所得到达时间均提前于线性叠加计算结果,而耦合模型计算的海啸波高则略小于线性叠加计算结果。

图9 监测点A的潮位过程线Fig.9 Tide level time series of monitoring point A
参考文献(References):
[1] WEISZ R, WINTER C. Tsunami, tides and run-up: a numerical study[C]//PAPADONPOULOS G A, SATAKE K. Proceedings of the International Tsunami Symposium,Chania, Greece.2005,322:27-29.
[2] KOWALIK Z, PROSHUTINSKY T, PROSHUTINSKY A. Tide-tsunami interactions[J]. Science of Tsunami Hazards,2006,24(4):242-256.
[3] DAO M H, TKALICH P. Tsunami propagation modelling? a sensitivity study[J]. Natural Hazards and Earth System Science,2007,7(6):741-754.
[4] YAO Yuan, CAI Shu-qun, WANG Sheng-an. Preliminary numerical simulation of a tsunami in Taiwan Strait[J]. Journal of Tropical Oceanography,2009,28(2):1-6.
姚远,蔡树群,王盛安.台湾海峡一次海啸的初步数值模拟[J].热带海洋学报,2009,28(2):1-6.
[5] PAN Wen-liang,WANG Sheng-an. Introduction and application of COMCOT model[J].Marine Forecasts, 2009,26(3):45-52.
潘文亮,王盛安.COMCOT数值模式的介绍和应用[J].海洋预报,2009,26(3):45-52.
[6] LIUP L F, CHO Y S, BRIGGS M J, et al. Runup of solitary waves on a circular Island[J]. Journal of Fluid Mechanics,1995,302(9):259-285.
[7] WANG X, LIU P L F. A numerical investigation of Boumerdes-Zemmouri (Algeria) earthquake and tsunami[J]. Computer Modeling in Engineering and Science,2005,10(2):171-183.
[8] WANG X, LIU P L F. An analysis of 2004 Sumatra earthquake fault plane mechanisms and Indian Ocean tsunami[J]. Journal of Hydraulic Research,2006,44(2):147-154.
[9] LI Lin-yan, MAO Xian-zhong.Numerical study for tide-tsunami coupling model in Shenzhen waters[J]. Acta Oceanologica Sinica,2012,34(3):11-18.
李林燕,毛献忠.深圳海域潮汐海啸波耦合数值研究[J].海洋学报,2012,34(3):11-18.
[10] YING Chao,YU Pu-bing, MU Jin-bin, et al.Study on inversion forecasting model for East China Sea——A case study of Japan "3·11" tsunami[J]. Marine Forecasts,2015,32(3):36-42.
应超,于普兵,穆锦斌,等.东海海啸反问题预报模式研究——以日本“3·11”海啸为例[J].海洋预报,2015,32(3):36-42.
收稿日期:2016-02-23修回日期:2016-04-10
基金项目:浙江省自然科学基金项目资助(LY13E090001);浙江省科技计划项目资助(2015F50064,2015F50011)
作者简介:赵鑫(1978-),男,浙江上虞市人,高级工程师,主要从事海洋水动力数值模拟研究。E-mail:zhaox@zjwater.gov.cn *通讯作者:孙志林(1956-),男,教授,主要从事水沙动力学及河口海岸数值模拟研究。E-mail:oceansun@zju.edu.cn
中图分类号:P731.36
文献标识码:A
文章编号:1001-909X(2016)02-0011-07
Doi:10.3969/j.issn.1001-909X.2016.02.002
Research on astronomical tide and tsunami coupled numerical model——A case study of Wenzhou Bay,East China Sea
ZHAO Xin1,2, YING Chao2, SUN Zhi-lin*1
(1.OceanCollege,ZhejiangUniversity,Hangzhou310058,China; 2.ZhejiangInstituteofHydraulics&Estuary,Hangzhou310020,China)
Abstract:An astronomical tide and tsunami coupled numerical model of East China Sea was established by adding tidal boundary conditions into COMCOT tsunami model. Two different tsunami waves, positive leading wave and negative leading wave, were designed according to the dislocation direction of earthquake plates during an undersea earthquake with magnitude of 7.6, which occurred in Ryukyu Trench. The tsunami wave crest and astronomic high tide level occurred at the same time through the modification the phase of tsunami wave. Comparison about the summation of astronomic tide level and tsunami wave level was made between the result of coupling model and linear sum. It demonstrates that in both cases mentioned above, the tsunami wave is in advance no matter for the positive leading wave or negative leading wave. And it’s higher for the result of linear sum with respect to tsunami wave height.
Key words:COMCOT model; astronomical tide; tsunami; coupling model; linear sum
赵鑫,应超,孙志林.天文潮与海啸耦合数学模型研究——以东中国海温州湾为例[J].海洋学研究,2016,34(2):11-17,doi:10.3969/j.issn.1001-909X.2016.02.002.
ZHAO Xin, YING Chao, SUN Zhi-lin. Research on astronomical tide and tsunami coupled numerical model——A case study of Wenzhou Bay, East China Sea[J]. Journal of Marine Sciences, 2016,34(2):11-17, doi:10.3969/j.issn.1001-909X.2016.02.002.
