消声器传递损失预测的边界元数值配点混合方法

杨　亮， 季振林， Wu T W

(1.哈尔滨工程大学 动力与能源工程学院，哈尔滨　150001；2.肯塔基大学 机械工程学院，列克星敦　40506)



消声器传递损失预测的边界元数值配点混合方法

杨亮1， 季振林1， Wu T W2

(1.哈尔滨工程大学 动力与能源工程学院，哈尔滨150001；2.肯塔基大学 机械工程学院，列克星敦40506)

摘要：将边界元法与数值配点法结合形成混合方法用于计算任意截面形状消声器的传递损失。消声器划分为若干子结构，用边界元法计算具有非规则形状的子结构阻抗矩阵，用二维有限元法提取等截面子结构特征值及特征向量，用配点法获得阻抗矩阵；将每个子结构阻抗矩阵连接用于传递损失计算。为减少计算时间提出简化方法计算消声器传递损失。结果表明，混合法在保证计算精度前提下可节省计算时间。

关键词：消声器；传递损失；边界元方法；数值配点方法

解析方法、数值方法广泛用于消声器传递损失计算。前者虽计算速度快、精度高，但只能用于规则形状消声器计算，Selamet等[1-3]用解析模态匹配法计算膨胀腔、内插管膨胀腔及回流腔等消声器传递损失。Selamet等[4]用二维解析模态匹配法计算填充吸声材料的阻性消声器声学性能。数值方法适用性强，理论上可用于任意复杂结构消声器计算，Peat等[5]用有限元、Ji[6]用边界元、Wu等[7-8]用直接混体边界元法对不同类型消声器进行广泛研究。其中，直接混体边界元法更具灵活性，尤其适用消声器的声学性能计算。对大尺度问题，数值方法计算时间长、内存需求大。因此，考虑将解析法与数值法结合用于消声器声学性能研究具有实际意义。Kirby等[9-12]用二维有限元法获得消声器或空调管道截面的特征值及特征函数，用配点法获得相关声学性能评价参数，并用数值模态匹配法对阻性消声器进行研究。Fang等[13-14]用数值模态匹配法对抗性消声器及有流穿孔阻性消声器进行计算。

无论数值配点法或数值模态匹配法，对沿轴向方向消声器或消声管道截面形状变化情况均不适用，因此，不同计算方法的耦合及优化需进一步研究。

本文拟用边界元-数值配点混合法进行消声器传递损失计算。将消声器划分为若干子结构，对沿轴向管道截面变化或具有复杂内部结构的子结构用直接混体边界元法计算其阻抗矩阵，考虑三维边界元法与二维有限元法网格划分的一致性，对截面均匀一致的子结构考虑用二维有限元方法进行特征值分析，获得横向波数，进而用配点法计算获得阻抗矩阵，将不同子结构阻抗矩阵连接获得消声器的传递损失。为减少计算时间，用简化方法压缩子结构阻抗矩阵，并通过算例验证混合方法的有效性。

1直接混体边界元方法

该方法源于传统子结构边界元方法，即将具有复杂内部结构的消声器分成若干具有明确边界的几部分，对每部分用边界积分方程描述，据各部分交界面的声学参数连续条件获得整体控制方程。交界面有两个未知量时，用超奇异积分方程提供额外方程。本文涉及的边界积分方程(完整积分见文献[8])为

(1)

(2)

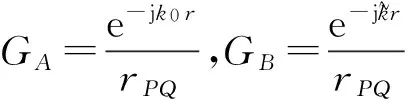
图1　消声器子结构划分Fig.1 Substructure division of silencer

源点、场点距离较近时，对公式中涉及的奇异积分及超奇异积分需妥善处理[15-16]。不同于文献[7-8]求解矩阵的直接方法，本文用带预处理的BI-CG求解器。为描述问题，将消声器分三部分(图1)，对子结构A、C，考虑用边界元方法获得阻抗矩阵；对子结构A，阻抗矩阵可表示为

(3)

式中：PAI，vAI分别为进口声压及质点振速向量；PAO，vAO分别为出口声压及质点振速向量。

阻抗矩阵作为结构声学特性描述，是唯一确定的。对式(3)需在不同边界条件下用BEM计算。如，为获得阻抗矩阵第一列数值，对进口第一单元设v=1，进出口其它单元设v=0，进出口声压值即为第一列阻抗矩阵值。尽管需多次运行BEM，但每次求解的矩阵相同。对结构C，得阻抗矩阵为

(4)

2数值配点法

图1的子结构B沿轴向等截面，但由于截面形状任意，无法用解析法获得横向波数，故用数值方法进行特征值分析，考虑二维有限元及三维边界元网格划分的一致性，为便于各子结构阻抗矩阵连接，用二维有限元计算特征值及特征向量。以阻性穿孔管道为例，图1中Ⅰ的内部为空气，Ⅱ为填充吸声材料，Ⅰ与Ⅱ之间由穿孔管分隔。区域Ⅰ、Ⅱ内横向声压控制方程可表示为

(5)

(6)

式中：pxy1，pxy2分别为区域Ⅰ、Ⅱ的横向声压分量；kxy1，kxy2分别为空气、吸声材料中横向波数，两区域轴向波数kz相同，与横向波数满足关系为

(7)

(8)

穿孔管内外满足边界条件为

(9)

用伽辽金加权余量法并代入边界条件获得阻性穿孔管道横截面的本征方程[17]为

(10)

(11)

(12)

求解式(10)可获得轴向波数及本征向量Φn(x,y)。对穿孔管抗性消声器，式(10)简化[18]为

(13)

对刚性壁直管道，横截面本征方程表达式为

(14)

管道内声压、质点振速表示为

(15)

(16)

(17)

在B的进出口各选N个配点，则有N个模态，据式(16)，获得B进出口配点振速为

(18)

同理，据式(15)得进出口声压表达式为

(19)

3消声器传递损失计算

若使子结构B进出口配点分别与子结构A的出口截面、子结构C的进口截面节点一致，可连接二者阻抗矩阵获得整体阻抗矩阵用于传递损失计算。对图1消声器，按结构连接顺序，建立前两子结构A、B进出口阻抗矩阵关系，即

(20)

式中：

用相同方法，将式(20)中阻抗矩阵与子结构C的阻抗矩阵连接可得整个结构进出口的阻抗矩阵关系，即

(21)

对含更多子结构的消声器，阻抗矩阵计算方法相同。在消声器进出口，声波可视为平面波，此时式(21)被压缩为2×2的矩阵。消声器四极参数表示为

(22)

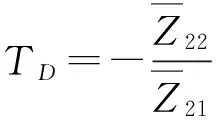
传递损失计算公式可表示为

(23)

式中：SI，SO分别为消声器进出口面积。

4算例验证

以一方形膨胀腔消声器为例验证本文方法的正确性，见图2。将消声器划分为3个子结构，lA=lC=0.05 m，lB=0.125 m，进出口管道长宽均b=0.05 m，膨胀腔长宽均bc=0.15 m。子结构A、C的阻抗矩阵由BEM获得，子结构B的阻抗矩阵由配点法计算，各子结构交界面均生成144个单元，即可考虑144个模态，计算结果见图3。由图3看出，混合方法计算结果与三维边界元吻合较好，该方法的正确性获得验证。用数值配点方法计算阻抗矩阵，只需在子结构进出口划分网格，可节省计算时间，该时间与子结构长度无关，适用于具有较长等截面结构的大尺度声学问题。需注意的是，由于横向波数及本征向量由二维有限元方法获得，较解析方法相比存在一定误差，且随模态阶数提高误差有增大趋势。据文献[9],本算例认为最高到第29个模态结果较准确，其后高阶模态对应的特征值、特征向量与准确值误差较大。因高阶模态对结果贡献量小，故传递损失计算结果相对准确，解析法与数值法对前5个高阶模态计算结果比较见表1。

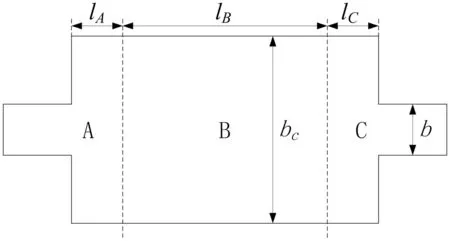
图2　方形膨胀腔消声器Fig.2 Square expansion chamber silencer

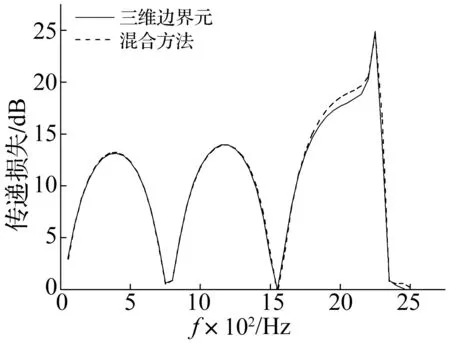
图3　方形膨胀腔消声器传递损失Fig.3 TL of square expansion chamber silencer

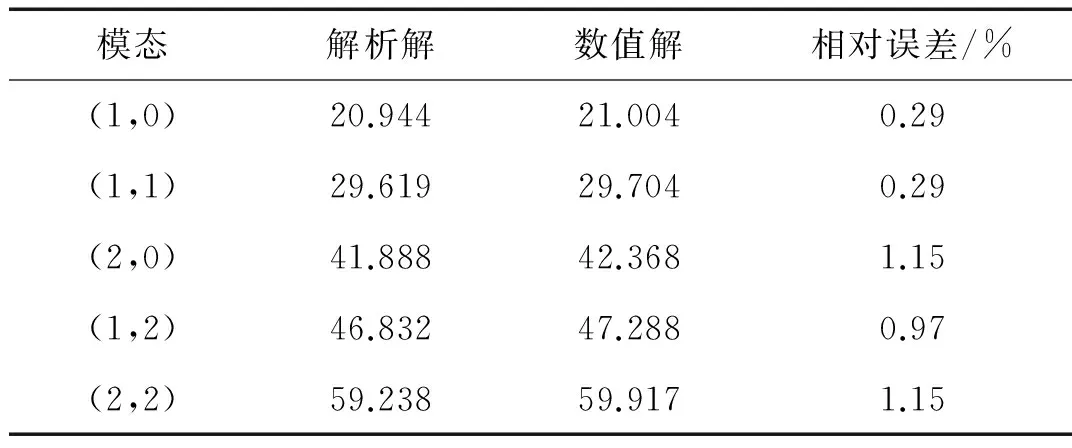
模态解析解数值解相对误差/%(1,0)20.94421.0040.29(1,1)29.61929.7040.29(2,0)41.88842.3681.15(1,2)46.83247.2880.97(2,2)59.23859.9171.15

若模型尺寸较大，为保证与子结构A、C截面网格一致，B截面会划分较多网格，对式(18)、(19)，求解模态幅值系数会费较多计算时间，实际应用中，考虑过多模态无意义。本算例计算频率最高到2 500 Hz，(3,0)模态或(0,3)模态激发频率约3 440 Hz，实际计算中考虑最高到第二阶模态即可满足需要。

因此，如何保证计算精度的同时控制模态数量尚待进一步研究。本文考虑压缩子结构A、C的阻抗矩阵，在A的出口截面及C的进口截面划分若干子区域，用区域内部节点平均声学变量近似表示整个区域声学变量数值，对子结构B的进出口截面，选择与子结构A、C划分子区域中心对应的配点，进而用数值配点法计算阻抗矩阵。子结构A进口及C出口认为平面波传播，只划分1个子区域。

以方形穿孔管抗性消声器为例，验证简化方法的正确性。图4的结构尺寸与图2相同，区别为膨胀腔内部添加穿孔管，穿孔率φ=0.08，穿孔孔径dh=0.002 49 m，穿孔壁厚tw=0.000 9 m。子结构交界面区域简化划分见图5，各子结构交界面划分为9个子区域，bs= 1/3bc=0.05 m。简化后式(3)、(4)中矩阵规模减小为10×10。对子结构B，选择与子区域1～9中心一致的配点，阻抗矩阵计算同前，式(17)中矩阵规模减小为18×18，大大减少计算时间。传递损失计算结果见图6，可见与三维边界元吻合良好，验证所提方法实际应用的有效性。

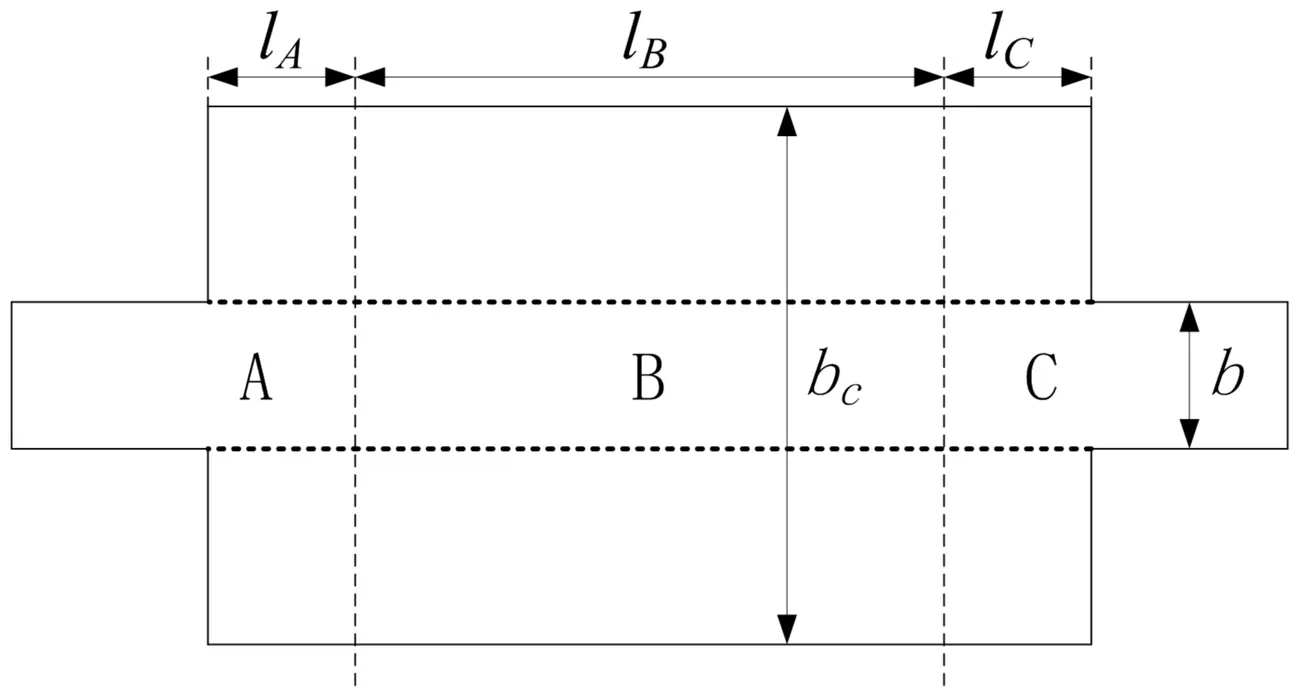
图4　方形穿孔管消声器结构尺寸Fig.4 Structure dimension of square perforated tube silencer

图5　子结构A、C截面划分Fig.5 Cross-section division of substructures A and C

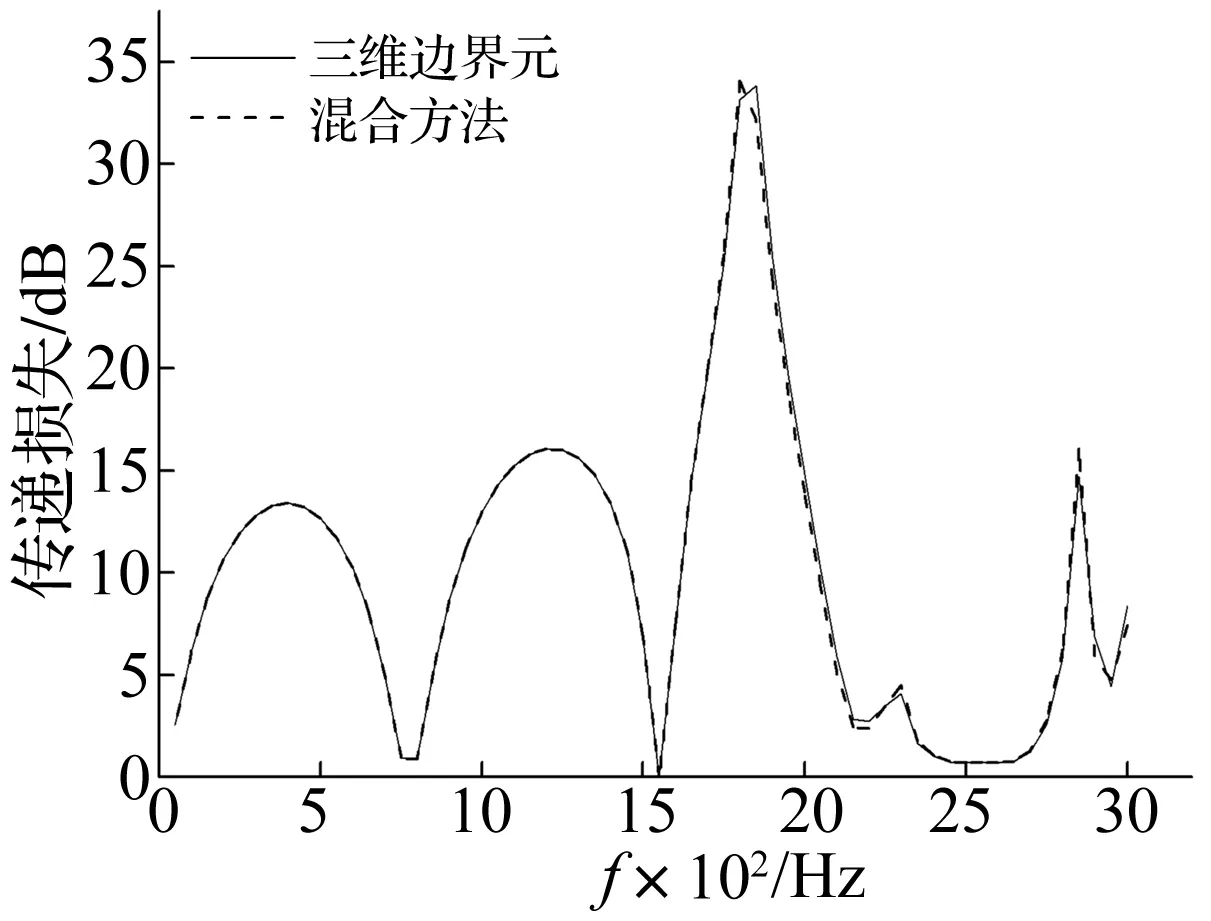
图6　方形穿孔管消声器传递损失Fig.6 TL of square perforated tube silencer

通过两个算例验证所提方法的有效性，并与传统子结构方法计算时间比较，说明本文方法的优越性。考虑穿孔管阻性消声器，模型结构尺寸同图4，区别为膨胀腔内填充吸声材料，流阻率R=4 896 Rayls/m。子结构划分形式与交界面子区域划分同图5，简化的混合方法与三维边界元计算结果见图7，可见吻合良好。

图7　方形穿孔管阻性消声器传递损失Fig.7 TL of square dissipative perforated tube silencer

椭圆截面消声器亦广泛应用，故以椭圆膨胀腔消声器为例说明简化混合方法的应用。模型尺寸见图8，lA=lC=0.05 m，lB=0.182 3 m，椭圆长轴b1=0.2 m，短轴b2=0.14 m，进出口插管长l1=l2=0.025 m，消声器进出口管道截面为圆形，半径r=0.025 m。各子结构交界面子区域划分见图9，传递损失计算结果见图10，可见计算结果与三维边界元吻合良好。

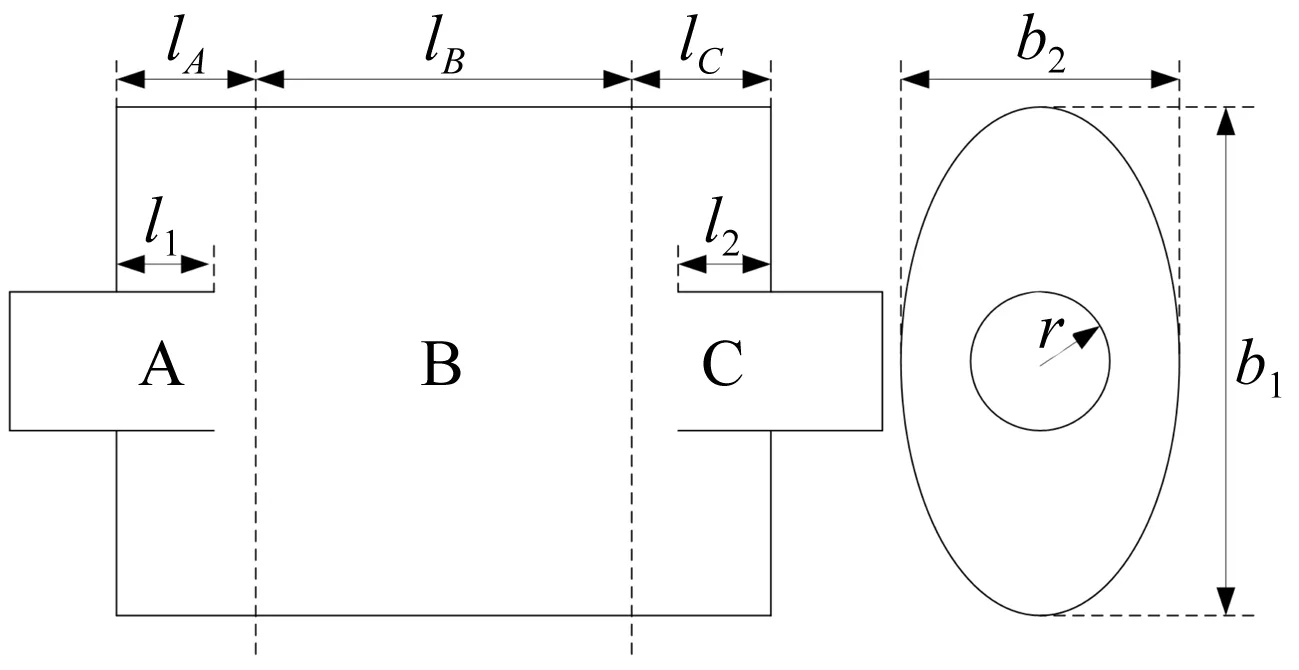
图8　椭圆膨胀腔消声器结构尺寸Fig.8 Structure dimension of elliptical expansion chamber silencer

图9　椭圆截面子区域划分Fig.9 Cross-section division of elliptical interface

图10　椭圆膨胀腔消声器传递损失Fig.10 TL of elliptical expansion chamber silencer

简化混合方法与传统子结构边界元方法在频率1 000 Hz时计算时间比较见表2。以方形穿孔管阻性消声器与椭圆膨胀腔消声器为例，所有计算均在Intel i7 3632QM, 2.2GHz计算机上进行。由于用简化混合方法计算B的阻抗矩阵，整个子结构无需划分网格，只选适当的配点，每次计算求解的矩阵规模远小于传统边界元方法，子结构B的阻抗矩阵计算时间基本可忽略不计，因此简化混合方法能节省大量机时。实际应用中，对尺寸较大消声器，划分子结构进行传递损失计算时，混合方法优势较明显。

表2　消声器传递损失计算时间比较

5结论

(1) 对含若干等截面、非等截面子结构消声器，可分别考虑用配点法、边界元方法计算各自阻抗矩阵，并将其连接进行传递损失计算。

(2) 压缩阻抗矩阵可节省机时。简化混合方法在保证计算精度同时能有效减少计算时间，尤其适用具有较长等截面子结构大尺度声学问题计算。

参 考 文 献

[1] Selamet A, Ji Z L. Acoustic attenuation performance of circular expansion chambers with offset inlet/outlet: I.analytical approach[J]. Journal of Sound and Vibration, 1998, 213(4): 601-617.

[2] Selamet A, Ji Z L. Acoustic attenuation performance of circular expansion chambers with extended inlet/outlet[J]. Journal of Sound and Vibration, 1999, 223(2): 197-212.

[3] Selamet A, Ji Z L. Acoustic attenuation performance of circular flow-reversing chambers[J]. Journal of the Acoustical Society of America, 1998, 104(5): 2867-2877.

[4] Selamet A, Xu M B, Lee I J, et al. Analytical approach for sound attenuation in perforated dissipative silencers with inlet/outlet extensions[J]. Journal of the Acoustical Society of America, 2005, 117(4): 2078-2089.

[ 5] Peat K S, Rathi K L. A finite element analysis of the convected acoustic wave motion in dissipative silencers[J]. Journal of Sound and Vibration, 1995, 184(3): 529-545.

[6] Ji Z L. Boundary element acoustic analysis of hybrid expansion chamber silencers with perforated facing[J]. Engineering Analysis with Boundary Elements, 2010,34(7): 690-696.

[7] Wu T W, Cheng C Y R, Zhang P. A direct mixed-body boundary element method for packed silencers[J]. Journal ofthe Acoustical Society of America, 2002, 111(6): 2566-2572.

[8] Lou G, Wu T W, Cheng C Y R. Boundary element analysis of packed silencers with a substructuring technique[J]. Engineering Analysis with Boundary Elements, 2003,27(7): 643-653.

[9] Kirby R, Lawrie J B. A point collocation approach to modelling large dissipative silencers[J]. Journal of Sound and Vibration, 2005, 286(1): 313-339.

[10] Kirby R, Williams P T, Hill J. A three dimensional investigation into the acoustic performance of dissipative splitter silencers[J]. The Journal of the Acoustical Society of America, 2014, 135(5): 2727-2737.

[11] Kirby R, Amott K, Williams P T, et al. On the acoustic performance of rectangular splitter silencers in the presence of mean flow[J]. Journal of Sound and Vibration, 2014, 333(24):6295-6311.

[12] Kirby R. A comparison between analytic and numerical methods for modelling automotive dissipative silencers with mean flow[J]. Journal of Sound and Vibration, 2009, 325(3):565-582.

[13] Fang Z, Ji Z L. Acoustic attenuation analysis of expansion chambers with extended inlet/outlet[J]. Noise Control Engineering Journal, 2013, 61(2):240-249.

[14] Fang Z, Ji Z L. Numerical mode matching approach for acoustic attenuation predictions of double-chamber perforated tube dissipative silencers with mean flow[J]. Journal of Computational Acoustics, 2014, 22(2):1450004-1-1450004-15.

[15] Kirkup S M. Fortran codes for computing the discrete Helmholtz integral operators[J]. Advances in Computational Mathematics, 1998, 9(3/4): 391-409.

[16] Krishnasamy G, Schmerr L W, Rudolphi T J, et al. Hypersingular boundary integral equations: some applications in acoustic and elastic wave scattering[J]. Journal of Applied Mechanics, 1990, 57(2): 404-414.

[17] 方智,季振林. 穿孔管阻性消声器横向模态和声学特性计算与分析[J]. 振动与冲击, 2014, 33 (7):138-146.

FANG Zhi, JI Zhen-lin. Transversal modes and acoustic attenuation performance of a perforated tube dissipative silencer[J]. Journal of Vibration and Shock, 2014, 33(7): 138-146.

[18] 方智,季振林. 穿孔管消声器横截面模态及消声特性的有限元分析[J]. 振动与冲击, 2012, 31(17): 190-194.

FANG Zhi, JI Zhen-lin. Finite element analysis of cross-section modes and acoustic attenuation characteristics of a perforated tube silencer[J]. Journal of Vibration and Shock, 2012, 31(17):190-194.

基金项目：国家自然科学基金(11174065)

收稿日期：2014-11-12修改稿收到日期：2015-01-20

通信作者季振林 男，教授，博士生导师，1965年生

中图分类号:TB535

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.02.025

Transmission loss prediction for silencers by using the combination of boundary element method and numerical collocation approach

YANG Liang1, JI Zhen-lin1, WU T W2

(1. School of Power and Energy, Harbin Engineering University, Harbin 150001, China; 2. College of Mechanical Engineering, University of Kentucky, Lexington 40506, Lexington)

Abstract:A technique combining the boundary element method (BEM) and numerical collocation approach was proposed to calculate the transmission loss of silencers with arbitrary cross-section. The silencer was divided into several substructures. The BEM and the numerical collocation approach were employed combinedly to evaluate the impedance matrices of substructures with non-regular cross-section and axially uniform cross-section respectively, and then the impedance matrices for all substructures were achieved. The transmission loss predictions of several silencers agree well with the results by BEM. The computational efficiency was analyzed and compared with that of the traditional substructure method, the combined technique may save computational time efficiently.

Key words:silencer; transmission loss; boundary element method; numerical collocation approach

第一作者 杨亮 男，博士生，1989年9月生