高温下地聚合物混凝土损伤演化及动态本构模型研究

王志坤， 许金余,2， 任韦波， 白二雷, 董宗戈

(1.空军工程大学 机场建筑工程系，西安　710038；2.西北工业大学 力学与土木建筑学院，西安　710072; 3.空军装备部，北京　100843)



高温下地聚合物混凝土损伤演化及动态本构模型研究

王志坤1， 许金余1,2， 任韦波1， 白二雷1, 董宗戈3

(1.空军工程大学 机场建筑工程系，西安710038；2.西北工业大学 力学与土木建筑学院，西安710072; 3.空军装备部，北京100843)

摘要：采用高温SHPB(Split Hopkinson Pressure Bar )试验系统对高温下地质聚合物混凝土(Geopolymeric Concrete, GC)损伤演化规律及本构模型进行试验研究。结果表明，高温下GC主要力学性能指标呈显著的应变率强化效应及温度弱化效应；利用波阻抗衡量GC的高温损伤可行、有效，所得损伤演化规律能较好表征GC损伤实际情况；以静力本构模型为基础，通过引入应变率强化因子及温度弱化因子构建GC动态损伤本构模型，通过试验结果标定参数，可获得较准确的地质聚合物混凝土动态损伤本构模型。

关键词：地质聚合物混凝土；高温；应变率；损伤；本构模型

地质聚合物[1-2]指碱性环境下由天然矿物或固体废弃物经聚合反应形成的具有非晶态至准晶态特征的致密高强体。地质聚合物混凝土(Geopolymeric Concrete，GC)作为新型建筑材料，较传统硅酸盐混凝土具有更优异的物理化学性能，广泛用于建筑结构。随城市建筑密度增加，火灾、爆炸等灾害事件频发，建筑结构可能遭受高温-冲击耦合荷载侵袭，由于温度梯度及各组分热膨胀系数不匹配等，混凝土类材料在高温下会出现性能劣化，从而危及结构整体性能。因此探究混凝土类材料在高温下的损伤演化规律及本构模型具有较大实用意义。

Simo等[3-4]用内状态变量理论及不可逆热动力学获得高温下混凝土连续弹塑性-损伤本构模型；Ulm等[5]基于屈服准则[6]提出热-化学-塑形本构模型。陈江瑛等[7]基于金属热激活理论，通过对ZWT本构模型适当修改，获得高应变率下水泥砂浆的本构模型。而对高温下GC动态损伤本构模型研究鲜有报道，本文以粉煤灰、矿渣为原料，液体硅酸钠、固体氢氧化钠混合液为激发剂，制备获得地质聚合物混凝土，用自主研制的高温SHPB试验系统[8]对该混凝土进行试验，并利用试件波阻抗变化衡量材料内部高温损伤演化，建立其动态损伤本构方程。

1试验

1.1原材料及试件制备

原材料有：① 粉煤灰，密度2.05 g/cm3，比表面积≥355 m2/kg；② 水淬高炉矿渣，比表面积491.6 m2/kg，28 d活性指数95%；③ 灞河中砂，细度模数2.78，级配合格；④ 石灰岩碎石，粒径5～20 mm，密度2.70 g/cm3；⑤ 片状氢氧化钠固体，纯度97%；⑥ 液体硅酸钠，模数3.1～3.4。表1为地质聚合物混凝土配合比。用电液伺服材料试验系统测得常温标准立方体试件静压强度为56.4 MPa。

表1　地质聚合物混凝土配合比(kg/m3)

试件制备：试件在长圆柱体钢模中浇筑成型，24 h后拆模并标准养护(温度20±2 ℃，相对湿度RH>95%)，28 d后对试件进行切割、打磨抛光以保证其两端面平行度、平整度及光洁度。本试验所用圆柱体试件几何尺寸为98 mm×50 mm。

1.2高温SHPB试验

该系统包括常规SHPB装置与温控系统两部分。图1为箱式电阻炉及温控系统。图2为管式加热炉。

图1 箱式电阻炉图Fig.1Boxheatingfurnace图2 管式加热炉Fig.2Tubularheatingfurnace

试验设5个温度等级，即室温(25℃)、200℃、400℃、600℃、800℃，每个温度下均含5个不同应变率等级，每种工况取3块试件，取平均值作为试验结果。先以10℃/min升温速率对试件加热，达到试验温度后恒温4 h，加热后将其转移至管式加热炉内，在目标温度下恒温10 min后进行冲击试验。用厚度1 mm、直径分别为30 mm、35 mm、40 mm、45 mm、50 mm的铝片作为波形整形器[9]，将各种尺寸整形器与不同试验冲击速度匹配即可使试件在破坏前有足够时间达到应力均匀状态，以保证SHPB数据有效性。不同温度下GC动态压缩试验结果见表2。

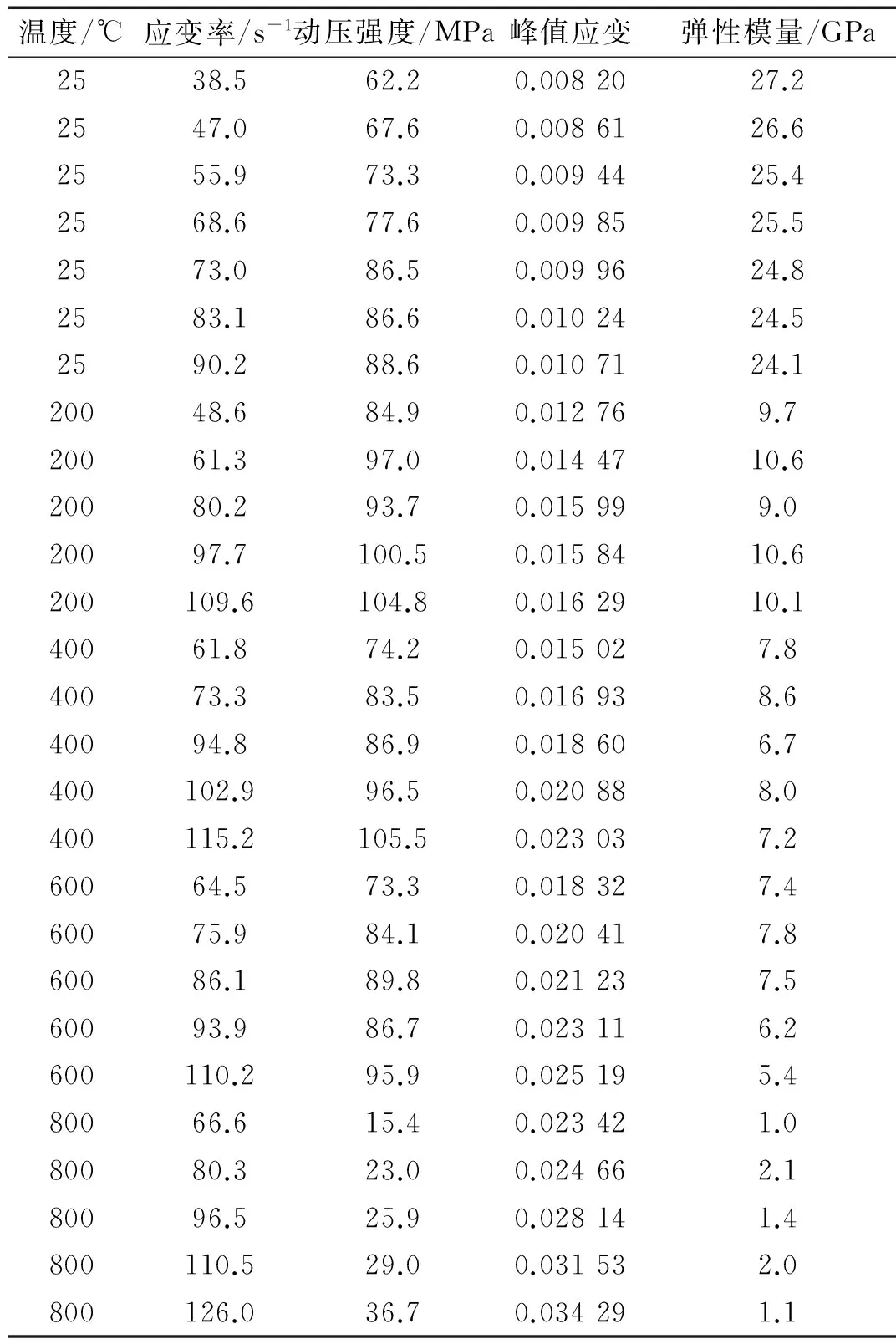
表2　高温下SHPB试验测试结果

2高温下地质聚合物混凝土损伤演化规律

2.1波阻抗计算表达式

高温下受试验技术水平限制，难以获得直接反映材料损伤的参数指标，常规损伤变量定义方式无法应用。金解放等[10]采用以波阻抗定义损伤变量方式研究静荷载与循环冲击荷载组合作用下岩石动态力学特性，本文对该方法进行相应修正，用以研究高温下GC损伤演化规律及本构关系。

图3为SHPB压杆装置中应力波传播示意图，图中ρ0V0为试件波阻抗；ρeVe为压杆波阻抗；L为试件长度；σI，σR，σT分别为入射、反射及透射波。

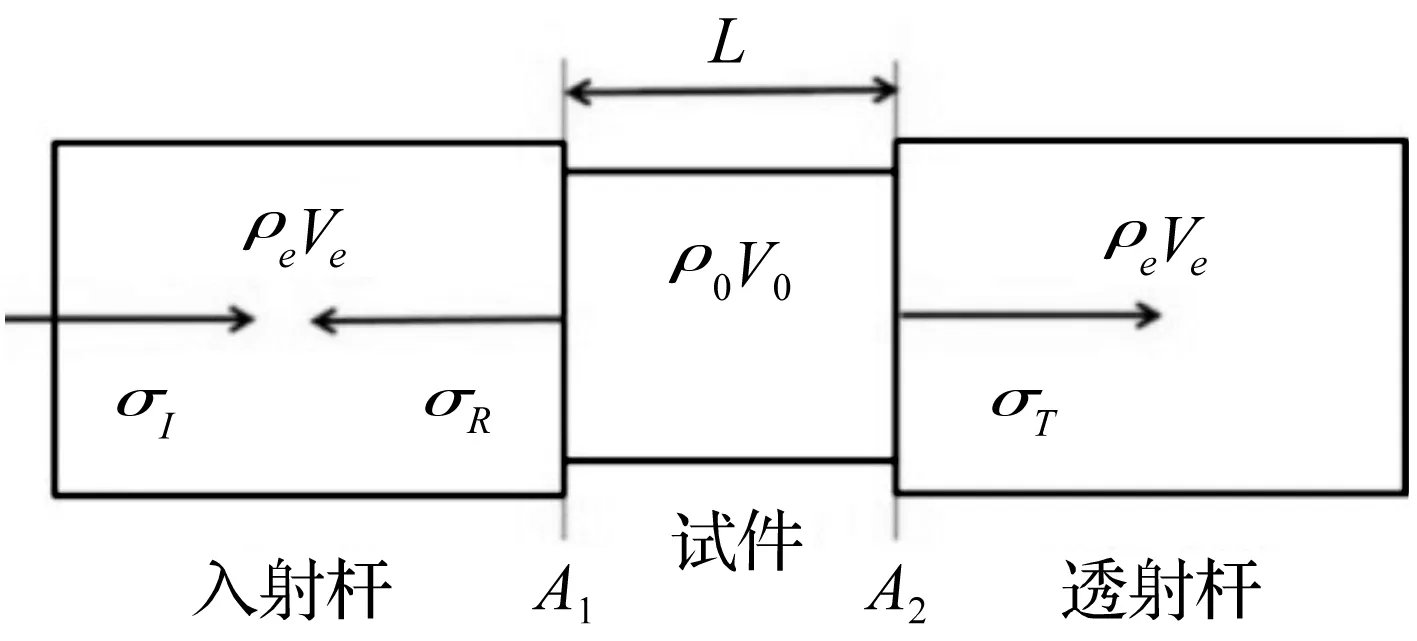
图3　SHPB装置中应力波传播示意图Fig.3 Propagation graph of stress wave on SHPB

应力波由入射杆经试件传入透射杆过程中会在A1、A2界面发生多次透反射，A1界面有一次及高次反射波σRi(t)，A2界面有一次及高次透射波σTi(t)。本文仅考虑应力波在A1界面第一次透反射形成的σR1(t)及A2界面第二次透反射形成σT1(t)，并令σR1(t)=σR(t)，σT1(t)=σT(t)。

据一维弹性波理论，应力波传播中在A1、A2界面须满足：两侧介质内力须相等及质点速度须连续。由此可得

σR(t)=ξσI(t)

(1)

(2)

(3)

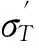
σT(t)=(1-ξ)(1+ξ)σI(t)

(4)

由式(1)、(4)可知，若已知应力波σI(t)，σR(t)，σT(t)及ρeVe即可反解出试件波阻抗ρ0V0，表达式为

(5)

ρ0V0=

(6)

(1)σR(t)与σT(t)分别为入射波σI(t)在A1界面的一次反射波与A2界面的一次透射波，而SHPB系统中应变片所得应力波为在界面上经多次透反射形成的叠加波形，因此，须摒弃测量结果中高次透反射波。据推导知，A1界面的二次反射波为

(7)

(2) 式(5)、(6)均可求解试件波阻抗，可分别侧重反、透射波的应用，探寻两种求解方式区别，以获得最优求解方法。SHPB试验中，反、入射波信号由同一应变片记录，可能受干扰有误差，而透射波信息精确性较高，故用式(6)进行试件波阻抗计算。

图4为利用入、透射波所得波阻抗-时间曲线。由图4看出，随时间推移试件波阻抗呈先增大后减小趋势，且存在一较明显的平台段。加载前期试件逐渐被挤压密实，随密实度提高其波阻抗自然呈现增长趋势；下降段则主要体现冲击荷载对试件的损伤作用，继续加载，试件破坏程度加剧，缺陷数量增加，波阻抗值减小。计算中取平台段均值作为试件最终波阻抗值，此阶段波阻抗数值已趋于稳定且能充分体现高温对试件造成的损伤。

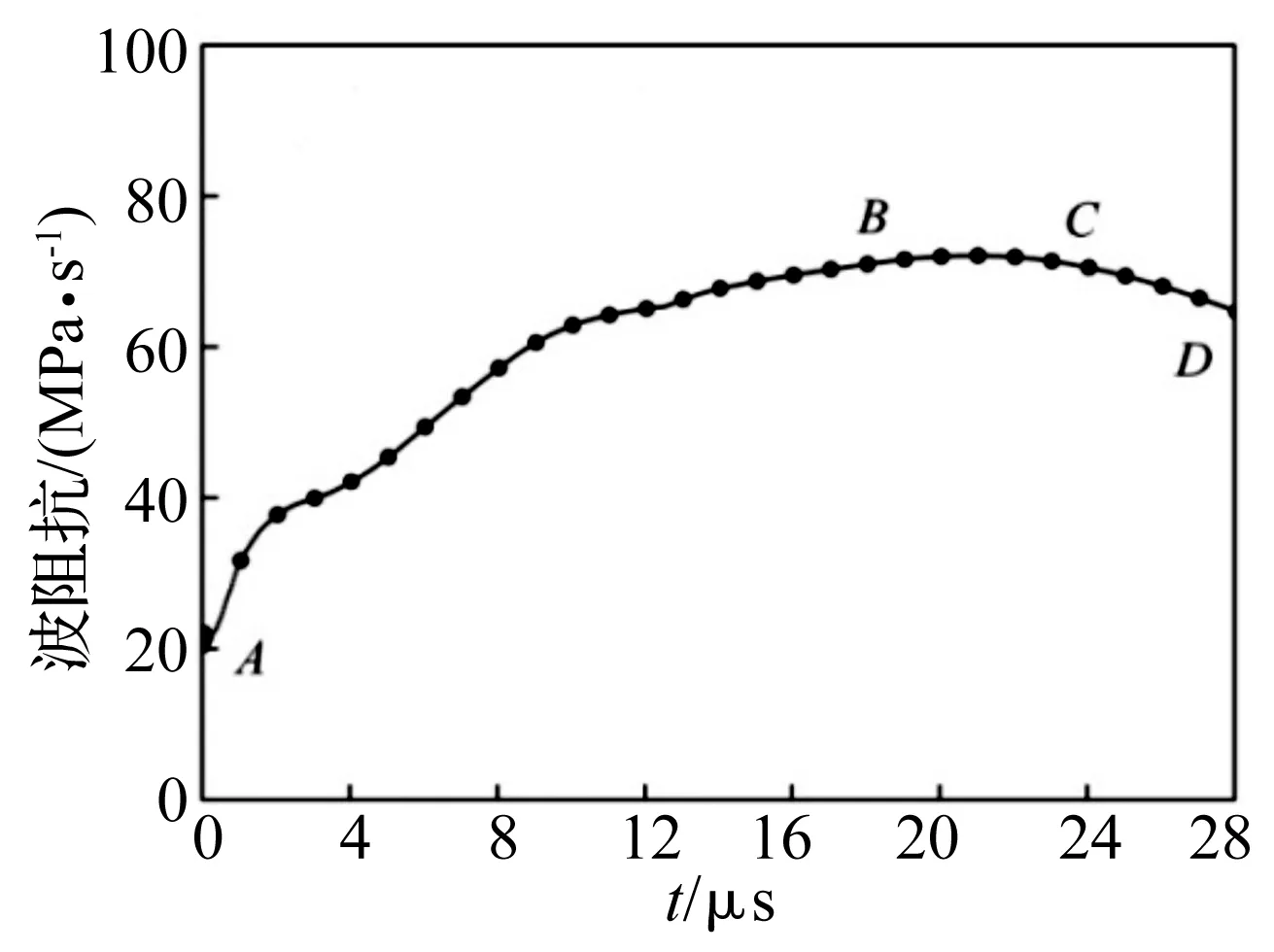
图4　实测数据计算的波阻抗变化趋势Fig.4 Variation curve of wave impedance calculated by testing data

2.2试验验证

参考几种常规损伤变量定义方式，确定本文损伤变量形式为

(8)

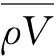
对试件进行超声波检测，得加热前其平均初始波速为4 310.4 m/s。已知试件厚度50 mm，则其波阻抗计算时间区段为0～26.4 μs。图5为据式(6)计算的波阻抗随加载时间变化趋势(篇幅所限，仅给出部分典型工况图像)。由图5可见，试件波阻抗随温度升高显著降低，温度弱化效应明显；同一温度、不同应变率(较低、较高水平)对试件波阻抗值影响不大，仅一定程度上改变波阻抗曲线形态，较低应变率下波阻抗峰值及平台段出现晚，从侧面反映出本文所用波阻抗计算方法能在相当程度上摒弃冲击对试件波阻抗的影响。

对同一温度水平、5个应变率等级的波阻抗取均值，可得试件经温度损伤(常温下为初始损伤)的波阻抗，高温损伤前波阻抗值可由称重及声学检测等计算得出。图6为试件波阻抗随温度变化，图7为损伤变量D与温度的关系。由图7看出，随温度不断升高试件波阻抗持续减小，损伤程度逐渐增加，温度越高损伤越剧烈，800 ℃时试件D值高达0.715；200 ℃～400 ℃时GC呈较好的耐热性，损伤程度不大；温度达400 ℃～800 ℃时试件损伤增长明显，性能急剧劣化；其中400 ℃～600 ℃损伤增长最显著，而600℃～ 800 ℃时增长趋势相对平缓。经回归分析所得高温下GC试件损伤度与温度关系为

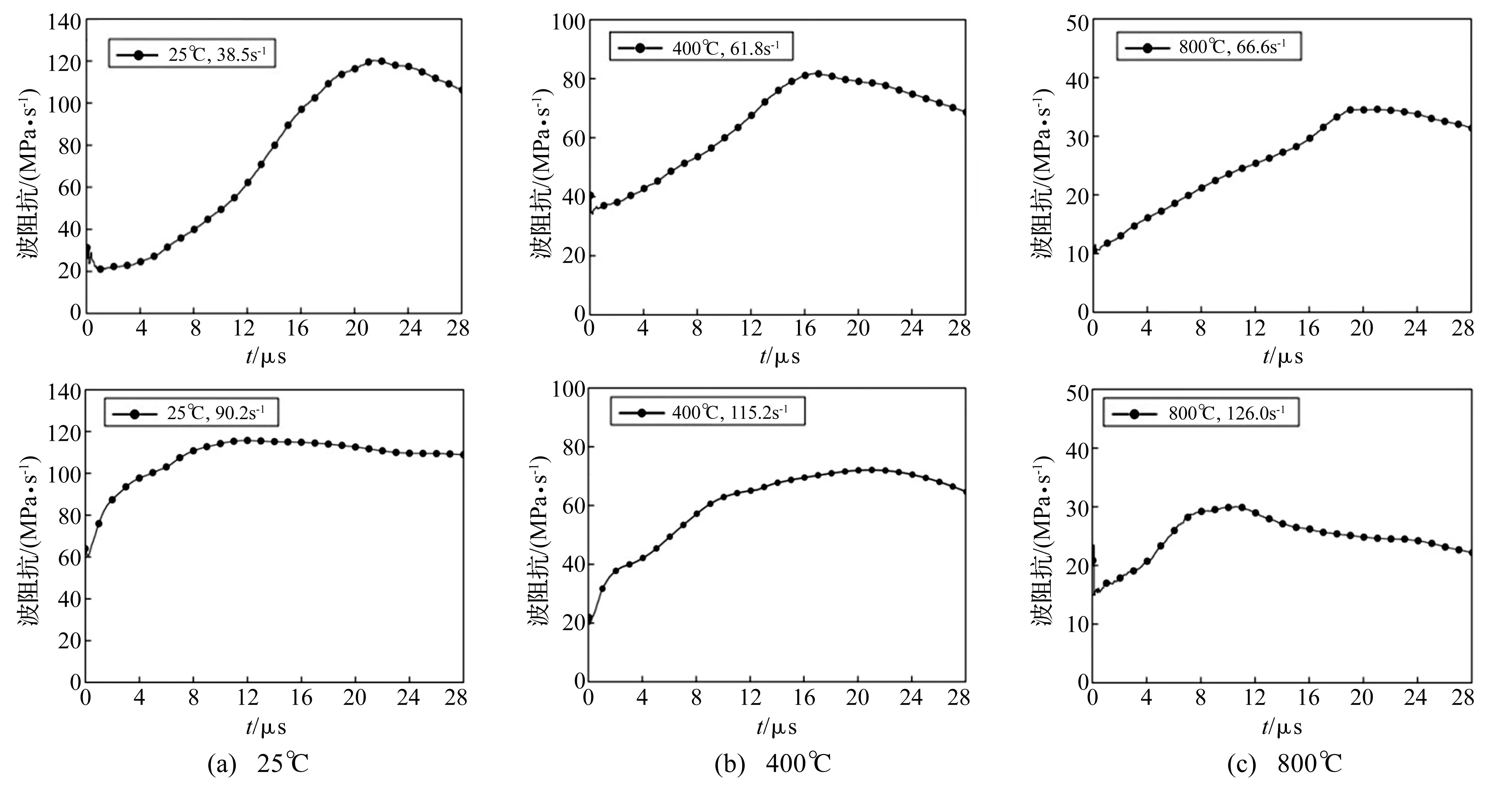
图5　不同温度的波阻抗-时间曲线Fig.5 Wave impedance-time curve at different temperatures

(9)

关于GC损伤演化曲线变化趋势可解释为：200 ℃～400 ℃时，在温度及水蒸汽作用下材料内部的硅铝酸盐物质发生络合、聚合反应，新生反应产物一定程度上弥补之前的温度损伤，因而损伤增长并不明显。400 ℃～600 ℃时试件内部水蒸汽蒸发殆尽，二次聚合反应不再进行，试件损伤作用逐渐显著，加之各相间热差异性凸显，宏观表现为试件损伤增长极迅速。600 ℃～800 ℃时试件内部虽会进一步产生高温损伤，但600 ℃前已积累相当程度的高温损伤，损伤增长空间有限，表现为损伤演化曲线增长趋势相对平缓。

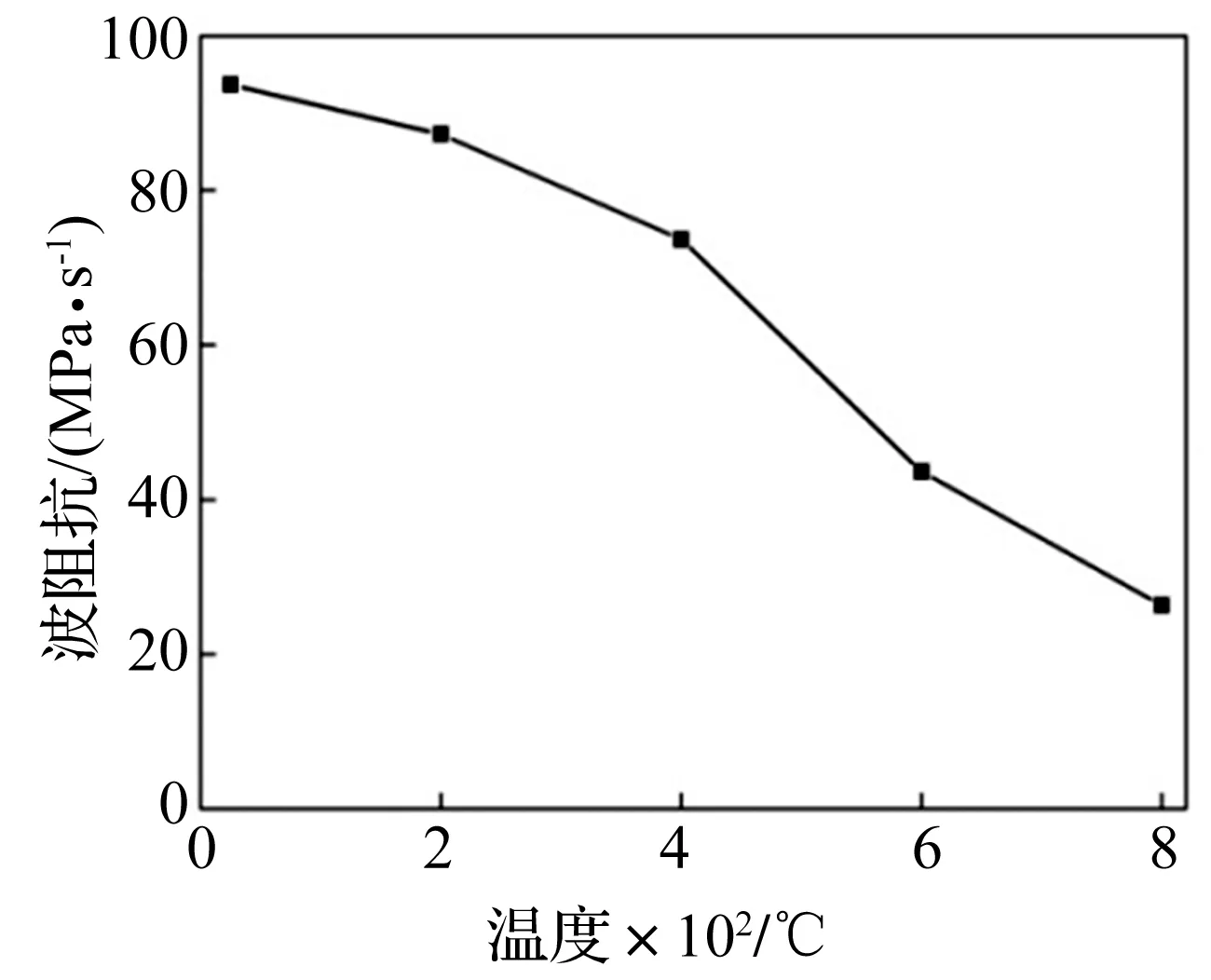
图6　波阻抗与温度关系Fig.6 The relationship between wave impedance and temperature

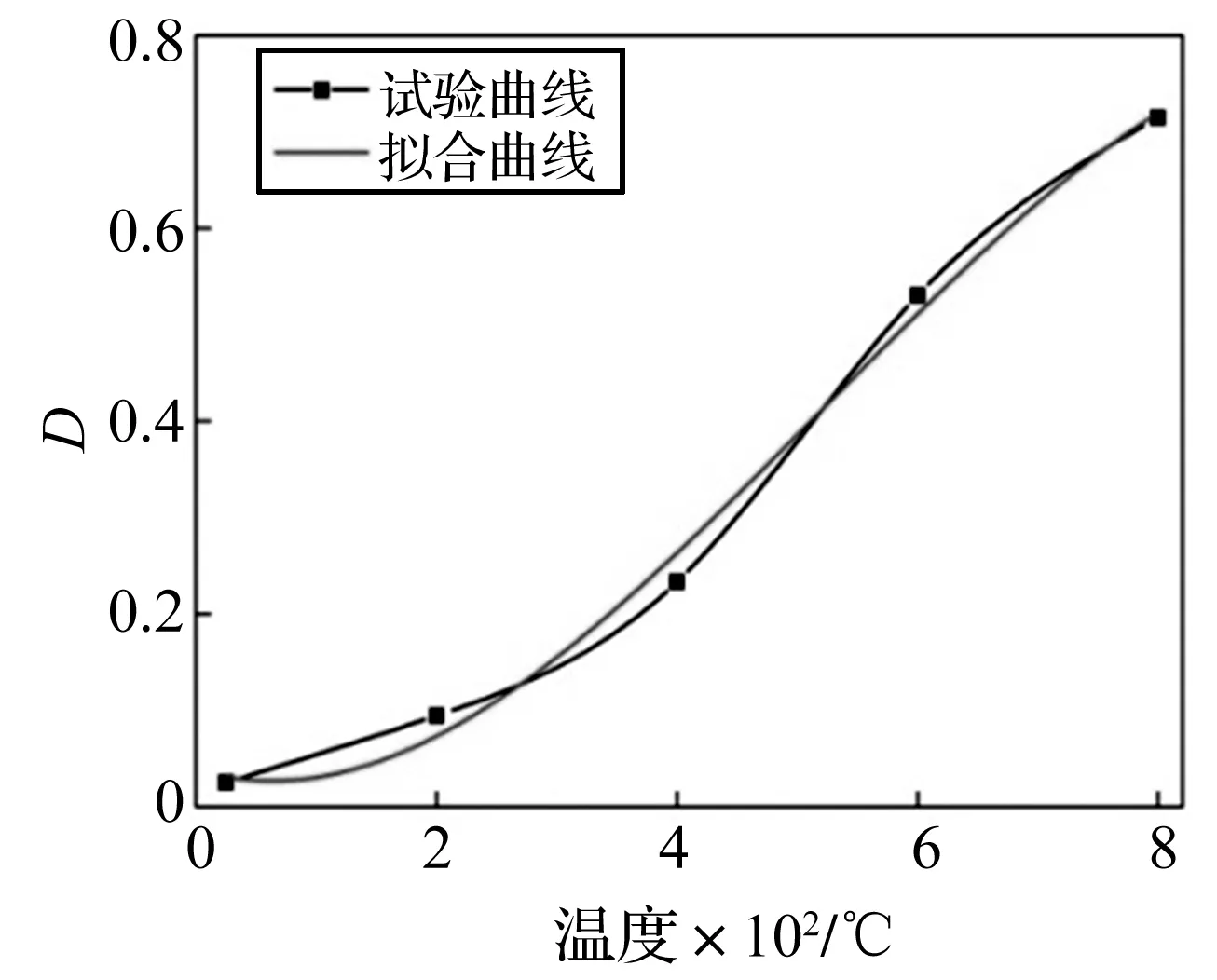
图7　损伤变量D与温度关系Fig.7 The relationship between damage variable and temperature

3本构模型构建

以静态本构模型为基础，通过模型修正计入温度、应变率等因素影响，在试验数据基础上构建高温下GC经验型动态本构模型。静态本构模型用非线性弹性本构模型[11]，该模型形式简单，待定参数较少，物理意义明确且易通过试验数据回归确定，具体形式为

(10)

式中：fcs为混凝土常温下单轴静压强度；εo为静态压缩峰值应变；σs，εs分别为试件应力与应变(以受压为正)；M，n为曲线形状控制参数。

对试验的高温动载工况分别引入应变率强化因子Rrate及温度弱化因子KT=1-D对静压强度fcs进行修正，即

fd=fcsKTRrate

(11)

式中：fd为试件实际动压强度。

由H-J-C模型[12]采用应变率强化因子经验式，将应变率强化因子Rrate定义为以应变率对数为自变量的函数，即

(12)

对材料高温下动态峰值应变特性，拟合获得每一温度下应变率与峰值应变关系，将应变率与温度产生的影响内化于拟合关系式中，达到对材料变形特征的修正，即

(13)

式中：B1～B4为模型参数；其余同上。

(14)

式中：K1～K8为模型参数；其余同上。

通过修正，最终得高温下地质聚合物混凝土动态损伤本构模型方程为

(15)

式(15)中具体拟合参数见表3、表4。模拟、试验曲线对比见图8(篇幅所限，仅选部分典型工况)，高温下地质聚合物混凝土破坏形态见图9。由图8看出，高温下各条曲线峰后应变达最大值后出现回弹，原因主要为：在较低应变率下试件破坏形式基本为留核破坏(见图9)，破坏后仍能保持一定整体性，其核心区域在受力过程中近似弹性状态，因此卸载后出现应变回弹现象；管式加热炉壁会限制试件破坏的横向变形与扩张，影响其峰后变形，亦会导致试件应力应变曲线出现回弹。除此之外，800 ℃时试件应力应变曲线上升段存在一定波动，因其内部已发生严重高温损伤，裂隙、缺陷大量萌生，使加载初期应力应变关系不稳定，且800 ℃时热冲击会对应变片采集信号产生一定影响，宏观表现为加载初期应力应变关系失稳。

表3　强度及变形参数

表4　形状参数

总体看，模拟曲线与试验曲线吻合程度较高，能较准确描述材料的应力应变关系，但在曲线下降段精度较差，因管式炉特殊构造一定程度上影响试件峰后变形；受荷过程中试件到达峰值应力后迅速失稳破坏，呈显著的应力不均匀性，此时力学响应已不完全取决于材料本身属性，而受试件尺寸、结构及破坏过程等因素影响，造成曲线下降段变化较离散。因此，误差在可接受范围内，即所建模型整体上可较准确反映不同温度作用下GC的动态力学特性。

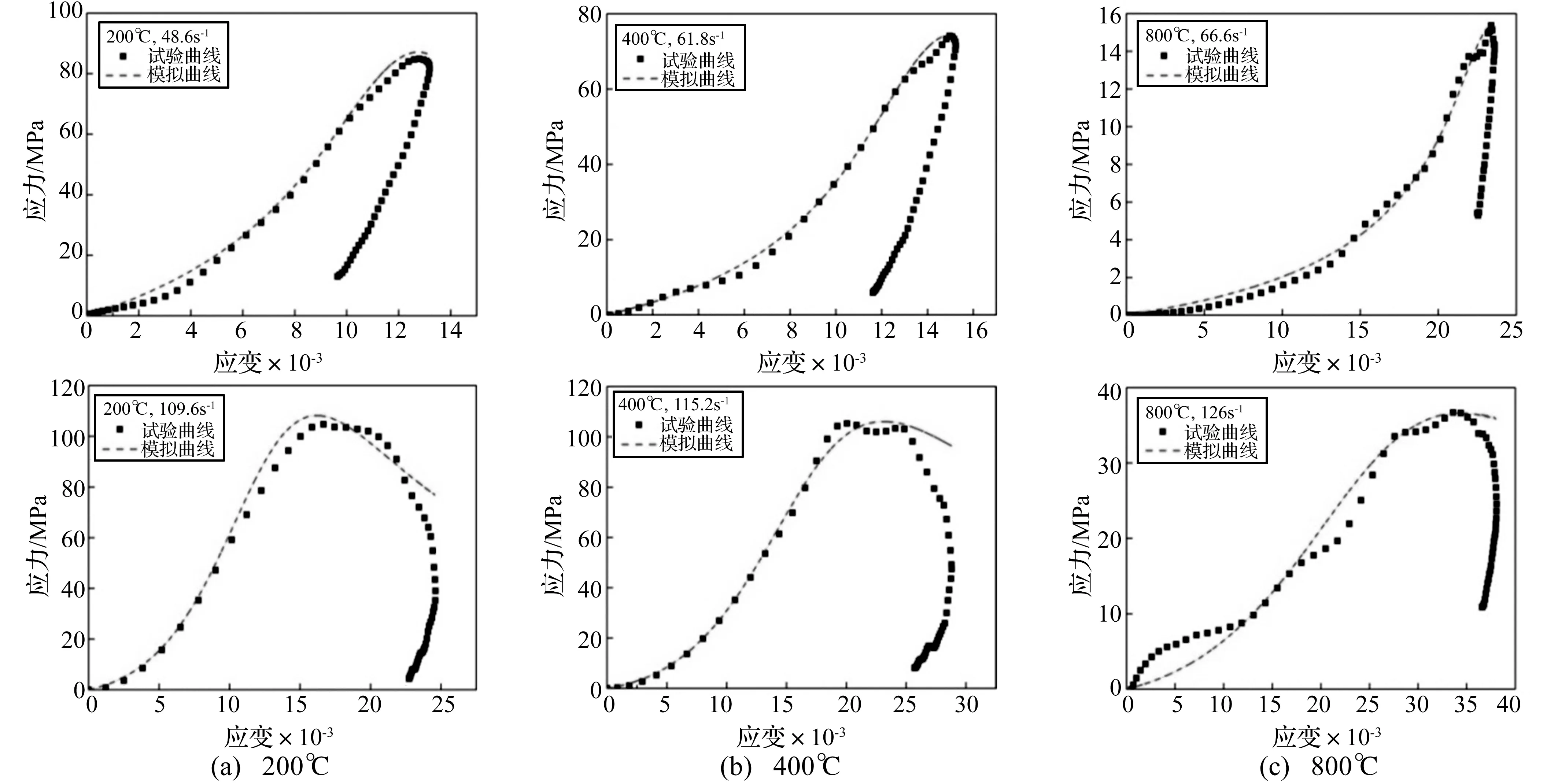
图8　模拟、试验曲线对比Fig.8 The comparison between the simulating curve and the test curve

图9　高温下地质聚合物混凝土破坏形态Fig.9 Damage forms of geopolymeric concrete at elevated temperatures

4结论

(1) 高温下GC主要力学性能指标均呈显著的应变率强化效应及温度弱化效应，温度越高劣化程度越严重。

(2) 利用波阻抗定义GC的高温损伤可行、有效，随温度损伤演化规律能较好表征GC高温损伤的实际情况。

(3) 以混凝土静力本构模型为基础，引入应变率强化因子及温度弱化因子可建立GC高温下动态损伤本构模型，各参数均可通过试验标定，模拟结果与试验结果吻合程度高，能较准确描述高温下地质聚合物混凝土动力学特性。

参 考 文 献

[1] 许金余,罗鑫,吴菲,等. 地质聚合物混凝土动态劈裂拉伸破坏的吸能特性[J]. 空军工程大学学报:自然科学版, 2013,14(5): 85-88.

XU Jin-yu,LUO Xin, WU Fei, et al, Energy absorption capacities of geopolymer concrete under condition of dynamic splitting-tensile damage[J]. Journal of Air Force Engineering University:natural science edition, 2013, 14(5): 85-88.

[2] Davidovits J. Geopolymers and geopolymeric materials[J]. Journal of Thermal Analysis and Calorimetry, 1989, 35(2):429-441.

[3] Simo J C, Ju J W. Strain-and stress-based continuum damage models I. formulation[J]. International Journal of Solids and Structures, 1987, 23(7):821-840.

[4] Simo J C, Ju J W. Strain-and stress-based continuum damage models II. computational aspects[J]. International Journal of Solids and Structures, 1987, 23(7):841-869.

[5] Ulm F J, Coussy O, Bazant Z P. The “chunnel” fire. I: chemoplastic softening in rapidly heated concrete[J]. Journal of Engineering Mechanics, ASCE, 1999, 125(3):272-282.[ 6] Willam K J, Warnke E P. Constitutive model for the triaxialbehaviour of concrete[C]//IABSE Proc. 19, Seminar on Concrete Structure Subjected to Triaxial Stresses,Zurich: International Association for Bridge and Structural Engineering, 1975.

[7] 陈江瑛,王礼立.水泥砂浆的率型本构方程[J].宁波大学学报:理工版, 2000,13(2):1-5.

CHEN Jiang-ying, WANG Li-li. Rate-dependent constitutive equation of cement mortar[J]. Journal of Ningbo University: Natural Science & Engineering Edition,2000,13(2):1-5.

[8] 许金余,刘健,范飞林,等. 高温SHPB冲击实验技术及其应用[J]. 高压物理学报, 2013, 27(1):57-62.

XU Jin-yu, LIU Jian, FAN Fei-lin, et al. A high temperature SHPB impact experimental technique and its application[J]. Journal of High Pressure Physics, 2013,27(1):57-62.

[9] 许金余,赵德辉,范飞林.纤维混凝土的动力特性[M].西安:西北工业大学出版社, 2013.

[10] 金解放,李夕兵,殷志强,等.循环冲击下波阻抗定义岩石损伤变量的研究[J].岩土力学,2011,32(5): 1385-1393.JIN Jie-fang, LI Xi-bing, YIN Zhi-qiang, et al.A method for defining rock damage variable by wave impedance under cyclic impact loadings[J].Rock and Soil Mechanics, 2011,32(5): 1385-1393.

[11] Tsai W T. Uniaxial compressional stress-strain relation of concrete[J]. StructEng,1988, 114(9): 2133-2136.

[12] Holmquist T J, Johnson G R, Cook W H. A coputational constitutive model for concrete subjiected tolarge strains high strain rates and high pressures[C]//Fishler E, ed. 14thInternational Symposium on Ballistics, Canada,IEEE Press, 1993:591-600.

基金项目：国家自然科学基金项目(51378497)；陕西省青年科技新星项目(2013KJXX-81)

收稿日期：2014-06-30修改稿收到日期：2014-12-05

通信作者许金余 男，博士，教授，博士生导师，1963年生

中图分类号:TU528.572

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.02.018

Damage evolution and dynamic constitutive model of geopolymeric concrete at elevated temperature

WANG Zhi-kun1, XU Jin-yu1,2, REN Wei-bo1, BAI Er-lei1, DONG Zong-ge3

(1. Department of Airfield and Building Engineering, Air Force Engineering University, Xi’an 710038, China;2. College of Mechanics and Civil Architecture, Northwest Polytechnic University, Xi’an 710072, China;3. The Air Force Equipment Department, Beijing 100843, China)

Abstract:The damage evolution and dynamic constitutive model of geopolymeric concrete at elevated temperature were investigated using a high temperature SHPB (Split Hopkinson Pressure Bar) test system. The results show that the major mechanical performance indexes reveal the prominent effects of temperature and strain rate. The wave impedance can be used to measure the thermal damage of geopolymeric concrete, and the damage evolution law has a good agreement with the actual situation. Based on the static constitutive model, the dynamic damage constitutive model of geopolymeric concrete considering the effects of temperature and strain rate was established, and the indexes can be determined by experimental results. The model can accurately describe the dynamic characteristics of geopolymeric concrete at elevated temperature.

Key words:geopolymeric concrete; elevated temperature; strain rate; damage; constitutive model

第一作者 王志坤 男，博士生，1990年生