基于SPH-FEM方法的水下近场爆炸数值模拟研究

姜忠涛， 王　雷， 孙鹏楠， 黄　潇

(1.哈尔滨工程大学 船舶工程学院，哈尔滨　150001； 2.哈尔滨船舶锅炉涡轮机研究所，哈尔滨　150001)



基于SPH-FEM方法的水下近场爆炸数值模拟研究

姜忠涛1， 王雷2， 孙鹏楠1， 黄潇1

(1.哈尔滨工程大学 船舶工程学院，哈尔滨150001； 2.哈尔滨船舶锅炉涡轮机研究所，哈尔滨150001)

摘要：针对结构水下近场爆炸载荷作用响应求解难点，通过改进的三维轴对称光滑粒子流体动力学方法(Smoothed Particle Hydrodynamics, SPH)计算获得近场爆炸载荷后传输给非线性有限元软件ABAQUS，利用声固耦合模型对结构响应进行时域非线性计算，形成预报水下近场爆炸载荷对结构毁伤的SPH-FEM模型，实现从药包起爆、结构大幅变形、局部撕裂直至完全剪切破坏的全过程模拟，对载荷时历曲线进行试验验证。计算背空矩形钢板在近场爆炸载荷的响应表明，数值结果与试验值吻合良好。SPH-FEM模型计算效率高、可操作性强，易推广至大型复杂结构受水下近场爆炸毁伤的分析与评估。

关键词：舰船工程；矩形钢板；近场爆炸；SPH-FEM；结构毁伤

水下近场爆炸严重威胁海战的舰船[1]。大当量爆炸会导致舰船局部破坏甚至失去动力，因此对水下近场爆炸研究具有重大意义[2]。

研究近场爆炸作用的结构响应有两个难点，即爆炸载荷强度确定及结构瞬态强非线性响应计算。较水下爆炸试验，理论计算、数值模拟因成本低、效率高、周期短颇受关注[3]。传统方法中对近场爆炸毁伤效果用半经验公式估算，但只对简单板架有效[4]，不适用如水面舰船、潜艇等复杂结构形式。而功能强大的流固耦合分析软件可用于水下近场爆炸结构毁伤预报，如LS-DYNA、AUTODYN等。计算区域较大时两软件计算量极大，效率较低。ABAQUS在工程中应用程度较高，主要因其计算效率高，适用于水面舰船、潜艇等复杂结构[5]。而ABAQUS目前只局限于中远场爆炸计算，原因为传统方法中采用半经验公式确定水中爆炸载荷[6]，而半经验公式只对爆距大于6倍装药半径有效，因此需通过其它有效手段如试验、数值模拟等获取近场爆炸载荷。

考虑工程中水下爆炸装药形式一般为球形或柱形，符合轴对称特点[7]。本文用新的无网格轴对称SPH法[8-9,16-17]计算水中近场爆炸载荷。较纯三维SPH法，轴对称SPH法计算效率极大提高。由于离散区域小，将粒子划分得很密，可提高计算精度。用SPH方法获得爆炸载荷后在ABAQUS中将载荷施加到结构表面进行响应计算，形成适用于近场爆炸计算的SPH-FEM方法。

矩形板作为海洋结构物中最普遍的结构形式，研究其在近场爆炸载荷作用下的响应具有重要意义[10-11]。由于矩形板结构形式简单，试验数据丰富，可为数值验证提供基础。基于SPH-FEM模型，本文计算不同厚度矩形板受近场爆炸载荷响应，并与试验数据进行对比，验证SPH-FEM模型的精度及有效性。数值结果分析表明，矩形板在近场爆炸作用下的失效模式主要为塑性大变形、边缘局部张力撕裂及完全剪切破坏。

1理论模型

1.1三维轴对称SPH方法

传统SPH中场函数f(r)的核近似〈f(r)〉[12-13]为

f(r)≈〈f(r)〉=∫Ωf(r′)W(r-r′,h)dr′

(1)

式中：r为所求点矢量坐标；r′为r紧支域Ω内插值点；W(r-r′,h)为光滑核函数。

本文所用三次样条核函数为

(2)

所求三维问题具有轴对称特性时可将式(1)在柱坐标中表示，先沿周向θ积分，再沿径向r及高度z向积分，即

(3)

式中：

(4)

据式(2)光滑核函数定义0≤R<2时，W有意义，因此可推导θ取值范围为

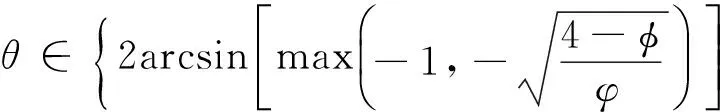
(5)

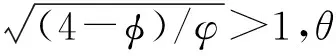
(6)

将式(6)代入式(3)，得柱坐标下核近似积分式为

〈f(r,z)〉=∫SWCf(r′,z′)r′dr′dz′

(7)

由式(7)知，三维积分方程已简化为坐标平面r-z内的二维积分，已极大降低SPH方法计算量，提高效率。由于可在r-z平面内布置较密集粒子，计算精度亦极大提高。因所求问题具有轴对称性，故f(r,z)在θ方向无变化，只需求解f(r,z)在r轴、z轴方向偏导数，即

(8)

核函数的偏导数为

(9)

本文计算程序中，式(9)用数值积分计算。

1.2控制方程

利用式(8)将N-S方程进行离散，即

(10)

式中：ρ，v，e，m为粒子密度、速度、内能及质量；∏ij为人工粘性。

据质量守恒，mjrj=ρjΔrjΔzjrj在整个计算过程中保持不变。此时仍需引入状态方程将连续方程、动量方程及能量方程解耦。水的Mie-Grüneisen状态方程为：

(1)μ>0时水处于压缩状态，有

(γ0+aμ)e

(11)

(2)μ<0时水处于膨胀状态，有

p=ρ0C2μ+(γ0+aμ)e

(12)

式中：ρ0为流体质点初始密度；C为声速；γ0为Grüneisen系数；S1,S2,S3为材料Hugonoit常数；a为体积修正系数。

Mie-Grüneisen状态方程中具体参数见表1。

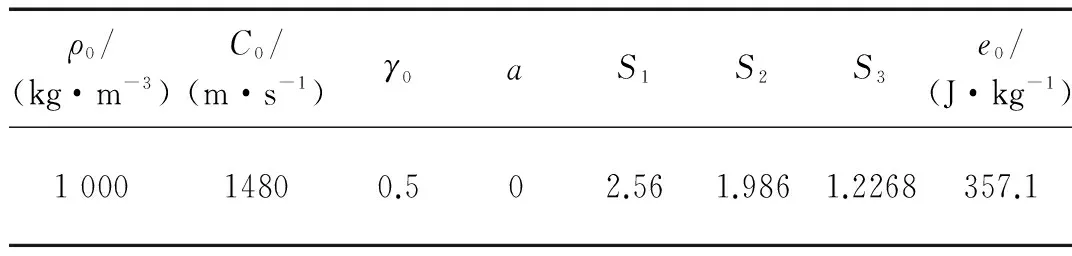
表1　Mie-Grüneisen状态方程中相关参数

TNT爆轰物采用JWL(Jones-Wilkins-Lee)状态方程，即

(13)

式中：ei为单位质量内能；η=ρ/ρ0；A，B，R1，R2，ω为由实验数据拟合的常数，具体见表2，其中E0为初始单位质量内能。

表2　JWL状态方程中相关参数

1.3变光滑长度

模拟TNT爆轰过程中粒子间距逐渐增大，此时需更新光滑长度，否则会出现紧支域内粒子数量不足而产生巨大离散误差。本文采用光滑长度随时间变化公式[14]，即

(14)

式中：d为空间维度。

尽管该轴对称SPH方法用于模拟三维问题，但核近似只在r-z平面内进行，因此d=2，求出dρ/dt后可利用上一时间步h及ρ求出dh/dt，每个时间步对光滑长度进行更新。

1.4显示积分方法和对称轴处理

1.4.1预测校正积分法

本文用预测校正法对离散控制方程进行显示积分计算。令任意场函数f(r)，预测校正积分法为

(15)

式(15)表示在第n个时间步计算场函数f(r)n变化率Df(r)n/Dt，时间前进Δt/2获得f(r)n+1/2，完成预测步计算。在此基础上计算预测步的场函数变化率Df(r)n+1/2/Dt，在f(r)n上前进一整时间步长获得f(r)n+1，完成校正步计算。本文程序中用恒定时间步长，即Δt=0.06h/C。采用OpenMP并行技术在Inter(R) Core(TM) i7-3770 处理器上实现8线程并行计算，具体并行程序设计见文献[15]。

1.4.2对称轴处理

由于对称轴附近粒子数量较少，离散误差较大，粒子穿透对称轴现象难以避免。采用动态边界法在每个时间步关于对称轴镜像分布相应的虚粒子，其参数设置为

(16)

虚粒子参与式(10)的控制方程求解，为防止虚粒子对称轴附近真实粒子密度、加速度计算产生非物理性影响，设其速度、压力为0。为防止个别粒子穿透对称轴导致计算中断，本文提出反弹算法。即在每个时间步判断粒子是否穿透对称轴，将穿透的粒子位置、速度关于对称轴镜像到坐标分量r的正向。

1.5SPH-FEM联合算法

水下爆炸尤其近场爆炸具有瞬态强非线性特点，完成精确实时耦合计算非常困难。文献[2-3,5]成功将ABAQUS声固耦合算法用于结构受中远场水下爆炸载荷响应计算，其中载荷确定用文献[6]的半经验公式。本文SPH-FEM联合算法计算过程见图1。利用已建三维轴对称SPH方法模拟装药爆轰，其过程通过时域内逐步改变装药粒子种类实现；爆轰波传到水汽界面时高压气团进一步膨胀，在水中辐射出冲击波；数值模型中记录结构所在位置的压力载荷时历曲线。压力载荷得出后程序转到ABAQUS，将载荷施加在结构与水域的耦合面，计算结构非线性动态响应。ABAQUS中选散波(scattered wave)公式进行计算，结构响应由入、散射波响应叠加，能充分考虑结构存在对流场中载荷分布影响。ABAQUS中具体操作过程见文献[3]。

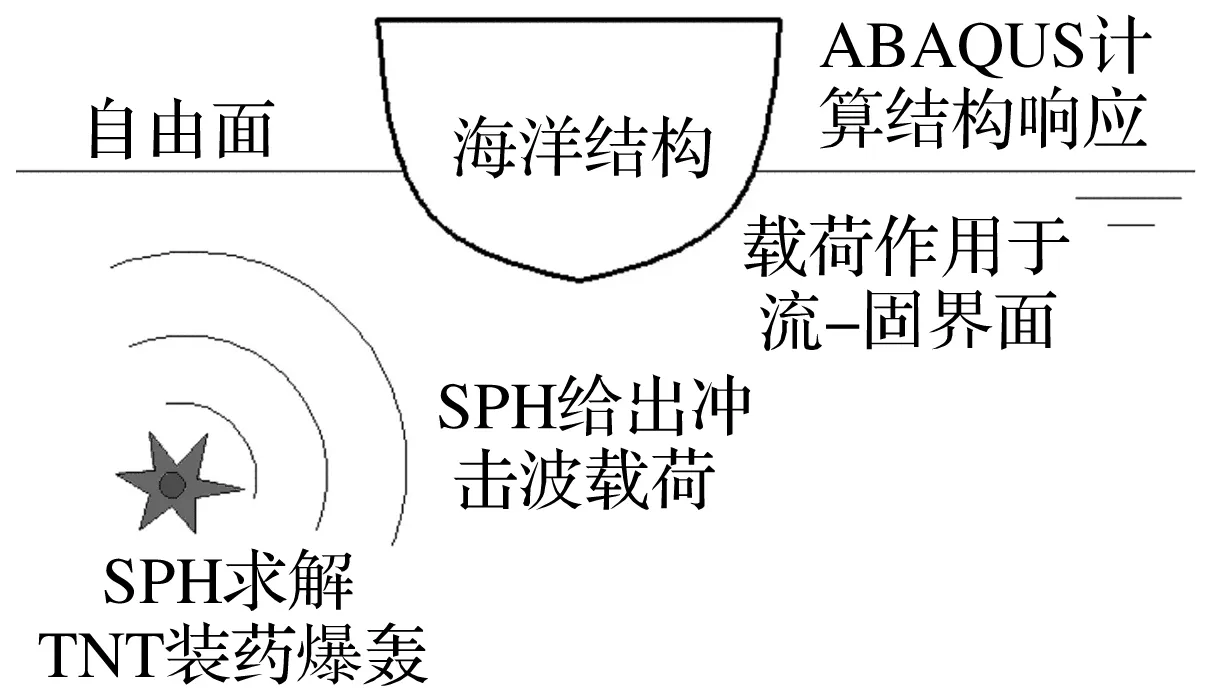
图1　SPH-FEM联合算法求解近场爆炸示意图Fig.1 Sketch of the solving of near-field underwater explosion with SPH-FEM model

结构的弹塑性模型在近场爆炸计算中十分重要，因在此类工况下结构往往产生巨大塑形变形甚至断裂失效。本文采用线性强化弹塑性模型，即

(17)

式中：E为弹性模量；E1为切线模量；σs为屈服应力；εs为应力等于σs时的应变；σf为抗拉强度。

对钢材而言，材料的应变率效应不能忽略。本文采用Cowper-Symonds本构方程计算动态屈服应力，即

(18)

式中：D=40.4 s-1；q=5。

2数值结果与讨论

2.1变光滑长度对精度影响

轴对称SPH模型中对称轴处压力不稳定性问题最难处理。而用变光滑长度技术能较好改善对称轴处气泡膨胀不均匀及冲击波压力不稳定问题。SPH测试模型中初始粒子间距Δx=1.458 mm，球形TNT装药半径r0=29.2 mm，半径方向布置20个粒子，TNT粒子数585。计算水域为球形半径R=291.6 mm，水域粒子数约6.3万个。0.15 kg球形TNT药包在球心起爆0.09 ms时爆炸气泡形状及水域冲击波压力分布见图2。由图2看出，用变光滑长度后球状药包从中心引爆后均匀膨胀，对称轴处冲击波压力分布较均匀，因此模拟装药水下爆炸可压缩问题时，变光滑长度能大幅提高模拟结果精度。

图2　爆炸气泡形状对比Fig.2 The comparison of bubble shapes

2.2自由场水下爆炸载荷验证

为验证本文三维轴对称SPH方法的水中爆炸载荷精度，将轴对称SPH方法模拟自由场水下爆炸冲击波压力时历曲线与试验数据进行对比。试验在中国工程物理研究院进行，工况为8 kg球形TNT药包在自由场爆炸，测量爆距4 m处压力时历曲线。SPH模型中初始粒子间距Δx=5.32 mm，球形TNT装药半径r0=106.4 mm，半径方向布置20个粒子，TNT粒子数618。计算水域为球形，半径R=6.384 mm，水域粒子约227万个。装药在球心起爆，起爆后不同时刻水域冲击波压力云图见图3。由图3看出，TNT爆轰后形成的高压气泡沿各方向均匀膨胀，气泡呈球形，冲击波压力云图在r-z平面内沿各角度分布均匀，对称轴处未见压力不稳定现象。

图3　不同时刻高压气泡膨胀及冲击波压力云图Fig.3 The shock wave pressure contour and the expansion of the high-pressure bubble

爆距4 m处冲击波压力时历曲线见图4。由图4看出，SPH模拟结果与试验结果吻合良好，未出现传统数值算法中压力波峰非物理性振荡现象，由此验证三维轴对称SPH方法的有效性。

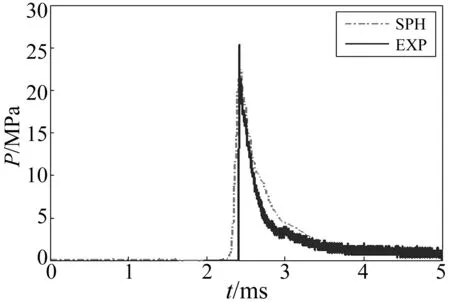
图4　冲击波压力时历曲线试验与SPH结果对比Fig.4 The comparison of the time evolution of the shock pressure between experimental data and numerical results

2.3矩形板近场爆炸验证

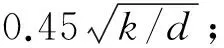
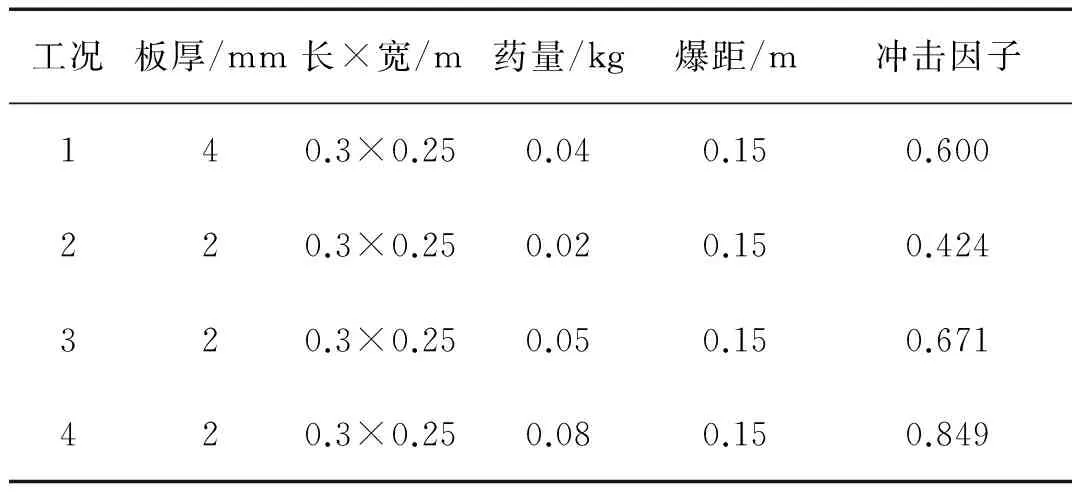
表3　矩形板受近场爆炸试验工况

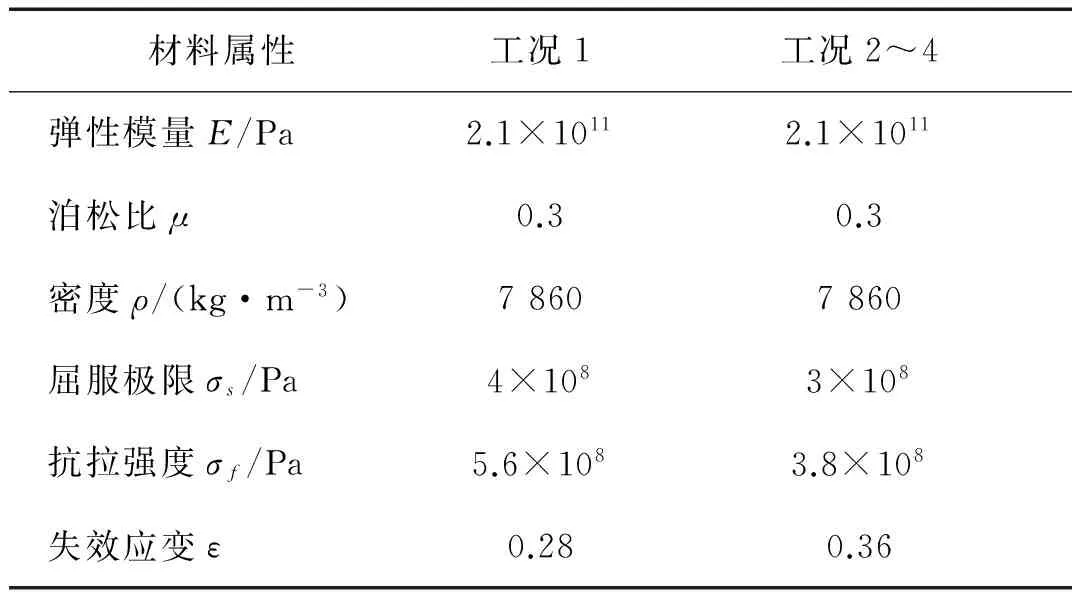
表4　试验所用矩形钢板材料参数

数值模型中用三维轴对称SPH方法计算工况1～4的冲击波载荷。忽略气泡脉动压力及气泡水射流影响。获得冲击波载荷后用ABAQUS建立背空矩形板模型，用四边形网格离散，网格边长5 mm×5 mm，见图5(a)。流场建立半径1 m的半球形水域，利用四面体网格离散。矩形板位于球形水域中心。水域与矩形板重叠部分网格种子间距与矩形板相同；水域外围网格种子间距为0.05 m，见图5(b)。矩形板与水域施加TIE条件，其余表面施加无反射边界条件，矩形板四周施加夹支边界条件。

图5　ABAQUS中建立的背空矩形板近场爆炸模型Fig.5 The numerical model created in ABAQUS

各工况矩形板失效情况见图6。左侧为试验结果，右侧为数值结果。

图6　矩形钢板受近场爆炸载荷作用毁伤情况Fig.6 The damaging of the rectangular plate subjected to near-field underwater explosion

工况1中矩形板厚度4 mm，在40 g装药爆轰作用下发生大幅度永久塑形凹陷。矩形板中心凹陷位移U随时间变化曲线见图7(a)，可见不考虑应变率效应时矩形板凹陷结果较试验值偏大70%，考虑矩形板应变率效应的数值结果与试验值较吻合，稍偏小10%。工况2中矩形板厚度2 mm，在20 g装药爆轰作用下亦发生大幅度塑形永久变形。由图7(b)可知，此时不考虑应变率效应结果仍偏大较多，考虑应变率效应结果偏大5.17%。工况3将装药量提高到50 g，由图6可知，试验中矩形板长边中部出现局部张力撕裂，数值结果较好再现出试验现象。对比图7(c)矩形板中心位移时间曲线知，考虑应变率效应的数值、试验结果误差仅1.87%。由工况1～3数据知，不考虑材料应变率效应时数值结果始终偏大，考虑时相当于增强结构的抗冲击能力，结构响应变小，与试验值更接近，因此应变率效应在本构模型中不可忽略。

工况4中将装药量提高到80 g，此时矩形板发生严重剪切破坏，仅在4个直角处有小块残留破片与夹支边界相连。实验、数值结果中均可发现，脱落钢板形状呈突出状，即钢板在巨大冲击载荷作用下先发生大幅度塑形凹陷后，边缘发生张力局部撕裂，并在张力、剪切力综合作用下发生整体脱落。

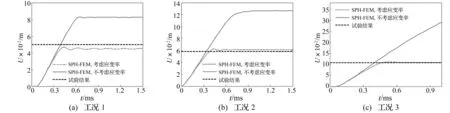
图7　矩形钢板中心凹陷变形随时间变化曲线Fig.7 Time evolution of the bulge deformation on the center of the plate

表5为试验值、计算值误差统计，考虑材料应变率效应的数值结果误差均保持在10%以内，可见本文SPH-FEM方法能较准确预报矩形板在近场爆炸载荷作用下的响应。而对不同工况，计算值在试验值上下浮动，并非全部偏大或偏小，可见考虑应变率效应的本构模型是有效的。

由数值结果显示的钢板变形随时间演化过程分析知，钢板先发生凹陷变形，随后边缘达到屈服极限，边缘张力达到强度极限时出现局部张力撕裂。长边中点最先达到强度极限断裂(图6(c))。随局部撕裂扩展及剪应力共同作用下矩形板完全脱落，即在近场爆炸载荷作用下的失效模式为随冲击因子增加钢板失效程度逐渐递增，依次表现为大幅度永久凹陷，边缘局部张力撕裂及剪切破坏。

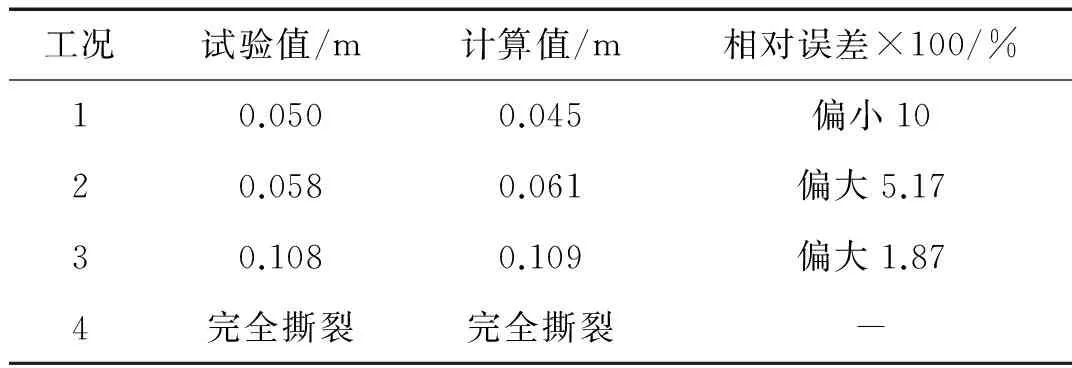
表5　试验值与计算值误差分析

3结论

(1) 通过采用变光滑长度技术，改进对称轴处的数值处理，可有效提高三维轴对称SPH方法预报水下近场爆炸载荷精度，载荷结果与试验值吻合良好。 将载荷曲线施加到ABAQUS软件中，计算结构非线性动态响应，形成预报水下近场爆炸载荷对结构毁伤效应的SPH-FEM模型，并基于该模型计算矩形板在近场爆炸载荷作用响应。

(2) 在近场爆炸载荷作用下，矩形板边缘为薄弱区域。在矩形板凹陷变形过程中四边受张力最大，其中长边中点最先达到强度极限。冲击因子较高时矩形板边缘在张力、剪切力共同作用下发生剪切破坏，易形成巨大破口，威胁结构物生命力。本文数值结果可为工程结构物抗爆抗冲击设计、评估提供参考。

参 考 文 献

[1] Ramajeyathilagam K, Vendhan C P. Deformation and rupture of thin rectangular plates subjected to underwater shock[J]. International Journal of Impact Engineering, 2004,30: 699-719.

[2] 姚熊亮,张阿漫,许维军. 声固耦合方法在舰船水下爆炸中的应[J]. 哈尔滨工程大学学报, 2005,26(6): 707-712.

YAO Xiong-liang, ZHANG A-man, XU Wei-jun. Application of coupled acoustic-structure analysisto warship underwater explosion[J].Journal of Harbin Engineering University, 2005,26(6): 707-712.

[3] 宗智,赵延杰，邹丽. 水下爆炸结构毁伤的数值计算[M]. 北京:科学出版社,2014.

[4] 朱锡,白雪飞,黄若波,等. 船体板架在水下接触爆炸作用下的破口试验[J]. 中国造船, 2003,44(1):46-52.

ZHU Xi,BAI Xue-fei,HUANG Ruo-bo,et al. Crevasse experiment research of plate membrance in vessels subjected to underwater contact explosion[J]. Shipbuilding of China, 2003,44(1): 46-52.

[5] 姚熊亮,张阿漫,许维军,等.基于ABAQUS软件的舰船水下爆炸研究[J]. 哈尔滨工程大学学报,2006,27(1):37-41.

YAO Xiong-liang, ZHANG A-man, XU Wei-jun, et al. Research on warship underwater explosion with ABAQUS software [J].Journal of Harbin Engineering University, 2006,27(1): 37-41.

[6] Geers T L,Hunter K S. An integrated wave-effects model for an underwater explosion bubble[J]. J. Acoust. Soc. Am., 2002,111(4): 1584-1601.

[7] 李金河,赵继波,谭多望,等. 炸药水中爆炸的冲击波性能[J]. 爆炸与冲击, 2009,29(2): 172-176.

LI Jin-he,ZHAO Ji-bo,TAN Duo-wang, et al. Underwater shockwave performances of explosive [J]. Explosion and Shock Waves, 2009,29(2): 172-176.

[8] Ming F R, Sun P N, Zhang A M.Investigation on charge parameters of underwater contact explosion based on axisymmetric SPH method [J]. Applied Mathematics and Mechanics, 2014,35(4): 453-468.

[9] Liu M B, Liu G R. Smoothed particle hydrodynamics (SPH): an overview and recent developments [J]. Archives of Computational Methods in Engineering, 2010,17(1): 25-76.

[10] Rajendran R, Paik J K, Lee J M. Of underwater explosion experiments on plane plates[J]. Experimental Techniques, 2007,31(1):18-24.

[11] Rajendran R, Narasimhan K.Performance evaluation of hsla steel subjected to underwater explosion [J]. Journal of Materials Engineering and Performance, 2001,10(1): 66-74.

[12] Liu G R, Liu M B. Smoothed particle hydrodynamics: a meshfree particle method [M]. World Scientific,2003.

[13] Colagrossi A,Landrini M. Numerical simulation of interfacial flows by smoothed particle hydrodynamics [J]. Journal of Computational Physics, 2003,191(2): 448-475.

[14] Benz W. Smoothed particle hydrodynamics: a review [J]. NATO Workshop, Les, Arcs, France, 1990,302:269-288.

[15] Zhang A M, Cao X Y, Ming F R, et al. Investigation on a damaged ship model sinking into water based on three dimensional SPH method [J]. Applied Ocean Research, 2013, 42: 24-31.

[16] 明付仁，张阿漫，杨文山，等. 舰船水下接触爆炸的SPH算法研究[J].振动与冲击, 2012, 31 (10): 147-151.

MING Fu-ren, ZHANG A-man, YANG Wen-shan, et al. SPH algorithm to deal with the problem of underwater contact explosion of warship [J]. Journal of Vibration and Shock, 2012, 31 (10): 147-151.

[17] 初文华,张阿漫,明付仁,等.SPH-FEM耦合算法在爆炸螺栓解锁分离过程中的应用[J].振动与冲击, 2012,31(23): 197-202.

CHU Wen-hua, ZHANG A-man, MING Fu-ren, et al. Application of three-dimensional SPH-FEMcoupling method in unlocking process of an explosion bolt [J]. Journal of Vibration and Shock, 2012, 31 (23): 197-202.

基金项目：国家自然科学基金资助(51279038；51479041)

收稿日期：2014-11-04修改稿收到日期：2014-12-26

中图分类号:U663；O383

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.02.021

Numerical investigation on near-field underwater explosion using SPH-FEM method

JIANG Zhong-tao1, WANG Lei2, SUN Peng-nan1, HUANG Xiao1

(1. College of Shipbuilding Engineering, Harbin Engineering University, Harbin 150001, China;2. Harbin Marine Boiler and Turbine Research Institute, Harbin 150001, China)

Abstract:The response of structures subjected to underwater shock wave is a highly nonlinear problem, the main difficulties of which are in the determination of the magnitude of shock wave load and the response of structures under transient load. Based on an improved axisymmetric Smoothed Particle Hydrodynamics (SPH) method, the near-field load of the underwater explosion was calculated and then it was used as the input to the FEM package ABAQUS. By using a coupled acoustic-structure model in ABAQUS, the nonlinear response of the structure was obtained. Based on the SPH-FEM model, the whole process of the near-field underwater explosion was simulated, starting from the detonation of the explosive charge to the large deformation, local tearing and complete damaging of the structure. The theoretical explanation of the axisymmetric SPH method was presented in detail and the calculated shock wave pressure load was validated by the experimental data. Then, the responses of rectangular plates subjected to near-field explosion were numerically investigated. The numerical results agree well with the experimental observations. Some useful conclusions regarding near-field explosion were drawn. The SPH-FEM model introduced here is robust and efficient, which is suitable for engineering applications.

Key words:ship engineering; rectangular plate; near-field explosion; SPH-FEM; structural damage

第一作者 姜忠涛 男，博士，高级工程师，1977年生