轴向运动功能梯度悬臂梁动力学分析

赵　亮， 胡振东

(同济大学 航空航天与力学学院，上海 200092)



轴向运动功能梯度悬臂梁动力学分析

赵亮， 胡振东

(同济大学 航空航天与力学学院，上海 200092)

摘要：针对轴向运动悬臂梁振动会影响系统的安全性、稳定性问题，对功能梯度悬臂梁振动特性进行分析，利用广义哈密尔顿原理及假设模态法导出系统动力学方程。结果表明，功能梯度悬臂梁的横向位移与轴向位移耦合，功能梯度材料在厚度方向按体积分数函数呈指数变化，且梁自由端有集中质量块。并讨论材料指数及末端集中质量大小对振动影响，分析梁在伸展、收缩时的运动特性。所得结论可为类似结构的动力学分析、设计提供依据。

关键词：功能梯度悬臂梁；轴向运动；振动分析；耦合的方程

轴向运动悬臂梁在工程中被广泛应用，如伸缩式机械手臂及卫星天线等。悬臂梁伸展过程中的振动对系统稳定性、安全性影响较大。因此颇受关注。如Wang等[1]利用牛顿力学方法建立轴向运动悬臂梁的控制方程，并用Galerkin法近似求解。Stylianou等[2]利用有限元法求解该问题时固定单元数目而单元长度随时间变化。Al-Bedoor 等[3]用有限元法分析在刚性旋转支座中作轴向运动的弹性机械手臂振动。Zhu 等[4]从能量角度分析轴向运动悬臂梁振动稳定性。Chang等[5]用有限元法分析轴向运动瑞利梁振动及稳定性。Wang等[6-7]利用广义哈密尔顿原理分析弹性及黏弹性梁的轴向运动特性。李山虎等[8]对伸展悬臂梁的独立模态振动控制进行理论近似解推导，并用多尺度方法进行求解。罗炳华等[9]建立轴向运动梁受移动载荷作用的有限元模型，提出描述运动梁节点约束状态的节点生死方法。刘宁等[10]推导移动质量作用的轴向运动悬臂梁振动方程，并用修正的Galerkin法对振动方程离散求解。陈红永等[11]针对Galerkin截断法计算轴向受载运动梁固有特性时低阶频率误差较大问题，引入轴向力对试函数进行改进，分析两端固支、固支-自由边界下Timoshenko梁的振动特性。

功能梯度材料(Functionally Gradient Materials, FGM)广泛用于机械制造、航空航天及土木工程。FGM为复合材料，上下表面各由一种材料制成，材料属性连续由一个表面变化到另一表面，故使其具有两种材料特性。关于FGM梁动力学分析文献较多[12-15]，而关于轴向运动FGM悬臂梁的文献较少。其利用有限元法分析轴向运动FGM悬臂梁振动时只考虑梁的横向振动位移。

本文利用广义哈密尔顿原理与假设模态法建立轴向运动FGM悬臂梁的动力学方程。考虑横向与轴向变形的耦合，分析该悬臂梁的运动特性。

1动力学方程建立

1.1功能梯度材料

本文研究的FGM由陶瓷与金属制成，其有效材料属性P(P代表弹性模量E，泊松比υ及密度ρ)在材料厚度方向按各组分体积分数函数连续变化，表示为

P=PTVT+PBVB

(1)

式中：PT，PB为梁上、下表面材料属性；VT，VB为上、下表面材料体积分数，即

VT+VB=1

(2)

FGM的有效材料属性用幂函数定义。梁上部组分体积分数为

(3)

式中：k为非负参数(幂函数指数)，控制材料属性沿梁厚度方向变化趋势。

由式(1)～式(3)可得FGM梁的有效材料属性为

(4)

由式(4)知，z=-h/2时P=PB，z=h/2时P=PT。

1.2控制方程建立

轴向运动FGM悬臂梁见图1。梁初始长度为L0，长度L(t)随时间变化。轴向运动速度v的正负表示梁处于伸展或收缩状态。分析中加速度恒定，集中质量块mtip位于梁末端。梁任意点x处轴向、横向振动位移分别用w(x,t)、u(x,t)表示。梁刚性支撑部分无弹性变形。梁厚度、宽度分别用h、b表示。

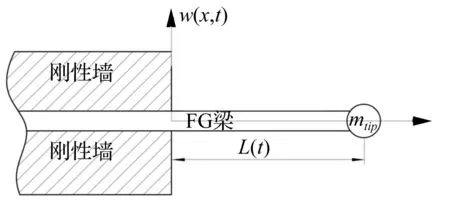
图1　轴向运动功能梯度悬臂梁Fig.1 An axially translating FG cantilevered beam

基于伯努利-欧拉薄梁理论及小挠度假设, 梁的轴向正应力、应变分别为

(5)

式中：E为梁的弹性模量。

系统动能可表示为

(6)

系统势能为

(7)

式中：P为梁的轴向张力，可表示为

(8)

将式(5)代入(6)、(7)，得

(9)

(10)

式中：

结构动力学方程通过广义哈密尔顿原理与假设模态法获得。广义哈密尔顿原理表示为

(11)

对自由振动问题δW=0。运动过程中梁长随时间变化。为便于分析，用参数ξ=x/L(t)将空间区域[0,L(t)]投影到单位区间[0,1]上。梁的横向振动位移可用广义坐标及模态函数表示，即

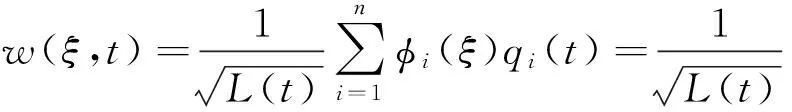
(12)

式中：[φ]=[φ1(ξ),…,φn(ξ)]；{q}=[q1(t),…,qn(t)]。

悬臂梁横向振动模态函数为

φi(ξ)=[cosh(λiξ)-cos(λiξ)]-

(i=1,2,…,n)

(13)

式中：λi为参数，由特征方程获得，即

1+cosh(λi)cos(λi)=0,(i=1,2,…,n)

(14)

类似，轴向振动位移可表示为

(15)

式中：[ψ]=[ψ1(ξ),…,ψn(ξ)]；{r}=[r1(t),…,rn(t)]。

对悬臂梁

(16)

将式(12)、(15) 分别代入式(9)、(10)，系统的动能T与势能U可表示成关于广义坐标及模态函数的表达式。再将T、U代入式(11),对变量r、q进行变分运算，所得系统动力学方程为

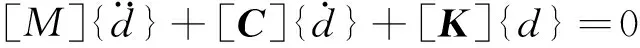
(17)

式中：

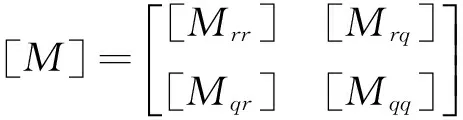
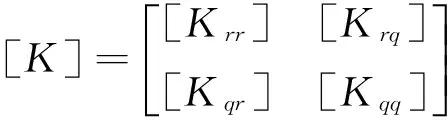
以上各矩阵表达式较复杂，见附录。求解式(17)可获得系统的动力响应。

2数值算例分析

为验证所建动力学方程的正确性，将计算结果与文献[3]进行对比。所用参数为：弯曲刚度EI=756.65 Nm2，单位长度质量ρA=4.015 kg/m,轴向运动速度v=0.3 m/s，梁初始长度L0=1.8 m，自由端初始挠度w(L0,0)=-0.005 m。计算结果见图2。可见本文结果与文献[3]结果一致，从而验证本文动力学方程的正确性。

利用算例分析FGM悬臂梁的轴向运动特性。FGM

梁上部材料为铝，E=70 GPa，ρ=2 700 kg/m3,υ=0.23；下部材料为氧化铝，E=380 GPa,ρ=3 800 kg/m3,υ=0.23。梁宽b=0.2 m, 高h=0.01 m。运动方程用Newmark法求解。

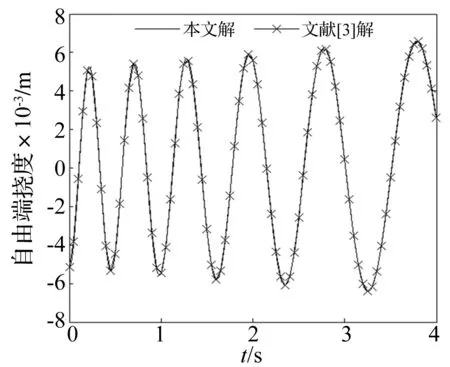
图2　L(t)=1.8+0.3t时轴向运动悬臂梁自由端挠度Fig.2 Tip deflection of the axially translating beam when L(t)=1.8+0.3t

分析材料指数k及末端质量对FGM梁轴向运动影响。FGM梁上部材料体积分数沿厚度方向变化曲线见图3。由图3看出，k越大梁的材料属性由上部向下部过渡越快，梁的刚度越大，梁振动频率越大变形越小。

不同指数k时梁自由端挠度曲线见图4。给定轴向运动速度1 m/s, 末端质量1 kg, 梁初始长度1 m，自由端横向初速度0.001 m/s。由图4看出，k越大梁振动频率越大，振幅越小。

不同末端质量梁自由端挠度曲线见图5。给定k=0.1，末端质量分别为0、1 kg、2 kg、3 kg，其它参数同前。可见末端质量越大梁振动频率越小，振幅越大。

图3 FGM梁上部材料体积分数沿厚度方向的变化Fig.3VariationofthevolumefractionoftheupperconstituentVTthroughthethicknessoftheFGMbeam图4 不同指数k的梁自由端挠度Fig.4Tipdeflectionsunderdifferentpower-lawexponent图5 不同末端质量的梁自由端挠度Fig.5Tipdeflectionsunderdifferenttipmass

分析FGM梁在伸展、收缩时的运动特性。计算参数为：k=0.1，末端集中质量1 kg, 自由端横向初速度1 m/s，梁伸展时初始长度1 m，伸展速度0.5 m/s。计算结果见图6。由图6看出，梁伸展过程中，自由端横向振幅逐渐增大而轴向振幅逐渐减小。梁振动总能量随其伸长而减小，说明系统在稳定状态。梁收缩时初始长度3 m，收缩速度-0.5 m/s，计算结果见图7。由图7看出，梁收缩时自由端横向振幅逐渐减小而轴向振幅逐渐增大。振动总能量随其收缩逐渐增大，说明系统处于不稳定状态。

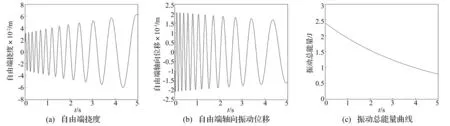
图6　L(t)=1+0.5t时轴向运动FGM悬臂梁Fig.6 Axially translating FGM beam when L(t)=1+0.5t

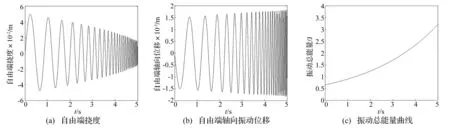
图7　L(t)=3-0.5t时轴向运动FGM悬臂梁Fig.7 Axially translating FGM beam when L(t)=3-0.5t

3结论

(1) FGM梁材料指数能规定其材料属性由上部组份向下部组份变化的快慢。指数越大材料属性变化越快，梁刚度越大，振动频率越大而振幅越小。末端集中质量越大梁振动频率越小，振幅越大。

(2) FGM梁伸展过程中自由端横向振幅逐渐增大，轴向振幅逐渐减小，振动总能量随梁伸长而减小时系统为稳定状态；收缩时自由端横向振幅逐渐减小，轴向振幅逐渐增大，振动总能量随梁收缩而逐渐增大时系统处于不稳定状态。

参 考 文 献

[1] Wang P K C, Wei J D. Vibrations in a moving flexible robot arm [J]. Journal of Sound and Vibration, 1987,116(1):149-160.

[2] Stylianou M, Tabarrok B. Finite element analysis of an axially moving beam,part I-time integration [J]. Journal of Sound and Vibration,1994,178(4):433-453.

[3] Al-Bedoor B O, Khulief Y A. Finite element dynamic modeling of a translating and rotating flexible link[J]. Computer Methods in Appalled Mechanics and Engineering, 1996, 131:173-189.

[4] Zhu W D, Ni J. Energetic and stability of translating media with an arbitrarily varying length [J]. ASME Journal of Vibration and Acoustics, 2000,122(3):295-304.

[5] Chang J R, Lin W J, Huang C J, et al. Vibration and stability of an axially moving Rayleigh beam [J]. Applied Mathematical Modelling, 2010, 34(6):1482-1497.

[6] Wang L H, Hu Z D, Zhong Z, et al. Hamiltonian dynamic analysis of an axially translating beam featuring time-variant velocity [J]. Acta Mechanic, 2009, 206:149-161.

[7] Wang L H, Hu Z D, Zhong Z, et al. Dynamic analysis of an axially translating viscoelastic beam with an arbitrarily varying length [J]. Acta Mechanic, 2010, 214:225-244.

[8] 李山虎,杨靖波,黄清华,等. 轴向运动悬臂梁的独立模态振动控制(I)近似理论分析[J].应用力学学报,2002,19(1):35-38.

LI Shan-hu, YANG Jing-bo, HUANG Qing-hua, et al. Independent model space vibration control of an axially moving cantilever beam (part I) theoretical analysis of approximation [J]. Chinese Journal of Applied Mechanics, 2002, 19(1):35-38.

[9] 罗炳华,高跃飞,刘荣华,等．轴向运动梁受移动载荷作用的横向动力响应[J]. 振动与冲击,2011, 30(3):59-63.

LUO Bing-hua, GAO Yue-fei, LIU Rong-hua, et al. Lateral dynamic response of an axially moving beam under a moving load [J]. Journal of Vibration and Shock, 2011, 30(3):59-63.

[10] 刘宁,杨国来. 移动质量作用下轴向运动悬臂梁振动特性分析[J]. 振动与冲击,2012, 31(3):102-105.

LIU Ning, YANG Guo-lai. Vibration property analysis of axially moving cantilever beam considering the effect of moving mass[J]. Journal of Vibration and Shock,2012,31(3):102-105.

[11] 陈红永，陈海波，张培强.轴向受压运动梁横向振动特性的数值分析[J]. 振动与冲击，2014, 33(24): 101-105.

CHEN hong-yong, CHEN Hai-bo,ZHANG Pei-qiang.Numerical analysis of free vibration of axially moving beam under compressive load[J]. Journal of Vibration and Shock, 2014, 33(24): 101-105.

[12] Piovan M T, Sampaio R. Vibrations of axially moving flexible beams made of functionally graded materials [J]. Thin-Walled Structures, 2008, 46(16): 112-121.

[13] Kang Y A, Li X F. Bending of functionally graded cantilever beam with power-law non-linearity subjected to an end force [J]. International Journal of Non-Linear Mechanics, 2009, 44(6): 696-703.

[14] Simsek M. Vibration analysis of a functionally graded beam under a moving mass by using different beam theories[J]. Composite Structures, 2010, 92: 904-917.

[15] Pradhan K K, Chakraverty S. Free vibration of Euler and Timoshenko functionally graded beams by Rayleigh-Ritz method [J]. Composites: Part B, 2013, 51:175-184.

附录

式(17)中矩阵[M],[C],[K]的各元素表达式为

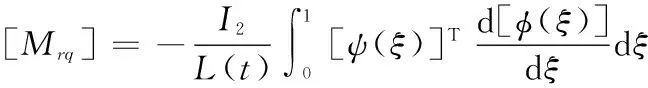
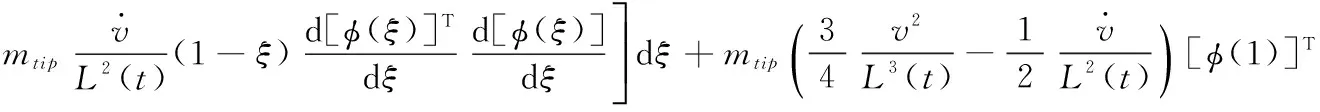
式中：

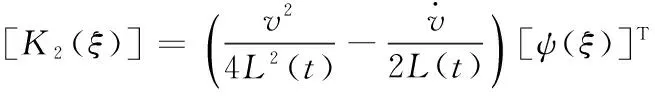
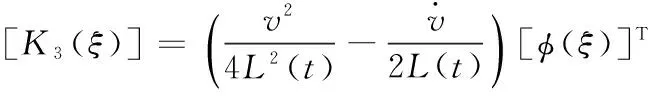
基金项目：国家高技术研究发展计划 863 项目 (2012AA041804)

收稿日期：2014-10-16修改稿收到日期：2015-01-30

通信作者胡振东 男，教授，博士生导师，1964 年生

中图分类号:TH212；TH213.3

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.02.020

Dynamic analysis of an axially translating functionally graded cantilever beam

ZHAO Liang, HU Zhen-dong

(School of Aerospace Engineering and Applied Mechanics, Tongji University, Shanghai 200092, China)

Abstract:The axially translating cantilever beams are widely used in engineering. The vibration of the beams will exert great effect on the safety and reliability of the system. An axially translating functionally graded (FG) cantilevered beam was dynamically analysed. The equations of the system were derived according to the Hamilton’s principle by using the assumed mode method. And the coupled equations of motion were gotten. The properties of the FG material were functionally graded in the thickness direction according to the volume fraction power-law distribution. A tip mass was considered to be concentrated at the free end of the beam. The effects of the power-law material exponent and tip mass on the vibration were discussed. Moreover, the movement characteristics of the FG beam during the extension mode and the retraction mode were analyzed. The conclusions give a basis for dynamic analysis and design of similar structures.

Key words:functionally graded cantilevered beam; axially translating; dynamic analysis; coupled equations

第一作者 赵亮 男，博士生，1981年生

邮箱: zdhu@tongji.edu.cn