频响函数曲线拟合与模态分析精细化

董　磊， 宋汉文， 郑铁生

(1.复旦大学 力学与工程科学系，上海　200433； 2.同济大学 航空航天与力学学院，上海　200092)



频响函数曲线拟合与模态分析精细化

董磊1， 宋汉文2， 郑铁生1

(1.复旦大学 力学与工程科学系，上海200433； 2.同济大学 航空航天与力学学院，上海200092)

摘要：由于Vector Fitting (VF)将有理分式函数直接分解为部分分式和的叠加，极点(模态频率)获取顺序依模态贡献量由大到小排列，可保证拟合误差随拟合阶次增大迅速收敛，故对VF方法用于模态参数辨识的可行性进行论证，优化拟合精度与计算规模，并对曲线拟合算法误差、参数稳定性、模型定阶详细讨论，实现频响函数曲线拟合的精细化。利用已有文献数据进行考核，并与商业算法比较。

关键词：模态分析；参数辨识；频率响应函数；曲线拟合；精细化

目前，振动模态分析与参数辨识技术已形成完整的理论体系，广泛用于航空、航天、舰船、机械、汽车、土木等工程领域。实验模态分析(Experiment Modal Analy-sis，EMA)中大部分频域算法均存在曲线拟合精度的困难。随技术学科应用推动，模态参数辨识面临更高要求，即对曲线拟合精度精细化及对算法在不同阶次的参数稳定性。

传统频响函数确定有理分式多项式阶次及部分分式系数(即各阶模态系数)拟合存在较多困难，拟合误差过大，能达到的最小误差亦无法满意，严重影响模态参数的辨识精度。随阶次增高会使数值不稳定、计算量增大等，导致模态辨识失败，转而进行分段拟合，致模态密度愈高的频响函数，辨识结果愈加下降。

算法模型阶次选择难题亦会导致模态参数筛选时强烈的人工依赖性。如正交多项式[1]、LSCE[2]等选择不同阶次下所得模态参数不具有可比性，且在拟合过程中需确定合适阶次。为提高参数精确性及人工经验在不同阶次下模态挑选，除具有良好的曲线拟合精度、收敛误差外，亦需具有良好的稳定性，即在不同阶次下所得参数稳定。

Vector Fitting(VF)[3]原用于解决电力传输模型中频率响应函数拟合，现已得到改进。如Relaxed Vector Fitting(RVF)[4]可提升VF算法极点重分布能力，降低初始极点选择的重要性；Orthonormal Vector Fitting(OVF)[5-7]使拟合方程条件数得以改善，并降低迭代步数及总机时，增强算法的稳定性。Hendrickx等[8]证明VF方法为Sanathanan-Koerner (SK)迭代过程，并将原始VF与OVF统一。Deschrijver等[9]提出Relaxed Orthonormal Vector Fitting(ROVF)，同时结合RVF与OVF的优点。Grivet-Talocia等[10]用Vector Fitting with Adding and Skimming(VF-AS)算法提高数据含噪声的收敛性并对模型阶次及参数选择设定判据。对多曲线拟合，Deschrijver等[11]采用QR分解曲线拟合方程，解决多曲线拟合时系数矩阵稀疏性及效率低下问题。Mekonnen等[12]将VF方法引入z域，建立ZD-VF方法。Grivet-Talocia等[13]将VF方法引入时域，建立Time Domain Vector Fitting(TD-VF)在时域内直接用原始激励、响应信号进行曲线拟合。Haegeman等[14]将正交基引入时域。Moon等[15]将频、时域数据混合拟合。Lei等[16]将VF方法用于离散时间系统参数识别。Ubolli等[17]将ZD-VF、TD-VF及ARMA方法进行比较。Lefteriu等[18]对VF方法的收敛性进行论述。

电力传输系统中，主要目的为提取等效模型，对参数分析、筛选并不关注。在振动模态参数辨识领域，参数辨识方法需面对更进一步误差分析、参数筛选及模型阶次规则改变。

本文简要综述VF方法及其主要改进，并论证各项改进在模态参数辨识中的适用性，证明VF方法基函数的最优化，构造出用于振动模态参数辨识的频率响应函数拟合算法，并实验及算例考核。

1Vector Fitting算法基础

对有理函数形式的待辨识曲线，未知参数同时包含在分子、分母中，即

(1)

式中：br为极点；ar为零点；ur为留数；vr为高次项系数。

VF方法将R(s)的分子分母同除与分母同阶的多项式T(s)，该多项式初始极点pr人为设定，称极点替换函数，即

(2)

则R(s)变为

(3)

将式(3)分母乘以等式两边得

(4)

l2n=span(φ1(s),…φ2n(s))

(5)

于是有

(6)

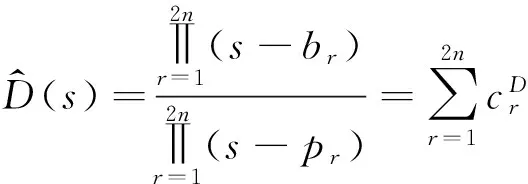
(7)

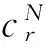
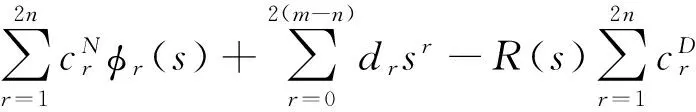
原始VF方法，取基函数为

(9)

式(8)可表示为

(11)

式中：Qr(s)为r-1阶多项式。

(12)

式(8)可写为

(13)

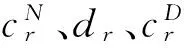
(14)

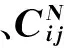
式中：nc为曲线总数。

一般而言，方程(15)系数矩阵巨大、稀疏，计算效率低。而实际只需求出含系统极点信息的CD， Deschrijver利用QR分解为上三角矩阵，式(14)变为

(16)

方程缩减为

(17)

由此可解决多曲线拟合中效率低的问题。

(18)

2VF方法在模态参数辨识中的改进

模态参数辨识中，线性时不变系统频响函数为有理分式多项式，取s=jω，其形式为

(19)

式中：λr为系统极点；zij,r为零点；Rij,r为留数。

若Hij(ω)为位移频响，则m=n-1，cij=0；若为加速度频响，则m=n，cij为常数。实际拟合中数据总在有限频段内，因而可将模态频率是否在数据段内分为

(20)

当数据段外模态固有频率Re(λr)≫ω，上式第二项可近似为

(21)

式(21)为一复常数项，即在位移频响中，考虑对高频剩余模态补偿，也可用m=n模型。

将Hij(ω)代入式(8)，简化为

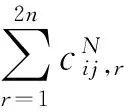
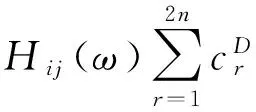
(22)

式(14)简化为

(23)

VF系统模型允许模态分析中频响函数分子与分母有更多阶次关系，因而适用范围更广。模态参数辨识中，拟合的数据对象可为位移频响函数、加速度频响函数、广义传递率函数、功率谱密度函数，广泛适用于实验及工况模态分析。与在对极点参数筛选后才能对高频剩余模态补偿方法不同，VF在获取极点过程中系统模型即可对剩余模态进行补偿。

拟合中因存在误差及噪声，导致数据中存在非系统模态，而拟合非系统模态能提高曲线拟合精度及系统模态参数精度。部分系统模态能量可能小于非系统模态，故会晚于非系统模态被拟合。因此，无论拟合精度或系统模态参数完全性均要求阶次高于系统模态数。由于数据信噪比及模态能量间不均衡性，系统模态可能因不符合能量准则被舍去。而若测点在某阶模态节点附近，则其能量在频响中必较小，故VF-AS据能量进行模态筛选准则并不合适，基于最小模型原则的定阶准则对密集模态辨识也极为不利。

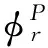
(24)

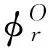
(25)

为进一步提高矩阵正交性改善拟合方程条件数，将正交基的内积空间定义在数据频段(ω1,ω2)上。因数据的离散化，内积定义为

(26)

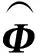
(27)

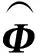
无论OVF对基函数理论正交化或基于式(26)的数值正交化，实质上均对矩阵方程(24)的不完全正交化，而QR分解则对式(24)整个矩阵完全正交化。

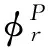
考虑算法及实际编程的统一性， RVF加QR分解算法在精度、效率上最优，称为Relax QR Vector Fitting，此为本文所用最终实现算法。

3实验考核

为考核VF方法的辨识精度及稳定性，本文采用加拿大RADARSAT-I卫星实验模态数据[19]进行分析。该数据频响曲线复杂、模态丰富密集，在49～52 Hz频段内有10个密集模态[20]，辨识难度较高，见图1。实验具体描述可从相关网站获得，频响中感兴趣的频段为10～64 Hz。拟合过程中，拟合频段取0～64 Hz。由于无任何一条频响包含所有模态，故选其中一条模态峰值丰富的单曲线显示VF方法拟合精度及误差收敛规律。通过多曲线拟合获得全部模态，利用多曲线稳态图显示VF方法模态参数获取能力及参数稳定性。并通过稳定模态参数提取重构频响显示VF方法最终的参数辨识精度。

3.1曲线拟合精度

通过尝试，选模态丰富的nsar:420+X/pms:217-X曲线演示VF方法曲线拟合所达精度及误差随阶次变化规律。VF方法选择各种初始极点鲁棒性较好。为更好符合实际系统，初始极点选共轭复极点，虚部均匀分布于拟合频段，实部为负数，大小为虚部的1%。取阶次100的拟合曲线见图2。由图2看出，VF方法曲线拟合能力较强，无需对频段分段拟合下可获得高精度拟合效果，一次性得到曲线中所有模态。

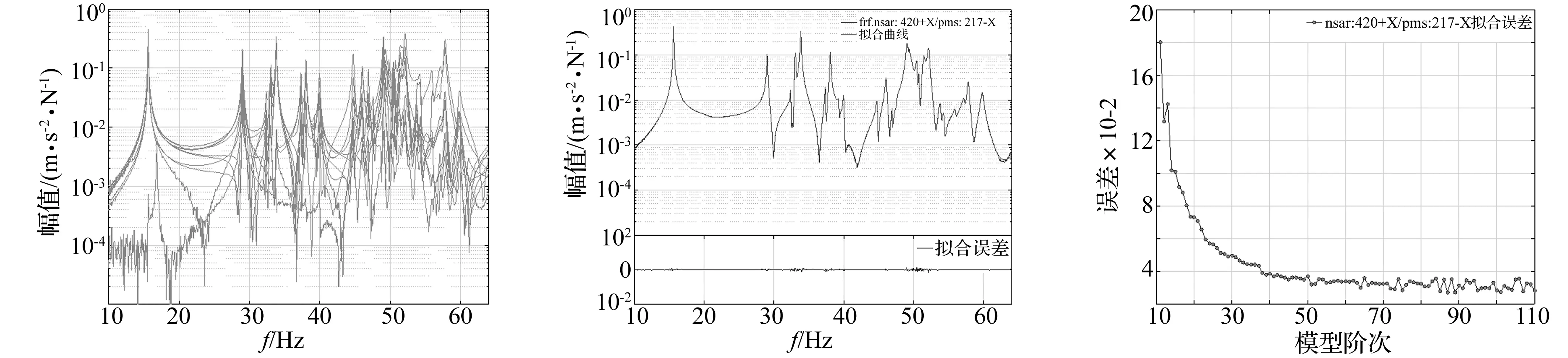
图1 复杂且模态密集的频响函数Fig.1ComplexFRFSwithcloselyspacedmodes图2 nsar:420+X/pms:217-X曲线拟合精度Fig.2FittingPrecisionofFRFnsar:420+X/pms:217-X图3 nsar:420+X/pms:217-X曲线拟合误差Fig.3ErrorchartforincreasingmodelorderofFRFnsar:420+X/pms:217-X

实验中大多采用加速度传感器，所得为加速度频响函数。而VF可用分子与分母具有相同阶次多项式模型进行拟合，即VF方法可采用更精确的频响函数模型。且分子分母具有相同阶次模型不仅更符合加速度频响模型，更可对高阶剩余模态进行补偿。

3.2参数稳定性讨论

曲线拟合精度为模态参数辨识基础，高质量曲线精度能保证参数辨识精度。参数筛选则依赖算法参数的稳定性。模态参数辨识中，稳态图为最有效的模态参数筛选工具。为提取模态参数，需设定判据对模态稳定性判别。对模态稳定模态判定指标为频率误差0.2 Hz，阻尼、模态能量误差10%。

曲线稳态见图4。由图4看出，VF方法参数提供的稳定模态分布清晰直观。随模型阶次增加峰值处模态参数不仅与前一阶次保持误差范围内的稳定性，且在模型阶次遍历过程中均有一致稳定性，在模型阶次提高过程中不存在偏移。

表1为据图4提取的49～52 Hz频段内密集模态处参数。可见，无论阶次低于获高于系统模态数时，VF方法所得参数均具有较高统一性。不因模型阶次不同而不稳定。在此条曲线上未含全部10个密集模态。

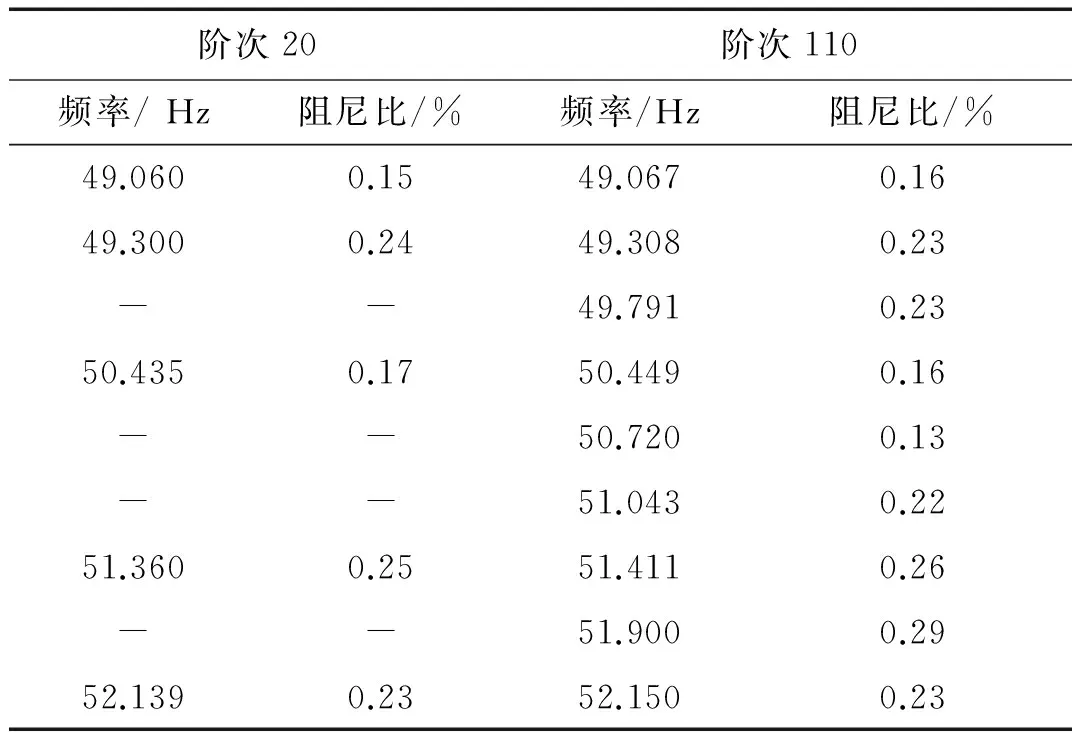
表1　不同阶次频段模态参数对比

VF方法在峰值附近的模态密度明显大于其它频率处。图5为单曲线的局部放大图，可见单曲线模态峰值周围模态密集处数据中误差形成的数值模态也有稳定性。如15～16 Hz频段出现4个稳定模态，但仅最早出现的15.617 Hz模态为系统模态。

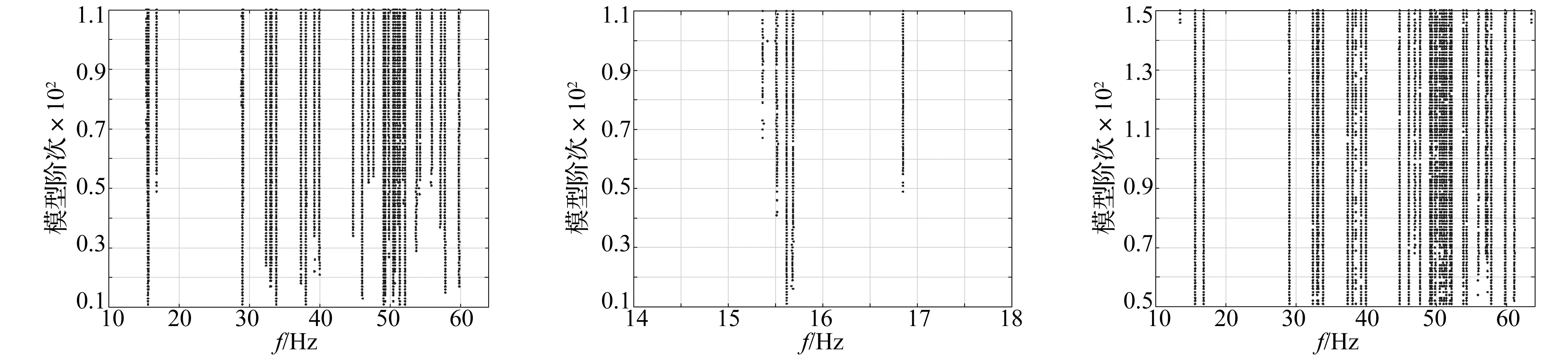
图4 单曲线稳态图Fig.4Stabilizationdiagramsobtainedbysinglecurvefitting图5 单曲线稳态图局部Fig.5Localamplificationofstabilizationdiagramsobtainedbysinglecurvefitting图6 多曲线稳态图Fig.6Stabilizationdiagramsobtainedbymulti-curvefitting

系统模态与数值模态参数见表2。由表2看出，模态密集处真实系统模态较数值模态在留数上有数量级的差别，因数值模态与系统密集模态不同。与系统密集模态不同的另一点即密集在峰值附近由曲线中独有误差形成的稳定模态不具有普遍性，多曲线拟合时会消失。误差在不同曲线间存在差异性，会造成单曲线拟合精度高于多曲线。数值模态稳定出现说明VF方法曲线精度较高。

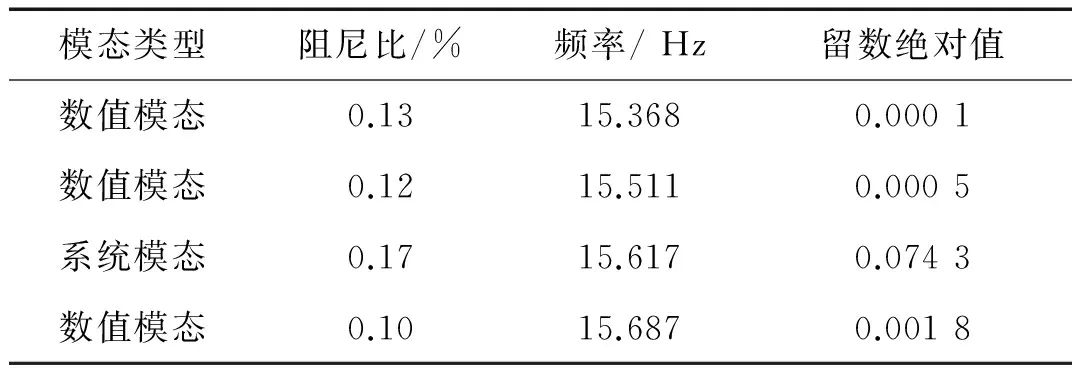
表2　系统模态与数值模态参数

由多曲线拟合所得整体模态稳态图见图6。由图6看出，VF多曲线拟合的模态参数仍保持高度稳定性，该稳定性能极大减小模态参数选择难度及经验的依赖性，提高模态筛选过程中客观化程度，甚至为进一步自动选择奠定良好基础。

3.3模态参数挑选

由于VF方法拟合误差的收敛性及模态参数稳定性，利用VF方法进行模态参数辨识不再依赖模型阶次的确定。拟合误差稳定后稳定模态基本不再变化。可从其中挑选一个阶次的参数，或取多个阶次的平均值。

利用稳态图对系统模态参数筛选后，用所得模态频率、阻尼进行线性拟合，获得最终重构频响函数用以显示VF方法最终所达曲线精度及参数精度。模态参数取120～140阶次的平均值。重构频响见图7。由图7看出，无论幅值或相位均达到较高精度，表明不稳定模态在能量上较小。

图7　nsar:420+X/pms:217-X重构频响Fig7 FRF of nsar: 420+X/pms: 217-X Synthesized from the Identified Modal Parameters

3.4与PloyMAX结果对比

PloyMAX算法具有较高的辨识精度及稳定性。原理如下：

对具有No个输出、Ni个输入系统，其频响矩阵H(ω)∈CNo×Ni可表示为

H(ω)=B(ω)A-1(ω)

(28)

B(ω)∈CNo×Ni，A(ω)∈CNi×Ni分别为

(29)

式中：Ωr(ω)=exp(-iωΔtr)为基函数；Δt为采样间隔；n为模型阶次；Ar，Br为矩阵多项式系数。

通过对式(28)右乘 A(ω)进行线性化处理，利用最小二乘法求解系数矩阵。在求出分母多项式系数Ar基础上对扩展矩阵进行SVD分解，可得极点及模态参与因子，即

(30)

将49～52 Hz频段的VF结果与PloyMAX算法对RADARSAT-I卫星辨识结果对比，见表 3。由表3看出，VF方法与PolyMAX算法精度相同。

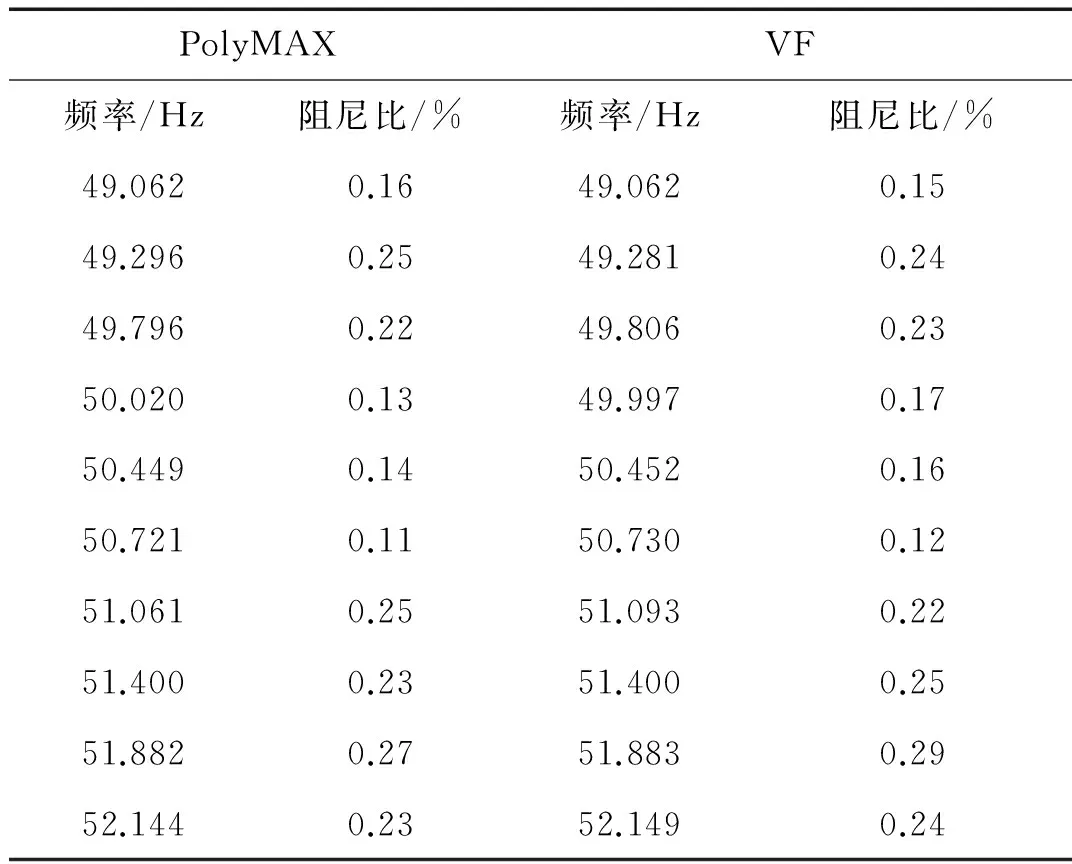
表3　模态参数对比

4结论

通过将VF方法用于模态参数辨识，对其各种改进进行综合并据模态分析需要进行分析取舍，确定RVF及结合QR分解精度、效率的最优性；并对模态参数辨识中曲线精度、拟合误差、参数稳定性及参数筛选深入分析，对含多个密集模态的卫星数据进行辨识并与顶尖商业算法对比，验证VF方法模态辨识能力。结论如下：

(1) 采用分子分母相同阶次模型能更符合加速度频响模型，获取极点过程中即可补偿高频剩余模态。

(2) VF方法无需划分频段，即可对曲线进行一次性拟合，从而能减小工作量及划分不当导致参数稳定性、精度下降。

(3) 随模型阶次增加误差迅速收敛，不会因模型阶次选择不当导致曲线精度下降。

(4) 无论低、高阶次下所得参数均稳定，从而能减小对模型阶次的依赖性，提高模态参数准确性、确定客观化及选择速度。

(5) VF方法可面对复杂的频响特性，实现精细化拟合的同时降低人工操作依赖性，增强客观化，为曲线拟合及模态参数辨识的新方法。

参 考 文 献

[1] Formenti D, Richardson M, Spie S. Parameter estimation from frequency response measurements using rational fraction polynomials (twenty years of progress)[J]. In Proceedings of Imac-Xx: Structural Dynamics,2002, I:373-382.

[2] Brown D L, Allemang R J,Zimmerman R,et al. Parameter estimation techniques for modal analysis[C]// Commonwealth Drive, Warrendale,United States: SAE International,1979.

[3] Gustavsen B, Semlyen A. Rational approximation of frequency domain responses by vector fitting[J]. Power Delivery, IEEE Transactions on, 1999,14(3): 1052-1061.

[4] Gustavsen B. Relaxed vector fitting algorithm for rational approximation of frequency domain responses[C]//Signal Propagation on Interconnects, IEEE Workshop on,2006.

[5] Deschrijver D, Dhaene T. Broadband macromodelling of passive components using orthonormal vector fitting[J]. Electronics Letters, 2005,41(21):1160-1161.

[6] Deschrijver D, Dhaene T. Rational modeling of spectral data using orthonormal vector fitting[C]//Signal Propagation on Interconnects, Proceedings 9th IEEE Workshop on,2005.

[7] Deschrijver D, Haegeman B, Dhaene T. Orthonormal vector fitting: a robust macromodeling tool for rational approximation of frequency domain responses[J]. Advanced Packaging, IEEE Transactions on, 2007,30(2):216-225.

[8] Hendrickx W, Dhaene T. A discussion of “rational approximation of frequency domain responses by vector fitting”[J]. Power Systems, IEEE Transactions on, 2006, 21(1):441-443.

[9] Deschrijver D, Gustavsen B, Dhaene T.Advancements in iterative methods for rational approximation in the frequency domain[J]. Power Delivery, IEEE Transactions on, 2007, 22(3):1633-1642.

[10] Grivet-Talocia S, Bandinu M. Improving the convergence of vector fitting for equivalent circuit extraction from noisy frequency responses[J]. Electromagnetic Compatibility, IEEE Transactions on, 2006,48(1):104-120.

[11] Deschrijver D, Mrozowski M, Dhaene T, et al. Macromodeling of multiport systems using a fast implementation of the vector fitting method[J]. Microwave and Wireless Components Letters, IEEE, 2008,18(6): 383-385.

[12] Mekonnen Y S, Schutt-Aine J E. Broadband macromode-ling of sampled frequency data using z-domain vector-fitting method[C]//Signal Propagation on Interconnects, SPI, IEEE Workshop on,2007.

[13] Grivet-Talocia S. Package macromodeling via time-domain vector fitting[J]. Microwave and Wireless Components Letters, IEEE, 2003,13(11): 472-474.

[14] Haegeman B, Deschrijver D, Dhaene T. Efficient time-domain macromodeling of complex interconnection structures[C]//Eurocon, International Conference on & #34;Computer as a Tool & #34,2007.

[15] Se-Jung M, Cangellaris A C. Rational function fitting of electromagnetic transfer functions from frequency-domain and time-domain data[C]//Microwave Symposium Digest, IEEE MTT-S International,2006.

[16] Chi-Un L, Ngai W. Efficient linear macromodeling via discrete-time time-domain vector fitting[C]//VLSI Design, VLSID,21st International Conference on,2008.

[17] Ubolli A, Gustavsen B. Comparison of methods for rational approximation of simulated time-domain responses: ARMA, ZD-VF, and TD-VF[J]. Power Delivery, IEEE Transactions on, 2011,26(1): 279-288.

[18] Lefteriu S,Antoulas A C.On the convergence of the vector-fitting algorithm[J]. Microwave Theory and Techniques, IEEE Transactions on, 2013,61(4):1435-1443.

[19] Modal parameter estimation round robin[R].Available from: http://www.me.mtu.edu/imac_mpe/MPE Radarsati Data Description.htm,2011.

[20] Peeters B, Pauwels S, Debille J. Enhanced exploitation of vibration test data by the polymax modal parameter estimation method[C]//5th International Symposium on Environmental Testing for Space Programmes, Noordwijk, Netherlands: European Space Agency, 2004.

基金项目：国家自然科学基金(11272235)

收稿日期：2015-01-04修改稿收到日期：2015-02-03

通信作者宋汉文 男，教授，博士生导师，1961年生

中图分类号:O321;O327

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.02.012

Refinement of FRFs curve fitting and modal analysis

DONG Lei1, SONG Han-wen2, ZHENG Tie-sheng1

(1. Department of Mechanics and Engineering Science, Fudan University, Shanghai 200433, China; 2. School of Aerospace Engineering and Applied Mechanic, Tongji University, Shanghai 200092, China)

Abstract:In conventional orthogonal polynomial algorithms which are most widely used in modal analysis, the best model order is usually defined with the consideration of the existence of the noise modes. Unfortunately, the minimum error could not be well achieved simultaneously. Considering the numerical instability and the computation difficulty due to the increase of model order, the demand of dividing the frequency range into several sub-bands comes up. The vector fitting (VF) algorithm was introduced to decompose the rational function by taking common set of partial fractions as basis functions, and the acquisition order of the modes was arranged according to the modal energy, to ensure the fast convergence of VF algorithm. Then, the parametric stability of the partial fractions and the numerical stability can be attained with the increase of the model order. In the paper, a brief review of VF was presented and the feasibility of VF in modal analysis was demonstrated. The refinement of the FRFs curve fitting was completed through a fine disposal of deviation analysis, parametric stability and order selection. An aerospace case study was carried out to verify the effectiveness of the algorithm and the results were compared with those by another algorithm.

Key words:modal analysis; parameter identification; FRFs; curve fitting; refinement

第一作者 董磊 男，博士生，1985年生