威布尔分布风速下基于遗传算法的风力机叶片优化设计

李帅斌, 王　昊, 范海哲

(上海电力学院 能源与机械工程学院, 上海　200090)



威布尔分布风速下基于遗传算法的风力机叶片优化设计

李帅斌, 王昊, 范海哲

(上海电力学院 能源与机械工程学院, 上海200090)

考虑了风速的威布尔(Weibull)分布,以年发电量最大为目标函数,运用遗传算法对某1.5 MW风力发电机叶片的气动性能进行了优化设计:将叶片沿展向分为13段,以每段的功率作为遗传算法的适应度函数.优化所得的气动外形参数体现了比Wilson方法和额定风速下的遗传算法更为合理的结果,弦长和扭角更趋于流线型分布,且扭角整体呈减小的趋势.

风力机叶片; 威布尔分布; 遗传算法; 优化设计

叶片是风力机最为关键的零部件之一,其设计涉及复杂的寻优搜索过程[1].设计性能良好的风力机叶片必须满足多项技术指标,其中某些指标之间会相互制约,因此优化设计技术在叶片的设计制造中占有相当重要的地位,气动外形的优劣直接影响叶片整体的最优体型设计.

初期风力机叶片优化设计方法主要是Glauert方法和Wilson方法[2-3].杨涛等人基于叶素-动量理论,通过Wilson设计方法对1.2 MW风力机叶片进行了优化设计,并对叶片进行了三维实体建模[4].傅洁等人以片条理论为基础,采用遗传算法对额定风速7.5 m/s下的叶片进行了优化设计,该设计虽然克服了Wilson优化设计方法的不足,但仅得到在额定风速下使功率达到最大的结果[5].上述研究没有考虑实际风速的概率密度分布,相对全年而言,风力机在大部分时间内并非在额定风速下运行,因此以考虑威布尔风速分布下的年发电量为目标函数的数学模型更具有现实意义.另外,由于普通的非智能算法——Wilson方法所得到的弦长c和扭角θ呈现出一定的非线性分布[6],经过修正后,在叶根部分仍会出现突变,得到的并非全局最优解,因此采用智能算法中的遗传算法,对弦长和扭角进行寻优,所得到的结果更具合理性[7].鉴于此,本文在考虑Weibull分布风速下,采用遗传算法对叶片进行了优化设计.

1　叶片气动分析设计模型

片条理论[8-9]综合考虑了风力机叶片基本设计理论中的叶素理论和动量理论,修正后得到的轴向和切向诱导因子分别为:

(1)

(2)

式中:a,b——轴向和切向诱导因子;

B——叶片数;

c——弦长;

φ——来流角;

r——截面位置;

CL,CD——翼型的升力和阻力系数.

来流角满足的关系为:

(3)

式中:Ω——风轮转速;

v——风速.

风轮产生的功率[10]为:

(4)

(5)

式中:ρ——空气密度;

R——风轮半径;

W——相对风速.

因此,风轮产生的功率主要取决于相对风速W,叶片数B,弦长c,来流角φ,风轮转速Ω,翼型的升阻力系数CL和CD,以及风轮半径R.

2　叶片优化设计数学模型

2.1风速频率的统计特性

风速分布一般均为正偏态分布,风力越大的地区,分布曲线越平缓,曲线的峰值降低并右移[11].这说明风力大的地区,大风速所占比例也多.通常用威布尔分布双参数曲线描述风速分布曲线,即:

(6)

其概率密度函数可表达为:

(7)

式中:k,z——威布尔分布的形状参数和尺度参数,根据经验分别取k=2,z=6.8 m/s.

2.2威布尔分布风速下优化设计数学模型

2.2.1目标函数

风力发电机组设计研制中,往往以发电价格的高低作为衡量其设计优劣的标准.为达到此目的,一方面可降低风力发电机组的制造成本和运行维护费用,另一方面要根据当地的风资源情况,尽可能使风力发电机组的运行工况与风资源匹配良好,以使风力发电机组获得最大的年发电量.本设计就以考虑威布尔分布的风速下的年发电量(Annual Energy Production,AEP)最大作为优化设计目标函数:

(8)

式中:P(vi)——风速为vi下的输出功率;

vi——风速;

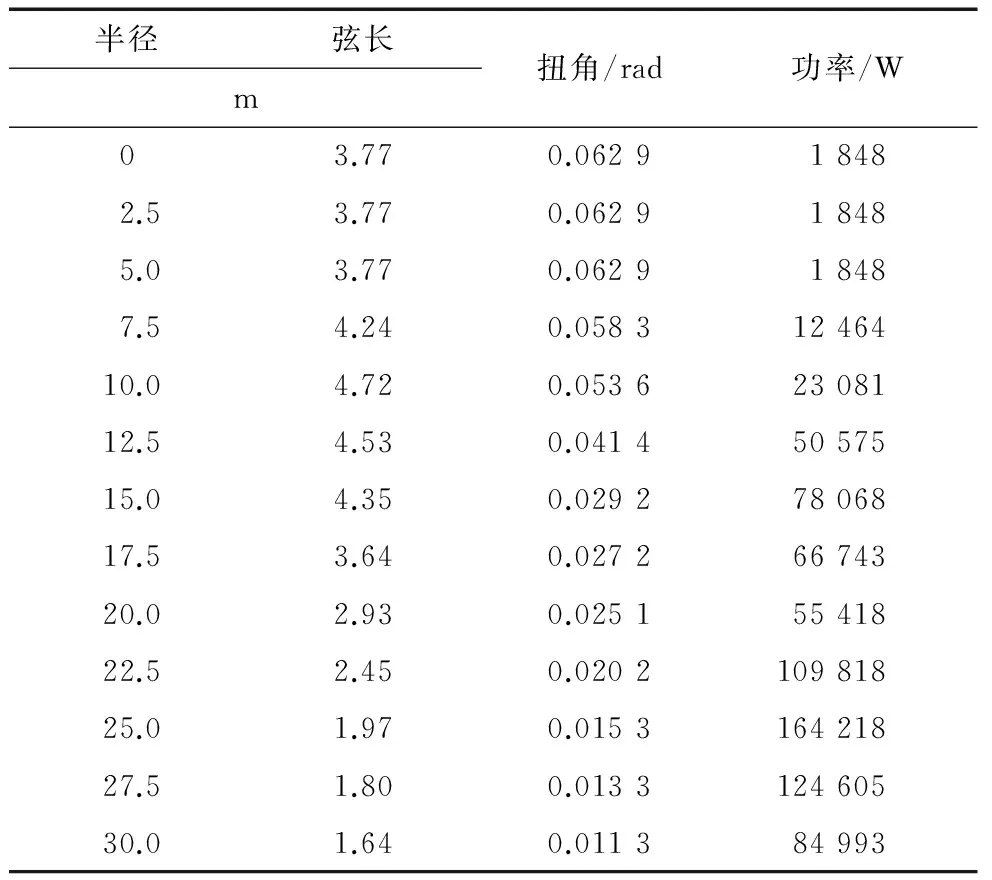
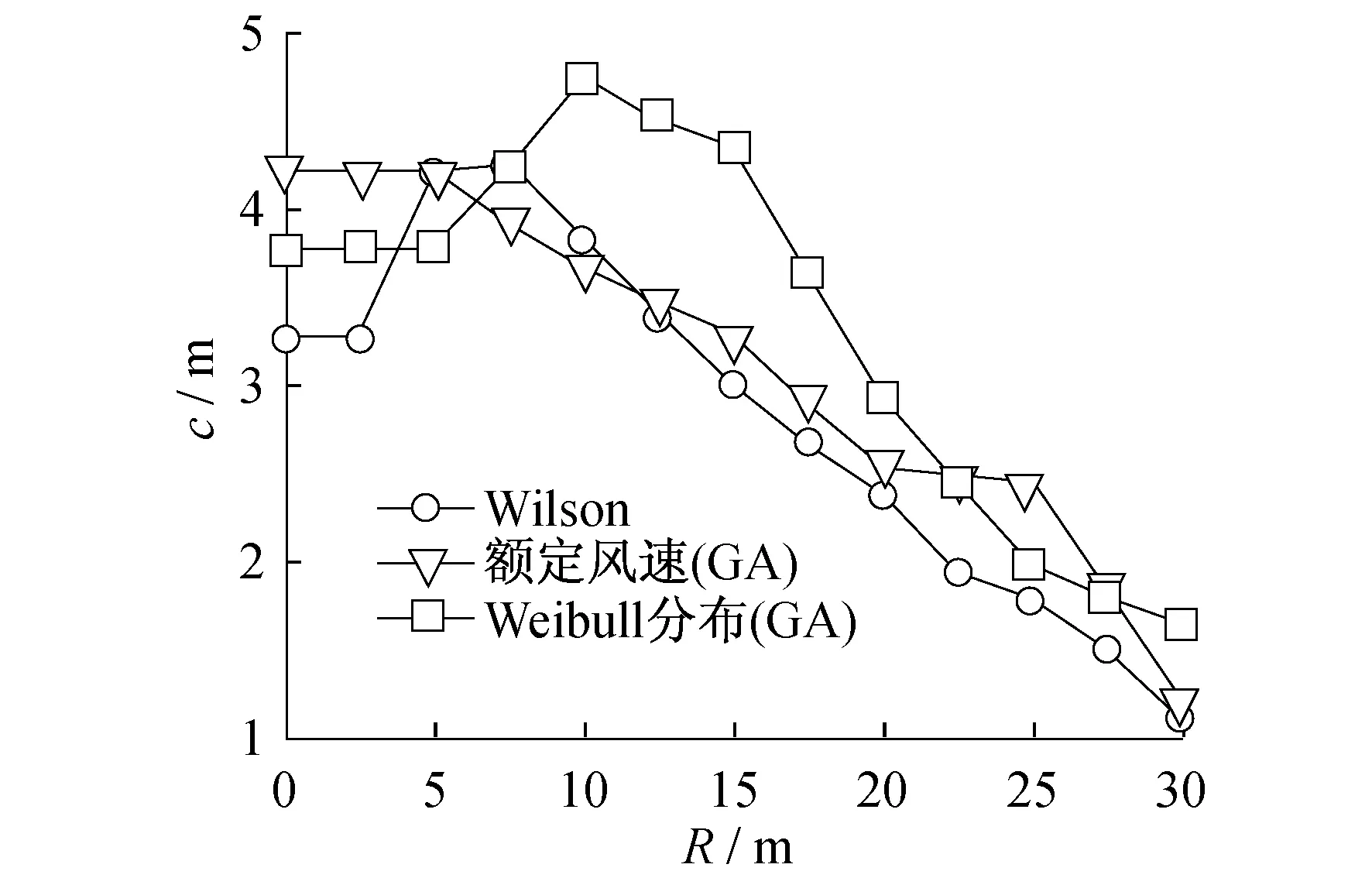
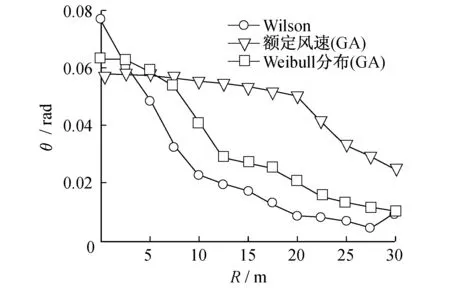
F(vi

2.2.2约束条件

风力发电机叶片优化设计的目的是获得较高的能量输出,其中的典型途径之一是对叶片几何外形进行优化,而弦长c和扭角θ是叶片外形的两个主要参数.在寻优的过程中,有时得出的结果虽然是最优的,但是有的参数往往会脱离实际情况.因此,需要对几何参数加以约束限制,即:

(9)

(10)

3　基于遗传算法的叶片优化设计

遗传算法是模仿自然界生物进化机制发展起来的随机全局搜索和优化方法,它借鉴了达尔文的进化论和孟德尔的遗传学说.其本质是一种高效、并行、全局搜索的方法,它能在搜索过程中自动获取和积累有关搜索空间的知识,并自适应地控制搜索过程以求得最优解.以弦长和扭角为设计变量、年发电量为目标函数及设计变量满足的要求作为约束条件,以每段产生的功率为适应度函数,利用Matlab软件编写程序,并调用遗传算法优化工具箱对1.5 MW风力机叶片气动外形进行优化设计.

3.1设计参数

风轮、风况及遗传算法基本参数见表1.

表1　风轮、风况及遗传算法基本参数

3.2优化结果

半径展向平分为13段,通过对每段多次优化寻优,得到的弦长和扭角分布如表2所示.

表2　弦长和扭角值

从表2的功率列可以看出,风力机叶片沿半径展向功率捕捉的主要部位集中在叶片的中部,这为更好地改善其气动性能提供了思路.

气动外形参数是风机叶片的关键参数,良好的外形不仅有利于气动性能的改善,而且还有利于叶片的加工和制造.图1和图2给出了3种情况(Wilson方法、额定风速及Weibull风速分布下用遗传算法)下叶片弦长和扭角的分布趋势.

图1　弦长分布

图2　扭角分布

从图1可以看出,3者得到的弦长整体趋势差别不大,但Wilson算法和额定风速下采用遗传算法所得到的弦长在靠近叶尖部分发生了一定的突变,故需要对计算结果进行一定的修正才能进行叶片的加工和制造;而Weibull风速分布下用遗传算法得到的弦长叶尖部分没有发生突变,整体呈现出流线型分布趋势,这样的变化趋势是有利于加工和制造的.

从图2可以看出,虽然Wilson方法得到的扭角在3者中整体上是最小的,但在叶尖部分出现了和弦长一样的突变问题;而额定风速下的遗传算法得到的扭角整体上又大于Weibull风速分布下用遗传算法得到的扭角,较小的叶片扭角有利于控制制造成本,因此综合考虑,Weibull风速分布下用遗传算法得到的扭角是较合理的.

4　结　语

本文采用遗传算法,在Weibull分布风速下对1.5 MW风力机进行了优化设计,优化后叶片气动外形参数弦长和扭角趋于流线型分布,克服了Wilson方法优化结果的局部最优及叶根部分突变的缺点,流线型的分布有利于叶片的加工和制造;此外,与额定风速下遗传算法的扭角相比,优化后的扭角呈减小趋势,节约了制造的成本,验证了该优化方法的可行性与合理性.

[1]蔡新,潘盼,朱杰,等.风力发电机叶片[M].北京:中国水利水电出版社,2014:175-176.

[2]WILSON R E,LISSAMAN P B S,WALKER S N.Aerodynamic performance of wind turbines[D].Corvallis:Oregon State University,1976.

[3]SPERA D A.Wind turbine techno logy[M].New York:ASM E Press,1994:53-58.

[4]杨涛,李伟,张丹丹.风力机叶片气动外形设计和三维实体建模研究[J].机械设计与制造,2010(7):190-191.

[5]傅洁,何斌,张慧玲,等.基于片条理论和遗传算法的风力机叶片全局优化设计[J].中南大学学报:自然科学版,2012,43(8):3 025-3 030.

[6]BENINI E,TOFFOLO A.Optimal design of horizontal-axis wind turbines using blade-element theory and evolutionary computation[J].ASME Journal of Solar Energy Engineering,2002(4):357-363.

[7]BURTON T,JENKINS N,SHARPE D,etal.Wind energy handbook[M].Wetsussex:John Wiley and Sons,2011:77-138.

[8]WILSON R E.Applied aerodynamics of wind power machines[D].Corvallis:Oregon State University,1974.

[9]MORGAN C A,GARRAD A D.The Design of optimum rotors for horizontal axis wind turbines[M].London:Garrad Hassanand Partners,1997:45-71.

[10]刘占芳,周振凯,邓智春.20 kW 定桨距风力机叶片优化设计[J].农业机械学报,2011,42(5):121-124.

[11]姚兴佳,田德.风力发电机组设计与制造[M].北京:机械工业出版社,2012:31-33.

(编辑胡小萍)

Optimization Design of Wind Turbine Blade Based on GeneticAlgorithm under the Weibull Distribution of Wind Speed

LI Shuaibin, WANG Hao, FAN Haizhe

(School of Energy and Mechanical Engineering, Shanghai University of Electric Power, Shanghai200090, China)

The model based on genetic algorithm is applied to optimize the aerodynamic performance of a 1.5 MW wind turbine blades,and the objective function is annual energy production under the wind speed of Weibull distribution.The wind turbine blade is divided into 13 segments along the spanwise,and the power of each segment is used as the fitness function of genetic algorithm.The optimized aerodynamic parameters are more reasonable than those of the Wilson method and Genetic algorithm under rated wind speed,and chord length and torsion angle present a more streamline distribution and the torsion angle decreases overall.

wind turbine blade; Weibull distribution; genetic algorithm; optimization design

10.3969/j.issn.1006-4729.2016.03.005

2015-03-23

简介：李帅斌(1989-),男,在读硕士,河南平顶山人.主要研究方向为风力发电机叶片的优化设计.E-mail:hnpj2009@163.com.

TK83

A

1006-4729(2016)03-0231-04