非光滑结构对轮胎抗水滑性能的影响

2016-07-25王国林薛开鑫

橡胶工业 2016年4期

王国林，薛开鑫，杨建

（江苏大学汽车与交通工程学院，江苏镇江 212013）

汽车在积水路面行驶时，一旦车速过高，会造成轮胎胎面接地区内积水不能及时经花纹沟排出，使轮胎与路面之间的附着性能急剧下降，极易导致汽车的滑行失控，严重威胁行车安全。因此，提高轮胎的抗水滑性能至关重要。国内外已经对轮胎抗水滑性能进行了大量研究，并取得显著成果。然而，轮胎性能间存在的矛盾使某一性能的提升以牺牲其他性能为代价。B.Wies等[1]研究表明，通过增大花纹沟体积提升1%的水滑速度，会增加约2.4%的噪声、降低0.6%的操控性能、增大0.4%的滚动阻力、降低0.3%的耐磨损和干地抓着性能。金梁[2]探索了非光滑花纹壁面对轮胎水滑速度的影响，结果表明，在不改变花纹沟体积的前提下，布置仿生凹坑形和V形非光滑壁面是提升轮胎水滑速度的有效途径之一。

非光滑结构源于科学家对自然界中具有减粘降阻的特殊生物体表结构的提取。20世纪70年代美国国家航空航天局（NASA）研究中心率先开展了鲨鱼皮表面结构的研究，发现鲨鱼体表分布着顺流向的微沟槽结构，减小了鲨鱼在水下高速游动时的阻力。封贝贝等[3]在飞行器表面加工沟槽结构，通过风洞试验得到了约18.4%的减阻率。S.R.Park等[4]用热线风速仪测量了沟槽内的流向速度场，通过对沟槽壁切应力的积分，得到了约4%的减阻率。徐继等[5]在旋成体表面布置不同深度和间距的三角形沟槽，得到了最大12.6%的减阻率。在管道运输方面，将多级泵的叶片表面设计成沟槽结构，输送效率提高了1.5%[6]。

本工作借鉴非光滑结构减阻特性的理念，通过在轮胎纵向花纹沟底部布置V形沟槽非光滑结构，在不改变花纹沟体积的前提下，减小雨水流过花纹沟的阻力，以提高轮胎的抗水滑性能。

1 V形沟槽非光滑结构模型的建立

1.1 花纹沟槽模型

以205/55R16半钢子午线轮胎为研究对象，其标准负荷为4 000 N，充气压力为0.24 MPa。为充分反映轮胎接地区特征，在进行轮胎水滑的计算流体力学分析前，利用Abaqus软件进行轮胎稳态滚动有限元分析，提取接地区变形后的胎面形状，以接地变形后的纵向花纹沟作为分析对象，如图1所示。一般而言，轮胎纵向花纹沟起主要排水作用，为探索非光滑花纹沟底对轮胎水滑速度的影响，以文献[2]的轮胎有限元分析为基础，在纵向花纹沟底布置V形沟槽非光滑结构，分析其分布对轮胎抗水滑性能的影响。

图1 花纹沟槽模型的建立

1.2 V形沟槽数学模型的建立

由于整体模型水滑分析计算时间较长，为了提高效率以及方便正交试验分析，提取单个纵向花纹沟的子模型进行分析，如图2所示。在三维欧式空间XYZ中，V形沟槽相当于沿着轮胎周向分布的肋条，则V形沟槽非光滑沟底表面的数学模型如下：

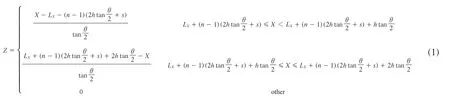
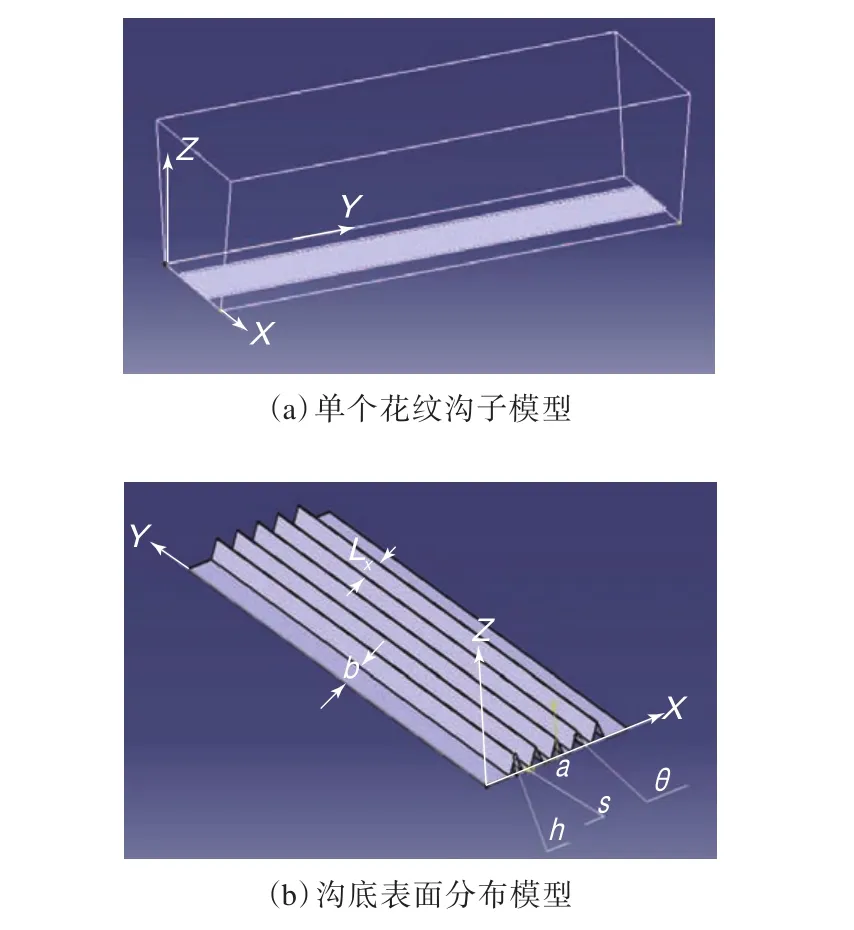
图2 V形沟槽子模型

模型中沟槽为对称的V形结构，且整体呈对称分布，n为沿着X正向沟槽的序号，n=1，2，3，…，m，m为沟槽的条数。

由流体边界层理论可知[7]，边界层厚度（δ）计算公式为

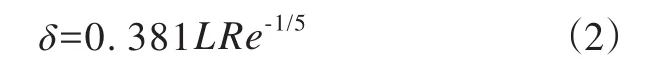
其中，L为特征长度，Re为雷诺数。根据轮胎接地长度可以得到花纹沟的最大边界层厚度约为0.96 mm，所选择的非光滑结构尺寸必须在此范围内。根据实际花纹沟尺寸，a=7.5 mm，且满足下式：

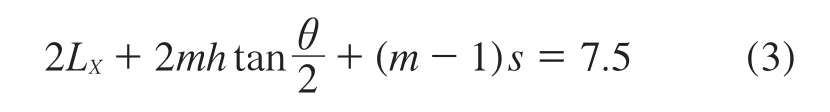
进而推出下式：

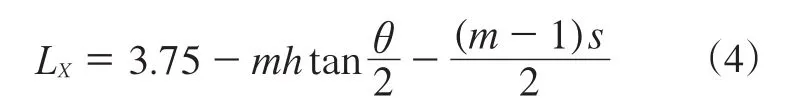
不同的参数取值确定不同的LX，从而确立了花纹沟底V形沟槽的具体布置。

1.3 控制方程及湍流模型

对于湍流模拟分析，目前主要有直接数值模拟（DNS）、大涡数值模拟（LES）和雷诺平均数值模拟（RANS）3种控制方程。其中，RANS能够真实地反映边界层内部主要漩涡分布等微观流场信息，且计算量小，效率高，其连续方程和雷诺平均Navier-Stokes方程分别见式（5）和（6）[8]：

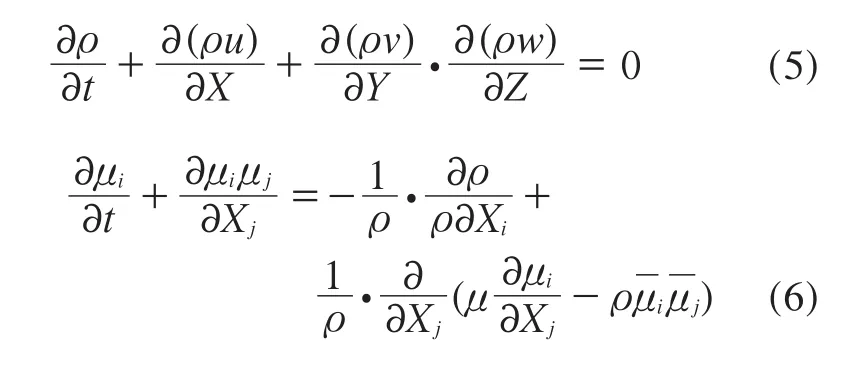
式中，ρ为水的密度，t为时间，u，v，w分别为X，Y，Z方向上的速度分量，μ为流体粘度，μi和μj为时均速度。

湍流模型选用SSTk-ω模型，它集中了高雷诺数k-ε模型以及低雷诺数k-ω模型的优点，利用混合函数实现从边界层内部的标准k-ω模型到边界层外部的高雷诺数的k-ε模型的逐渐转变，使近壁面到充分发展区域的过渡更加完美，计算的精度更高，参数k和ω的方程见式（7）和（8）[9]：

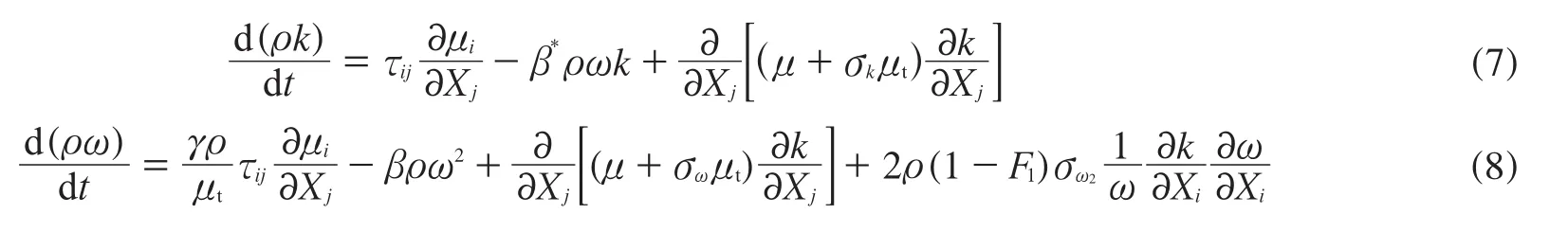
式中，β*和β为模型常数，μt为湍动粘度，σk和σω分别为与湍动能和耗散率对应的普朗特常数，γ为热导率，τij为湍流剪切应力，F1为开关函数，σω2为模型常数。

1.4 计算域网格划分

将图2所示的花纹沟槽计算域导入Hypermesh中进行网格划分，采用结构网格与非结构网格相结合的方法，为扑捉近壁区水流运动特征，靠近壁面的区域进行网格细化。边界层的粘性底层约为0≤y+≤5（y+为壁面无量纲距离），因此靠近壁面的第1个网格的无量纲数必须控制在y+≤5内，而贴近壁面的第1层网格厚度（y）可由下式求出：

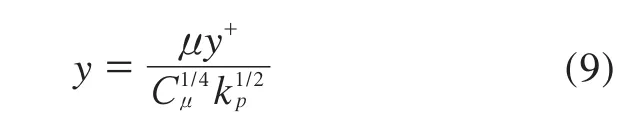
其中，Cμ为经验常数，取0.09；kp为第1个节点的湍动能[10]。此外，对于SSTk-ω模型，边界层内网格数至少为15个。经过反复尝试，最终将第1层网格的尺寸取0.01 m，增长率为1.2，计算域最大网格尺寸为0.2 mm，网格划分如图3所示。

图3 单个花纹沟网格模型

2 正交试验分析

选用L16（45）正交表，在25 m s-1水流速度下，以h（mm），θ（°），s（mm），m（条）为仿真试验因子，分别记为A，B，C，D，因子水平见表1，正交试验方案及计算结果见表2。

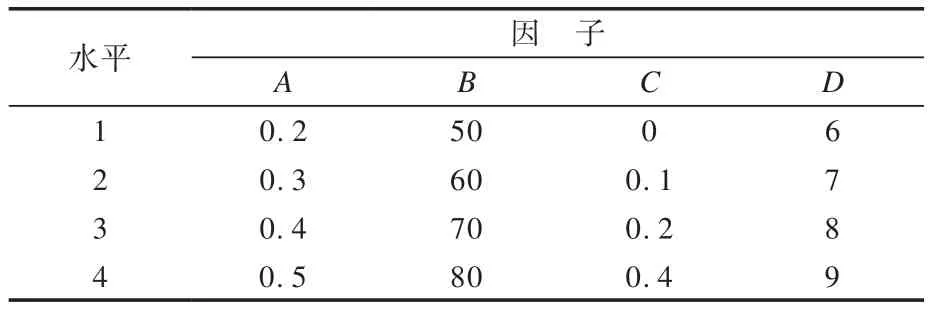
表1 因子水平表

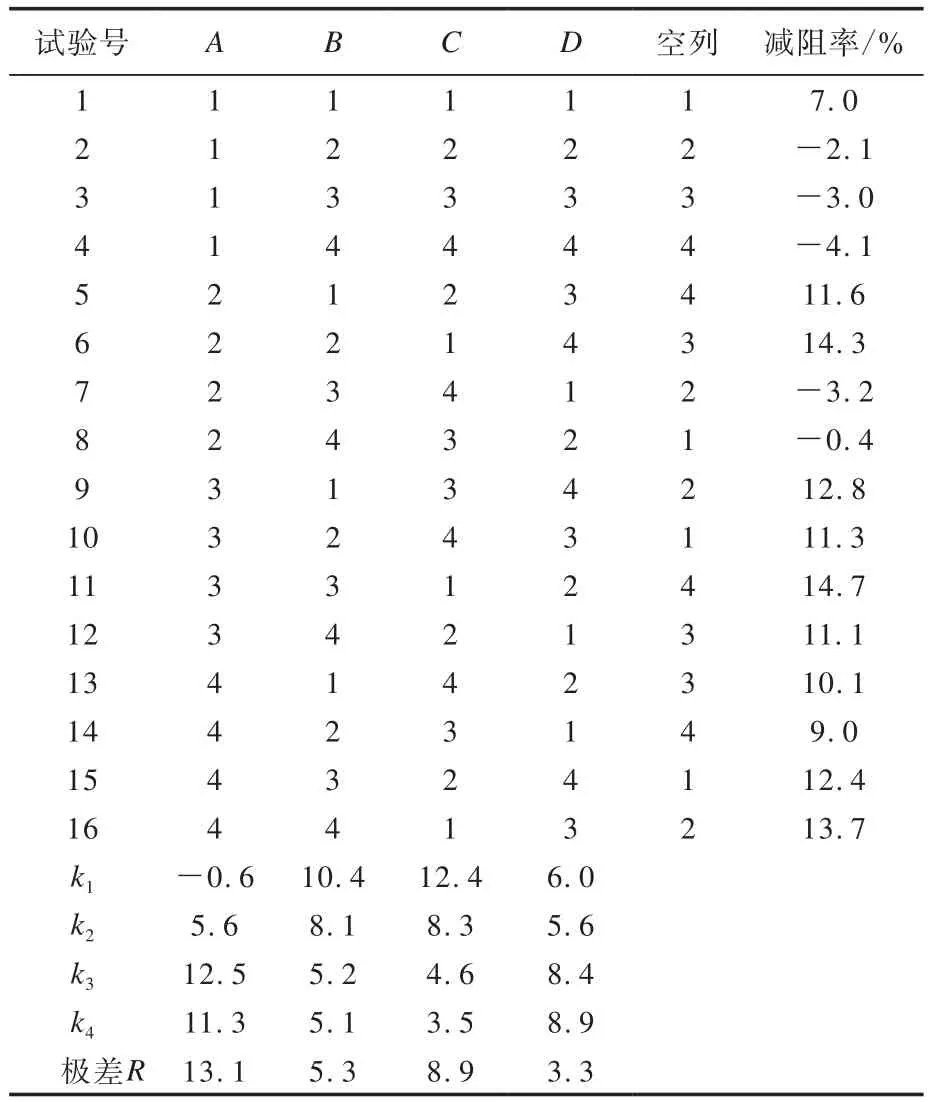
表2 正交试验方案及计算结果

3 结果分析

为便于分析V形沟槽非光滑结构的减阻效果，定义减阻率（Q）如下：

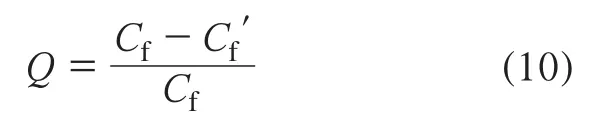
式中，Cf为光滑的原始模型的壁面阻力系数，Cf′为V形沟槽非光滑表面的壁面阻力系数。Q为正表明减阻，Q为负表明增阻。Cf计算公式为

其中，F为壁面阻力，T为垂直于来流方向的投影面积。Cf′计算参照Cf。仿真试验分析结果表明，h对减阻效果影响最大，然后依次是θ，s，m。在试验因子范围内的减阻效果最佳组合为A3B1C1D4，即h为0.4 mm，θ为50°，s为0，m为9条。

3.1 壁面剪切应力分析

光滑表面和布置V形沟槽表面的剪切应力对比如图4所示。由图4可以看出，二者的剪切应力在进口处相等，但是沿流向方向移动时，V形沟槽壁面剪切应力明显小于光滑壁面，尤其在布置沟槽的区域，壁面剪切应力明显减小。

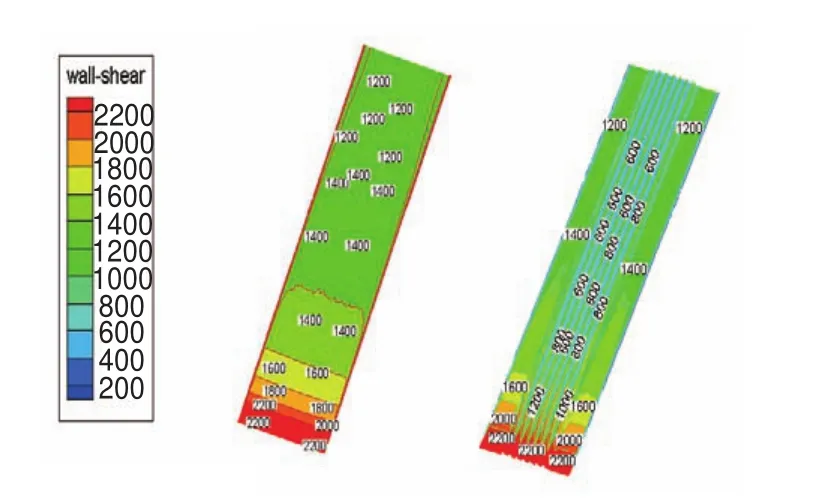
图4 光滑与非光滑模型壁面剪切应力对比

光滑表面和V形沟槽表面垂直于流向的某个特征平面的剪切应力对比如图5所示。由图5可见：光滑壁面剪切应力保持2 kPa不变，距光滑壁面越远剪切应力越小；对于V形沟槽壁面，剪切应力在沟槽尖顶附近最大，越接近沟槽谷底越小，V形沟槽改变了壁面的应力分布，将光滑壁面均匀分布的大应力转变为沟槽仿生壁面尖顶很小区域的大应力、绝大部分区域小应力的阶梯递减式分布。因此，V形沟槽壁面减小了壁面的平均剪切应力和水流通过花纹沟的阻力。

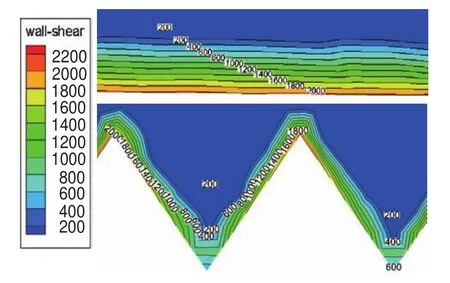
图5 特征平面剪切应力对比

3.2 速度场分析

光滑壁面和V形沟槽壁面在某个特征平面上流向速度对比如图6所示。从图6可以看出，V形沟槽壁面流场与光滑壁面流场有明显不同，光滑壁面的附面层内速度在很短距离内就达到了主流速度，意味着其边界层很薄，光滑壁面在该处的速度变化较V形仿生壁面更加剧烈，而V形沟槽壁面达到主流速度的距离较大。这是因为V形沟槽结构内部存在低速流体，使得表面附面层内的速度降低，同时也降低了速度梯度分布，这相当于增大了粘性底层边界层厚度，使表面摩擦阻力降低。

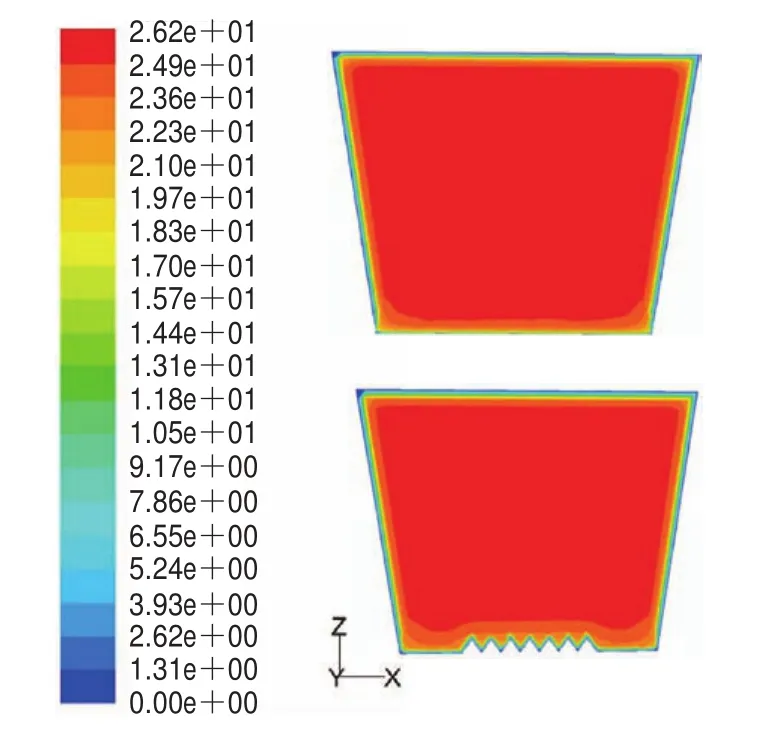
图6 光滑与非光滑模型特征平面流向速度对比

4 轮胎水滑分析

将正交试验优选出的方案布置于轮胎花纹沟槽底部，进行轮胎水滑分析，并与原始光滑结构进行对比。考虑模型的对称性，采用接地区一半区域进行分析。V形沟槽非光滑结构的半胎水滑分析模型网格如图7所示，模型中采用结构网格和非结构网格相结合的方法进行网格划分，采用湍流模型分析，边界条件等设置同单个花纹沟分析。结果表明，V形沟槽结构的胎面动水压力相比于原始模型有所降低，原始模型和非光滑结构模型的胎面动水压力分别为131.536和127.816 kPa。根据动水压力计算公式P=1/2ρv2，可以推算出V形沟槽非光滑沟底花纹沟可以使轮胎水滑速度提升1.2 km h-1。