基于重要度的改进型装备可靠性鉴定试验优化方法

兑红炎, 陈立伟, 陈刚

(1.郑州大学, 河南 郑州　450001; 2.中国兵器试验中心, 陕西 华阴　714200)



基于重要度的改进型装备可靠性鉴定试验优化方法

兑红炎1, 陈立伟1, 陈刚2

(1.郑州大学, 河南 郑州450001; 2.中国兵器试验中心, 陕西 华阴714200)

摘要：在对重要度理论和装备可靠性鉴定试验方法研究的基础上，重点探讨了重要度计算方法对装备可靠性鉴定试验优化的作用机理，提出了一种基于重要度理论的改进型装备可靠性鉴定试验优化方法；结合坦克可靠性鉴定试验过程，给出了重要度理论在改进型装备被试品和参试品确定、试验应力选择中的具体应用方法，并通过对改进型装备可靠性鉴定试验优化效果分析，讨论了该方法的有效性和先进性。

关键词：成本降低;试验设计;重要度;可靠性分析

可靠性鉴定试验[1]作为对装备可靠性评估的有效手段，是目前装备定型审查的规定做法，也是大型复杂装备定型试验的必需考核项目。我国于1990年制定了《可靠性鉴定和验收试验》军用标准[2]，并于2009年进行了修订，已经成为指导我国国防科研领域的重要标准之一，具有法律约束力。颜世刚等[3]详细论述了舰炮火控系统可靠性鉴定试验原理。王春晖等[4]研究一种可靠性鉴定试验中受试样品的软硬件联合测试方法。袁志勇等[5]制定了自导与引信系统的可靠性鉴定试验方案。

重要度[6]是指系统中单个或多个组(部)件失效或状态改变时其对系统性能的影响程度，它是组(部)件可靠性参数和系统结构的函数。在系统设计阶段，重要度用来帮助设计人员识别系统薄弱环节，为整个系统可靠性提升和优化设计提供支撑依据；在系统运行阶段，重要度用于合理分配资源到关键的组(部)件，从而最大化整个系统正常运行的时间；在系统维修阶段，重要度用来帮助维修人员以最小的成本来提高系统性能，从而延长系统寿命或提高系统性能。

1969年，Birnbaum[6]首先提出了可靠性重要度分析方法的概念，表示在已知组(部)件可靠性的情形下，组(部)件可靠性的变化对系统可靠性的影响程度。在Birnbaum 提出系统重要度分析方法的基础上，关键重要度、F-V重要度、B-P重要度、冗余重要度、组合重要度等相继提出[7]，它们在不同结构，不同状态条件下，从不同层面分析了组(部)件的变化对系统性能的影响程度，丰富了重要度理论。在国内，北京理工大学的崔利荣研究团队[8]、西北工业大学的司书宾研究团队[9-11]、中国科学院的王海涛研究团队[12]、东北大学的田宏研究团队[13]、大连交通大学的毕卫星研究团队[14]等对重要度分析方法进行了扩展，取得了良好的研究成果，为重要分析方法的应用奠定了理论基础。

改进型装备是在原有装备的基础上进行改进而来，其结构与上一代装备有相同之处。可靠性鉴定试验通常需要付出高昂的试验成本(包括装备样品的寿命耗尽、试验环境的模拟、油料、电力、弹药及人工成本等等)。如果对改进型装备与上一代装备相同的组(部)件进行重复可靠性试验，势必造成资源浪费，降低可靠性鉴定试验的效率。本文利用重要度理论，识别改进型装备的薄弱环节，得出组(部)进行可靠性鉴定试验的排序，对可靠性鉴定试验设计进行优化，从而节约装备研制成本和缩短研制周期。

1可靠性重要度

1.1假设条件

1)系统和组(部)件具有故障和工作2个状态，其中状态0表示故障，状态1表示工作。

2)组(部)件之间相互独立。

1.2符号说明

n为系统中的组(部)件数量

Xi(t)为t时刻组(部)件i的状态

Φ(X(t))为t时刻系统的结构函数,Φ(X(t))=Φ(X1(t),X2(t),…,Xn(t))

Pi1(t)为t时刻组(部)件i的可靠性,Pi1(t)=Pr{Xi(t)=1}

R(t)为t时刻系统可靠性,R(t)=Pr{Φ(X(t))=1}

Ii(t)为t时刻组(部)件i的可靠性重要度

1.3可靠性重要度

可靠性重要度[6]描述了一个组(部)件可靠性变化对于系统可靠性变化的影响,如(1)式所示。从系统状态概率分布和结构函数的角度分析,(1)式还可进一步变换为(2)式,其物理意义是指组(部)件i从工作状态变为失效状态时,系统可靠性的变化值。

(1)

(2)

2改进型装备可靠性鉴定试验优化

改进型装备可靠性鉴定试验优化的基本思路是:将装备结构和应力施加作为可靠性试验中可以进行优化的2个方面为出发点,将各自看做一个独立的系统,通过重要度的方法分别进行优化,从而达到对可靠性鉴定试验进行优化的目的,以提高试验效率,降低试验成本。具体研究步骤如下:

1) 以串联和并联作为系统的演化推进方式,研究系统重要度的漂移规律,找出系统薄弱环节,确定被试品中需重点考核和适应性考核的组(部)件;

2) 以第一步确定的被试品考核组(部)件为对象,研究不同应力组合对组(部)件的影响,基于重要度对应力进行取舍,实现可靠性鉴定试验的优化。

2.1基于重要度的改进型装备结构演化规律

改进型装备的结构发展经历了从简单到复杂,再到简单的过程,在复杂装备的高可靠性要求下,复杂装备的结构被要求越简单越好。装备从以前的复杂的拓扑结构发展为简单的串联和并联结构,降低了组(部)件之间的相互关联性,提高了其独立性。本节主要以串联和并联作为系统的演化推进方式。

2.1.1串联结构

在图1中,系统演化过程为单个的组(部)件1串联组(部)件2形成结构1,继续串联组(部)件3形成结构2,继续串联n-3个组(部)件,形成n个组部件串联的结构3。

图1　串联结构演化图

在结构0中,由于只有1个组部件,因此系统的结构函数为Φ(X(t))=min{X1(t)}。系统的可靠性函数为R(t)=P11(t)。各组(部)件重要度为 I1(t)=1。

在结构1中,系统的结构函数为Φ(X(t))=min{X1(t),X2(t)}。系统的可靠性函数为R(t)=P11(t)P21(t)。各组(部)件重要度为 I1(t)=P21(t),I2(t)=P11(t),所以如果P21(t)≥P11(t),那么I1(t)≥I2(t)。

同理,在结构2中,如果P31(t)≥P21(t)≥P11(t),那么I1(t)≥I2(t)≥I3(t)。由此可推得在n组(部)件串联系统中,可靠性越小的组(部)件,其相对系统来说重要度越高。

性质1在串联结构演化系统中,如果新增加的组(部)件可靠性最小,那么在可靠性鉴定试验中,该组(部)件应作为被试品。

假设在串联结构演化系统中,组(部)件n是新增加的组(部)件,如果Pn1(t)≤…≤P21(t)≤P11(t),那么I1(t)≤I2(t)≤…≤In(t)。所以在串联结构演化系统中,可靠性越小的组(部)件,其对系统可靠性的影响就越大,那么在可靠性鉴定试验中,该新增加的组(部)件应作为被试品。

由此可见,在相互独立的串联系统中,当增加一个串联组(部)件形成下一代装备时,其薄弱环节取决于新系统的所有组(部)件各自的可靠性,而不仅仅是新增加的组(部)件,可靠性越低的组(部)件,对系统可靠性的影响就越大。因此从系统设计的角度来讲,为了提高系统可靠性应该对可靠性低的组(部)件采取措施,使其可靠性提高。对于鉴定试验来讲,应该重点关注可靠性低的组(部)件,并进行针对性的应力设计,从而能快速发现系统的薄弱环节或通过鉴定。

2.1.2并联结构

在图2中,系统演化过程为单个的组(部)件1并联组(部)件2形成结构1,继续并联组(部)件3形成结构2,继续串联n-3个组(部)件,形成n个组部件并联的结构3。

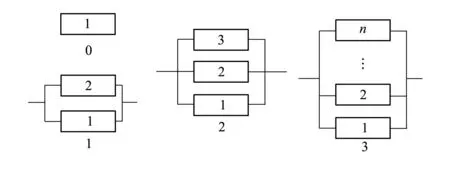
图2　并联结构演化图

在结构0中, I1(t)=1。

在结构1中,系统的结构函数为Φ(X(t))=max{X1(t),X2(t)}。系统的可靠性函数为R(t)=P11(t)+P21(t)-P11(t)P21(t)。各组(部)件重要度为 I1(t)=1-P21(t),I2(t)=1-P11(t),所以如果P21(t)≥P11(t),那么I1(t)≤I2(t)。

同理,在结构2中,如果P31(t)≥P21(t)≥P11(t),那么I1(t)≤I2(t)≤I3(t)。由此可推得在n组(部)件的并联系统中,可靠性越大的组(部)件,其相对系统来说重要度越高。

性质2在并联结构演化系统中,如果新增加的组(部)件可靠性最大,那么在可靠性鉴定试验中,该组(部)件应作为被试品。

假设在并联结构演化系统中,组(部)件n是新增加的组(部)件,如果Pn1(t)≥…≥P21(t)≥P11(t),那么I1(t)≤I2(t)≤…≤In(t)。所以在并联结构演化系统中,可靠性越大的组(部)件,其对系统可靠性的影响就越大,那么在可靠性鉴定试验中,该新增加的组(部)件应作为被试品。

由此可见,在相互独立的并联系统中,当增加一个并联组(部)件形成下一代装备时,其薄弱环节取决于新系统的所有组(部)件各自的可靠性,而不仅仅是新增加的组(部)件,可靠性越高的组(部)件,对系统可靠性的影响就越大。对于鉴定试验来讲,应该重点关注可靠性高的组(部)件,如果为了发现系统缺陷可以逐步隔离可靠性高的组(部)件,并进行针对性的应力设计,从而能快速发现使系统性能降低的关键环节或通过鉴定。

2.2基于应力的装备可靠性鉴定试验优化

根据GJB150-86《军用设备环境试验方法》试验应力主要有低气压、高温、低温、温度冲击、湿热、太阳辐射、振动、冲击、电应力等。在可靠性鉴定试验中,应力的来源主要是根据装备在实际使用过程中所面临的应力环境而制定的。

构建应力施加模型时,各种应力对装备的影响是相互独立的。因为在可靠性鉴定试验中,任何一种应力造成装备出现致命故障,则该可靠性鉴定试验就不能通过,即装备必须在所有可能的应力环境中稳定工作。因此在应力的施加模型中,可以认为应力施加过程是一个串联系统,如图3所示。

图3　应力施加结构模型

根据上述的应力重要度计算,针对被试品对不同应力敏感度的不同,将其通过该应力的概率作为重要度计算的基础数据,基于重要度对应力进行排序。在不同的应力环境下,各单元对可靠性试验中的不同应力敏感度是不一样,即有些应力可以使某个单元以较大概率失效,有些应力对某些单元没有任何影响,不会影响可靠性试验的结果。因此在可靠性试验的应力设计时可以进行取舍,从而实现可靠性鉴定试验的优化。

3案例分析

本节以坦克电子综合化系统为例对上述优化方法进行验证,以确定其正确性。坦克电子综合化系统[15]可靠性框图如图4所示。

图4　坦克电子综合化系统可靠性框图

在整个电子综合化系统中,电源控制分配为整个电子系统供电;在整个作战流程中,由战场指挥系统对坦克进行任务下达,由观瞄跟踪系统发现目标,由火控计算机、综合导航定位系统提供的坐标信息和车体姿态信息进行实时计算,将计算结果发送与炮控系统进行火力线对准,由炮长通过车际通信系统指挥其他人员(如车长、装填手等)进行射击准备,最后完成射击。车长监控系统用于实时监控坦克各种状态信息;综合防护系统用于防护导弹、核生化等袭击。车长监控系统和综合防护系统提高了整个坦克完成任务的概率,不介入主要作战流程,在分析时应单独考虑,这里用虚线表示其与主要作战组(部)件的关系。

根据图4可靠性框图可以得到系统的结构函数为

(3)

则系统可靠性为

(4)

基于(1)式,各组(部)件的重要度分别为

P21(t)P31(t))P41(t)·P51(t)·P61(t)·P71(t);

P51(t)·P61(t)·P71(t);

P51(t)·P61(t)·P71(t);

P21(t)P31(t))·P11(t)·P51(t)·P61(t)·P71(t);

P21(t)P31(t))·P11(t)·P41(t)·P61(t)·P71(t);

P21(t)P31(t))·P11(t)·P41(t)·P51(t)·P71(t);

P21(t)P31(t))·P11(t)·P41(t)·P51(t)·P61(t)

在前述坦克综合化系统中可假设战场指挥系统和导航定位系统为新研单元,其可靠性根据研制阶段所得数据为0.9,即:P21(t)=0.9,P51(t)=0.9;其他单元据资料计算所得的可靠性分别为:P11(t)=0.98;P31(t)=0.98;P41(t)=0.98;P61(t)=0.98;P71(t)=0.98;P81(t)=0.98;P91(t)=0.98;代入重要度表达式计算得各单元重要度排序如表1所示。

表1　坦克电子综合化系统组(部)件重要度排序

由表1可知,对于坦克电子综合化系统来说,对系统可靠性影响最大的可更换单元为导航定位系统,其次为电源控制分配、火控计算机、炮控系统及车际通信系统,然后是观瞄跟踪系统,最后是战场指挥系统。因此在可靠性鉴定试验中应该把新研的导航定位系统作为重点,因为它对整个系统的可靠性影响最大,也是最重要的单元。电源控制分配等排序第二的作为一般单元,观瞄系统排序靠后且为已定型产品,可作为参试品,在可靠性试验应力设计时可不再单独考虑。战场指挥系统虽然是新研产品,但从整个作战角度来讲并不是最重要的,因为观瞄系统可以部分取代其功能,在其失效的情况下,整个坦克电子综合化系统仍然可以完成基本战斗任务(降级使用),但作为新研单元,在可靠性鉴定试验中还是应进行相应的应力安排,但整个系统因为战场指挥系统的原因而出现系统致命故障的概率很低,对整个可靠性鉴定试验的结论影响仍然十分有限。基于图3,针对坦克电子综合化系统,在冲击、振动应力条件下,光纤陀螺导航定位系统比机械陀螺导航定位系统通过可靠性鉴定试验的概率大。以现在流行的光纤陀螺导航定位系统为例,其对太阳辐射不敏感,可以赋予P51(t)极高概率值,抗冲击、振动应力效果良好,可以赋予P71(t)、P61(t)较高概率值,对高温、低温、温度冲击敏感度一般,可以赋予P11(t)、P21(t)、P31(t)一般概率值,对湿热、电应力和低气压较为敏感可以赋予P41(t)、P81(t)、P91(t)较低概率值,由此,可以得到一个在不同应力条件下通过概率的排序,代入各应力计算公式可得到各种应力的重要度排序

(5)

其中约等号表示重要度数值接近,但不完全相等。

根据各种应力的重要度排序,在实际试验应力的设计中就可以将太阳辐射、冲击、振动等应力舍去,高温、低温和温度冲击做一般适应性考核,对电应力、湿热和低气压做严格考核。

根据以上的分析,基于表1和公式(5),优化后的重点被试品为导航定位系统;独立考核为综合防护系统、车长监控系统;一般被试品为电源控制分配、炮控系统、火控计算机、车际通信系统、战场指挥系统。优化后的重点应力为电应力、湿热、低气压;一般应力为高温、低温、温度冲击。所以优化前被试品为9个,优化后重点被试品1个,一般被试品5个,独立考核2个。优化前应力为9种,优化后为重点应力3种,一般应力3种。

由此可见,在对被试品进行优化后,再在前者的基础上进行试验应力的设计及优化会使整个试验的对象和应力施加种类大为减少,而做了此类优化后,对试验结果的影响概率极低。对于改进型装备来说,在定型试验时进行此类优化的风险也是极低的,节约了时间,降低了成本。

4结论

本文利用可靠性重要度对被试品进行了优化，得到了改进型装备在可靠性鉴定试验中被试品各单元对系统通过试验的影响程度排序，以此为基础对被试对象进行了等级划分，在试验方案的设计中实现有针对性的考核。在此基础上，利用被试对象对试验应力的敏感程度得到在各种应力条件下被试品出现故障的概率，采用重要度的方法，对试验应力进了重要程度划分，并以此为依据在试验设计时对应力进行取舍，从而实现了整个改进型装备在可靠性鉴定试验中的优化。

参考文献：

[1]Awad M. Economic Allocation of Reliability Growth Testing Using Weibull Distributions[J]. Reliability Engineering and System Safety, 2016, 152: 273-280

[2]杨喜存，单军勇. 从某正样机的鉴定试验谈可靠性试验设计[J]. 装备环境工程，2015，12(1): 93-96

Yang Xicun, Shan Junyong. Reliability Test Desigh Based on Reliability Qualification Test of a Main Sample Machine[J]. Equipment Environment Engineering, 2015, 12(1): 93-96 (in Chinese)

[3]颜世刚, 刘向明, 李峻年. 定时截尾的舰炮火控系统可靠性鉴定试验方法[J]. 火力与指挥控制, 2014, 39: 172-175

Yan Shigang, Liu Xiangming, Li Junnian. Reliability Test for Qualification Method of Shipborne Gun Fire Control System Based on Type-I[J]. Fire Control & Command Control, 2014, 39: 172-175 (in Chinese)

[4]王春晖, 邱述斌. 可靠性鉴定试验受试样品的软硬件联合测试技术[J]. 装备环境工程, 2014, 11: 64-68

Wang Chunhui, Qiu Shubin. Study on Hardware-Software Join Test Technology for Reliability Qualification Test[J]. Equipment Environmental Engineering, 2014, 11: 64-68 (in Chinese)

[5]袁志勇, 陈宜辉. 自导深弹中自导与引信系统的Bayes可靠性鉴定试验方案[J]. 弹箭与制导学报, 2015(2): 73-75

Yuan Zhiyong, Chen Yihui. A Bayesian Plan of Reliability Verification Test about Homing and Fuse System of Homing Depth Charge[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2015(2): 73-75 (in Chinese)

[6]Birnbaum Z W. On the Importance of Different Components in a Multi-Component System[M]. New York, Academic Press, 1969, 581-592

[7]Kuo W, Zhu X. Importance Measures in Reliability, Risk, and Optimization: Principles and Applications[M]. New York, John Wiley & Sons, 2012

[8]Cui L. The IFR Property for Consecutive-k-out-of-n: F Systems[J]. Statistics & Probability Letters, 2002, 59(4): 405-414

[9]Si S, Dui H, Zhao X, et al. Integrated Importance Measure of Component States Based on Loss of System Performance[J]. IEEE Trans on Reliability, 2012, 61(1): 192-202

[10] Dui H, Si S, Cui L, et al. Component Importance for Multi-State System Lifetimes with Renewal Functions[J]. IEEE Trans on Reliability, 2014, 63(1): 105-117

[11] Dui H, Si S, Zuo M, et al. Semi-Markov Process-Based Integrated Importance Measure for Multi-State Systems[J]. IEEE Trans on Reliability, 2015, 64(2): 754-765

[12] 王海涛, 吴宜灿, 李亚洲,等. 核电站实时风险管理系统部件重要度计算方法研究[J]. 核科学与工程, 2008, 28(1): 61-65

Wang Haitao, Wu Yican, Li Yazhou, et al. Study on the Algorithm of the Calculation of the Components′ Importance Measures in A Risk Monitor[J]. Journal of Nuclear Science and Engineering, 2008, 28(1): 61-65 (in Chinese)

[13] 田宏, 陈宝智, 吴穹,等. 多态系统可靠性及元素的不确定性重要度[J]. 东北大学学报, 2000, 21(6): 634-636

Tian Hong, Chen Baozhi, Wu Qiong, et al. Multistate System Reliability and Uncertainty Importance of Its Components[J]. Journal of Northeastern University, 2000, 21(6): 634-636 (in Chinese)

[14] 毕卫星, 陈建军. 一种改良的联合重要度算法[J]. 大连交通大学学报, 2009, 30(5): 74-76

Bi Weixing, Chen Jianjun. An Improved Algorithm on Joint Failure Importance[J]. Journal of Dalian Jiaotong University, 2009, 30(5): 74-76 (in Chinese)

[15] 周启煌, 常庆天, 邱晓波. 战车火控系统与指控系统[M]. 北京:国防工业出版社, 2003

Zhou Qihuang, Chang Qingtian, Qiu Xiaobo. Fire Control System, Command and Control System of Combat Vehicle[M]. Beijing, National Defense Industry Press, 2003 (in Chinese)

Optimization Method of Improved Equipment Reliability Analysis Test based on Importance Measure

Dui Hongyan1, Chen Liwei1, Chen Gang2

1.Zhengzhou University, Zhengzhou 450001, China;2.China Ordnance Test Center, Huayin 714200, China

Abstract:The introduction of the full paper reviews a number of papers in the open literature and then proposes the representation method in the title, which is explained in sections 1 and 2. Section 1 briefs the system assumptions and the equation of reliability importance measure. The core of section 2 consists of: (1) we build the reliability model of the tank integrated system, which is given by Fig. 2; (2) we analyze the component reliability in the tank integrated system, give the computation of component importance, and discuss the order of different component importance as in Table 1; (3) we get the scheme of the reliability test by determining the test object based on the component importance. Section 3 presents the optimal scheme of the reliability test based on the stresses sensibility. Results comparisons, presented in Table 2, and its analysis verify that the importance measure can determine the test objects and stresses, so as to crop military and the test cost.

Keywords:cost reduction, design of experiment, importance measure, reliability analysis

收稿日期：2016-03-22基金项目：国家自然科学基金(71501173, 61401403)、河南省基础与前沿研究基金(142300410359)与郑州大学青年教师启动基金(1511326001)资助

作者简介：兑红炎(1982—)，郑州大学管理工程学院讲师，主要从事可靠性和重要度的研究。

中图分类号：N945.17

文献标志码：A

文章编号:1000-2758(2016)04-0571-07