冲击作用下液滴在环境液体中的变形破碎行为

廖斌，张桂夫，王鲁海，朱雨建，*，杨基明

(1．中国科学技术大学近代力学系，合肥230027;2．安徽工程大学建筑工程学院，安徽芜湖241000)

冲击作用下液滴在环境液体中的变形破碎行为

廖斌1，2，张桂夫1，王鲁海1，朱雨建1，*，杨基明1

(1．中国科学技术大学近代力学系，合肥230027;2．安徽工程大学建筑工程学院，安徽芜湖241000)

采用基于液-液体系的坠落实验装置对冲击作用下单个液滴在环境液体中的变形破碎行为进行了实验研究。针对高速摄影捕捉到的5种液滴典型变形破碎模式进行了定量化考察和规律性分析。结果表明，液滴初始直径、液滴与环境液体的密度比和粘度比、界面张力系数以及坠落高度等实验参数相互组合可以得到相似的实验结果，其中We数是区分液滴变形破碎模式的关键参数。进一步研究液滴变形破碎模式与无量纲参数的依赖关系发现，在1＜We＜700、0．001＜Oh＜0．005的实验条件范围内，液滴变形破碎模式与Oh数无明显依赖关系，而在We数相近情况下，液滴变形破碎模式呈现明显的相似性。

液-液体系;液滴变形破碎;冲击;高速摄影;We数;Oh数

0 引言

液滴与不相溶环境液体发生相对运动时，液滴会在环境液体作用下发生变形乃至破碎，这种现象普遍存在于各类工程实践中，如石油开采与输送中的油水两相流型演变、生物以及化工工业常见的液液雾化过程、核工业安全关心的高温熔融金属与冷却液的作用等等。研究这些过程中一个基本的问题——液-液体系中单个独立液滴的变形破碎行为，不仅有助于对工程现象的把握和预测，同时也是对建立在液-液体系上的液滴变形破碎相关机理认识的有效补充。

对单个液滴的变形破碎行为的研究由来已久，但过去的研究多集中于气－液体系。在早期研究中，Lane［1］，Hinze［2］和Hanson等［3］利用高速摄影拍摄到单个液滴在连续高速气流作用下的变形破碎图像，发现了几种具有典型特征的变形破碎模式，同时揭示了这些模式与Weber数（简称We数）和Ohnesorge数（简称Oh数）之间的相关性。随后诸多学者对单个液滴在气流作用下的变形破碎行为进行了更为深入的研究［4－17］。Pilch和Erdman［18］，Gelfand等［19］，Guildenbecher等［20］对气－液体系中单个液滴变形破碎行为的研究成果进行总结归纳，得到了一些被普遍认同的结论：首先，液滴变形破碎模式大致可分为振荡、袋状、花蕾状、剪切破碎、坍塌破碎等几种典型模式［1819］，Theofanous等［16－17］近年对这些模式的分类和主导作用机制作了进一步的修正；其次，在粘性较小即Oh数较低（通常是Oh＜0．1）的条件下，We数被认为是决定液滴变形破碎行为的主要无量纲参数。但当Oh数增大到一定程度时，Oh数和We数都对液滴变形破碎行为有着明显影响［10，18，21－23］；此外，液滴与环境流体的密度比ε也是影响变形破碎行为的一个重要参数［12，19－20］。由于气－液体系中液滴与环境气体的密度比ε普遍较大（ε～O（102）量级以上），两种密度接近的气－液体系在实验上难以实现，造成此类情况下液滴变形破碎的实验数据和认知的缺乏。

液－液体系是实现密度比ε～O（1）量级下液滴变形破碎的理想配置。相对于气－液体系已取得的大量研究成果而言，针对液－液体系研究较少见诸发表。Patel和Theofanous［24］设计了一套液体激波管用于研究单个水银液滴在水中的变形过程，并认为水－气体系中临界Bond数（简称Bo数）对水滴变形破碎的影响在水银－水体系中不明显。Hsiang和Faeth［25］设计了一套基于液－液体系的垂直坠落装置研究单个液滴在环境液体中的垂直下落过程，得到无附加扰动条件下单个液滴的变形形态。研究发现两种典型变形模式（圆台状和碗状）之间转化的临界We数随Reynolds数（简称Re数）的上升而增加。Landeau等［26］对浮力作用下液团在相溶和不相溶环境液体中的扩散行为进行了实验研究，归纳出低Oh数条件下液团扩散的几种典型模式并讨论了扩散模式与We数的依赖关系。与常规气－液体系中的液滴变形破碎不同，以上研究所关注的均非液滴快速置于相对恒定流动环境后的自由发展过程。针对这一欠缺，作者所在的实验室自行研制了一种类似于气－液体系中激波管效果的、基于液－液体系的坠落装置对水－油体系中水滴在冲击作用下的演变过程进行了实验研究，拍摄得到4种液滴典型演变模式，并分析了坠落高度和滴径对水滴在环境油相中演变模式的影响［27］。该研究突出对典型工况下水滴在环境油相中的典型演变模式的实验观察和探讨，但具体的参数化研究尚不够系统，定量分析也不够具体深入，缺乏对液－液体系中液滴变形破碎机理的有效认识和规律性总结。

本文在实验室已有的工作基础之上，针对前期工作的不足，从研究冲击作用下单个液滴在环境液体中变形破碎行为的机理出发，对影响液滴变形破碎行为的有关参数进行系统化研究和定量分析，重点关注低Oh数和一定范围We数条件下，液－液体系中单个液滴在冲击作用后的变形破碎行为。研究采用一套能施加短时间冲击作用的垂直坠落装置来实现液－液体系中液滴与环境液体的相对运动，并利用高速摄影记录冲击作用下单个液滴在环境液体中整个变形破碎行为的清晰图像，在此基础上对变形破碎模式与无量纲参数（We数、Oh数等）的依赖关系进行探究。

1 实验方法和装置

本文延续实验室前期工作的实验构思［27］，在一个充满环境液体的密封箱体内部缓慢生成液滴，然后让整个箱体自由坠落，近似自由落体的坠落过程中基本消除了因重力引起的液滴与环境液体体积力差所带来的沉浮运动，液滴在液－液体系界面张力的作用下恢复成近似圆球形。当箱体撞击到缓冲装置时，箱体及其内部液体速度迅速减速至零附近。由于液滴与环境液体的密度存在差异，使得两者的减速过程不同步，液滴与环境液体之间发生相对运动，导致液滴在环境液体动力学作用下发生变形乃至破碎。

在继承已有实验装置重复性较好、便于实现液滴与环境液体相对运动、降低高速摄影拍摄行程等优点［27］的基础上对实验装置进行改进，主要包括加速度信号采集系统、光源以及缓冲装置，以便于定量分析和规律性总结。改进后的垂直坠落装置如图1所示。该装置具体由坠落系统（见图1（a））和记录系统（见图1（b））2部分组成。其中，坠落系统主要由液滴生成装置、密封箱体、不锈钢滑轨以及细沙缓冲装置构成，利用绳索和定滑轮控制箱体的坠落高度，绳索扣解除后箱体自由坠落完成一组实验；记录系统由高速摄影（MikrotronTMMC1311 CCD）、LED阵列光源、加速度传感器以及示波器构成，采用背光拍摄，曝光时间1／10000s，获得1000帧／s，分辨率为512× 1280的液滴变形破碎行为连续照片，同时利用示波器记录冲击过程中箱体的加速度信号。

图1 实验装置示意图Fig．1 Schematic of experimental setup

针对实验室前期工作中粘度测量缺失、冲击加速度曲线记录不系统等定量测量问题，本文中将对相关实验参数做系统性的定量测量工作。为尽可能获得丰富的参数范围，实验中环境液体选择1，2－丙二醇与水按质量配比生成的混合溶液，液滴选择全氯乙烯或者全氯乙烯与ExxsolTMD110白油按体积配比生成的混合溶液。采用浮子密度计和毛细管粘度计分别测量液滴和环境液体的密度和粘度，通过悬滴法［28］测得液滴与环境液体之间的界面张力，记录每组实验工况的冲击加速度曲线。测量得到的相关物性参数范围如表1所示，不同坠落高度的冲击加速度曲线如图2所示（图中冲击加速度单位g为重力加速度）。

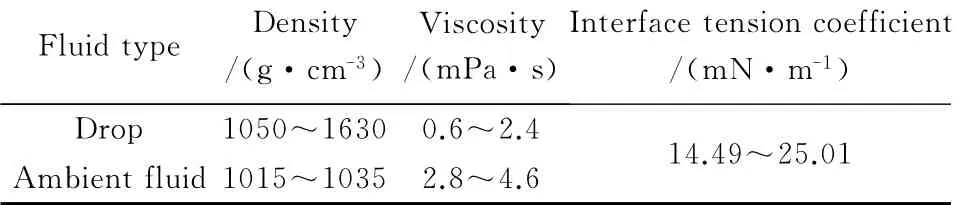
表1 液滴与环境液体的相关物性参数Table 1 Related properties of drop and ambient fluid

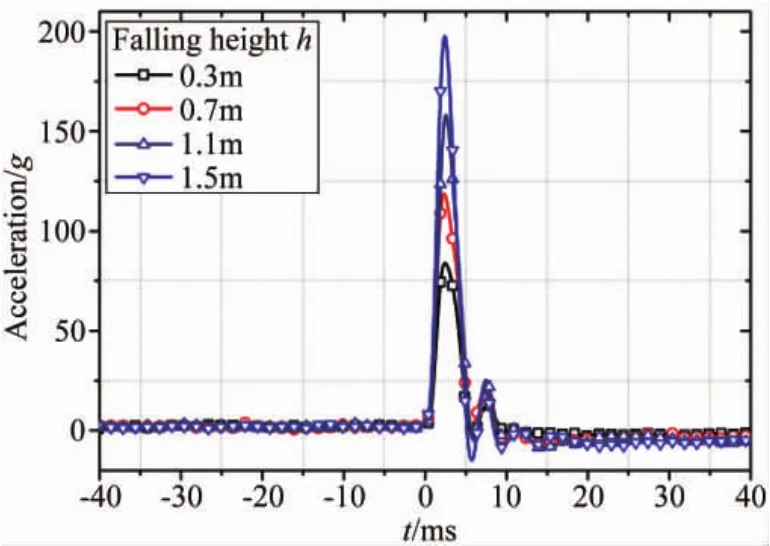
图2 不同坠落高度的冲击加速度曲线Fig．2 Impact acceleration curves of different falling heights

液滴由储液瓶流经导管再通过点胶针头的针管生成（见图1）。通过调整点胶针头的针管直径以及液滴与环境液体的物理性质（主要是两者的界面张力系数）来控制液滴直径的大小。实验中液滴初始直径范围为4．0～9．0mm。其中，液滴密度、粘度，环境液体密度、粘度，液滴的初始直径，箱体坠落高度以及液滴与环境液体之间的界面张力系数分别记为ρd，μd，ρa，μa，d0，h和σ。

表2 液滴5种典型变形破碎模式所对应的实验条件Table 2 Typical experimental conditions for five modes of drop deformation and breakup

2 实验结果与分析讨论

2．1 液滴典型变形破碎模式

通过改变液滴和环境液体的物理属性、装置坠落高度、液滴直径等实验条件，本文开展了一系列的单个液滴变形破碎实验。利用高速摄影拍摄得到5种液滴典型变形破碎模式清晰序列照片，如图3所示，其中0时刻与图2相同。按照变形破碎行为的激烈程度依次为振荡模式（见图3（A））、袋状模式（见图3（B））、帽状模式（见图3（C））、竹节状模式（见图3（D））和蘑菇状模式（见图3（E））。其中帽状、竹节状以及蘑菇状破碎模式在已有的气－液体系的研究中尚未见到。5种液滴典型变形破碎模式所对应的实验条件如表2所示。从图3中可以看出，振荡和袋状模式中液滴仅有凹陷、膨胀等简单变形，并没有观察到液膜破碎现象，属于较温和的变形行为，液－液界面拓扑结构未发生改变；而帽状、竹节状和蘑菇状模式中，液滴内部出现汇聚环状射流、环状射流卷起、环状射流翻转等复杂变形（如图4所示，图中阴影部分为液滴，其余为环境液体，红色箭头表示环状射流的发展方向和趋势），并伴随液膜破碎现象，液－液界面拓扑结构发生显著改变。

为明确区分上述5种模式，本文将对这几种典型模式中液滴变形破碎行为各自的特点进行简明刻画。振荡模式中，液滴上表面逐渐变平并持续向下发展形成凹陷（见图3（A）40ms），凹陷没有贯穿液滴下表面形成液膜，随后凹陷回弹恢复（见图3（A）80ms），液滴反复振荡；袋状模式中，凹陷向下发展直至触及液滴下表面形成液膜（见图3（B）40ms），液膜持续向外膨胀，液滴中部形似一个袋状腔体（见图3（B）60ms），随后液膜中止膨胀并逐渐回缩（见图3（B）100ms）；帽状模式中，凹陷上部周围液滴在赤道附近向腔体内部汇聚发展生成环状射流（见图3（C）35ms）。环状射流持续向下汇聚发展，射流前缘部分逐渐聚拢合并（见图3（C）65ms和4（a）），液滴整体此时形似倒转的“帽子”，随后液膜破碎分散成微小液滴（见图3（C）80ms）；竹节状模式中，向腔体内部持续向下发展的环状射流后续没有聚拢合并，而是向外扩张并卷起见（见图3（D）30ms和4（b）），液滴主体部分此时形似“竹节”，随后出现液膜破碎现象（见图3（D）35ms）；蘑菇状模式中，环状射流卷起的前缘出现二次翻转（见图3（E）10ms），后续液滴上部不断拉长，同时液滴中部出现明显的横向收缩，形成类似“蘑菇”状的外部轮廓（见图3（E）20ms和4（c）），随后出现液膜破碎现象（见图3（E）30ms）。

图3 液滴5种典型变形破碎模式序列图：（A）振荡模式；（B）袋状模式；（C）帽状模式；（D）竹节状模式；（E）蘑菇状模式Fig．3 Sequential images showing five modes of drop deformation and breakup：（A）oscillatory mode；（B）bag mode；（C）cap mode；（D）bamboo mode；（E）mushroom mode

2．2 液滴变形形态的相似性

分析无量纲参数对液滴变形破碎模式的影响有必要首先对同一变形破碎模式下液滴形态的相似性进行考察。

通过改变液滴尺寸、物性以及坠落高度等参数，可以获得相似的液滴变形破碎模式。图5和表3分别给出了3种液滴典型变形破碎模式的3组相似性对比照片，以及变形形态图片所对应的实验参数。对比分析可以得出以下初步结论：（a）液滴初始直径、液滴与环境液体的密度比和粘度比、界面张力系数以及坠落高度等实验参数之间存在一定的等效性，调节这些实验参数可以得到相似的液滴变形破碎模式；（b）袋状、帽状、竹节状等典型变形破碎模式是变形程度由弱到强的一种较为普遍的演变形式。

图4 液滴内部结构剖视图：（a）帽状模式；（b）竹节状模式；（c）蘑菇状模式Fig．4 Structures of the deforming drop：（a）cap mode；（b）bamboo mode；（c）mushroom mode

图5 液滴变形形态相似性验证图：（a1）～（a3）袋状模式；（b1）～（b3）帽状模式；（c1）～（c3）竹节状模式Fig．5 Similarity verification of drop deformation：（a1）～（a3）bag mode；（b1）～（b3）cap mode；（c1）～（c3）bamboo mode

参照前人在气－液体系中认为液滴变形破碎行为主要与We数、Oh数有一定依赖关系的观点，从验证液－液体系中是否存在相似依赖关系的角度出发，本文将3组变形形态相似照片对应的We数、Oh数分别提取汇总，如图6所示。从图中可以看出，当液滴变形形态相似时，对应的We数较为接近，而Oh数则有一定区别。可以认为，在实验范围内，液滴变形破碎模式的相似性与We数有较强关联，与Oh数关系尚不明显。

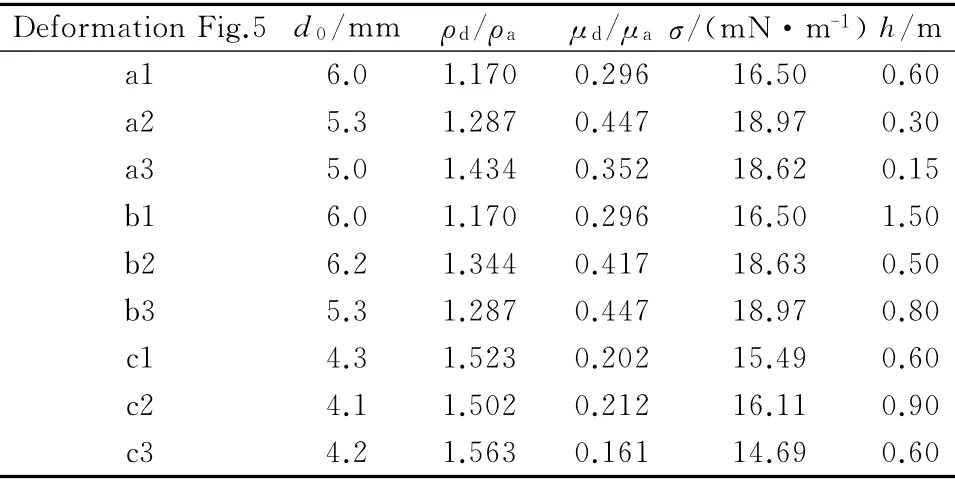
表3 图5所对应的实验参数Table 3 Corresponding experimental conditions for the results of Fig．5

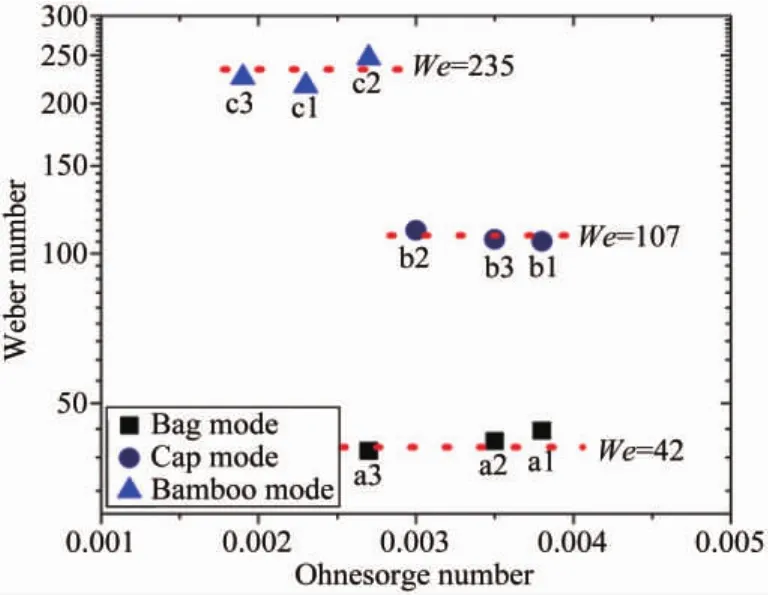
图6 液滴变形形态相似性与无量纲参数的对应关系Fig．6 Relationship of non－dimensional parameters and drop deformation images

2．3 液滴变形破碎模式与无量纲参数的依赖关系

由于液滴典型变形破碎模式之间的转变是一个渐变过程，因此有必要借助过渡模式来表征各个典型变形破碎模式之间的转变，进而利用过渡模式划分液滴变形破碎模式，绘制相应的模式分布图来进一步揭示液滴变形破碎模式与无量纲参数的依赖关系。

在分析大量实验图片之后，发现液滴在发生变形破碎行为时会卷入周围的环境液体，而液体处于不同变形破碎模式下所卷入的环境液体体积不尽相同。在较温和的变形模式中，卷入体积随着变形程度的加剧明显增加，而在剧烈变形模式中，卷入体积的增长趋势并不明显，因此本文选取无量纲卷入体积比Vamax／V0作为划分液滴变形剧烈程度的一个初步判据。其中，Vamax为液滴卷入的最大环境液体体积，V0为液滴初始体积。根据卷入过程的轮廓遮光效果，应用图像处理方法分别提取Vamax和V0，并建立无量纲卷入体积比Vamax／V0与We数的依赖关系，如图7所示。从图中可以看出，处于阴影部分即帽状模式中的Vamax／V0值随We数的增加大部分散布于约1．5～2．5范围内，这与其他模式Vamax／V0散点值的分布规律有明显区别。左侧振荡和袋状模式中，Vamax／V0值随We数的增加呈明显上升趋势；而右侧竹节状和蘑菇状模式中，Vamax／V0值随We数的增加则基本稳定地散布于约2．0～2．5范围内。基于此，本文选取从袋状到帽状模式以及从帽状到竹节状模式之间转变的2种过渡模式作为分界点进行模式划分，进而建立液滴变形破碎模式与无量纲参数之间的依赖关系。

图7 Vamax／V0与We数的依赖关系图Fig．7 Relationship of Vamax／V0and the Weber number

图8 液滴变形破碎模式之间的转变过程图像，上行：（a）袋状模式，（b）过渡模式，（c）帽状模式，（b＊）过渡模式剖视图；下行：（d）帽状模式，（e）过渡模式，（f）竹节状模式，（e＊）过渡模式剖视图Fig．8 Transition between drop deformation and breakup modes，upper row：（a）bag mode，（b）transition mode，（c）cap mode，（b＊）cross－sectional view of transition mode；lower row：（d）cap mode，（e）transition mode，（f）bamboo mode，（e＊）Cross－sectional view of transition mode

图8 给出了2种液滴变形破碎模式之间转变过程以及2种过渡模式中液滴内部结构剖视图。从图8（a）～（c）中可以看出，袋状模式中袋状腔体内部没有生成环状射流；袋状－帽状过渡模式（见图8（b＊））中环状射流刚刚生成，射流方向竖直向下，没有向内持续发展趋势；而帽状模式中环状射流已持续向内汇聚发展；从图8（d）～（f）中可以看出，帽状模式中环状射流前缘部分逐渐聚拢合并；帽状－竹节状过渡模式（见图8（e＊））中环状射流前缘没有聚拢合并而是向外水平扩张，没有向上卷起的趋势；竹节状模式中环状射流前缘已明显向外扩张卷起。

图9给出了以上述2种过渡模式划分的We－Oh液滴变形破碎模式分布图。从分布图中可以看出，液滴变形破碎模式与Oh数无明显依赖关系，随着Oh数的增加，液滴变形破碎模式无明显变化；但随着We的增加，液滴变形破碎模式的递进趋势则十分明显，可见We数此时为液滴变形破碎模式的主要控制参数。鉴于本文实验中Oh数处于较低的Oh＜0．1范围，以上结论与Pilch和Erdman［18］归纳的气－液体系中Oh＜0．1条件下的临界We数与Oh数的关系大致类似。

图9 We－Oh液滴变形破碎模式分布图Fig．9 We－Oh modes map for drop deformation and breakup

3 结 论

基于液－液两相体系的垂直坠落装置，研究了单个液滴在环境液体中的变形破碎行为。通过改变液滴和环境液体的物理属性、调节装置坠落高度、控制生成液滴大小等途径实现一定可调范围的实验条件，以获得较为丰富的液滴变形破碎行为演变模式。

基于本文实验结果，可概括以下几点认识：

（1）通过改变实验条件，本文拍摄到5种液滴典型变形破碎模式，随着变形破碎行为的加剧，分别为振荡模式、袋状模式、帽状模式、竹节状模式和蘑菇状模式。其中振荡和袋状模式中液滴只有凹陷、膨胀等简单变形，属于变形行为；而帽状、竹节状和蘑菇状模式中液滴内部出现汇聚射流、射流卷起、射流翻转等复杂变形，并伴随出现液膜破碎现象，属于变形破碎行为。

（2）通过对液滴变形形态相似性的分析发现，液滴初始直径、液滴与环境液体的密度比和粘度比、界面张力系数以及坠落高度等实验参数之间存在一定的等效性，液滴变形形态的相似性与We数有较强关联，与Oh数关系尚不明显。

（3）对液滴变形破碎模式与We数（1＜We＜700）、Oh数（0．001＜Oh＜0．005）的依赖关系进行了归纳总结，发现液滴变形破碎模式与Oh数无明显依赖关系，液滴变形破碎模式主要由We数决定，这与Pilch和Erdman［18］归纳的气－液体系中Oh＜0．1条件下的临界We数与Oh数的关系基本一致。

本文工作一方面旨在揭示液－液体系中液滴变形破碎机理，另一方面也可为多相流数值模拟研究提供第一手的实验数据参考。

［1］Lane W R．Shatter of drops in streams of air［J］．Ind Eng Chem，1951，43（6）：1312－1317．

［2］Hinze J O．Fundamentals of the hydrodynamic mechanism of splitting in dispersion processes［J］．AIChE Journal，1955，1（3）：289－295．

［3］Hanson A R，Domich E G，Adams H S．Shock tube investigation of the breakup of drops by air blasts［J］．Phys Fluids，1963，6（8）：1070－1080．

［4］Simpkins P G，Bales E L．Water－drop response to sudden accelerations［J］．J Fluid Mech，1972，55（4）：629－639．

［5］Krzeczkowski S A．Measurement of liquid droplet disintegration mechanisms［J］．Int J Multiphase Flow，1980，6（3）：227－239．

［6］Wierzba A，Takayama K．Experimental investigation of the aerodynamic breakup of liquid drops［J］．AIAA Journal，1988，26（11）：1329－1335．

［7］Yoshida T，Takayama K．Interaction of liquid droplets with planar shock waves［J］．Trans ASME J Fluids Engng，1990，112（4）：481－486．

［8］Wierzba A．Deformation and breakup of liquid drops in a gas stream at nearly critical Weber numbers［J］．Experiments in Fluids，1990，9（1）：59－64．

［9］Hsiang L P，Faeth G M．Near－limit drop deformation and secondary breakup［J］．Int J Multiphase Flow，1992，18（5）：635－652．

［10］Hsiang L P，Faeth G M．Drop properties after secondary breakup［J］．Int J Multiphase Flow，1993，19（5）：721－735．

［11］Liu Z，Reitz R D．An analysis of the distorsion and breakup mechanisms of high speed liquid drops［J］．Int J Multiphase Flow，1997，23（4）：631－650．

［12］Joseph D D，Belanger J，Beavers G S．Breakup of a liquid drop suddenly exposed to a high－speed airstream［J］．Int J Multiphase Flow，1999，25（6）：1263－1303．

［13］Lee C H，Reitz R D．An experomental study of the effect of gas density on the distortion and breakup mechanism of drops in high speed gas stream［J］．Int J Multiphase Flow，2000，26（2）：229－244．

［14］Joseph D D，Beavers G S，Funada T．Rayleigh－Taylor instability of viscoelastic drops at high Weber numbers［J］．J Fluid Mech，2002，453：109－132．

［15］Theofanous T G，Li G J，Dinh T N．Aerobreakup in rarefied supersonic gas flows［J］．Trans ASME J Fluids Engng，2004，126（4）：516－527．

［16］Theofanous T G，Li G J，Dinh T N，et al．Aerobreakup in disturbed subsonic and supersonic flow fields［J］．J Fluid Mech，2007，593：131－170．

［17］Theofanous T G，Li G．On the physics of aerobreakup［J］．Phys Fluids，2008，20（5）：052103．

［18］Pilch M，Erdman C A．Use of breakup time data and velocity history data to predict the maximum size of stable fragments for acceleration－induced breakup of a liquid drop［J］．Int J Multiphase Flow，1987，13（6）：741－757．

［19］Gelfand B E．Droplet breakup phenomena in flows with velocity lag［J］．Progress in Energy and Combustion Science，1996，22（3）：201－265．

［20］Guildenbecher D R，Lopez－Rivera C，Sojka P E．Secondary atomization［J］．Experiments in Fluids，2009，46（3）：371－402．

［21］Majithia A K，Hall S，Harper L，et al．Droplet breakup quantification and processes in constant and pulsed air flows［C］／／Proceedings of the 22nd Conference on Liquid Atomization and Spray Systems（ILASS－Europe），Como Lake，Italy，2008．

［22］Kulkarni V，Sojka P E．Bag breakup of low viscosity drops in the presence of a continuous air jet［J］．Phys Fluids，2014，26（7）：072103．

［23］Mohit J，Surya P R，Gaurav T，et al．Secondary breakup of a drop at moderate Weber numbers［J］．Proceedings of the Royal Society A，2015，147：20140930．

［24］Patel P D，Theofanous T G．Hydrodynamic fragmentation of drops［J］．J Fluid Mech，1981，103：307－323．

［25］Hsiang L P，Faeth G M．Drop deformation and breakup due to shock wave and steady disturbances［J］．Int J Multiphase Flow，1995，21（4）：545－560．

［26］Landeau M，Deguen R，Olson P．Experiments on the fragmentation of a buoyant liquid volume in another liquid［J］．J Fluid Mech，2014，749：478－518．

［27］熊燃华，许明，李耀发，等．液－液两相介质中液滴在冲击作用下的演变过程［J］．中国科学：物理学力学天文学，2010，40（6）：773－780．

Xiong R H，Xu M，Li Y F，et al．The deformation and breakup of a drop－in－liquid under an impact loading［J］．Science China Phys，Mech and Astron，2010，40（6）：773－780．

［28］Andreas J M，Hauser E A，Tucker W B．Boundary tension by pendant drops［J］．J Phys Chem，1938，42（8）：1001－1019．

Deformation and breakup behaviors of a drop in ambient liquid under im pact

Liao Bin1，2，Zhang Guifu1，Wang Luhai1，Zhu Yujian1，*，Yang Jiming1
(1．Department of Modern Mechanics，University of Science and Technology of China，Hefei 230027，China;2．College of Architecture and Civil Engineering，Anhui Polytechnic University，Wuhu Anhui 241000，China)

In this study，we carry out an experimental investigation of the behaviors as well as the mechanism of the liquid-liquid drop deformation and breakup process following an impact．With high speed photography，five distinct deformation and breakup modes are captured，for which the key factors that dominate the transition are quantitatively analyzed．The results show that similar deformation behaviorsmay occur for a proper combination of drop sizes，density ratios between drop and ambient fluid，interfacial tensions and free falling heights．Two non-dimensional parameters，i．e．Weber number(We)and Ohnesorge number(Oh)，are calculated to estimate these effects．It is found that，similar deformation behaviorsmay have a strong correlation with theWeber number．After a further survey of the test range of present study(1＜We＜700，0．001＜Oh＜0．005)，it can be concluded that the deformation and breakup pattern is barely affected by the Ohnesorge number，whereas exhibits a strong dependence on theWeber number．

liquid-liquid system;drop deformation and breakup;impact;high speed photography;Weber number;Ohnesorge number

O359+．1

A

（编辑：张巧芸）

1672-9897(2016)05-0009-08

10．11729/syltlx20160029

2016-02-02;

2016-04-15

国家自然科学基金项目(11572313);安徽省高等教育提升计划省级自然科学研究一般项目(TSKJ2015B03)

*通信作者E-mail:yujianrd@ustc．edu．cn

Liao B，Zhang G F，Wang L H，et al．Deformation and b reakup behaviors of a d rop in ambient liquid under impact．Journal of Experiments in Fluid Mechanics，2016，30(5):9-16．廖斌，张桂夫，王鲁海，等．冲击作用下液滴在环境液体中的变形破碎行为．实验流体力学，2016，30(5):9-16．

廖 斌（1985－），男，江西抚州人，博士研究生。研究方向：实验多相流体力学。通信地址：安徽省合肥市蜀山区黄山路443号中科大西校区（230027）。E－mail：liaobin＠mail．ustc．edu．cn