二阶Fredholm 积分微分方程的有限差分—配置法

覃燕梅，罗卫华，孔 花，张 莉

(1．内江师范学院四川省高等学校数值仿真重点实验室/数学与信息科学学院，四川内江641112; 2．四川师范大学数学与软件科学学院，四川成都610064)

二阶Fredholm 积分微分方程的有限差分—配置法

覃燕梅1，罗卫华1，孔 花1，张 莉2*

(1．内江师范学院四川省高等学校数值仿真重点实验室/数学与信息科学学院，四川内江641112; 2．四川师范大学数学与软件科学学院，四川成都610064)

针对二阶Fredholm积分微分方程，提出了一种新的有限差分配置法．该方法的关键思想在于利用中心差分和分片线性Lagrange插值函数，将奇异核分裂成有限项，并用分部积分克服了奇异性．通过分析，给出了对应的代数方程组，证明了代数方程组的解的存在唯一性和收敛性．通过多个数值算例验证了所给方法的有效性．

配置法;有限差分;Fredholm积分微分方程;Lagrange插值

带Cauchy核或Hadamard核的奇异积分微分方程是计算的许多问题，如:力学［1］、热弹性力学［2－3］和机翼问题［4］等的重要模型．

众所周知，由于积分的奇异性，除了一些特定的情况，这些方程的精确解通常无法获得．因此，这些模型的数值方法成为了研究热点．

近几十年来，关于Fredholm积分微分方程带不同边界条件的数值解一直被研究．M．Gulsu等［5］利用第二类切比雪夫多项式，提出用配置方法求解方程(1)，其中Maleknejad等［6］通过Taylor级数展开和Galerkin方法，数值求解了带Cauchy核的一阶Fredholm积分微分方程;X．Yang等［7］针对四阶偏积分微分弱奇异方程，引入了Crank－Nicolson/quasi－wavelets方法; A．V．Andreev［1］采用正交高斯—雅可比公式［8］，给出了一阶强奇异积分微分方程的数值解．关于方程(1)的数值方法还可参加文献［9－16］．

本文利用 Lagrange插值多项式，研究带有Cauchy/Hadamard核的Fredholm奇异积分微分方程边界条件为:其中为正整数，s≠t，K(x，y)∈ C［a，b］，u(x)是未知函数．

1 有限差分配置法

在区间［a，b］上，定义剖分:JN={xn|xn=a+为步长，N为给定正整数．当所选基函数为分片线性多项式时，这些网格点也是配置点．

记ui=u(xi)．根据中心差分公式，方程(2)中的可以表示为

分段线性Lagrange插值多项式uh(x)近似代替u(x):

在配置点xk，k=2，3，…，N处可以变形为

其中

方程(6)中的前2项

本文重点讨论奇异积分Δ1和Δ2的数值计算方法．由(5)式可得

和

由(10)、(11)式和分部积分公式，经过一些简单的代数运算，可得

因此，综合(4)、(6)、(7)和(12)式，原方程(2)可以离散为

在(13)式中的O(h2)舍去，并将(5)式代入(13)式可得近似方程为

其中，Ai－1，Bi－1，Ci－1，i=2，3，…，N为对应的系数向量．记 A=(A1，A2，…，AN－1)T，B=(B1，B2，…，BN－1)T，C=(C1，C2，…，CN－1)T，则(13)式可转化为线性方程组:

其中F=FF+AA+BB+CC，且记z=y－x2，r=y－xN，

由于N+1阶方阵B比较复杂，下面将逐行给出其计算格式:

第1行:

第k行:(k=2，3，…，N－2)

第N－1行:

矩阵C:

定理1 线性方程组(16)的解存在唯一，且|ui

证明 首先容易知道矩阵珘A可逆，且

由K(x，y)的连续性，可知存在常数c＞0，使得

记H=A+B+C，用A－1左乘H可得

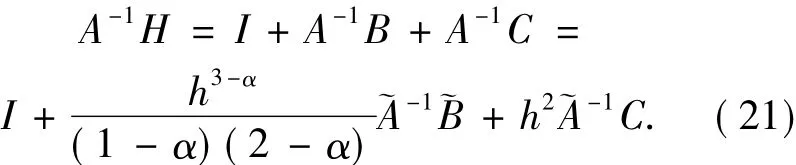
根据(19)式可知矩阵 珘B与 h无关，进一步结合(20)式和可得:当h充分小时，I严格对角占优．从而H可逆，且‖H－1‖有界，故线性方程组(16)的解存在且唯一．

假设U=(u2，u3，…，uN)T为方程组(13)的解．将(13)和(14)两式相减，可得

根据‖H－1‖的有界性，可得

2 算例

下面通过多个数值算例验证所给的有限差分配置方法的有效性．

用En表示L∞范数下配置点xi，i=1，2，…，N+ 1处产生的误差，收敛率

例1

精确解为:u(x)=x2，x∈I=［－1，1］．

例2

精确解为:u(x)=x2，x∈I=［－1，1］．

例3精确解为:u(x)=x2，x∈I=［－1，1］．

表1 例1的结果Table 1 Result of example 1

表2 例2的结果Table 2 Result of example 2

表3 例3的结果Table 3 Result of example 3

表1～3的结果表明:本文所给的有限差分配置方法具有O(h2)精度，且其误差收敛率与α无关，进而验证了定理1的正确性．

3 结语

本文针对二阶Fredholm奇异积分微分方程，基于分片线性Lagrange插值多项式，结合中心差分和配置法，提出了一种有限差分配置方法．推出了相应的代数方程组，通过多个数值算例，验证了方法的有效性．数值结果表明:所给方法在配置点能达到二阶精度，且与α取值无关．

致谢 内江师范学院重点科研项目(14ZA02)对本文给予了资助，谨致谢意．

参考文献

［1］ANDREEV A V．Development of direct numerical integration methods for one－dimensional integro－differential equations in mechanics［J］．Mechanics of Solids，2007，42(2):209－222．

［2］LADOPOULOS E G．Singular Integral Equations:Linear and Non－linear Theory and Its Applications in Science and Engineering［M］．Berlin，Heidelberg，New York:Springer－Verlag，2000．

［3］LADOPOULOS E G．Non－linear singular integral equations in elastodynamics［J］．Singular Integ Eqns，2000，2000:509－532．

［4］LUO W H，HUANG T Z，LI H B，et al．A numerical method and efficient preconditioner for generalized airfoil equations［J］．Appl Math Comput，2013，219(24):11451－11459．

［5］GULSU M，OZTURK Y．Numerical approach for the solution of hypersingular integro－differential equations［J］．Appl Math Comput，2014，230(2):701－710．

［6］MALEKNEJAD K，ARZHANG A．Numerical solution of the Fredholm singular integro－differential equation with Cauchy kernel by using Taylor－series expansion and Galerkin method［J］．Appl Math Comput，2006，182(1):888－897．

［7］YANG X，XU D，ZHANG H．Crank－Nicolson/quasi－wavelets method for solving fourth order partial integro－differential equation with a weakly singular kernel［J］．J Comput Phys，2013，234(2):317－329．

［8］IOVANE G，LIFANOV I K，SUMBATYAN M A．On direct numerical treatment of hypersingular integral equations arising in mechanics and acoustics［J］．Acta Mechanica，2003，162(1/2/3/4):99－110．

［9］SHAW R E，GAREY L E．A shooting method for singular nonlinear second order Volterra integro－differential equations［J］．Inter J Math Math Sci，1997，20(3):589－598．

［10］IURIE N C，FAQIH F M．Approximate solution of singular integro－differential equations in generalized Holder spaces［J］．Numer Algor，2007，45:205－215．

［11］XU Y，ZHANG H．Multiple positive solutions of a m－point boundary value problem for 2nth－order singular integro－differential equations in Banach spaces［J］．Nonlinear Analysis，2009，70(9):3243－3253．

［12］张阳，薛运华．求解一类高阶线性Fredholm积分微分方程Tau方法［J］．高等学校计算数学学报，2005，27:1－5．

［13］韩惠丽，朱莉．Legendre多小波数值求解Fredholm积分－微分方程(英)［J］．宁夏大学学报(自然科学版)，2011，32(4): 301－304．

［14］魏金侠，单锐，刘文，等．CAS小波法求解高阶弱奇异非线性积分微分方程数值解［J］．合肥工业大学学报(自然科学版)，2012，35(9):1293－1296．

［15］陈一鸣，刘丽丽，孙璐，等．Adomian分解法求解非线性分数阶Fredholm积分微分方程［J］．应用数学，2013，26(4):785－790．

［16］单锐，魏金侠，张雁．Bernstein算子矩阵法求高阶弱奇异积分微分方程数值解［J］．华侨大学学报(自然科学版)，2012，33(5):595－600．

A Finite Difference-collocation Method for Second-order Fredholm Integro-differential Equations

QIN Yanmei1，LUO Weihua1，KONG Hua1，ZHANG Li2

(1．Key Laboratory of Numerical Simulation in the Sichuan Province Colleges and Universities/ College of Mathematics and Information Science，Neijiang Normal College，Neijiang 641112，Sichuan; 2．College of Mathematics and Software Science，Sichuan Normal University，Chengdu 610064，Sichuan)

In this paper，based on the central difference and piecewise linear Lagrange interpolation function，a finite differencecollocation method is presented for second-order linear Fredholm integro-differential equations．The corresponding algebraic equations are obtained．Three numerical examples are employed to illustrate the effectiveness of the proposed technique．

collocation method;finite difference;Fredholm integro-differential equation;Lagrange interpolation

O242．21

A

1001－8395(2016)04－0531－05

10．3969/j．issn．1001－8395．2016．04．013

(编辑 周 俊)

2016－01－31

国家自然科学基金(11301257)和四川省教育厅青年基金(15ZA0288、16ZB0300和11ZB083)

*通信作者简介:张 莉(1982—)，女，讲师，主要从事偏微分方程数值解的研究，E－mail:lizhang_hit@163．com

2010 MSC:65M70