一个混沌系统的单输入指数自适应同步分析
2016-07-24邓奎彪范永青柳州职业技术学院广西柳州545006西安邮电大学自动化学院陕西西安700
邓奎彪,范永青(.柳州职业技术学院,广西柳州 545006;.西安邮电大学自动化学院,陕西西安 700)
一个混沌系统的单输入指数自适应同步分析
邓奎彪1,范永青2
(1.柳州职业技术学院,广西柳州 545006;2.西安邮电大学自动化学院,陕西西安710210)
摘要:首先引入一个含有乘积项系统参数的混沌系统.对新的吸引子的基本性质用相图、平衡点及稳定性、李亚谱诺夫指数谱、分岔图、Poincaré截面进行了详细分析.然后对系统参数都为正时的系统的界进行了估计,并给出系统界的表达式.由于系统中含有乘积项参数,当参数未知时,同步新系统会比较困难.文中用一个带有自适应参数更新的单输入控制器取得了系统的同步.最后,用数值仿真验证提出方法有效性.
关键词:指数同步;混沌系统;单输入;自适应
0 引言
自Lorenz在1963年发现了第一个混沌系统,即Lorenz混沌模型[1]以来,混沌奇特的非性线现象引起了国内外的学者广泛关注,混沌在众多领域取得了巨大而深远的影响,并且许多新的混沌系统相继被提出[2-6].在混沌的诸多特性中,混沌系统的界对混沌的同步与控制有极为重要的意义.然而混沌系统的界并不易求得,只能估计少量混沌系统界,如Lorenz系统[7],Lorenz系统族[8-9],Chuan系统[10]等.本文首先引入一个含有乘积项的混沌系统,分析了其基本的动力学特性.然后,构造一个适当的正定函数结合Lagrange函数法给出了新系统界的估计.作为界估计的应用,本文设计出一个带自适应的单输入线性反馈控制器实现了系统的指数同步,由于系统中含有乘积耦合项的系数,那么对于参数未知的自适应同步就非常困难,目前国内外很少有文献[11]关于有乘积耦合项系数自适应同步的报道.
1 新的混沌系统
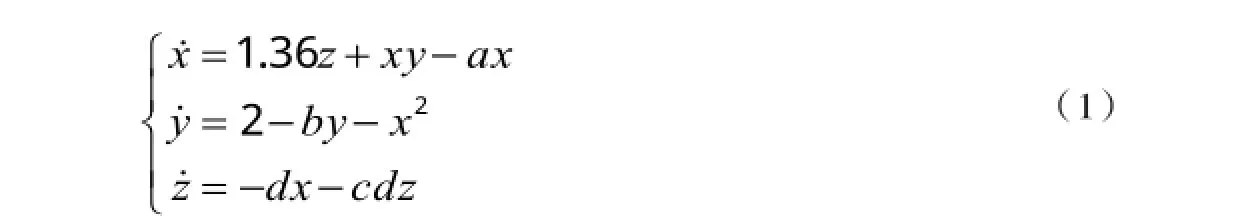
式中:x,y,z代表系统的状态变量,a,b,c,d是系统参数,且都是正的实常数.系统中有两个非线项,并有一个参数乘积项cd.当a=0.6,b=0.4,c=1.2d,d=1.5时,三个李氏指数为L1=0.178,L2=0,L3=-0.718.系统(1)有一个混沌吸引子,此混沌的三维相图见图1.

图1 系统(1)相图
1.1平衡点和稳定性
只需求解a=0.6,b=0.4,c=1.2d,d=1.5在方程组

就能得到平衡点。易求E1(0,5,0),E2(1.1431,1.7333,-0.9526),E3(-1.1434,1.7333,0.9526),三个平衡点.在平衡点E1处线性化系统(1)得到雅可比矩阵为:

由特征方程|λI-J(E1)=0,易求得三个特征值λ1=4.0514,λ2=-1.4514,λ3=-0.4 .因为有λ2,λ3<0,λ1>0,所以平衡点E1是不稳定的鞍点.同理可求出在平衡点 E2,E3处的三个特征值为别为 λ1=-1.403,λ2=0.1681+1.8221i,λ3=0.1681-1.8221i .此时在平衡点E2,E2是不稳定的鞍焦点.
1.2随参数变化分岔图,Lyapunov指数谱
分岔图和Lyapunov指数谱可表明系统状态随参数变化时的情况.下面只讨论参数b变化情形,其它参数与之类似,故不再一一讨论.固定参数a=0.6,c=1.2,d=1.5,改变参数b.当参数b∈[]0.1,0.4时,系统的分岔图和Lyapunov指数谱如图2和图3.图2说明当数b变化时系统(1)从倍周期进入混沌状态.图3表明随着b变化时的过程中周期轨和混沌交替出现. 1.3 Poincaré截面图

图2 b变化时的分岔图

图3 b变化时的Lyapunov指数
系统的混沌动力学特性还可以用Poincaré截面图来进行分析.对Poincaré截面的选取应该恰当,既不能包含系统的轨线,也不能与轨线相切.经分析计算,得系统在x=0截面上的Poincaré截面图如图4所示.显见在这Poincaré截面上的映射点集具有分形结构的密集点,吸引子的叶片清晰可见,表明新系统具有分形的特点.

图4 Poincaré截面图
以上的分析说明新的系统的确满足混沌的基本特征,众所周知混沌的运动轨线始终局限在一个确定的区域内,因而混沌吸引子是一定有界的,下面来估计混沌系统的界.
2 混沌系统界的估计
在混沌的诸多特征中,具有正的Lyapunov指数和有界的轨道这两个特征是目前广泛采用的混沌判据.前面得出了典型系统具有正的Lyapunov指数,本节对新系统的界进行估计,给出当参数a,b,c,d全为正数时系统界的表达式,从而证实了新系统具有正的Lyapunov指数并且有界这两个混沌的基本特征.


证明:选取如下的正定函数

对(4)式沿着系统(1)的轨迹求导,有


构造如下形式的的Lagrange函数
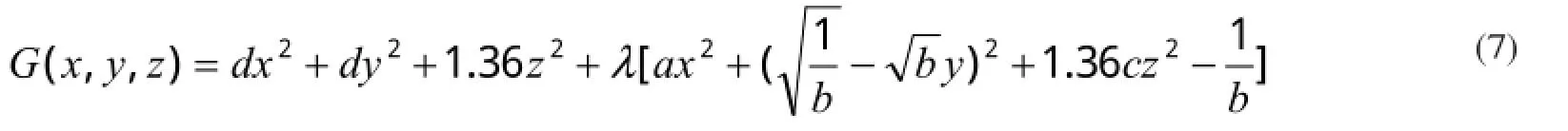
对式(7)求导,分别令

总结上面的四种情况,令

则定理1的证明完成.


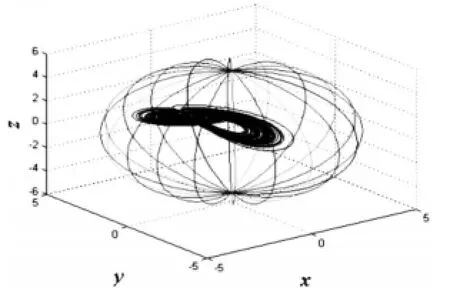
图5 系统(1)含在椭球体内
3 指数自适应同步新的混沌系统
本节将研究指数自适应同步问题,设系统(1)是驱动系统,相应的响应系统为:

式中x1,y1,z1是系统的状态变量,u是要设计的使得系统(1)和(13)取得指数自适应同步的控制器,a1,b1,c1,d1是响应系统(13)中未知需要估计的系统参数.系统(1)和系统(13)之间的误差失量E和参数误差失量Ep分别定义为:

由系统(1)和(13)得到系统误差为:

定义1指数同步:如果控制器U和参数更新规则能使得下式

成立。则称系统(1)和系统(13)取得指数同步.上式中的A,B是两个正数,V=eTpe是一个二次多项式,PT=P∈R7×7是一正定矩阵,e=[E,EP]TB为指数收敛率.
引理(算术几何平均不等式)对于任意的实数X,Y及正实数ε都有成立.

线性反馈增益k满足

参数更新规则为
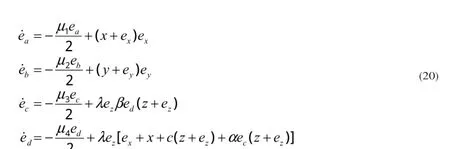
式中α,β是正的实数,且α+β=1,μ1,μ2,μ3,μ4〉0,那么驱动系统和响应系统自适应指数同步.
证明:构造如下的Lyapunov函数

对V1求导得

将式(18)(20)代入(22)有

根据式(12)和引理1,有
当下面的条件满足时
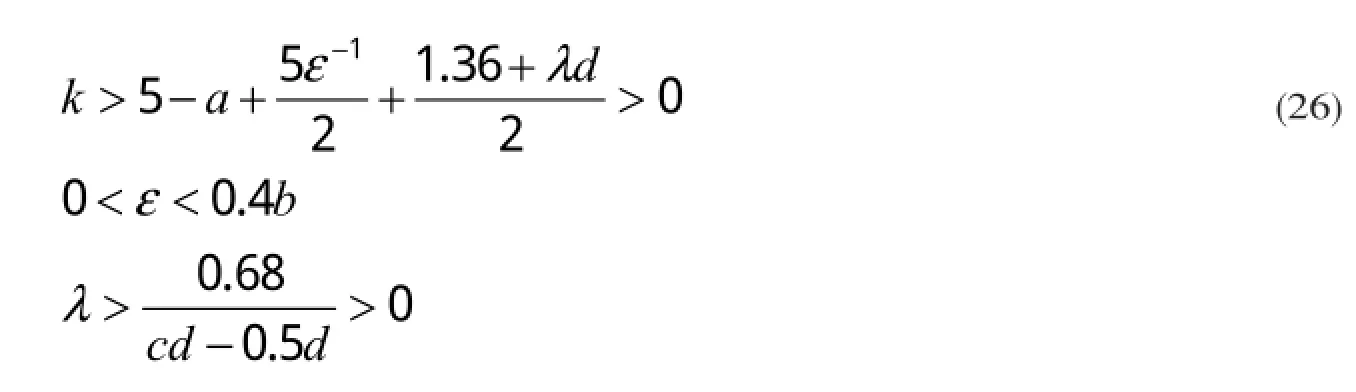

由微分知识求得V1〈V1(0) e-tδ,且V1(0)〉0根据定义1有ex,ey,ez,ea,eb,ec,ed指数收敛到0.因此在控制器(18)和参数更新规则(20)的作用下驱动系统(1)和响应系统(13)取得了指数自适应同步.
4 数值仿真
本节用数值仿真验证以上提出理论的正确性.采用四阶Runge-Kutta法求解系统(1)和系统(13),仿真步长为0.0001.系统(1)的参数值为,初始值系统令(13)初值,估计参数初值令式(20)中的参数,由式(26)要求,选取满足条件的反馈增益k=34.选定式(20)中的,我们选取(28)中的指数收敛率δ=0.15那么由定理2得时有均指数收敛到0即有,由图(6)可见在控制器(18)和参数自应律(20)的作用下驱动系统(1)和响应系统(13)很快达到指数同步,并且也实现对响应系统未知参数的识别.
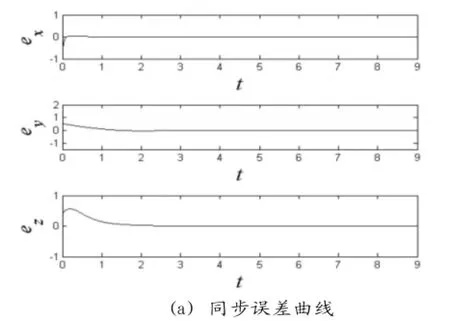

图6 系统(1)和(13)实现了指数自适应同步
5 结论
首先分析了系统的基本动力学性质,其次,通过构造一个正定函数结合Lagrange乘法确定系统(1)在参数都为正数的情形下的界.最后,设计了一个带有自适应参数更新的单输入控制器取得了系统的同步.由于只有一个单输入控制器,相比多个输入的控制器,不仅能降低控制成本,而且在工程上更容易实现.因此本文的提出的同步方法,在理论上和工程实践应用中都具有重要的价值.
[参考文献]
[1]LORENZ E N.Deterministic no-periods flow[J].Journal of the atmospheric sicence,1963,20(2):130-148.
[2]ROSSLER O E.An equation for continuous chaos[J].Phys Lett A,1976,57(5): 397-398.
[3]SPROTT J C.Some simple chaotic flows[J].Phys Rev E,1984,50(2):647-650.
[4]CHEN G R,Ueta A.Yet another chaotic Attractor[J].Inter J Bifur chaos,1999,9(7):1465-1466.
[5]LIU C X,LIU T,LIU L,et al.A new chaotic attractor[J].Chaos,Solitons and Fractals,2004,22(5):1031-1038.
[6]DENG K B,LI J,YU S M.Dynamics ananysis and synchronization of a new chaotic attrator[J].Optik-international journal for light and electron optics,2014,125(13):3071-3075.
[7]LI D M,LU J A,WU X Q,et al. Estimating the bounds for the Lorenz family of chaotic systems[J].Chaos,Solitons and Fractals,2005,23 (2): 529-534.
[8]YU P,LIAO X X.New estimation for globally attractive and positive invariant set of the family of the Lorenz systems[J].Inter J Bifur Chaos,2006,16(11):3383-3390.
[9]SUN Y J. Solution bounds of generalized Lorenz systems[J].Chaos,Solitons and Fractals,2009,40(2):691-696.
[10]LIAO X X,YU P,XIE S L,et al.Study on the global property of the smooth Chua's systems[J]. Inter J Bifur Chaos,2006(10):2815-2841.
[11]YANG C C.Exponential synchronization of a new Lorenz-like attrator with uncertain parameters via single input[J]. Applied mathematics and computation,2011,217(14):6490-6497.
(责任编辑:李洁坤)
The Analysis of a Single Exponential Input Adaptive Synchronization of a Chaotic System
DENG Kuibiao1,FAN Yongqing2
(1. Liuzhou Vocational & Technical College,Liuzhou,Guangxi,545006 China;2. School of Automation,Xi'an University of Posts and Telecommunication,Xi'an,Shaanxi,710121 China)
Abstract:This paper firstly presents a chaotic system including a product term of system parameters. Basic dynamical properties of the attractor are demonstrated in terms of phase portrait,equilibria and stability,Lyapunov exponent spectrum,bifurcation diagram and poincaré mapping. Then,the bound of this system is estimated for all the positive values of its parameters and the expression of the bound is illustrated. Owing to a product term of system parameters,it can be predicted that synchronization of the new system becomes more difficulty by taking account of uncertain system parameters. In this paper,the exponential synchronization between two identical chaotic systems by applying single input controller associated with system parameter update laws is proposed. At last,numerical studies are provided to illustrate the effectiveness of the presented scheme.
Key words:exponential synchronization;chaotic system;single input;adaptive
中图分类号:TP911-34;TP29
文献标识码:A
文章编号:2096-2126(2016)01-0113-07
[收稿日期]2016-01-10
[基金项目]国家自然科学基金资助“带有伸缩器和饱和器的模糊自适应控制设计方法研究”(61305098);广西教育厅自然科学基金资助“物联网中数据融合和安全问题关键技术研究”(KY2015YB399)。
[作者简介]邓奎彪(1970—),男,湖北荆门人,博士,工程师,研究方向:非线性控制、混沌同步、物联网技术;范永青(1978—),女,河南鹤壁人,博士,讲师,研究方向:复杂网同步控制。
