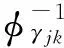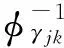不确定随机闭环物流网络的机会约束模型及性质

运蕾蕾,张兴芳

(聊城大学 数学科学学院,山东 聊城 252059)



不确定随机闭环物流网络的机会约束模型及性质

运蕾蕾,张兴芳

(聊城大学 数学科学学院,山东 聊城 252059)

摘要：提出了同时具有随机性和不确定性的闭环物流网络问题。基于机会理论,视具有随机性的参数(产地和销售地之间的单位运输成本)为具有概率分布函数的随机变量,具有不确定性的参数(客户区和销售地之间的单位运输成本及客户需求)为不确定分布的不确定变量。在产销平衡、运费及客户需求的机会约束下,建立了以闭环物流运费(不确定随机变量)的期望最小为目标的闭环物流新模型,称为不确定随机闭环物流网络的机会约束模型。给出了在特殊不确定分布下的模型性质,由此得到与其等价的具体形式。

关键词：闭环物流；不确定随机闭环物流；机会理论；机会约束

0引言

随着经济的快速发展,人们的生活水平日益提高,产品需求量的增加及交通运输的发展,产生了物流网络优化问题。随着社会的进步,人们也越来越重视经济效益和环境保护,以及废旧产品的回收和再利用。 1998年,文献[1]首次将包含废旧产品的回收和再利用的物流网络称为闭环物流网络。闭环物流网络包括：产品从产地运往销售地再到客户区的正向物流；可回收产品从客户区经销售地再运回工厂或垃圾站的逆向物流。很多学者对其进行了深入研究 ,建立了各种模型,并给出了多种解法[2-5]。文献[2]给出了闭环供应链架构及其对环境的影响。 文献[3]对废旧产品回收再制造物流网络的经营成本以及废旧资源的再利用进行了研究，建立了一个闭环物流网络优化模型。文献[4]利用混合整数线性规划的方法,提出了一种多产品、有能力限制的再制造闭环物流网络优化设计模型,并确定了网络中各种设备的数量和位置。

上述文献关于闭环物流网络的研究都假定涉及的参数是确定的。然而,在现实问题中,许多参数难以确定。当参数具有足够的样本数据时,可以用概率论进行处理。当参数没有历史的数据时,只能基于相关领域专家估计事件发生的可能性程度(或信度)来处理这种参数。主观概率和模糊集理论已经分别给出了处理专家信度的方法。文献[6-8]基于规范性公理、对偶性公理、次可加性公理和乘积公理的不确定测度提出了处理不确定性的不确定理论。目前，不确定理论已经应用到许多领域[9-11]。然而，在一个系统中往往一些不确定参数有历史的数据,而另一些没有。为解决这种既含有随机性又含有不确定性的问题,文献[8，12]提出了机会理论。目前，机会理论已经被应用到多个领域[13-14]。

本文基于机会理论，研究同时带有随机性和不确定性的闭环物流网络优化问题。在该问题中,产地与销售地之间的单位运输成本为具有概率分布函数的随机变量，客户区与销售地之间的单位运输成本和客户需求为具有不确定分布的不确定变量,以整个闭环物流的运费(不确定随机变量)的期望最小为目标,总成本小于其期望值的不确定测度,客户需求的机会和产销平衡为约束。本文将上述问题形式化,并研究特殊不确定分布下的模型性质，从而得到与其等价的具体形式。

1预备知识

定义1[6-8]如果不确定变量ξ的不确定分布φ存在反函数φ-1(α),α∈(0,1),则称不确定分布φ是正规的,且称φ-1(α)为ξ的逆不确定分布。

定义2[6-8]如果不确定变量ξ有一个不确定分布：

则称它为Zigzag不确定分布,记作Z(a,b,c),a

定义3[6-8]如果不确定变量ξ有一个不确定分布：

则称ξ为线性的,且称ξ的不确定分布为线性不确定分布,记作L(a,b),其中a,b是实数且a

定义4[6-8]若ξ是不确定变量,则称

为ξ的期望值,其中,两个积分中至少有一个是有限的。

定理1[6-8]设ξ为不确定变量,并且有正规的不确定分布φ。如果ξ存在期望值,那么

设(Γ,L,M)是一个不确定空间,(Ω,A,Pr)是一个概率空间，则称乘积(Γ,L,M)×(Ω,A,Pr)为一个机会空间。

定义6[12]设ξ是机会空间(Γ,L,M)×(Ω,A,Pr)到实数集的一个函数。如果对于任何Borel集B,Θ={ξ∈B}是L×Α的一个事件,则称ξ为不确定随机变量。

定理2[12]设f:Rn→R是一个可测函数,且ξ1,ξ2,…,ξn是机会空间(Γ,Υ,M)×(Ω,A,Pr)的不确定随机变量，则：

ξ(γ，ω)=f(ξ1(γ,ω),ξ2(γ,ω),…,ξn(γ,ω)),(γ,ω)∈Γ×Ω

是一个不确定随机变量。

定理3[12,8]设独立的随机变量η1,η2,…,ηm分别服从概率分布函数ψ1,ψ2,…,ψm,且独立的不确定变量τ1,τ2,…,τn分别有不确定分布γ1,γ2,…,γn,则不确定随机变量ξ=f(η1,η2,…,ηm,τ1,τ2,…,τn)的机会分布为：

φ(x)=∫RmF(x·，y1,y2,…,ym)dψ1(y1)…dψm(ym)，yi∈R,i=1,2,…,m，

定理 4[12,8]设η是随机变量,τ是不确定变量,a,b是常数。 则有:

E[aη+bτ]=aE[η]+bE[τ]。

2闭环物流网络的机会约束模型

2.1问题描述及符号表示

假设某生产商已经建立了一种产品的n1个生产地，计划从这些生产地向n2个销售地供货,再从销售地销往n3个客户区。为了节约成本，担负起集中回收废旧产品的义务并进行筛选,完全报废的产品运往垃圾厂集中销毁，生产地则对回收的未报废的产品进行再制造。于是正向物流和逆向物流就形成了闭环物流网络，见图1。制定从生产地到销售地、销售地到客户区、客户区到回收站及回收站到再制造站或垃圾站的最优分配运输方案，使得运费最小。

图1　闭环物流网络图

为了模型化上述闭环物流网络问题,作进一步的假设：

I：生产地/再制造站的集合,i=1,2,…,n1,i∈I。

J：备选销售地/回收站地点的集合,j=1,2,…,n2,j∈J。

K：客户区固定位置的集合,k=1,2,…,n3,k∈K。

N：备选垃圾站地点的集合,n=1,2,…,n4,n∈N。

ξk：客户区k∈K的产品需求量。它们是具有不确定分布φξk的不确定变量。

e：各客户区的废旧产品可回收率。

v:回收站j∈J废旧产品的报废率。

τij：从生产地/再制造站i到销售地/回收站j的产品单位运输成本,i∈I,j∈J。它们是具有概率分布ψτij的随机变量。

γjk：从销售地/回收站j到客户区k的产品单位运输成本,j∈J,k∈K。它们是具有不确定分布φγjk的不确定变量。

γkj：从客户区k到销售地/回收站j的可回收产品单位运输成本,k∈K,j∈J,γkj=γjk。它们是具有不确定分布φγkj=φγjk的不确定变量。

τji：从销售地/回收站j到生产地/再制造站i的可再制造产品单位运输成本,i∈I,j∈J,τji=τij。它们是具有概率分布ψτji=ψτij的随机变量。

pjn：从销售地/回收站j到垃圾站n的报废产品单位运输成本。

Iij：从生产地/再制造站i到销售地/回收站j的产品运输数量。

Ujk：从销售地/回收站j到客户区k的产品运输数量。

Qkj：从客户区k到销售地/回收站j的可回收产品运输数量。

Jji：从销售地/回收站j到生产地/再制造站i的可再制造产品运输数量。

Tjn：从销售地/回收站j到垃圾站n的报废产品运输数量。

2.2数学模型

基于上述问题的假设,总花费为：

f(x，γ，τ)=f(Iij,Ujk,Qkj,Jji,Tjn,τij，τji，γjk，γkj，i∈I,j∈J,k∈K,n∈N)=

记

根据不确定随机变量期望的性质(定理4),期望总花费为：

E[f(x,γ,τ)]=E[f1]+E[f2]+f3=

于是提出模型(a)如下：

(2)

(7)

Wi,Gj,Hn∈{0,1}， ∀i∈I,∀j∈J,∀n∈N；

(8)

Iij,Ujk,Qkj,Jji,Tjn≥0， ∀i∈I,∀j∈J,∀n∈N,∀k∈K，

(9)

其中：α,βk(>0.5),k∈K均为常数;式(1)表示不确定随机变量f小于其期望值的不确定测度不小于α；式(2)表示销售地的产品数量供应不小于客户区的产品需求量的不确定测度不小于βk；式(3)表示客户区到回收站的回收数量不小于客户需求的回收数量；式(4)～式(7)表示生产地/再制造站与销售地/回收站的正向物流量和逆向物流量守恒；式(8)～式(9)表示各变量的取值范围。

称模型(a)为不确定随机闭环物流问题的机会约束模型。注意：模型(a)的目标是不确定随机变量-总花费f的期望值最小。 所以在模型(a)中,使用了Ch{f≤E[f]}≥α作为约束。它的意义在于限制风险,这是科学的。

为了求解模型(a),下面探讨目标函数f(x，γ，τ)、式(1)、式(2)和式(3)。

因此，

定理7假设ψ(y)是随机变量f1的概率分布函数,φ(x)是f2的不确定分布函数,则式(1)等价于

证明因ψ(y)是随机变量f1的概率分布函数,φ(x)是f2的不确定分布函数,所以由定理4和定理5可知：

定理8如果不确定变量γjk=γkj有线性不确定分布L(akj,bkj),不确定变量ξk,k∈K具有Zigzag不确定分布Z(ak,bk,ck)，且βk≥0.5,则模型(a)等价于下面的模型(b)：

证明因为不确定变量γjk=γkj有线性不确定分布L(akj,bkj),所以由定理1知：

3结束语

本文假设产地和销售地之间的单位运输成本具有历史的数据,客户区和销售地之间的单位运输成本和客户需求没有历史的数据，基于机会理论,利用总成本的机会约束以及不确定随机变量的期望公式,提出了一个新的数学模型，称为不确定随机闭环物流网络的机会约束模型。提供了不确定变量具有Zigzag分布或线性分布的模型性质，并得到了与相应模型等价的具体计算形式。

参考文献：

[1]MARIN A,PELEGRIN B.The return plant location problem:modeling and resolution[J].European journal of operational research,1998,104(2):375-392.

[2]HAROLD K,IERELE B,STEEF V D V.Product modularityand the design of closed loop supply chains[J].California management review,2004,46(2):23-39.

[3]JAYARAMAN V,GUIDE V D R,SRIVASTAVA R.A closed-loop logistics model for remanufacturing[J].Journal of the operational research society,1999,50(5):497-508.

[4]代颖,马祖军,刘飞.再制造闭环物流网络优化设计模型[J].中国机械工程,2006(8)：809-814.

[5]滕志军,郭素阳,徐艳伟,等.北斗卫星导航的物流运输监控系统[J].河南科技大学学报(自然科学版),2015,36(4):47-50.

[6]LIU B D.Uncertainty theory[M].2nd ed.Berlin:Springer-Verlag,2007.

[7]LIU B D.Uncertainty theory:a branch of mathematics for modeling human uncertainty[M].Berlin:Springer-Verlag,2010.

[8]LIU B D.Uncertainty theory[M/OL].5th ed.[2015-2-18].http://orsc.edu.cn/liu.

[9]DING S B.Uncertain multi-product newsboy problem with chance constraint[J].Applied mathematics and computation,2013,223:139-146.

[10]CHEN X W,RALESCU D A.A note on truth value in uncertain logic[J].Expert systems with applications,2011,38:15582-15586.

[11]ZHANG X F,NING Y F,MENG G W.Delayed renewal process with uncertain interarrival times[J].Fuzzy optimization decision making,2013,12:79-87.

[12]LIU Y H.Uncertain random variables:a mixture of uncertainty and randomness[J].Soft computing,2013,17(4):625-634.

[13]LIU Y H.Uncertain random programming with applications[J].Fuzzy optimization and decision making,2013,12(2):153-169.

[14]YAO K,GAO J W.Uncertain random alternating renewal process with application to interval availability[J].IEEE transactions on fuzzy systems,2015,23:1333-1342.

基金项目：国家自然科学基金项目(11471152,61273044)

作者简介：运蕾蕾(1991-),女,山东聊城人,硕士生;张兴芳(1957-),女,山东聊城人,教授,硕士生导师,主要研究方向为不确定数学理论及应用.

收稿日期：2016-03-13

文章编号：1672-6871(2016)05-0071-06

DOI:10.15926/j.cnki.issn1672-6871.2016.05.016

中图分类号：O29

文献标志码：A