基于Voronoi结构的多边形单元网格生成方法

石怡婧，邵国建，丁胜勇

(河海大学 力学与材料学院，江苏 南京 210098)



基于Voronoi结构的多边形单元网格生成方法

石怡婧，邵国建，丁胜勇

(河海大学 力学与材料学院，江苏 南京 210098)

摘要：针对多边形单元网格难以生成的问题，建立了基于Voronoi结构的多边形单元网格生成方法。该方法通过区域内的一组初始点来构造Voronoi结构。对初始种子点的分布进行优化，以达到控制多边形单元网格密度的目的。利用Voronoi结构的特点，通过添加种子点对应目标区域边界的映射点对边界进行拟合，实现Voronoi结构对复杂边界的逼近。对Voronoi结构进行质心化，改善生成多边形单元形态。给出了该方法的程序实施步骤，并结合网格生成实例，验证了其合理性和可行性。

关键词：有限元法；多边形单元；网格生成；Voronoi结构

0引言

在有限元的分析过程中，由于研究对象几何结构和材质的复杂性，势必会增加建立有限元网格模型的难度。尤其对于形状比较复杂的几何形状，其网格剖分耗时较多，并且容易出错。因此，网格剖分技术是网格模型建立的核心内容，一个好的有限元网格对提高计算效率和计算精度起着关键作用。目前，对于任意形状的分析区域，三角形及四边形单元的网格生成技术已经较为成熟。而多边形单元作为一种新型的单元形式，由于其边数及形状的任意性，与常规单元相比有独特的优势。针对复杂几何体进行网格划分更加灵活、方便[1-2]，近年来受到越来越广泛的关注[3]。文献[4]提出了Delaunay多边形化生成多边形网格的技术。文献[5]将一种类似于金字塔型的方法用于划分复杂三维模型多边形网格中。文献[6]利用传统三角形有限元网格生成形状合理的多边形单元网格。文献[7]利用多边形比例边界有限元方法生成多边形网格。但是，目前多边形单元的网格生成算法还比较粗糙，生成的多边形单元网格非常畸形，处理复杂边界处的网格时，构造能较好满足多边形有限元分析的单元形状也有一定困难。

本文以Voronoi结构为基础，通过对Voronoi结构的质心化来弥补现有多边形单元网格生成方法中单元形态较差的缺陷。同时，探讨非均匀网格生成的解决方案及复杂边界的拟合问题。给出多边形单元网格自动生成程序的实施步骤，并结合具体实例来验证本文方法的合理性和可行性。

1Voronoi结构及其质心化

Voronoi图是针对平面离散点集而言，将平面分成若干个区域，各区域仅有一个点，该点所在的区域是距离该点最近点的集合[8]。Voronoi图的数学定义：记R2空间上任意两点xi和xj的欧氏距离为d(xi,xj)，P={P1,P2,…,Pn}是R2空间内互异离散点集合，设

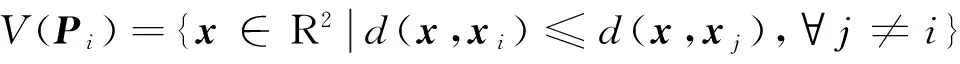
(1)

则称V(Pi)为任意点Pi(也可称为种子)的Voronoi区域，又称为Voronoi单胞。Voronoi单胞的边是集合P中某两个点连线的垂直平分线，相邻Voronoi单胞的种子点连线构成Voronoi图的对偶图，被称为Delaunay三角化。图1为Voronoi图及其Delaunay三角化。如图1所示，“+”号表示种子点，实线表示Voronoi图，虚线表示Delaunay三角化。在多边形有限元法中，可以将Voronoi单胞视为多边形单元。

图1　Voronoi图及其Delaunay三角化

一般在Voronoi图中，Voronoi单胞的种子点与其质心并不重合，此时Voronoi单胞的形状较为畸形。而质心化Voronoi图(centroidalVoronoitessellation，CVT)是Voronoi图的一种特殊形式[9-11]，其种子点与对应的Voronoi单胞的质心重合，即：

(2)

(3)

若该聚类能量函数ε(P)的值逐渐减小并收敛到一个固定值，即：

(4)

此时，生成的Voronoi图为CVT。

Lloyd算法[10]是目前广泛使用的计算CVT的一种算法，是一种必然收敛的迭代算法。由于CVT形式不唯一，所以Lloyd算法是局部收敛的。

图2为基于Lloyd算法的Voronoi结构优化过程。图2中，“+”号表示种子点，“⊙”号表示Voronoi单胞质心，在单位正方型区域内随机分布20个种子点，然后利用Lloyd算法生成CVT，优化步数k=20。图2a为初始的Voronoi结构，此时ε(P)=4.45×10-3，种子点和质心点位移差异较大，Voronoi单胞形状很差。图2b为k=2的Voronoi结构，此时ε(P)=2.74×10-3，种子点和质心点位移差异明显减小，但Voronoi单胞形状仍然比较差。图2c为k=20的Voronoi结构，此时ε(P)=2.31×10-3，种子点和质心点基本重合，Voronoi单胞形状良好。图2的优化结果显示：优化过程中ε(P)逐渐减小并趋于稳定，Voronoi单胞形状由畸形逐渐优化成比较规则的多边形。

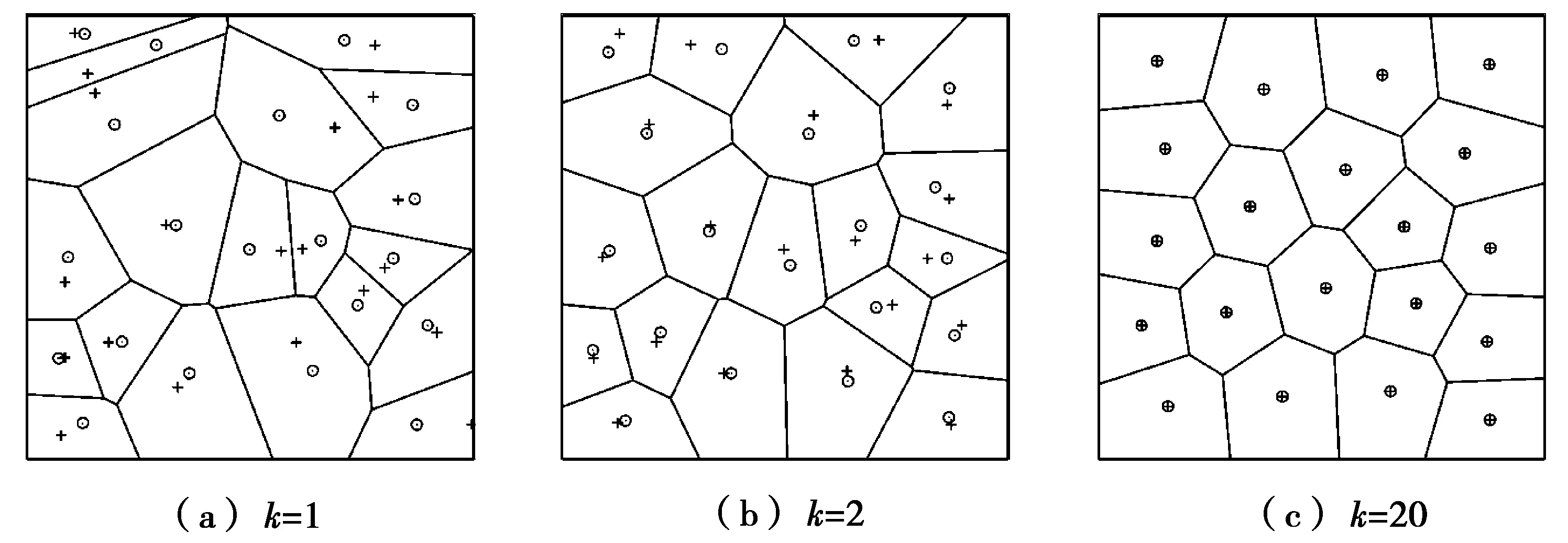
图2　基于Lloyd算法的Voronoi结构优化过程

2初始种子点分布优化

在有限元分析中，通常需要对一些重点关心区域采用更精细的网格，对一些非重点区域采用较为粗略的网格。一般初始种子点的生成都是采用随机布点的方法，这种方法会使多边形单元密度分布呈现随机化，难以满足有限元分析的要求。初始种子点的密度会在很大程度上影响最后CVT的密度，所以本文对初始种子点的分布进行优化。

本文初始种子点分布优化采用文献[12]提出的三角形网格生成算法，其基本思想是将三角形网格类比为平面弹簧结构，三角形的三条边分别对应连接种子点的各弹簧，每根弹簧的现有长度l和期望长度l0遵循力-位移关系f(l,l0)，并通过改变种子点的位置使整个结构达到平衡。图3为带圆孔的正方形区域内初始种子点优化前后的分布情况。通过图3可以看出：随着优化过程的进行，种子点分布越来越规律，步骤1到步骤2中种子点分布呈现出一定的规则性，步骤2到步骤3过程中则删除了分布在边界上的种子点。

图3　带圆孔的正方形区域内初始种子点的优化分布

3Voronoi结构边界处理

因此，可通过下式得到种子点对应的映射点：

(5)

图5为Voronoi结构的边界处理图。图5中，“+”为未映射的种子点，“∘”为映射点。对大多数种子点而言，对应映射点的存在不一定有助于最终Voronoi结构的生成，因此，需要对种子点进行筛选。将种子点Delaunay三角化，选取Delaunay三角形网格边界上的种子点即最外层种子点作为待映射的种子点，并生成其对应的最近边界处的映射点。由于上文种子点对应的Delaunay三角形网格中三角形都为锐角三角形，很容易证明只有最外层种子点与其对应的最近边界处的映射点生成的Voronoi单胞存在公共边界。

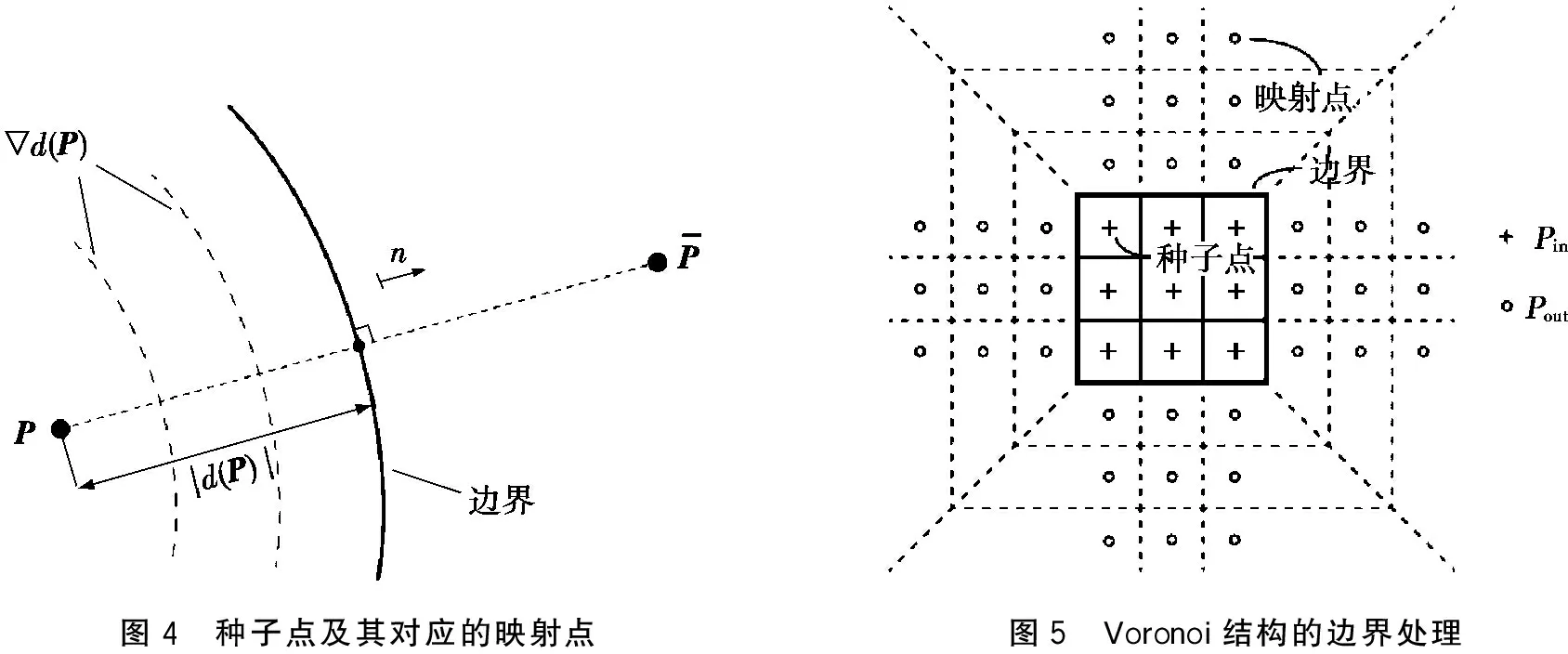
图4 种子点及其对应的映射点图5 Voronoi结构的边界处理

Voronoi结构边界生成具体步骤为：(Ⅰ)在目标区域生成种子点集Pin；(Ⅱ)筛选种子点，并进行种子点对应于目标区域边界∂Ω的映射点集Pout的生成，这些映射点位于分析区域的外部；(Ⅲ)进行点集P=Pin∪Pout对应的Voronoi结构的生成，种子点集Pin对应的Voronoi单胞集为目标区域的网格。

在步骤(Ⅲ)生成的Voronoi结构中，如果种子点和其对应的映射点有共同的Voronoi单胞边界，则所有共同边界的集合构成了目标区域边界。以带圆孔的正方形区域为例，步骤(Ⅲ)中的点集P如图6所示。图6中，“+”号表示未映射的种子点，“◇”号表示需映射的种子点，“°”号表示映射点。

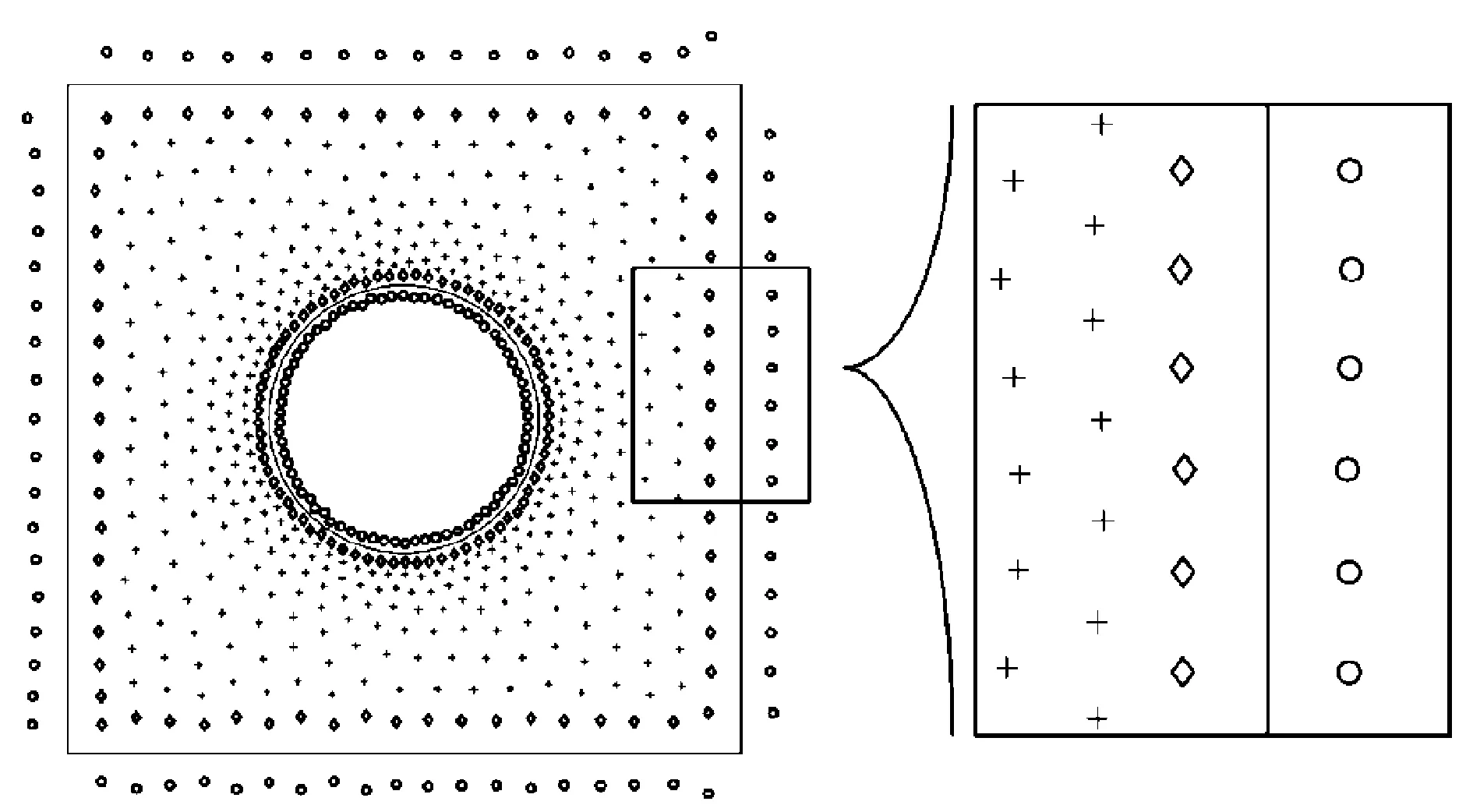
图6　筛选后的种子点和映射点分布情况

4程序实施及实例

基于Voronoi结构的多边形单元网格程序实施方案的步骤如下：(Ⅰ)在目标区域内随机生成n个初始种子点，利用初始种子点优化方法对种子点进行分布优化；(Ⅱ)利用边界处理方法对步骤(Ⅰ)获得的种子点Pin进行筛选，生成对应的映射点Pout；(Ⅲ)生成点集P=Pin∪Pout对应的Voronoi结构，利用Lloyd算法对Voronoi结构进行进一步优化，最后输出种子点Pin对应的Voronoi单胞即为最终的多边形单元网格。

实例在单位圆形区域内部挖去一个较小的圆形区域，其边界方程表达式为：

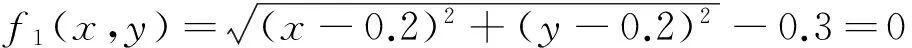
利用上述方案生成的多边形单元网格如图7所示，其中，μ表示单元内角角度的平均值，σ表示角度的标准差。

图7　基于Voronoi结构的多边形单元网格实例

图7a和图7c表明：通过本文多边形网格生成方法得到的均匀网格单元及非均匀网格单元形状都较为良好。图7b和图7d是均匀网格单元和非均匀网格单元情况下的内角角度分布规律图，不难发现单元内角角度平均值约为120°，标准差为5°～8°。通过对比均匀和非均匀网格中多边形单元内角角度的统计值可以发现：均匀网格的角度分布更集中于120°，而非均匀网格则相对略为分散，但都近似正多边形并基本符合正态分布的规律，从而验证了本文多边形网格生成方法的合理性和可行性。

5结束语

本文利用三角形网格生成算法对初始种子点分布进行合理优化，以控制网格中单元密度的分布，实现非均匀网格的生成。通过添加种子点对应目标区域边界的映射点，基于种子点与其对应的映射点具有的共同Voronoi单胞边界，构成目标区域的边界，简化了Voronoi结构对复杂边界的逼近过程。并对Voronoi结构进行质心化处理，显著改善了多边形单元形态。最后通过实例验证了本文方法可有效控制多边形网格中单元的密度分布，且获得的多边形单元形态良好并近似正多边形。

参考文献：

[1]王兆清.有理单元法研究[D].上海:上海大学,2004.

[2]LV J,ZHANG H W,YANG D S.Multiscale method for mechanical analysis of heterogeneous materials with polygonal microstructures[J].Mechanics of materials,2013,56(1):38-52.

[3]盛国雨.基于径向积分法的多边形及多面体有限元方法[D].大连:大连理工大学,2015.

[4]王兆清,李淑萍.多边形单元网格自动生成技术[J].中国图象图形学报,2007,12(7):1307-1311.

[5]SOHN D,CHO Y S,IM S.A novel scheme to generate meshes with hexahedral elements and poly-pyramid elements:the carving technique[J].Computer methods in applied mechanics & engineering,2012,201/204:208-227.

[6]蔡永昌,郭盛勇,杨健,等.多边形单元的构造新方法及实现[J].同济大学学报(自然科学版),2009,37(7):883-887.

[7]暴艳利,钟红,林皋.基于多边形比例边界有限元的重力坝地震断裂模拟[J].水电能源科学,2015,33(4):72-75,42.

[8]王兆清,冯伟.自然单元法研究进展[J].力学进展,2004,34(4):437-445.

[9]DU Q,FABER V,GUNZBURGER M.Centroidal Voronoi tessellations:applications and algorithms[J].SIAM review,1999,41(4):637-676.

[10]DU Q,EMELIANENKO M,JU L.Convergence of the Lloyd algorithm for computing centroidal Voronoi tessellations[J].SIAM journal on numerical analysis,2006,44(1):102-119.

[11]WANG J,WANG X.Edge-weighted centroidal Voronoi tessellations[J].Numerical math (theory,methods and applications),2010,3:223-244.

[12]PERSSON P,STRANG G.A simple mesh generator in MATLAB[J].SIAM review,2004,46(2):329-345.

[13]TALISCHI C,PAULINO G H,PEREIRA A,et al.Polygonal finite elements for topology optimization:a unifying paradigm[J].International journal for numerical methods in engineering,2010,82(6):671-698.

基金项目：国家自然科学基金项目(51278169)

作者简介：石怡婧(1992-),女,江苏南通人,硕士生;邵国建(1962-),男,浙江台州人,教授,博士,博士生导师,主要研究方向为计算力学与工程仿真.

收稿日期：2016-01-21

文章编号：1672-6871(2016)05-0051-05

DOI:10.15926/j.cnki.issn1672-6871.2016.05.012

中图分类号：TP391

文献标志码：A