加固配筋限值下钢筋混凝土梁正截面承载力研究

杨　娟

（招商局重庆交通科研设计院有限公司，重庆 400067）



加固配筋限值下钢筋混凝土梁正截面承载力研究

杨娟

（招商局重庆交通科研设计院有限公司，重庆 400067）

摘要：使用多年的混凝土结构或多或少出现病害，需要进行加固，但是考虑二次受力情况下RC加固梁正截面承载力计算公式尚未明确提出。文章通过分析不同初始荷载作用下增大截面法加固钢筋混凝土梁的极限破坏，研究二次受力对最大加固钢筋量及正截面承载力的影响，得到RC加固梁在加固配筋限值范围内正截面承载力计算公式。并与有限元软件分析结果进行对比验证，结果表明公式计算结果与分析结果基本一致，可为结构加固承载力计算提供参考。

关键词：钢筋混凝土梁；正截面承载力；二次受力；适合筋破坏；极限破坏

混凝土结构加固通常都存在二次受力问题，对此众多学者开展了理论和试验研究但还未形成较为一致的观点［1-3］。Kachlakev D［4］对FRP抗弯加固梁进行了4点弯曲试验，比较了CFRP和GFRP两种加固材料对加固结构行为的影响。针对受拉和受剪钢筋混凝土梁，Wu Z［5］研究了CFRP和GFRP两种加固材料混合加固的效果；在加固过程中，试验梁的受拉区底面首先粘贴CFRP片材再用GFRP布对梁进行缠绕。Pham H［6］和Ashour AF［7］等分别研究了CFRP加固技术在钢筋混凝土桥梁与连续梁上的应用，通过试验考查了加固梁的破坏机理。ShinY［8］和Wenwei W［9］分别研究了加固前的初始荷载对FRP加固的钢筋混凝土结构行为的影响。Ceroni F［10］，Tan KH［11］研究了FRP加固RC梁的裂缝问题，为了评估规范的计算公式和分析模型的有效性，Ceroni F通过试验研究了加固梁的裂缝间距和宽度并与预测值进行了比较。Tan KH［11］研究了长期和短期荷载作用下加固RC梁的开裂行为，并提供了以外荷载为变量的函数作为裂缝宽度的计算公式。针对采用CFRP和GFRP加固材料混合使用的RC加固梁，Hee Sun Kim［12］通过试验研究初始荷载和FRP粘贴顺序对结构的影响。

分析现有的研究可以看出，目前多数研究关注的重点为加固梁的性能，而考虑加固梁的最大加固量计算正截面承载力则很少涉及。基于此，本文通过分析在不同初始荷载下增大截面加固钢筋混凝土梁的极限破坏，研究二次受力对最大加固量的影响。

1　不同初始荷载下钢筋混凝土梁极限破坏分析

1.1基本假定

（1）梁截面平截面假定；

（2）在钢筋混凝土梁（RC）极限状态下，混凝土强度取抗压强度设计值fcd；

（3）在钢筋混凝土梁极限状态下，钢筋强度取抗拉强度设计值fsd；

（4）在钢筋混凝土梁极限破坏时，加固层不发生剥离破坏；

（5）不考虑受拉区混凝土受力。

1.2二次受力钢筋混凝土加固梁的极限破坏分析

结构加固前的初始荷载记为M，此时梁内钢筋应变记为εs1。如图1所示，在不卸除初始荷载的情况下对病害梁进行加固，加固后在没有对加固梁进行加载的情况下加固层钢筋纵向应力为0。当加固后并对加固梁进行进一步加载的情况下，原梁截面纵向受拉钢筋和加固层纵向受拉钢筋共同受力。选择原梁截面纵向受拉钢筋和同一水平线上的加固层纵向受拉钢筋进行分析，由梁截面平截面假定可知，在原梁加固后继续受力时，原梁截面纵向受拉钢筋应变的增量和加固层中的钢筋应变相等，此时有Δεs1=εs2，其中Δεs1为原梁截面纵向受拉钢筋应变的增量，εs2为加固层中的钢筋应变。文献［13］对最大配筋率限制如下：当一个梁的钢筋和混凝土都已确定的时候，必有一个固定的配筋率能够在梁发生极限破坏时其内的钢筋应力达到设计强度，并且在此时混凝土受压区强度也达到恰好混凝土的抗压极限强度，即为“界限破坏”，于此同时在这种极限破坏下，梁内的配筋率为梁的最大配筋率。

图1　结构加固前、后应力分布

很显然原梁截面纵向受拉钢筋应变大于加固层纵向受拉钢筋应变，即εs1+Δεs1≥Δεs1=εs2。所以加固梁极限破坏时界限破坏有3种形式：

（1） 在加固梁极限破坏时，原梁纵向受拉钢筋屈服，但加固层纵向受拉钢筋并没有达到屈服；此时由于加固层钢筋并没有达到屈服，而是受压区混凝土被压碎整个梁就破坏，为塑性破坏，并没有很大的延展性，并且造成一定的钢筋浪费，不建议使用；

（2） 在加固梁极限破坏时，原梁纵向受拉钢筋和加固层纵向受拉钢筋都屈服；并且此时受压区混凝土同时达到混凝土的抗压极限，梁的破坏模式为适筋破坏；

（3） 在加固梁极限破坏时，原梁纵向受拉钢筋和加固层纵向受拉钢筋都未屈服，而是受压区混凝土达到混凝土的抗压极限而导致梁的破坏，此时加固梁破坏时由于没有明显的征兆，在设计中一般不允许采用。

由上述分析可知，在设计及其加固过程中，应尽量使加固梁发生第2种情况，即在加固梁极限破坏时，原梁纵向受拉钢筋和加固层纵向受拉钢筋都屈服；并且此时受压区混凝土同时达到混凝土的抗压极限应变。本文针对原始荷载情况下原梁截面纵向受拉钢筋和加固层纵向受拉钢筋都屈服时加固梁的最大加固量和正截面承载力进行分析。

2　不同初始荷载下加固梁正截面承载力计算

2.1加固层配筋限值分析

由上所述，加固层配筋限制即为加固梁所有纵向受拉钢筋都屈服而受压区混凝土恰好达到抗压强度设计值时，加固层中纵向受拉钢筋的最大加固量，这时原始截面纵向受拉钢筋应力和加固层中纵向受拉钢筋抗拉强度设计值为fsd2，同时混凝土受压区的混凝土压力恰好达到混凝土的抗压极限应变值，此时原梁截面纵向受拉钢筋的实际应变为（εs1+εs2） 。并且由平衡方程得：

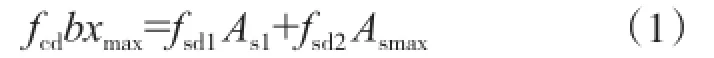
式中：b为截面宽度，xmax为最大混凝土受压区高度；fsd1为原始截面纵向受拉钢筋抗拉强度设计值，As1为原始截面纵向受拉钢筋的截面面积，Asmax为加固层中钢筋的最大加固量。

由图2平截面假设可知，最大混凝土受压区高度xmax为：

图2　加固梁界限破坏时截面应变分布图

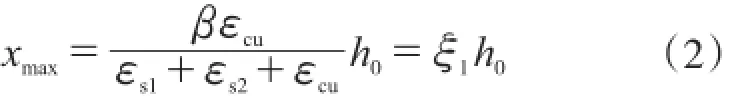
式中：β为截面受压区矩形应力图高度与实际受压区高度的比值；εcu为混凝土的极限压应变；h0为截面有效高度。

加固层中钢筋的最大加固量Asmax：

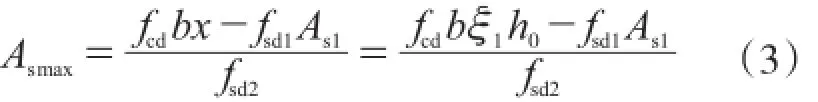
式中：β为截面宽度。

2.2二次受力RC梁正截面承载力计算公式推导

由上述分析可知，当加固层的加固量As≥Asmax时，加固梁破坏时发生超筋破坏或者加固层钢筋不屈服。当加固梁发生超筋破坏时，加固梁没有明显的破坏征兆，在设计中一般不允许采用。当加固梁发生原梁截面纵向受拉钢筋屈服而加固层钢筋不屈服时，即在加固梁发生极限破坏时，其上部受压混凝土达到极限强度，但是加固层的钢筋并不屈服，整个梁在破坏过程中并没有很大的延续，为超筋破坏，并造成钢筋的浪费。当加固层的加固量As≤Asmax时，在极限破坏时原梁截面纵向受拉钢筋和加固层纵向受拉钢筋都屈服，加固层钢筋应力亦会达到其屈服强度即σs2=fsd2，此时As为RC梁的最大加固量。因此，当加固层的加固量As≤Asmax时，加固梁正截面承载力算法简化如下。

利用平衡方程确定受压区高度x

计算加固梁的正截面承载能力

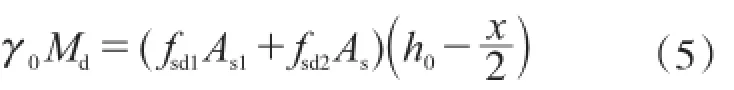
其中：γ0为桥梁结构的重要性系数，Md为弯矩组合设计值。

3　模型对比、分析与验证

为了研究不同初始荷载对加固梁承载力的影响，本文通过有限元软件对不同初始荷载作用下加固梁的破坏过程进行模拟分析，研究加固梁在极限破坏时的正截面承载力，并与上述推导公式计算结果进行对比。

3.1建模参数

本模型截面采用矩形截面，梁高300 mm，梁宽150 mm，梁长3 500 mm，原梁截面配筋如图4所示，混凝土强度等级为C30。模型中混凝土采用八节点六面体实体单元进行模拟，钢筋采用二节点桁架单元模拟。加载方式为在计算跨径三等分点上对称加载，在不同初始荷载下用1Φ20钢筋进行加固（As≤Asmax），再进行二次加载至破坏。

图4　模型梁立面与断面图（单位：cm）

3.2模型梁最大加固量及正截面承载力计算对比

利用公式（1）~（3），计算模型梁最大加固量，并与实际加固量进行对比，判断是否超筋，并与有限元模型进行对比验证。图5为在不同初始荷载作用下，通过用1Φ20钢筋对模型梁进行加固，然后再进行加载至破坏，模型梁截面纵向受拉钢筋应变图。利用上述推导公式（4）~（5），计算模型梁正截面承载力，并与有限元模型进行对比验证。图6为在不同初始荷载作用下，通过用1Φ20钢筋对模型梁进行加固，然后再进行加载至破坏，用推导公式和有限元计算的承载力对比图。

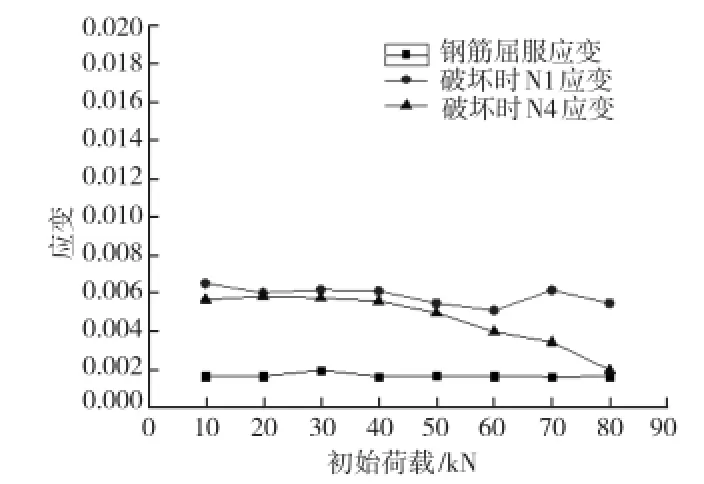
图5　有限元计算加固梁极限破坏时钢筋应变图

图6　有限元计算和公式计算加固梁承载力对比图

从图5可以看出，不管原先的初始荷载为多大，加固梁破坏时，其内部纵向受拉钢筋N1、N4都屈服，并且梁的破坏模式属于适筋破坏，与理论分析吻合。由图6可以看出，公式计算结果与模型计算结果相比偏低20%左右，由于公式计算没有考虑混凝土抗拉强度及钢筋的强化，结果偏保守。

4　结论

本文对不同初始荷载下RC梁的极限承载力进行分析，根据加固梁的极限破坏分析对加固梁的最大钢筋加固量和正截面承载力的计算公式进行推导，并利用有限元软件ABAQUS进行验证，计算结果与分析结果吻合较好。根据本文的算法，在最大加固量范围内进行加固可以使材料的强度（尤其是加固层纵向受拉钢筋的强度）得到更充分的利用；并且承载力计算过程更为简便，在实际应用中也较为便捷。

参考文献

［1］王文炜，赵国藩，黄承逵，等．碳纤维布加固已承受荷载的［1］钢筋混凝土梁抗弯性能试验研究及抗弯承载力计算［J］．［1］工程力学，2004，21（4）：172-178.

［2］张娜． CFRP加固钢筋混凝土梁规程研究及实际应用［D］．［1］大连：大连理工大学，2013.

［3］吴育後． CFRP加固梁力学性能试验研究及有限元分析［J］．［1］公路工程，2014，39（3）：271-274.

［4］Kachalakev D，Mccurry DD. Behavior of full-scale reinforced ［1］concrete beams retrofitted for shear and flexural with FRP ［1］laminates［J］. Composites: Part BEngineering，2000，31（6-7）：［1］445-452.

［5］Wu Z，Li W，Sakuma N. Innovative externally bonded FRP/［1］concrete hybrid flexural members［J］. Composite Structwes，［1］2006，72（3）：289-300.

［6］Pham H，Al-Mahaidi R. Experimental investigation into flexural ［1］retrofitting of reinforced concrete bridge beams using FRP ［1］composites［J］. Composite Strctures，2004，66（1-4）：617-25.

［7］Ashour AF，El-Refaie SA， Garrity SW. Flexural strengthening ［1］of RC continuous beams using CFRP laminates［J］. Cement & ［1］Concrete Composites，2004，2004（26）：765-775.

［8］Shin Y，Lee C. Flexural behavior of reinforced concrete beams ［1］strengthened with Carbon Fiber-Reinforced Polymer laminates at ［1］different levels of sustaining load［J］. Aci Structure Journal，［1］2003，100（2）：231-239.

［9］Wang W，Li G. Experimental study and analysis of RC beams ［1］ strengthened with CFRP laminates under sustaining load［J］. ［1］International Journal Solids & Structure 2006，43（6）：1372-［1］1387.

［10］Ceroni F， Pecce M. Cracking behavior of RC beams externally ［10］strengthened with emerging materials［J］. Construction & ［10］Building Materials，2007，21（4）：736-745.

［11］Tan KH，Saha MK. Long-term deflections of RC beams externally ［10］bonded with FRP system［J］. Journal of Composite for Construction ［10］2006，10（6）：474-482.

［12］Hee Sun Kim，Yeong Soo Shin. Flexural behavior of reinforced ［10］concrete（RC）beams retrofitted with Hybrid Fiber Reinforced ［10］Polymers（FRPs）under sustaining load［J］. Composite Structures，［10］ 2011，93（2）：802-811.

［13］张树仁，黄侨编．结构设计原理（第二版）［M］．北京：人民［10］交通出版社，2010：66.

Research on Normal Section Bearing Capacity of Reinforced Concrete Beams Strengthened under Reinforcement Boundary of Steel

Yang Juan
（China Merchants Chongqing Communications Research & Design Institute Co.， Ltd.， Chongqing 400067， China）

Abstract:The concrete structure used for many years is more or less disease， and needs to be strengthened. But the calculation formula on bearing capacity of normal section of RC beams has not been clearly stated. By analyzing the ultimate failure of reinforced concrete beams strengthened by increasing the section at different initial load， this paper studies the effects of secondary load on the maximum amount of reinforced steel and the normal section bearing capacity of RC strengthened beams，puts forward the normal section bearing capacity calculation formula of RC strengthened beam under the reinforcement steel boundary. The comparison analysis results show that the formula calculation value agrees well with finite element value， which could provide reference for structural reinforcement bearing capacity calculation.

Key words:reinforced concrete beam； bearing capacity of normal section； secondary load； failure with adequate reinforcement；ultimate failure

中图分类号：U441+.4

文献标识码：A

文章编号：1672–9889（2016）03–0043–04

收稿日期：（2016-01-26）

作者简介：杨娟（1982-），女，山东青岛人，工程师，主要从事桥梁设计工作。