约束体系对大跨度斜拉桥抗震性能的影响研究

谢群华

（东南大学建筑设计研究院有限公司，江苏 南京 210096）



约束体系对大跨度斜拉桥抗震性能的影响研究

谢群华

（东南大学建筑设计研究院有限公司，江苏 南京 210096）

摘要：文章采用非线性时程分析方法研究了地震作用下弹性约束体系和黏滞阻尼器体系对斜拉桥桥墩内力和塔顶位移的影响。结果表明，弹性约束体系和黏滞阻尼器体系均能有效地降低结构位移，但弹性约束体系墩底剪力和弯矩有所增大，设计时应予以注意。

关键词：斜拉桥；约束体系；抗震性能；桥墩内力；塔顶位移

斜拉桥主塔高、主跨大、主梁较轻、结构柔、阻尼很小，在大跨度桥梁设计中得到了广泛应用。从抗震设计的角度来看，大跨度斜拉桥塔梁连接处的纵向约束可分为4类：半漂浮体系、漂浮体系、塔梁固结体系和刚构体系。目前漂浮、半漂浮体系是斜拉桥广泛采用的两种体系。在地震荷载作用下这两种体系的内力反应较小，而位移反应较大，常常不能满足设计要求［1-4］。因此，斜拉桥抗震设计的关键，在于如何选用合适的弹性约束刚度或阻尼参数，以及如何在桥梁结构中实现［5］。基于此，本文以一大跨度斜拉桥为例，研究不同约束体系对大跨度斜拉桥抗震性能的影响。

1　工程概况

某斜拉桥的桥跨布置为80 m+185 m+500 m +185 m+80 m，为双塔单索面漂浮体系斜拉桥。主梁采用单箱三室钢箱梁，箱梁中心线梁高3.2 m，全宽35 m，梁体采用C55混凝土。索塔采用钻石型塔，塔身采用C50钢筋混凝土结构，索塔高度为121 m。索塔承台采用C40混凝土，桩基础采用C35水下混凝土。过渡墩墩身采用墩顶横向展开的花瓶实体墩，墩身为倒圆角的矩形断面，墩底断面尺寸4.8 m×3.2 m，墩顶断面尺寸5.85 m×3.2 m。

2　桥梁有限元模型

根据桥梁结构布置图，利用桥梁抗震分析软件SAP2000建立桥梁有限元模型（见图1）。计算模型以顺桥向为X轴，横桥向为Y轴，竖向为Z轴。模型中主塔、主梁、桥墩均离散为空间梁单元，其中主梁采用单梁式力学模型，并通过主从约束同斜拉桥拉索形成“鱼骨式”模型；斜拉索采用空间桁架单元，并考虑拉索垂度效应以及恒载几何刚度的影响；采用“m”法考虑桩-土相互作用［6］。采用工程场地地震安全性评价报告中提供的地震动参数，共6组地震波，计算结果取6组地震波的平均值。

图1　斜拉桥有限元模型

3　计算结果分析

3.1弹性约束体系

弹性约束体系是在主塔与主梁之间设置底索，形成弹性支承体系，主要是为了控制地震作用和运营荷载作用下主桥的梁端位移。上世纪90年代末，广东省汕头宕石大桥首次采用弹性约束索进行抗震设计后，弹性索在国内的应用逐渐增多，例如主跨312 m的芜湖长江大桥，主跨618 m的武汉白沙洲大桥等。

采用弹性约束体系进行抗震设计时，纵向弹性约束刚度的取值对斜拉桥结构整体抗震性能的影响很大。文献［7］给出了桥面系惯性力传递的计算图式（见图2）并给出了地震作用下弹性刚度的计算公式，见式（1）。

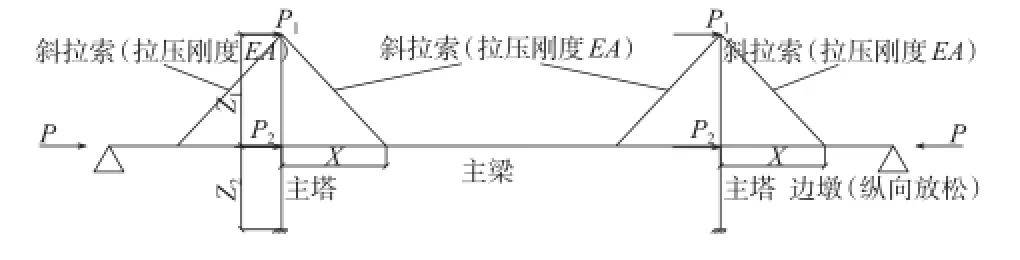
图2　地震作用下桥面系惯性力传递计算图式

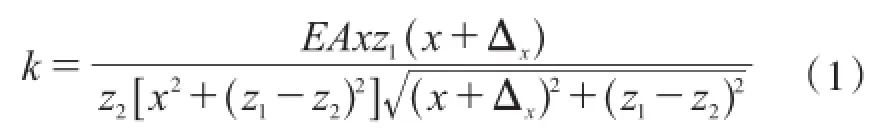
式中：x为主塔一侧主梁上的斜拉索距主塔的平均距离；z1为主塔上斜拉索锚固区距塔底的平均距离；z2为塔梁交界处的支座距塔底的距离；EA为斜拉索的平均拉压刚度；k为塔梁交接处一侧的纵向约束装置的纵向约束刚度；Δx为塔梁交接处的纵向约束装置在纵桥向所产生的线位移。

在模型的塔梁连接处设置纵向弹性支承，刚度变化范围为：1.0×103、1.0×104、5.0×104、1.0×105、5.0×105、1.0×106、1.0×1010kN/m，进行地震反应时程分析。图3给出了塔顶位移、梁端位移、塔底剪力、塔底弯矩、各墩墩底剪力和弯矩随弹性约束刚度的变化情况。由图3可以看出：

（1）塔顶和梁端位移变化规律基本一致。随着塔梁弹性约束刚度的增大，塔顶和梁端的位移迅速减小，当刚度大于1.0×106kN/m时，位移增长速度趋缓；梁端位移数值小于塔顶位移，梁端位移/塔顶位移比值介在0.63~0.88，随着弹性约束刚度的增大，两者比值减小。

（2）随着塔梁弹性约束刚度的增大，主塔塔底纵向剪力不断增大，有约束体系和无约束体系的剪力比值在1.0~1.44；当约束刚度大于5.0×104kN/m时，塔底纵向剪力增幅达16%。

（3）随着塔梁弹性约束刚度的增大，主塔塔底纵向弯矩总体上不断增大，有约束体系和无约束体系的弯矩比值在1.0~1.73，当刚度大于5.0×104kN/m时，塔底纵向弯矩增幅达33%。

（4）随着塔梁弹性约束刚度的增大，过渡墩和辅助墩的剪力和弯矩基本保持不变，有约束体系和无约束体系的剪力比值和弯矩比值均在1.0~1.02。

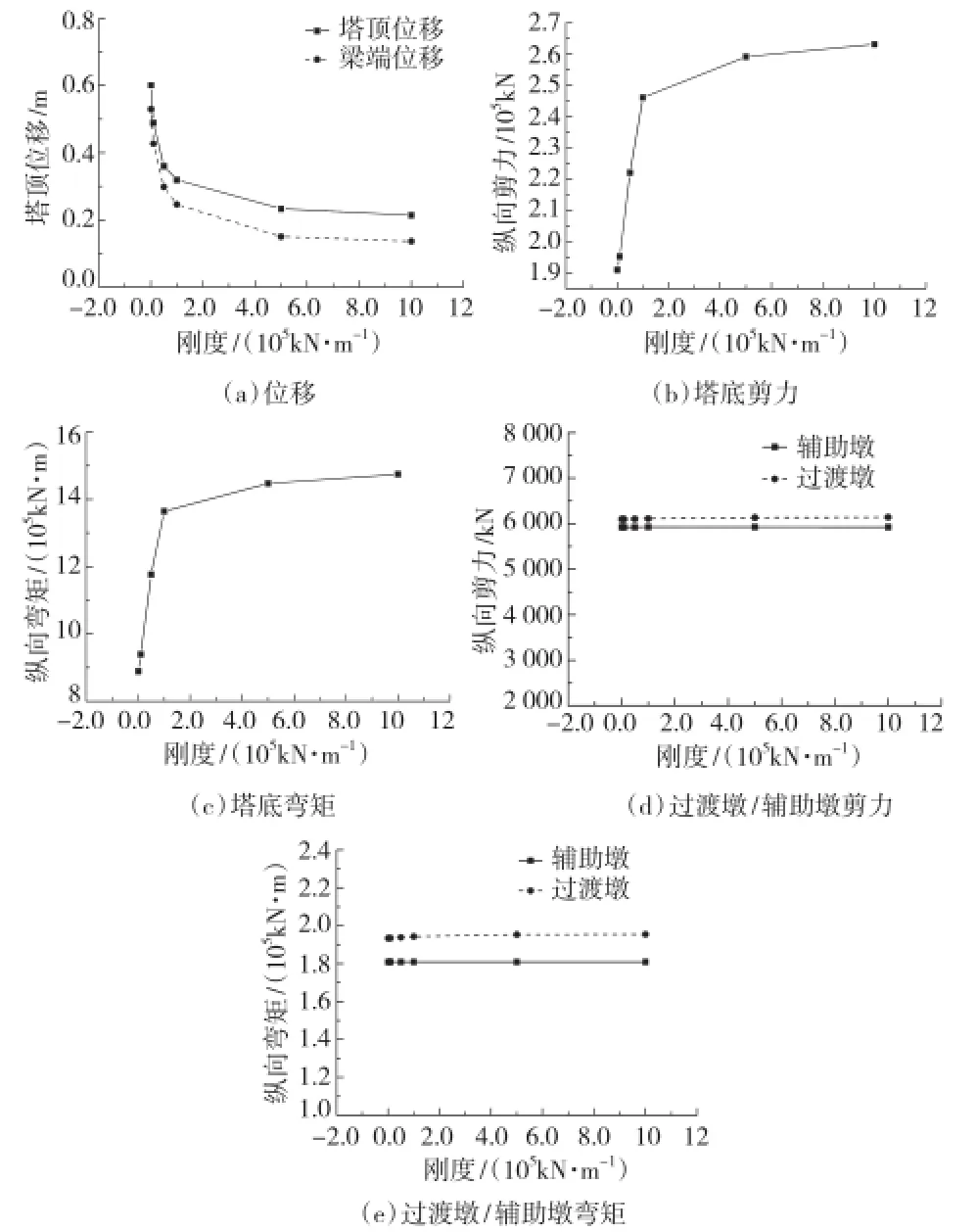
图3　不同弹性约束刚度桥梁内力响应

通过以上分析，纵向弹性约束的刚度可取为5.0×104kN/m。

3.2黏滞阻尼器体系

黏滞阻尼器是一种无刚度的速度相关型阻尼装置，其阻尼力-位移滞回曲线近似矩形，动力特性稳定，且不改变结构固有特性，不增加结构刚度，只提供附加阻尼［8］。分析时阻尼器采用Maxwell计算模型进行模拟，在该模型中，阻尼力与相对变形的速度关系为：

式中：F为阻尼力；C为阻尼系数；v为最大反应速度；α为速度指数。

分析时阻尼常数C分别取为2 000、3 000、3 500、4 000、5 000、6 000、7 000、8 000和10 000 kN/（m/s）α，阻尼指数α分别取为0.1、0.2、0.3、0.4、0.6、0.8。假设阻尼器布置在主塔处，采用非线性时程方法，比较塔顶位移、梁端位移、塔底剪力、塔底弯矩、各墩墩底剪力和弯矩随阻尼常数C和阻尼指数α的变化情况，见图4。

图4　塔底内力和塔顶位移变化曲线

由图4图可以看出：

（1）阻尼指数α一定时，随着阻尼常数C的增大，塔顶和梁端位移总体减小，当阻尼常数C大于6 000 kN/（m/s）α后，塔顶位移变化趋缓；塔顶位移最大值与最小值比值大于1.284，梁端位移最大值与最小值比值大于1.785。

（2）阻尼指数α一定时，主塔纵向弯矩和剪力随C的增大先减小后变大，纵向剪力波谷对应C值在3 000~5 000 kN/（m/s）α，纵向弯矩波谷C值在5 000~6 000 kN/（m/s）α；主塔塔底纵向弯矩最大值与最小值比值大于1.274，主塔塔底剪力最大值与最小值比值大于1.069。

（3）阻尼常数C一定时，阻尼指数α越大，塔顶位移总体上越小（C为4 000~8 000kN/（m/s）α），三者数值相差基本在11%以内，而梁端位移总体上则越大，但三者数值相差在2%以内。

（4）当C值小于4 000 kN/（m/s）α时，α值越大，主塔塔底剪力越大；当C值大于4 000 kN/（m/s）α时，α值越大；主塔塔底剪力越小。

（5）当C值小于6 000 kN/（m/s）α时，α值越大，主塔塔底弯矩越大；当C值大于7 000 kN/（m/s）α时，α值越大；主塔塔底弯矩越小。

（6）阻尼常数C和阻尼指数α对过渡墩和辅助墩内力的影响较小，最大值与最小值比值小于1.002。

综上，兼顾斜拉桥塔底受力和梁端位移的原则，阻尼器初步选取C=5 500，α=0.2组合，阻尼器只布置在两个主塔与主梁的连接处。此时，主塔塔底纵向剪力是无阻尼体系的86%，纵向弯矩为无阻尼体系的88%，辅助墩和过渡墩底剪力和弯矩基本不变，梁端位移和主塔位移大大减小，为无阻尼器方案的32%和37%。

4　结语

综上分析可知：

（1）与斜拉桥漂浮体系相比，弹性约束体系和黏滞阻尼器体系均能有效地降低塔顶和梁端位移。

（2）随着塔梁弹性约束刚度的增大，主墩墩底纵向剪力和弯矩不断增大。弹性约束刚度取5.0×104kN/m时，墩底纵向剪力增幅16%，弯矩增幅33%。

（3）采用黏滞阻尼器可以同时降低大跨度斜拉桥的位移和内力。阻尼器参数取C=5 500，α=0.2组合时，主塔塔底纵向剪力是漂浮体系的86%，纵向弯矩是漂浮体系的88%。

（4）与阻尼器体系相比，弹性约束体系造价低廉，经济性较好，但本桥弹性约束体系下塔底内力增大幅度较大。综合分析弹性约束体系与黏滞阻尼器体系，本桥选择黏滞阻尼器体系。

参考文献

［1］王志强，胡世德，范立础．东海大桥粘滞阻尼器参数研究［J］．中国公路学报，2005，18（3）：37-42.

［2］ 蒋伟，李洞明，李杨．塔梁间纵向弹性约束对斜拉桥抗震性能的影响［J］．现代交通技术，2007，4（5）：50-52.

［3］ 邬都，赵君黎，李贞新．阻尼器在我国长大桥梁建设中的应用简介［J］．公路，2009，5：112-114.

［4］Long an LI. A seismic measure for three-span cable-stayed bridge in longitudinal direction［C］∥3rd PRC-US workshop schedule，2004，Shanghai，China.

［5］张永亮，陈兴冲，郭永强．塔梁间纵向弹性约束对铁路斜拉桥动力特性及地震反应的影响［J］．铁道科学与工程学报，2011，8（2）：21-26.

［6］ 巫生平，张超，房贞政．斜拉桥粘滞阻尼器设计方案及参数回归分析［J］．桥梁建设，2014，44（5）：21-26.

［7］ 李立峰，刘本永，张晨熙，等．中等跨径斜拉桥塔梁弹性约束装置的减震效应研究［J］．地震工程与工程振动，2013，33（1）：146-152.

［8］ 陈永祁，耿瑞琦，马良喆．桥梁用液体黏滞阻尼器的减振设计和类型选择［J］．土木工程学报，2007，40（7）：55-61.

Effect Analysis of Constrained System on Seismic Performance of Long-span Cable-stayed Bridge

Xie Qunhua
（Architects & Engineers Co. Ltd. of Southeast University， Nanjing 210096， China）

Abstract:In this paper， the effect of elastic restrained system and viscous dampers system on the internal force and displacement of long-span cable-stayed bridge tower under seismic load using nonlinear time history analysis method. The results show that， the structural displacement is reduced effectively with elastic restrained system or viscous dampers system， but the shear force and bending moment of tower top are increased with elastic restrained system， which should be noticed in seismic design.

Key words:cable-stayed bridge； constrained system； seismic performance； pier internal force； displacement of tower top

中图分类号：U442.5+5

文献标识码：A

文章编号：1672–9889（2016）03–0040–03

收稿日期：（2015-07-22）

作者简介：谢群华（1980-），男，湖南娄底人，工程师，主要从事桥梁隧道设计工作。