运算放大器的动态误差分析

严刚峰，郭　兵，方　红

(1.成都大学　电子信息工程学院，成都　610106;2.四川大学　计算机学院，成都　610065)



运算放大器的动态误差分析

严刚峰1，2，郭兵2，方红1

(1.成都大学电子信息工程学院，成都610106;2.四川大学计算机学院，成都610065)

摘要由于实际运算放大器与理想运算放大器的主要参数存在较大的差别，导致实际运算放大电路存在较大的动态误差。该文采用节点电位分析法，从运算放大电路的频率特性出发，以反相积分运算放大电路为例，详细讨论了正弦输入信号和阶跃输入信号作用下，由于开环直流电压增益、增益带宽积有限而引起积分运算的动态误差。可以得出明确的结论和相应电路元件及参数的选取原则，为高精度运算放大电路动态误差的分析提供了参考，有利于高精度运算放大电路的设计。

关键词运算放大器；动态误差；电路设计

运算放大器是一种直接耦合的高增益放大器，具有体积小、可靠性高、价格较低、温度特性较好的特点[1-2]。作为电子领域中最为基本的器件之一，运算放大器广泛应用于仪器仪表的放大器、滤波器、电压/电流转换和电流/电压转换、模拟计算机等电子设备场合[3-8]。由运算放大器为核心的各种实际电路中，常常把运算放大器作为理想器件，进行应用电路的设计和分析，这固然为设计过程带来了很多便利，但实际上，性能最好的运算放大器也只能是接近理想器件，这就难免产生运算误差，使得设计出的运算放大电路运算精度不高，影响了电子产品质量的提高[2]。本文采用节点电位分析法和频率特性分析方法，以反相积分电路为例，详细介绍运算放大电路动态误差的分析过程，并通过得出的结论，给出元器件参数的选取原则。

1运算放大器的频率特性

反相积分电路示意图如图1所示，下面分析运算放大电路的开环直流电压增益Kod、增益带宽积Kodf0有限而引起积分运算的动态误差。

图1　反相积分电路示意图

设运算放大器的开环频率特性Ko(jω)是单极点的，即：

(1)

解之可得：

Ei(jω)

(2)

图2　积分放大器的渐近幅频特性曲线

首先划分频段，用两个频率点把整个频率轴分为高频段、中频段和低频段。频率特性如图2所示，运算放大器的剪切频率ωc=2πfc=2πKodf0=Kod/τ0作为高频段的频率分点；而把低频段的频率分点选择为ωL=1/(KodτRC)，这是因为用运算放大器组成的积分器相当于将积分时间常数τRC扩大了Kod倍。

1) 高频段，ω>>Kod/τ0，此时有：

式(2)可近似为：

(3)

式(2)可近以为：

E0(jω)≈-KodEi(jω)

(4)

式(2)可近以为：

(5)

综合式(3)～式(5)后，可把式(2)近似分解为：

(6)

这样把积分器近似分解成一个放大环节、两个惯性环节的串联，可大大简化动态误差的分析。

2动态误差分析

从图2的幅频特性曲线图上可知，为了使积分器正常工作，必须满足如下条件：

即必须有足够宽的中频段。实际积分器的传递函数在中频段与理想积分器的传递函数是一致的，因此，实际积分器仅在低频段和高频段产生积分误差，下面分正弦函数输入信号和阶跃函数输入信号两种情况加以分析。

1) 输入为正弦函数电压信号时的误差分析。

(7)

理想积分器的输出为：

(8)

(9)

③在高频段时，ω>>Kod/τ0，此时有1+(ωτ0/Kod)2≈(ωτ0/Kod)2，arctan(-ωτ0/Kod)≈-π/2，此时输出为：

(10)

式(10)表明，积分器已变成增益降低的同相器。

(11)

π/2，此时输出为：

(12)

式(12)表明，积分器已变成开环的反相器。

(13)

2) 输入为阶跃电压信号时的误差分析。

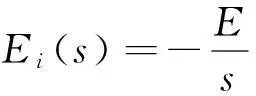
输出的时域表达式为：

(14)

理想的输出为：

(15)

3放大器及其元器件参数的选取原则

由上述分析所得结论，在设计反相积分运算放大电路时应按如下原则选取放大器及其元器件的参数。

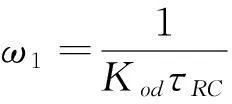
4结束语

本文采用节点电位分析法，从电路的频率特性出发。讨论了反相积分运算放大电路的动态误差，并由此得出了设计反相积分运算放大电路时，放大器及其元器件参数的选择原则，为提高运算放大电路运算精度，减小动态误差提供了参考。虽然本文仅选用反相积分运算放大电路进行了讨论，但其他类型运算放大电路的动态误差分析可以采用完全类似的方法进行分析，因此具有较好的实用价值。

参 考 文 献

[1]蔡锦福.运算放大器原理与应用[M].北京：科学出版社，2007.

[2]李春云，魏英.运算放大器参数误差分析及设计应用[J].数字技术与应用，2012(8):141-142.

[3]李琳.集成运算放大器的误差分析[J].计量与测试技术，2006(12):19-20.

[4]周作泉.双积分运算放大器的非线性误差分析[J].电气传动，1981(1):56-59.

[5]崔文孝，陈正宏，张华.集成运算放大器的误差分析[J].黑龙江电子技术，1999(4):40-42，58.

[6]查强中.运算放大器误差分析的一种简易方法[J].重庆大学学报(自然科学版)，1982(1):51-63.

[7]王书建，尹根造.共模输入电阻对同相输入运算放大器运算误差的贡献[J].河北师范大学学报，1989(1):93-95.

[8]史书田.集成运算放大器的误差分析与补偿方法[J].海军工程学院学报，1992(3):56-62.

收稿日期:2015-06-25；修改日期: 2015-07-11

基金项目：国家自然科学基金(11205022)；四川省教育厅科研项目(15ZB0384)。

作者简介：严刚峰(1977-)，男，博士后，副教授，主要从事嵌入式系统设计，随机信号处理以及系统仿真，非线性检测技术与系统方面的研究。

中图分类号TN722

文献标志码A

doi:10.3969/j.issn.1672-4550.2016.03.001

Dynamic Error Analysis of Operational Amplifier

YAN Gangfeng1，2，GUO Bing2，FANG Hong1

(1.School of Electronic Information Engineering，Chengdu University，Chengdu 610106，China;2.College of Computer Science，Sichuan University，Chengdu 610065，China)

AbstractBecause the main parameters of the actual operational amplifier and the ideal operational amplifier are different，this leads to the actual operational amplifier circuit has the dynamic error.When input signals are sinusoidal signal and step signal，by using node voltage analysis method and frequency response method，this paper discusses in detail the dynamic error of operational amplifier circuit due to the fact that open loop DC gain and gain bandwidth product are not infinite.Then one can draw a clear conclusion and the principles for selection of circuit components and parameters，which provide a reference for dynamic error analysis of high precision operational amplifier circuit.It is beneficial to design high precision operational amplifier circuit.

Key wordsoperational amplifier;dynamic error;circuit design

·实 验 技 术·