基于磁梯度张量的地下小目标相关成像方法

李金朋，张英堂，范红波，李志宁，张　帅

(1.解放军军械工程学院七系， 河北 石家庄 050003;2.解放军72465部队，山东 济南 250022)



基于磁梯度张量的地下小目标相关成像方法

李金朋1，张英堂1，范红波1，李志宁1，张帅2

(1.解放军军械工程学院七系， 河北 石家庄 050003;2.解放军72465部队，山东 济南 250022)

摘要:针对小目标铁磁物质反演方法研究中，磁总场探测包含信息不完整并且传统反演方法无法通过先验信息与目标建立联系的问题，提出了基于磁梯度张量的地下小目标相关成像方法。该方法首先利用有限元方法对铁磁目标在测量面的磁梯度张量场进行正演计算以作为实测数据；然后将地下待成像空间划分为三维规则网格并将每个网格节点等效为磁偶极子，计算每个磁偶极子在测量面产生的磁梯度张量数据与实测数据的互相关系数，作为磁偶极子在待成像空间的密度分布图；最后利用迭代计算将密度分布图转化为实际的物性参数分布图。仿真验证表明：该方法不仅能够获得地下小目标的分布情况，还能得到目标位于不同位置的实际物性参数值。

关键词:磁梯度张量；地下小目标；相关成像;迭代计算

0引言

地下小目标磁性体反演技术是通过地下磁性目标(未爆弹药、掩埋水雷等)所引起的磁异常值解算出其在地下的分布信息，其特点是定位速度快、经济性比较高，是应用比较广泛的一种目标探测方法。三维相关成像技术是一种通过计算实测磁异常与地下待成像磁偶极子扫描函数之间的归一化互相关系数来获得地下目标分布的方法。1997年由Patella首次提出将概率成像方法应用于自然电位异常的解释[1-2]。Mauriello等将概率成像法推广到大地电磁和重力领域[3-4]。国内许令周、王绪本、毛立峰等利用概率成像方法对自然电场和大地电磁数据进行了研究[5-7]，取得了一定进展。中国地质大学郭良辉等根据概率成像的概念提出重力数据的三维相关成像法并将其推广到磁场数据的相关成像，提出了磁总场异常相关成像法[8]；石磊等利用磁总场异常垂直梯度数据来解释异常源的位置，提高了成像分辨率，一定程度上改善了复杂异常的成像效果。

然而，在以上的目标反演研究中，由于磁总场探测包含信息不完整并且相关成像法所得到的结果为互相关系数分布图，无法通过先验信息与之建立联系[9]，最终影响了相关成像法在实际中的应用。针对此问题，本文提出基于磁梯度张量的地下小目标相关成像方法。

1相关成像法基本原理

笛卡尔坐标的(x,y)平面位于基准面上，z取向下为正，假设测区地下任意一点坐标为(x,y,z),体积为v的均匀磁化球体p的磁化强度为Jq，磁矩M=Jv，由于均匀磁化的球体外部磁场与位于球心的偶极子磁场等效[10]，因此我们把均匀磁化的球体视为磁偶极子。磁偶极子在测区上任意点(x,y,z)的磁总场异常B(x,y,z)可以表示为：

(1)

式(1)中，u0为真空磁导率。(xi,yi,zi)为测区第i个点的坐标，

借鉴Abdelrahman等的相邻最小二乘剩余异常的归一化互相关公式，我们定义实测磁异常与磁偶极子p在测区上的理论磁异常归一化互相关公式为：

式(2)中，(xi,yi,zi)为测区第i个观测点坐标标，B(xi,yi,zi)为该观测点实测磁异常，Bq(xi,yi,zi)为地下第q个点在该观测点的磁异常，N为测区观测点总数。

根据Schwarz不等式可知:

(3)

因此可知，公式(3)的相关系数C的的取值范围为-1≤C≤+1。其值的意义是实测磁异常由偶极子p产生的可能性。C绝对值越高，说明q点存在偶极子的可能性越大。

2基于磁梯度张量的地下小目标相关成像方法

2.1磁梯度张量要素

与传统的磁总场异常相比，磁梯度张量能提供更加丰富的异常信息，能更好地反映地下磁性体的细节特征。磁梯度张量可以由一个二阶矩阵表示为：

(4)

式(4)中,G为磁梯度张量；Bαβ(α,β=x,y,z)为磁梯度张量的分量，共有9个；根据场论可知:Bxy=Byx,Bxz=Bzx,Byz=Bzy,Bxx+Byy+Bzz=0。因此，磁梯度张量的9个分量只有5个是独立的。

根据磁总场异常三维相关成像原理，同理可推导出各磁梯度张量分量Cαβ的归一化互相关公式：

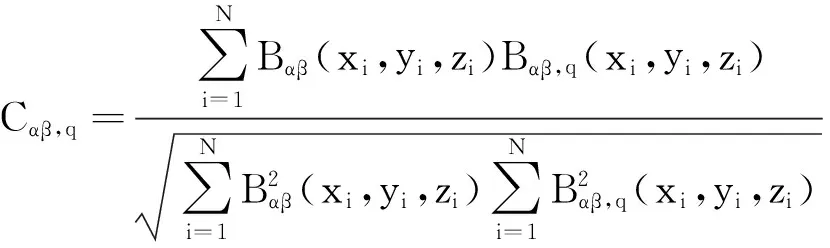
αβ=x,y,z

(5)

地下小目标三维相关成像的步骤为：

1)将地下待成像空间划分为三维均匀网格;

2)根据公式(5)求网格节点的异常与实测异常的归一化互相关；

3)将所得结果置于网格节点；

4)从浅层到深层逐层计算各网格节点的相关系数，得到相关系数数据库；

5)对数据进行可视化，获得待测小目标铁磁物质在地下的分布信息。

2.2由相关系数向实际物性参数转化

通过相关成像法计算得到的是等效的物性参数。然而，在进行反演计算时，我们更加希望获得真实的物性参数的分布。针对这一问题，根据相关成像结果与实际物性参数之间的对应关系，在相关成像结果的基础上反演物性参数。具体做法是：假设待成像区剖分后的某个节点磁偶极子磁性参数为M，通过正演计算获得位于观测面上的磁梯度张量数据Data1，并Data1与实测数据进行相关成像得到相关系数值C1；然后，用一个小的磁性参数乘C1，此时待测铁磁物质的磁性参数更新为M+C1·ΔM1；再次对该节点磁偶极子进行正演计算，获得正演数据Data2，对Data1-Data2的差值与实测数据进行相关成像获得相关系数C2。这个过程便可以理解为是反演过程中磁性参数的扰动量，而M2=M1+C2·ΔM为更新后的磁性参数值。具体流程见图1。

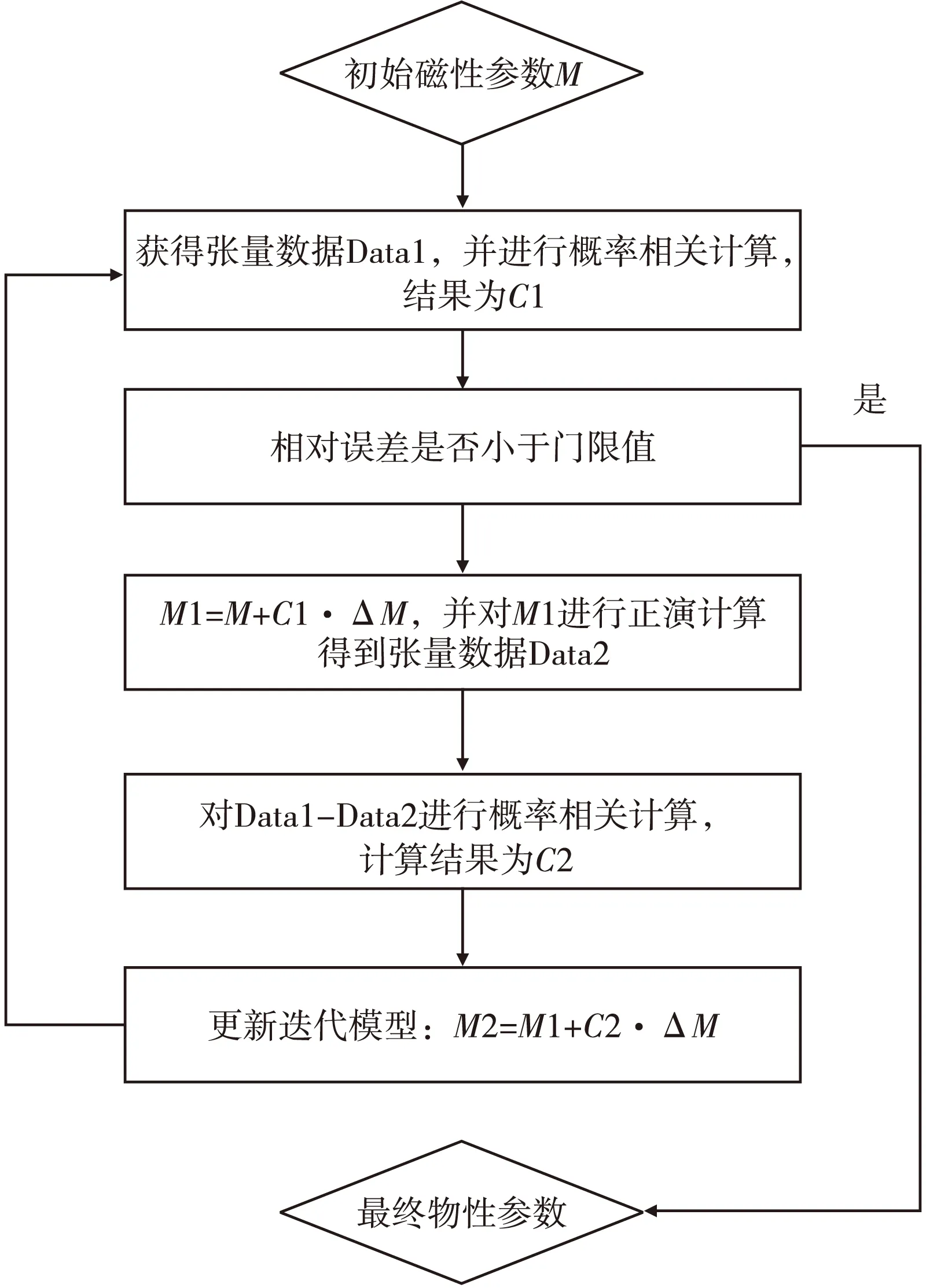
图1　相关系数到实际物性参数转化流程Fig.1　The conversion process of correlationto actual physical parameters

3仿真验证

3.1铁磁目标正演计算

本文采用COMSOL软件模拟地下未爆弹模型。COMSOL是一款通用的有限元建模软件[11-12]，利用COMSOL软件可以对未爆弹进行几何建模和网格划分。所建未爆弹模型头部为尖拱弧形，弹翼为梯形板状翼，十字布局，沿南北走向，其中心埋深距离地面3.5 m。对未爆弹模型自动网格剖分后的四面体单元数为5 333，平均单元质量为0.685 6。根据场论关系设定未爆弹的求解域属性和边界条件。在外界无电流环境下，▽×H=0，本文中设定未爆弹模型的相对磁导率为3.5，背景区域的相对磁导率为1。图2展示了未爆弹在垂直磁化作用下的磁感应强度切片图、等势面图以及磁化的方向。H为背景磁场，设定H=50 000nT。磁通密度和磁场强度的关系为B=u0(H+M)。

利用COMSOL对未爆弹模型的正演计算，以获得未爆弹位于观测面上的磁梯度张量数据。图3为对未爆弹进行正演计算后得到的位于观测面上的磁梯度张量数据分布图。

图2　未爆弹正演模型Fig.2　Forward model of UXO

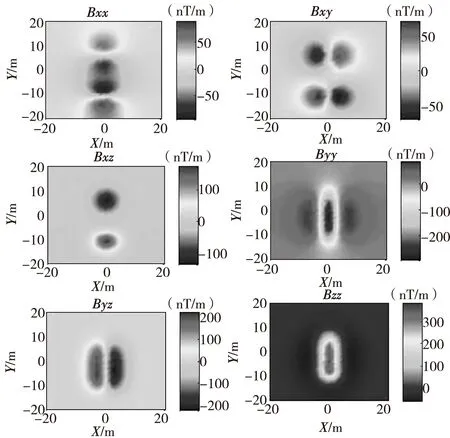
图3　未爆弹模型的磁梯度张量数据分布图Fig.3　Magnetic gradient tensor model of UXO

3.2模型测试

为验证本文反演方法的有效性，利用仿真所得磁梯度张量数据对未爆弹模型进行测试。观测面位于距地面0.1m处，反演网格间距为0.5m×0.5m×0.2m。分别对未爆弹的磁梯度张量异常Bxz，Byz，Bzz进行相关成像,图4为Z=3.5m时磁梯度张量相关成像结果图，图4(a)、(c)、(e)为相关成像结果图。图4(b)、(d)、(f)为迭代8次之后的实际物性参数成像的结果。

图4　未爆弹磁梯度数据相关成像结果Fig.4　The correlation imaging results of magnetic gradient tensor

(a)磁梯度张量加权后相关成像结果图

(b)加入先验信息后相关成像结果图

图5加入约束后反演切片图

Fig.5inversionresultssliceswithconstraint

通过图4测试的结果可以看出：未进行迭代时，在深度为3.5m处相关成像的结果出现了正的成像值，基本能够表征未爆弹的存在，但是，异常范围偏大，成像的聚焦效果较差；采用迭代计算的方法，将相关系数转换为实际的物性参数值，同时改善了聚焦效果。通过对比两个结果可以看出：本文方法的反演结果首先将相关系数转换为真正的物性参数值并获得实际物性参数的分布图；其次，改善了目标的聚焦效果，能更好的实现未爆弹的定位。

图5(a)为对不同张量信息进行加权所得到的成像结果，(b)为加入已知先验信息所得的成像结果。由于本文采用迭代计算的方法能够引入已知的地质信息作为约束。因此，可以对每一个反演数值设置解区间[Mmin,Mmax]。对于本例而言,对不同张量数据进行加权并对相对磁导率设置统一解区间为[3.2,3.8]。对比图5(a)、(b)可以看出：在反演计算中加入已知信息可以缩小解的范围，减小解的非唯一性，提高反演的分辨率；此外，通过迭代法计算所获得的物性参数值也更加接近真值。

4结论

本文提出了基于磁梯度张量地下小目标相关成像方法。该方法首先利用有限元方法对待测未爆弹模型在测量面的磁梯度张量场进行正演计算以作为实测数据；然后将地下待成像空间划分为三维规则网格并将每个网格节点等效为磁偶极子，计算每个磁偶极子在测量面产生的磁梯度张量数据与实测数据的互相关系数，作为磁偶极子在待成像空间的密度分布图；最后利用迭代计算将密度分布图转化为实际的物性参数分布图。仿真验证表明：该方法能更好的提高未爆弹的反演分辨率、改善聚焦效果，而且获得的物性参数值更加接近真实值。不足之处在于只是通过实验验证了该方法的有效性，在工程实践中的应用还有待进一步的补充和改进。

参考文献:

[1]ReneRM.Gravityinversionusingopen,reject,and“shapetotheanomaly”fillcriteria[J].Geophysics, 1986,51(4):988-994.

[2]PatellaD.Introductiontogroundsurfaceself-potentialtomography[J].GeophysicalProspecting, 1997,45(4):653-681.

[3]MaurielloP，PatellaD.PrincipleofProbabilitytomgraphyfornatural-sourceelectromagneticinductionfields[J].Geophysics,1999,64(5):1404-1417.

[4]MaurielloP，PatellaD.Localizationofmaximum-depthgravityanomalysourcebyadistributionofe-quivalentpointmasses[J].Geophysics.2001,66(5):1431-1437.

[5]许令周，关继腾，房文静.高次导数的概率成像原理[J].青岛大学学报，2003,16(4):32-36.

[6]王绪本，毛立峰，高永才.电磁导数场概率成像方法研究[J].成都理工大学学报(自然科学版)2004,31(6):679-684.

[7]王绪本，毛立峰，高永才.大地电磁概率成像效果评价[J].地球物理学报，2005,48(2):429-433.

[8]郭良辉，孟小红，石磊.磁异常ΔT三维相关成像[J].地球物理学报，2010，53(2):435-441.

[9]孟小红，刘国峰，陈召曦，等.基于剩余异常相关成像的重磁物性反演方法[J].地球物理学报， 2012，35(1):304-309.

[10]吴招才.磁力梯度张量技术及其应用研究[D].武汉：中国地质大学地球物理与空间信息学院，2008.

[11]ButlerSL.ForwardmodelingofappliedgeophysicsmethodsusingComsolandcomparisonwithanalyt-icalandlaboratoryanalogmodels[J].Computer&Geosciences,2012,42:168-176.

[12]孟慧.磁梯度张量正演、延拓、数据解释方法研究[D].吉林：吉林大学仪器科学与电器工程学院,2012.

*收稿日期:2015-11-28

作者简介:李金朋(1991—)，男，吉林长春人，硕士研究生，研究方向：目标探测与识别。E-mail:18626648671@163.com。

中图分类号:P631

文献标志码:A

文章编号：1008-1194(2016)03-0075-04

CorrelationImagingMethodofSmallSubsurfaceTargetBasedonMagneticGradientTensor

LIJinpeng1,ZHANGYingtang1,FANHongbo1,LIZhining1,ZHANGShuai2

(OrdnanceEngineeringCollege,Shijiazhuang050003,China)

Abstract:The total magnetic field detection anomaly include a single exception message and can not establish contact with the target through prior information in the inversion study of small ferromagnetic material target. A correlation imaging method based on magnetic gradient tensor data was put forward in this paper. Firstly, forward modeling data was obtained by using finite element method as measured magnetic gradient tensor data of ferromagnetic target. Then the subsurface space was divided into a 3D regular grid and each grid node was equivalent to a magnetic dipole. The cross correlation was calculated between the magnetic gradient tensor at the measurement surface and the observed data. The resultant correlation coefficients was used to describe equivalent magnetic dipole distribution in a probability sense. Finally, an iterative method was proposed to finish the transformation from probability value to actual physical parameter distribution. Theoretical analysis showed that this method could not only obtain the distribution of the small subsurface target, but also get the actual material parameter at different location.

Key words:magnetic gradient tensor; small subsurface target; correlation imaging; iterative calculation