小学几何知识结构化、经验化的教学策略研究

王　燕

(上海市徐汇区向阳小学，上海 200032)



小学几何知识结构化、经验化的教学策略研究

王燕

(上海市徐汇区向阳小学，上海 200032)

摘要：小学几何知识结构化、经验化是指个体形成几何认知结构的过程，它让个体在认知形式化的几何概念、几何方法，以及它们之间关系中，感悟出隐藏在活动情景背后的几何活动经验，并且能同时运用这两种知识展开几何认知活动。其意义是使学习者头脑中形成深水平理解的几何认知结构，减轻几何知识的记忆负担，缩小高级和低级几何知识的差距，提高班级几何学习的整体水平。文章围绕线段、射线、直线和角以及矩形和圆等几何知识结构化、经验化过程，对“梳理点状概念知识策略”“连接组块知识策略”“课内复习向课外延伸教学策略”三大策略进行分拆、论述和活动设计，为该领域的教学研究提供案例和经验。

关键词：小学几何；知识结构化；知识经验化；策略

传统小学几何知识复习的做法是：花最少时间，教师把阶段几何知识(概念、算法)简单地罗列出来，再让学生进行大量的习题训练，形成熟练运用知识和解题的技能，最终目的是取得优良成绩。本研究认为：几何复习既要重视双基的落实，更应重视几何二次认知中的知识关联性建构和整体性认知，要让每位学生梳理自己阶段知识学习的结构、方法和经验，进入对几何知识的深度理解(相对本学段的)，为后续几何知识学习做好充分储备(知识和能力)。为此，笔者尝试用系列活动让学生将自己分课时学得的几何知识进一步结构化、经验化，从而贯彻落实“四基四能”的新课标。

一、几何知识结构化、经验化的理性思考

1.几何知识结构化的意义

美国心理学家、教育学家布鲁纳曾在《教育过程》的引论中告诉我们：“无论什么课，务必要使学生理解这些科目的基本结构，这是使用知识、运用知识处理课外问题和事件，或者处理日后课堂训练中遇到的问题的最起码要求。迁移这一经典问题的核心，是结构的教授与学习，而不是单纯地对事实和技巧的掌握。”“如果前期的学习是为了使后期的学习变得更简单，那么必须有一张轮廓图，尽可能清晰地反映前期和后期遇到的事物之间的关系。”其中的“基本结构”“轮廓图”对几何学习来说，即指“几何认知结构”。它是几何知识结构与学生个体心理结构相互作用的产物，是学生在经历感知、思维想象、记忆、表象等几何认知活动中，在元认知的调控下把几何知识内化到头脑中，所形成的一个具有内部规律的整体结构。它主要由几何知识、几何经验和认知操作构成，所以，几何知识结构化就是指个体形成几何认知结构的过程。

个体良好的几何认知结构，必须经历自己对几何知识和几何经验的认知操作才能建构起来，很难想象不经历对单位课时的几何知识进行系统的结构化复习，就能自然而然地形成个体良好的几何认知结构。解题技能可以借助于习题训练，而几何认知结构是不能仅靠习题训练习得，尤其对于几何能力较差的学生而言，正如布鲁纳所指出的：“强调学科结构的优秀教学，对能力较差的学生比对那些有禀赋的学生而言，或许更为宝贵。”

单元几何知识结构化的益处主要体现在三个方面：首先，单位课时习得的几何知识是松散的，以点状分布的，对每一知识点有完整认知，但缺乏对系统中其他知识点的结构联系。从这点而论，可以说它还处于浅水平的习得。在复习中经过对几何知识点的概念与概念串珠成链，概念与方法、方法与方法组链成块，让学生看清概念间的、组块间的结构联系，用感知、推演、析取等认知操作组建几何知识整体结构，就会在学习者头脑中形成深水平理解的几何认知结构，如复习后理解“角是射线旋转而成，圆是线段旋转360°而成”。其次，深水平理解的认知结构有利于后期新知识的同化学习和顺应学习。如“线段旋转形成圆的思维结构”就有利于迁移建构“矩形旋转形成圆柱或半圆旋转形成球的思维结构”。同时，也有利于迁移组块知识解决一些复杂的问题。最后，复习中组织好几何知识既可以提高知识的利用效率，又能减轻几何知识的记忆负担，缩小高级和低级几何知识的差距，不因为知识的零散而模糊或遗忘，更能拓展几何认知记忆的容量。

2.几何知识经验化的意义

当代认知理论认为：人类通过认知活动所获得的知识，既包括语言、文字或符号等方式表现出来的明确知识之外，还存在一种非理性的活动经验、体会和感悟等默会知识。默会知识在整个学习活动中起着重要的作用。几何学习活动中也存在着明确知识和默会知识，如认识圆时，圆的定义、圆心、半径、直径等概念是明确知识，而在画圆活动中体会感悟出“圆心决定方位，半径决定圆的大小”这种经验体会，这就是默会知识。几何知识经验化就是让个体在建构认知形式化的几何概念、几何方法等明确知识的过程中，感悟出隐藏在活动情景背后的几何活动经验(默会知识)，并且能同时运用这两种知识展开几何认知活动。

几何知识经验化的目的是将几何的明确知识和默会知识融合起来，形成应用中的互动，让默会知识(经验)去支撑或加深对明确知识的理解，反之使明确知识在运用中产生更丰富的默会知识。因为默会知识是个体的几何实践经验、几何解题经验和几何思维经验，带有明显的个体特性和情景、条件特征。它能够起到对明确知识的活化作用，可以提高个体建构新知识的可能性，提高解决复杂几何问题的可能性。如：有了“圆心定位、半径定圆大小”的经验，就能提高“在矩形中作最大圆”的解题能力，“作对角线用矩形中心定位求作大圆圆心，再用矩形中心到长边的距离为半径”就能解答此题。

我们把班级视为学习型组织，几何知识经验化还有一个重要意义。根据野中郁次郎的组织学习理论可知，组织中的默会知识有一个公共化周期，最初发生在个体几何认知中，处于无语状态，是一种感悟或体验的隐性态。当这种感悟或体验成熟后，个体就会用隐喻的方式和外界交流，如果多种交流汇合就可能发展成一个语意表达的几何经验(显性态)。由于有了语言表达的可能，那么，初始的个体(小群体)感悟或体验就会以间接经验方式传播给组织的每一位人员，成为全班的公共几何默会知识。这将大大提高班级几何学习的整体水平，为后期的新知学习创造了条件。如：“射线绕端点旋转成角”的经验是“顺时针转角越转越大，逆时针转角越转越小”，这为以后建构“角的分类中的正角、负角概念，直角坐标系中讨论象限角、轴线角”创造了条件。

二、几何知识结构化、经验化的分析与构思

从一年级至四年级上半学期的几何知识教材内容编排的整体性出发，笔者整理出了下表，如表1所示：

表1　一年级～四年级教材几何知识整理表

随着年级升高，几何课时量逐渐增多，几何知识内容逐渐扩展，到四年级下学期学生初步认识了四种基本图形：线段、射线、直线和角，已开始认识由基本图形组成的日常生活中常见的图形：长方形、正方形、三角形、圆。在各种图形的学习中，学生既探究了图形的特征，又讨论了组成图形的各元素之间的关系、图形和图形间的关系，也积累了一系列的平面几何认识经验。问题是这种螺旋式认知安排，一个知识内容的学习周期跨度多的达三年，如线段的认识和角的认识，最少也要跨学期。所以，形成的几何知识结构中，很可能是碎片化的知识结构和无序的几何经验，对后期的几何知识学习会产生负面影响。笔者认为，本学期有必要让学生对已学几何知识进行梳理，一方面把点状的几何知识组建成块面的几何知识，另一方面寻找组块几何知识间的联系，使组块知识网络化。同时整理出点状学习时的经验，总结一些组块知识经验。把学习进程推向深度理解(情景化理解、条件化理解和结构化理解)，让几何知识和几何经验高度融合，形成个性化的理解。

第一，把线段、射线和直线结构化、经验化，用直线概念来统合线段和射线概念。初步得出“线段、射线都是直线的一部分”(见图1)：

图1　线段、射线和直线概念整合图

再把各自的端点数、可延长性、可度量性统一起来；最后把符号表示统一起来；用两个大写字母表示或一个小写字母表示。并且梳理出点和线(线段、射线、直线)之间关系的经验；直线和射线表示差异经验。

第二，将二次角的分类统一起来，把二年级静态学习的直角、锐角、钝角与四年级动态认识的平角、周角整合到一个图式情景中(见图2)，让学生在“射线绕端点的旋转”中，动态地归纳出：从特殊情况的0°(射线原形)旋转到90°(不包括90°)中间有无数个锐角，从90°(不包括90°)旋转到180°(不包括180°)中间有无数个钝角，当射线旋转回到原来位置时，形成了三个定值的角：直角、平角和周角。同时让学生体会出“旋转中角在变化，边的长短有无变化，角的变大变小和边的什么有关、什么无关”；体会出“量角、画角怎样用量角器，怎样读出度数”等经验。

图2　角分类的动态演示图

第三，将圆概念和矩形认识联系起来，让学生在作出“矩形中最大圆”的实践中，将最大圆半径和矩形短边一半联系上，将圆心和矩形中心联系上，体会出“圆心决定圆位置，半径决定圆面积大小”的经验，以及“矩形中画最大圆怎样定圆心、定半径”的经验等(如图3)。

图3　圆与矩形关系图

对上述三个知识组块又怎样联系起来织成网络呢？我们可以用射线旋转来串联第一和第二知识组块，让学生思考线段、射线和直线旋转，哪个能形成角？为什么？问题讨论完，两个组块的知识就黏合在一起了。我们可以旋转线段来串联圆和第一块知识，可以同样地问：线段、射线和直线中，谁能旋转成圆呢？为什么？这样就能把圆和第一块知识黏合起来，从而形成三大组块知识的内在整合。让学生经历这种几何知识整合过程，可以形成几何知识整体化组织的经验和感受，懂得知识是有联系的，运用时应系统化思考问题。

三、几何知识结构化、经验化的教学策略和学习设计

1.梳理点状概念知识的策略与活动设计

(1)阅读反思表格归纳策略

阅读反思表格归纳是指让学生对一个阶段学习的概念知识进行重温，可以是重读已学教材，可以翻阅本阶段的作业练习、错题本和测试卷，也可以查阅平时独立自学的辅导书，然后按照一定要求、范围，把一系列概念知识整理成一个结构组块的教学方法。

这一过程能使每位学生经历知识打包的过程，在反思中找到单点知识间的联系与区别，还能在整体中深度理解单点知识，这样就为个体知识的情景化、条件化、结构化奠定了基础，为活化个体应用知识创造了条件。

例如：在对直线、射线、线段反思归纳时，可以重温教材第一册第56～57页、第七册第79～80页，以及相应的作业练习或辅导材料，让学生按表格要求整理知识组块，然后迁移组块知识去解决问题(具体见表2、图4)，在解答问题后总结基本活动经验。

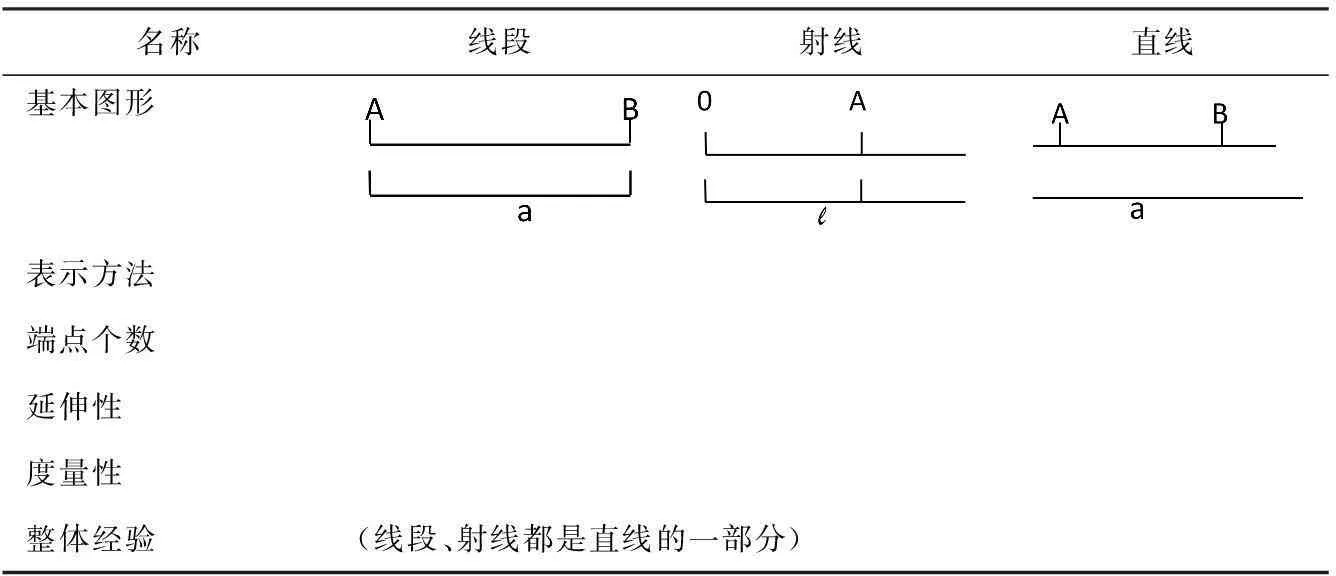
表2　线段、射线、直线知识整理表

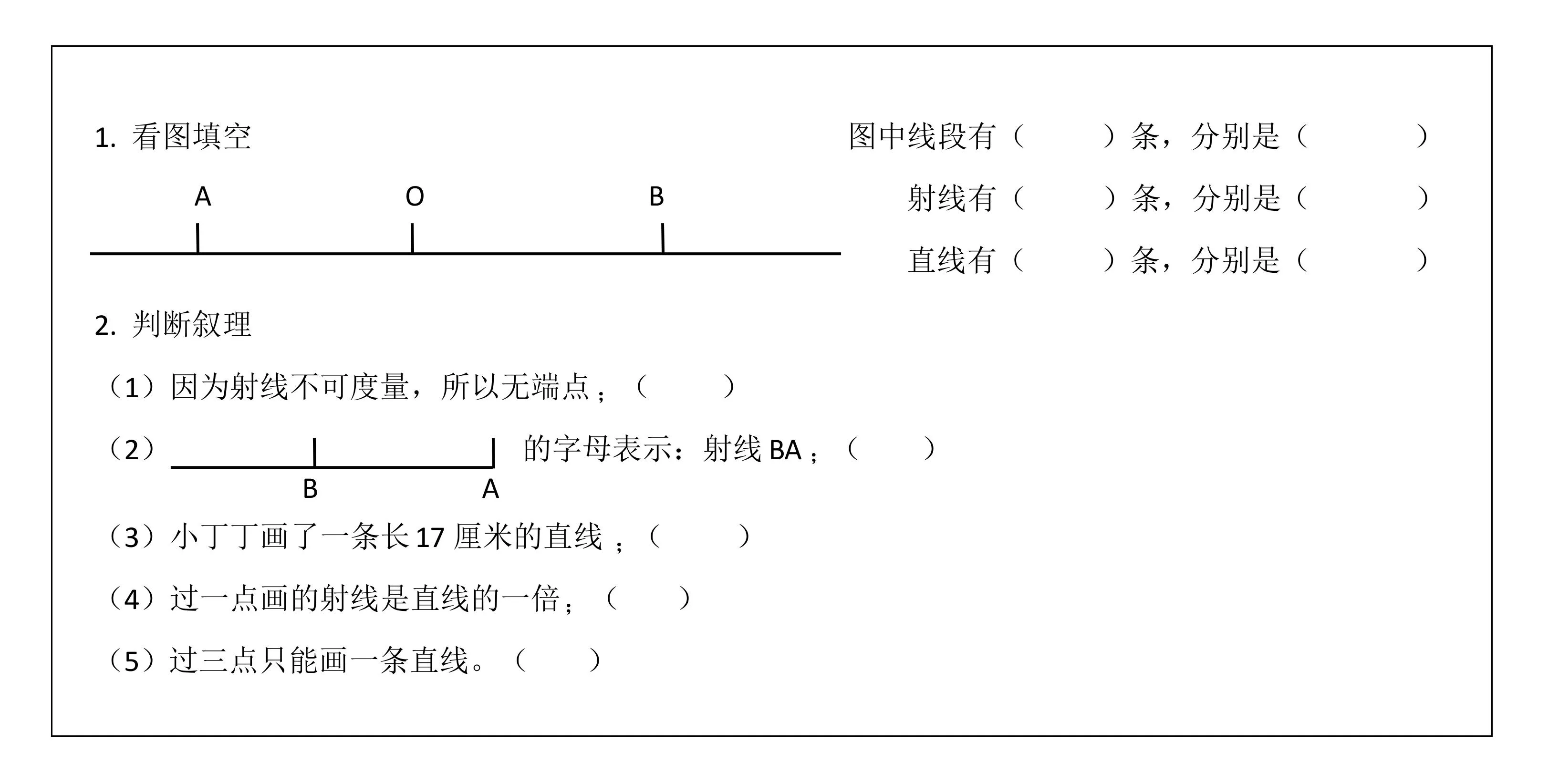
图4　线段、射线、直线知识反馈图

(2)视频解读图式化概括策略

视频解读图式化概况策略是教师设计动态连贯的、反映知识发生过程的视频课件，同时设计好观后需思考的问题串，让学生边观察图式的变化过程边思考问题，也可以边观察边开展小组讨论，学生在观察、思考、讨论中形成图式化的认知结构的一种教学方法。

这种方法能使学生在动态图象变化中，找出知识间的联系与区别，能把点状知识组建成知识网络图象，有利于记忆和储存，也有利于知识的整体迁移。

例如：在角的定义、分类、度量、关系的复习中，教师可以制作动态视频课件(如图2)，同时设计问题串(如图5)：

1.你见到一条什么线?正在做怎样的转动?(集体讨论)2.除了二年级用边来描述角的意义,你现在能用射线来描述角的意义吗?(小组讨论)3.按照从0°旋转到360°,你一共见到了哪几种角?次序是怎样的?(个体填空)4.如果把旋转出的角看成画角的过程,你认为画角有哪几步工作?怎样读出角的度数?(小组讨论)5.观看了此视频课件,你发现还有哪些关于角的知识没复习到?(小组讨论)

图5射线与角的关系的提问图

教师在完成观看视频后，提示学生可以用这样的图来记忆、储存角的知识，解题时可以想一想这个图是怎么告诉我们的。

(3)习题解答经验提取策略

习题解答经验提取策略是教师把需组合的知识、方法、经验设计到习题中，让学生在解题的过程中，把知识、经验、方法组合起来的一种教学方法。它既有组合知识的功能，还有提高解题能力的功能。

例如：复习由线段形成的图形时，我们可以设计前面如图3的习题：在边长为4厘米的正方形或长8厘米、宽4厘米的长方形中，画一个最大的圆。

教师在解题前布置解题后的讨论提纲：作画过程中，你是怎样确定圆心的？你又是怎么确定半径的？这样的解题用到前面哪些知识经验？

2.组块知识连接的策略与活动设计

(1)基本图形运动蜕变策略

基本图形运动蜕变策略是让学生操作基本图形的学具，使其在运动中产生生活中常见的图形(或形体)，从而发现基本图形和常见图形(或形体)之关系的一种联系性教学方法。

例如：课前让学生自制一件“打甩”，让学生拿着一头打圈甩开就能发现生活中存在的圆。然后总结出：握点是什么？另一端挂物怎样转动？“打甩”类似我们学过的线段，还是射线或直线呢？射线和直线能转出圆吗？思考完一系列问题后,学生自然而然地将线段和圆关联起来,从而也把基本图形和日常生活图形组织起来了。

(2)问题思辨质疑策略

问题思辨质疑策略是学生思考两个组块知识联系的问题，找出它们的联系点从而把知识整合起来的教学方法。

例如，复习中为了把“线段、射线、直线和角”两块知识联系起来，教师可以提出问题：线段、射线、直线中，哪些线旋转会产生角？为什么？学生根据角的动态定义进行说明后，就能将两种基本图形知识联结起来了。

3.课内复习向课外延伸策略

课内向课外延伸策略是一个将课堂集体复习活动中产生的班级集体公共知识转化成个人自有的认知结构的过程，就是课后学生参考课堂复习经历的知识认知系统，独立地用自己的方式呈现出来的一个过程。当然也可以课后，通过自组织形式来完成自己的知识复习构建。

本研究尝试该策略，让学生再经历公共知识私有化的过程，效果较为理想。好的学生能基本结构化地反馈出自己的几何知识，平时水平一般的学生能局部地反馈自己的几何知识。

四、反思几何知识结构化、经验化后的变化

当学生经历了几何知识结构化、经验化以后，在期终复习和期末测试中就有了不小的变化。

平时练习中解答“矩形和圆关联”的习题错误率较高，而在总复习和期末测试中正确率有了明显提高，说明学生能把圆的概念知识、圆的定位经验、圆的定大小经验和矩形的知识经验联系起来，获得了求解此类问题的思想方法。

图6　几何知识经验变化图a

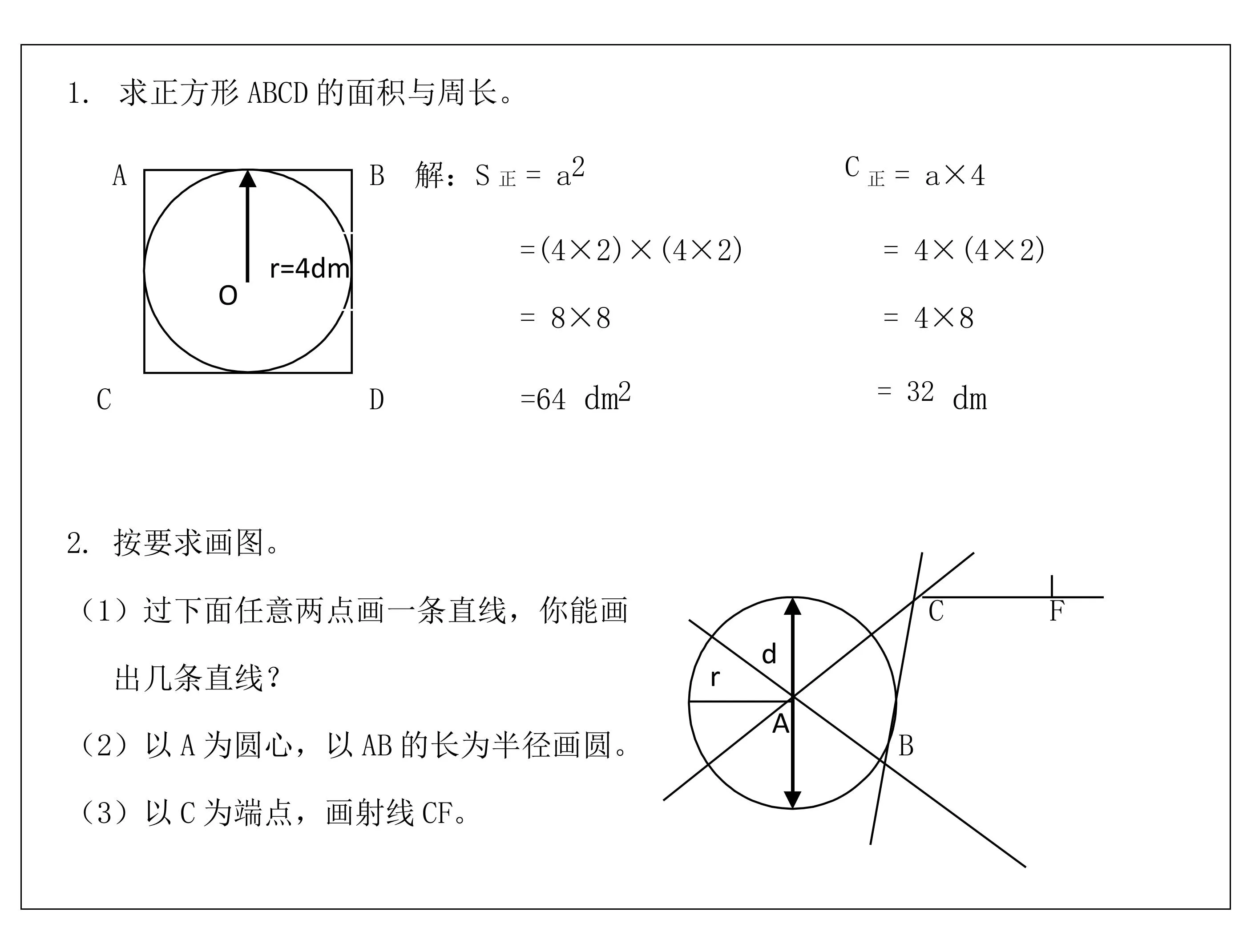
图7　几何知识经验变化图b

对比图6和图7中学生的解题过程，我们可以推断以下两方面的变化发展：

第一，从简单直接迁移运用知识变化发展到能用组块性的结构化知识来析题和解题。例如图6第2题，相当部分学生误把大圆半径当作小圆半径，说明学生缺乏跨知识链的推理能力，只能直接运用半径、直径概念关系来寻找答案，而不能作出“大圆半径为8厘米→大圆半径为正方形边长→小圆直径等于正方形边长就等长于大圆半径→所以小圆半径就是大圆半径的一半→是8÷2=4(厘米)的推理分析”。到了期末图7第1题，大部分学生在析题解题中都已经能够作出“组块性、结构化运用知识”的推理分析了。如“圆半径为4分米→圆的直径等于正方形边长→正方形周长就等于4个直径→所以正方形周长是4×2×4=32(分米)，正方形面积是(4×2)×(4×2)=64(平方分米)”。由此可得出经验性判断：学生的几何知识结构化程度提高了。

第二，知识和经验分离变化发展到知识和经验融合，并迁移运用。例如，图6第1题由于“圆心定位、半径定大小”的经验还没有和“长方形中最大圆的直径或半径”联系起来，所以误认为半径是宽的一半，那么直径就是长的一半。当期末两个经验已和长方形的对角线交点(中心)、内部大圆半径或直径相联系，就有了这样的迁移运用推理：“长方形内画最大圆→圆心在长方形的中心(对角线交点上)→最大圆的直径不能大于宽，否则会画出长方形， 所以最大圆直径就等于宽→用宽的一半做半径，以对角线交点为圆心就能画出长方形内最大圆”。可见期末50%以上学生能正确解答“矩形中画最大圆”的题目，证明学生把几何知识和几何活动经验融合的程度大大增加了。

还有在平时练习中，学生对一些概念填空和判断总是会产生这样或那样的错误，到总复习后，同类的概念题的错误率明显减少。说明通过概念结构化、经验化作业后，概念的清晰程度提高了，学生能在概念结构系统中用分析性思辨去解决问题，而不是单点知识学习后，用那种机械识记性的工具性思维来思考问题，如图8所示：

判断:1.当直角的两条边长度扩大2倍就成为一个平角。原(√)现(×)2.两条射线相加等于一条直线。原(√)现(×)3.线段比射线短,射线比直线短。原(√)现(×)4.钝角的一半一定是锐角。原(×)现(√)填空:1.一个圆周被分成180等份,每份所对的角是(原1°,现2°)。2.钟面上12时30分时,时针和分针所夹的较小的角是(原180°,现165°)。

图8几何概念认知变化图

从图8的判断中可以看出学生第三方面的变化：从“静止的经验知识概念迁移判定”变化发展到“用动态的知识概念链来推断命题的真伪”。如原来“线段比射线短，射线比直线短”判对时学生这样想：线段有两端点、不能延长；射线有一端点、可一边延长；而直线无端点、可两边延长。所以两边延长的比一边延长的肯定长。而经过复习后，把线段、射线、直线知识结构化、经验化了，他们从整体结构和经验出发来思考三者关系：线段有两端点可度量，所以相对射线、直线短，可是射线、直线都可以无限延长，又都不可以度量，要多长就能延长多长，所以是无法比较长短的。从中可见，学生的几何思维已经从“机械的、量上的性状推断”变化发展到“本质的、性状的、抽象的性状推断”。

《义务教育数学课程标准》提出：数学教学活动必须建立在学生的认知发展水平和已有的知识经验基础之上。苏霍姆林斯基曾说：“在人的心灵深处都有一种根深蒂固的需要，这就是希望自己是一个开拓者、研究者和探索者。而在儿童的精神世界中，这种需要特别强烈。”在复习阶段让学生自主地将几何知识结构化、经验化，无疑是满足学生学习意识发展需要、提升学生数学思维品质、利于学生提高数学素养的一种有效方式。正如学生课后谈到的感想：“通过这次的单元总结及整理，不但巩固了本单元的学习内容知识,使我对于这些图形的概念更清楚了，发现了这些几何知识间的联系，还使我单元测验的成绩有了明显的提升。”“我觉得这种学习的方法我很喜欢,以后在复习阶段我会试着这样整理知识。”我们的教学目标也正是如此。

参考文献：

[1]杰罗姆·布鲁纳.布鲁纳教育文化观[M].北京：首都师范大学出版社，2012.

[2]石中英.知识转型教育改革[M].北京：教育科学出版社，2001.

[3]冯忠良,伍新春.教育心理学[M].北京：人民教育出版社，2000.

[4]王燕.小学数学活动经验总结课的思考与探索[J].静安教育，2011,(7).

[5]沈思萱.数学概念图与小学数学教学[J].静安教育，2015,(8).

[6]朱丽丽，张景斌.中、美、俄三国几何课程的比较与分析[J].首都师范大学学报(社会科学版)，2002,(S1).

[7]廖运章.美国NRC数学素养观及其影响[J].外国中小学教育，2015,(2).

[8]张红.数学的结构性及其课程教学中的结构主义[J].宜春学院学报，2013,(3).

[9]李高慧.小学生数学活动经验的教学现状调查研究[D].西南大学硕士学位论文，2014.

[10] 刘兰英.小学数学课堂师生对话的特征分析[D].华东师范大学博士学位论文，2012.

[11] 江艳.浅谈积累数学经验促进思维发展的有效教学[J].新课程·小学，2012,(7).

[12] 陈卓芸.在七年级数学课堂教学中有效利用错误资源的实践研究[A].杏坛的呼唤——2015年度上海市基础教育教研员专业发展评选成果集，2015.

[13] 郁璐,英承智.初中数学高频错误的成因分析及对策研究[A].杏坛的呼唤——2015年度上海市基础教育教研员专业发展评选成果集，2015.

Elementary Geometry Knowledge Structured and Experience of Teaching Strategy Research

WANG Yan

(Shanghai Xiangyang Primary School of Xuhui District , Shanghai 200032)

Abstract:Elementary geometry structured experiential knowledge refers to the process of individual cognitive structure geometry, it makes the individual in cognitive formalized concept geometry, geometry method, and explicit knowledge based on the relationship between their respective activities, feeling out of hiding behind the activity scene geometry activity experience, and can also use these two kinds of knowledge on geometric cognitive activity. Its significance is to make learners form a deep level of understanding in the mind of the geometry of cognitive structure, lighten the burden of memory geometry knowledge, close the gap between superior and inferior geometry knowledge, improve the overall level of learning geometry class. In this paper, around a line segment, ray, linear and angle; rectangle and circle geometry knowledge structured experience process, such as the concept of “combing point of knowledge strategy”, “connection group pieces of knowledge strategy”, “the review to the extra-curricular activities teaching strategy” three major strategies are analyzed, and activity design, to provide the teaching and research in the field of cases and experience.

Key words:elementary, geometric, structured knowledge, experienced knowledge, strategy

作者简介：王燕，上海市人，上海市徐汇区向阳小学高级教师，主要从事小学数学研究。