地方高校转型趋势下概率论与数理统计课程教学改革探索与实践*1

2016-07-21丛玉华于梅菊

通化师范学院学报 2016年4期

关键词：连续型数理统计概率论

丛玉华，于梅菊，殷　烁

(通化师范学院数学学院，吉林通化 134002)

地方高校转型趋势下概率论与数理统计课程教学改革探索与实践*1

丛玉华，于梅菊，殷烁

(通化师范学院数学学院，吉林通化 134002)

摘要:文章在地方高校转型的新形势下，剖析了概率论与数理统计课程在应用型人才培养目标中的地位和作用，构建了合理的课程内容体系，结合丰富的教学实例，提出了类比教学、案例教学、问题式教学、翻转教学、探究式教学、多媒体辅助教学等多种教学改革方法，为了突出应用型人才的培养，克服教学内容的局限性，提出了在教学过程中引入新的科学研究成果的几点思考.

关键词:地方高校转型；概率论与数理统计；教学改革

党的十八大报告提出要加快发展现代职业教育，推动高等教育内涵式发展．十八届三中全会提出，要深化教育领域综合改革，加快现代职业教育体系建设，深化产教融合、校企合作，培养高素质劳动者和技能型人才．2014年，国务院发布了《关于加快发展现代职业技术教育的决定》也进一步指出采取试点推动和引领示范等方式，引导一批本科院校向应用技术型高校转型，重点举办本科职业教育．在这种地方高校的办学定位和培养目标转换的新形势下，概率论与数理统计课程作为一门应用型的课程，如何能够抓住机遇，突出应用技术型人才培养的目标，探索新的教学模式，是目前值得关注的问题．

1明确地位和作用，建立合理的课程内容体系

1.1概率论与数理统计课程在学校人才培养目标中的地位和作用

概率论与数理统计是研究随机现象统计规律的数学学科，是与实际联系密切，应用性较强的一门数学课程，它在统计分析、金融决策、保险精算和经济管理等领域都有着广泛的应用，特别是随着统计软件的普及，使其应用已经涵盖到社会生活的方方面面，它是目前数学与应用数学专业大学本科阶段乃至其他理工类专业的唯一一门随机数学的必修课．由于其应用的普遍性，为了突出学校应用型人才的培养目标，该课程的教学目的是使学生初步掌握处理随机现象的基本理论和基本方法，培养学生利用所学的概率统计方法分析和解决经济活动和实践中出现的随机问题，通过辅助开设统计软件的实验课，着重加强学生实践应用型能力的培养．

1.2建立合理的课程内容体系

地方高校承担着为所在区域经济社会发展培养高素质的应用型人才，提供教育、科技和文化支撑的重要职能．因此学校人才培养的目标一定要体现地方特色，立足于服务区域经济和当地社会的发展．在地方高校转型的新形势下，我校进一步明确了人才培养的目标：立足于长白山区域社会，面向吉林，辐射全国，为基础教育、地方经济建设和社会发展服务．为了适应学校人才培养目标的调整，突出应用技术型人才的培养，数学专业的概率论与数理统计Ⅱ课程从限选课变为目前的必修课、学位课；很多非数学专业增加了学时，2014年物理学专业、制药与食品专业，2015年数学与应用数学专业这门课分别增加了16学时．根据学时及学生解决实际问题的需要，在原有基础上增加教学内容，数学专业增加了次序统计量，非参数假设检验、多因子方差分析、多元回归分析、Excel在统计分析中的应用等内容；物理学专业、制药与食品专业增加了估计与检验等内容.同时，学院开设了概率论与数理统计通识公选课.

2教学方法和手段的改革

地方高校中很多专业开设概率论与数理统计这门课程，这门课程的内容较多，章节之间密切联系，各专业设定的学时不同，讲授内容的深度、广度也不同，为了提高教学效果，就需要打破传统的教学模式，根据不同的内容设置合理的教学方法与使用不同的教学手段.让学生既掌握知识又能锻炼思维能力，进而提高分析问题、解决问题的能力、培养创新能力.课程组在教学中针对不同内容主要采用了类比教学、案例教学、问题式教学、翻转教学、探究式教学、多媒体辅助教学.

2.1类比教学

“类比作为一种推理形式,在数学的发展中有着重要作用,恰当地运用类比可以有效地培养学生发现问题、提出问题、解决问题的能力.而有意识地将类比思想运用到课堂教学中去,能培养学生自觉运用类比方法去探索、发现,进而获取新知识,提高数学的创新能力”.

数学家开普勒说:“我珍视类比胜于任何别的东西，它是我最可信赖的教师”．拉普拉斯也曾说:“甚至在数学里，发现真理的主要工具也是归纳和类比”．因此，在教学过程中恰当运用类比方法于概念理解、定理的证明、问题求解，对提高学生学习效率具有重要意义．

在概率论与数理统计课程教学中，根据章节的内容，有多处适合类比教学.例如，书中用离散型随机变量去近似一个连续型随机变量．通常称“把连续的问题离散化”.通过离散化，可以把离散场合的许多概念和结论推广到连续的场合．学习一维离散型与连续型随机变量时，发现要把离散推广到连续，相应地要把对离散型随机变量分布列pi求和变成对连续型随机变量密度函数p(x)求积分．在离散型随机变量的基础上再研究连续型就容易得多．由此，把离散型和连续型随机变量的有关概念和计算式进行类比是很有意义的.如表1所示．

表1　一维离散型与连续型随机变量的类比

定理1若ξ是连续型随机变量，密度函数为p(x)．又f(x)是实变量x的函数且

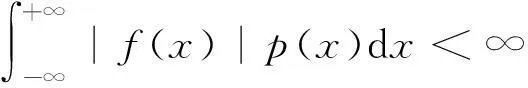
则有

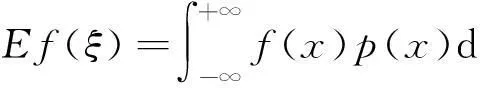
类比两个离散型随机变量函数的数学期望可以相应得到两个连续型随机变量函数的数学期望

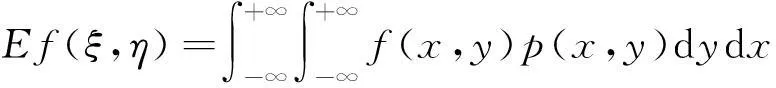
再例如，连续型随机变量数学期望性质E(ξ+η)=Eξ+Eη的证明，前面给出了离散型随机变量的数学期望的性质E(ξ+η)=Eξ+Eη的证明.根据二维离散型与连续型随机变量的元素类比表2，由离散型的证明过程，容易给出连续情况的证明.

表2　二维离散型与连续型随机变量的类比

这样可以通过类比给出结论的知识点还有很多，例如：一维、二维、维连续型随机变量的定义；边际分布列与边际分布密度的形式等等.进而引导学生“触类旁通”，猜结论，培养学生的创新能力.

2.2案例教学

案例教学有很多优点，首先，由于案例来源于实际，所以实践性强.其次选取恰当的案例可以激发学生的学习热情，引起学生的探知欲. 同时深刻理解理论在实际中是如何应用的，有助于提高学生分析问题、解决问题的能力.例如，讲大数定律时选用数学模型教材中的案例“报童的策略”：

“报童每天清晨从报社购进报纸零售，晚上将没有卖掉的报纸退回．设报纸每份的购进购价为b，零售价为a，退回价为c，应该自然地假设为a>b>c，这就是说，报童售出一份报纸赚a―b，退回一份赔b―c，报童每天如果购进的报纸太少，不够卖的，会少赚钱；如果购进太多，卖不完，将要赔钱．请你为报童筹划一下，他应如何确定每天购进报纸的数量，以获得最大的收入”．

这是一个非常实际的问题，因为需求量是随机变量，所以每天的收益也是随机变量，如何求收益的最大值？若以一段时间为期应该求平均每天收益最大，而这个平均值应该稳定于一天收益的数学期望，这时我们求当n为多少时，收益期望取最大值就可以了.为什么呢？我们引入今天要学的大数定律来说明原因.定理讲完后将这一问题利用实际数据圆满解决.

现在兼职或以后准备做营销的同学很多，涉及到利益话题，这是一个很多人感兴趣的问题．大大地提高了同学的学习热情，听课效果也会提升.在讲方差分析、回归分析等内容时都可以采用案例教学.

案例教学法课前要先选择案例．多年的教学经验告诉我们，选择案例既要典型又要贴近学生生活实际．讨论案例是案例教学过程的中心环节，教师应设法调动学生的主动性，引导学生围绕案例展开讨论，促使学生综合地运用所学知识主动发现问题、分析问题、解决问题，从而提高教学效果．

案例教学对教师提出了更高的要求，教师必须透彻理解案例所涉及的焦点问题，同时还必须把握问题所涉及的一系列理论基础，并由此得出结论．

2.3问题式教学

问题式教学就是在课堂上提出问题，启发、激励学生去“疑”去“问”，教学中以提出问题、分析问题、解决问题为线索，并把这一主线贯穿整个教学过程．目的在于掌握知识的同时培养学生的分析问题、解决问题的能力.例如，我们讲事件的独立性定义时，先给出了两个事件的独立性定义：若P(AB)=P(A)P(B)，则A,B独立.提出问题：如何定义n(n≥3)个事件的独立性呢？因为3是多之首，我们先考虑3个的情况，首先提出3个事件独立应该满足的条件，即两两独立且P(ABC)=P(A)P(B)P(C)，接着引导学生提出猜想：能不能由A,B,C两两相互独立，即P(AB)=P(A)P(B)，P(BC)=P(B)P(C)，P(AC)=P(A)P(C)，推出P(ABC)=P(A)P(B)P(C).或者由A,B,C 两两相互独立，推出P(ABC)=P(A)P(B)P(C)，通过引导同学列举反例说明上述猜测都不成立，因此3个事件的独立性应该同时满足上述的4个等式.这样同学对事件的独立性定义有了深刻的认识，n(n≥3)个事件的独立性定义也就随之给出了.

2.4翻转教学

在大学，课堂教学一般还是教师主讲的传统式教学方法，学生被动地汲取知识，目前这种方式的教学被越来越多的教学方法取代，翻转教学是以学生为主，自主学习，培养认知能力的一个重要手段.根据教学内容可以合理安排、设计翻转教学的章节.

例如，在假设检验的教学中，单个总体的参数假设检验与两个正态总体的参数假设检验，右侧检验与左侧检验，另一个参数已知与另一个参数未知，在分析问题时是同一种模式，教师可以讲授一种情况，另一种情况布置给学生，自己查阅资料，在课堂上让学生讲，让学生一起讨论，最后教师提点、小结得出结论. 既培养了学生自学能力，又能通过互动反应学生的理解程度，了解学生对已学知识的掌握情况.置信区间这一节的教学同样可以平行采用这样的方法.特别是单侧置信区间是书中没有提到的内容，与单侧检验相对应翻转教学，可以得到“事半功倍”的效果.

2.5探究式教学

概率论与数理统计的教学中涉及很多概念，学生在学习中容易混淆，在教学中必须辨析清楚，例如，对立与互不相容、独立与互不相容、随机变量不相关与随机变量相互独立、依概率收敛与弱收敛等等，教学中我们让同学推敲定义，反复举例，举反例，得出结论，进而加深对概念的理解．

还有我们的教学内容中很多量是有关系的，探究它们之间的关系，可以加深对知识的认识，例如，假设检验中犯第一类错误与第二类错误关系，假设检验与置信区间的关系、置信度与置信区间的关系等等，在课堂上我们可以通过图表，也可以通过推导让学生发现其中的关系，认清联系所在.

例如，在讲假设检验时我们提出问题：对于假设H0:μ=μ0,H1:μ≠μ0(1)如果在显著性水平0.05下拒绝原假设，在0.01下结论如何？(2)在显著性水平0.01下拒绝原假设，在0.05下结论如何？(3)在显著性水平0.05下接受原假设，在0.01下结论如何？(4)在显著性水平0.01下接受原假设，在0.05下结论如何？学生先讨论，也可以针对具体问题得出结论，最好的方式是通过图表得出结论.

2.6多媒体辅助教学

在概率论与数理统计课程教学中，涉及很多试验，如讲频率具有稳定性时涉及掷硬币试验，蒲丰投针问题时涉及投针试验，二项分布近似正态分布时涉及高尔顿钉板试验，正是因为对这些试验的研究，才有了后面的统计概率的定义、概率的性质、π的一种近似计算公式以及中心极限定理的特殊情形．如果只是给出试验结果，学生听起来比较“乏味”，因此我们在课堂上通过多媒体对于上述试验进行模拟，由于增强了直观性，同时可以多次变换试验参数或试验次数，显示不同的结果，可以让学生对相应问题有更深刻的理解，同时由于直观性强，大大地提高了学生的学习兴趣及求知欲，也培养了学生的创新意识.

在假设检验这一章的教学中，我们发现书中给的提法及例题、书后习题合起来都不够“面面俱到”,为了让学生更细致、全面地掌握这一部分知识，我们利用课件补全这部分内容，上课时提出并展示分析、求解过程，增大了课堂教学容量和效果，完善了知识内容体系.

概率论与数理统计课程教学中，为了更清楚地说明问题，往往离不开图、表的使用.利用多媒体展示特别是动态效果展示，更能加深学生对知识的理解和掌握.

3注重实践成果转化教学

3.1学生相关毕业论文的展示拓宽学生的知识结构

书本知识具有一定的局限性，章节内容侧重于理论，书后习题侧重于计算，应用类的题目很少，即使有应用题型也是“半成品”.为了能让学生学以致用，将理论应用到实践中去，拓宽学生的知识结构.在每一章的最后一节课我们都恰当地选取往届毕业论文中的相关问题，例如，概率论思想在疾病中的应用，条件数学期望的应用，特征函数的性质及应用，高考数学成绩对数学系三大基础课影响的统计分析，父母身高对子女身高影响的统计分析，数理统计在教育统计中的应用等，我们同学可以利用所学知识解决的问题．这样既能开阔学生的视野，也可以让学生效仿提出新的论文题目．

3.2讲解建模竞赛相关优秀论文优化学生的认知结构

每一年我们学校都组织学生参加吉林省或全国大学生数学建模竞赛，竞赛题目涉及到概率与统计知识的很多，在教学中我们对往届竞赛中涉及的本章节问题，利用多媒体进行展示，引导学生分析和建模，有时也带领学生课外小组课下讨论，题目如，彩票中的数学，零件的参数设计，葡萄酒的评价，施肥效果的分析等等．最后我们展示发表的优秀论文，提出我们模型中的失误与不足，极大地激起了学生的学习热情与动力，深化了学生的知识结构，同时也培养了学生分析问题、解决问题的能力，增强了学生参加竞赛取得优异成绩的的自信心.

3.3利用数学软件求解、解释相关问题，优化了处理问题的方法或手段

概率论与数理统计教学中有很多问题需要借助计算机处理以达到既省时又直观的教学效果，例如，我们讲二项分布近似泊松分布，我们又讲二项分布近似正态分布，在什么情况下近似程度最好？这就需要利用计算机作出曲线图，通过参数变化显示近似程度，进而提升了学生的认知结构，这个通常用Matlab软件包来解决.在方差分析、回归分析的教学中，由于数据量太大，在方法掌握之后利用板书或计算器求解都是不现实的，这时可以借助 Excel、Spss等软件解决问题.

3.4渗透学科新成果，探寻更合理更适合的教学模式

在二维离散型随机变量的教学中，判断两个随机变量是否独立，是解决问题的第一步，离散型随机变量相互独立的判别方法，教材上给了两种，一种是定义，利用联合分布函数等于各自分布函数的乘积；一种是利用定义给出的等价公式，对于任意的xi,yj有P(X=xi,Y=yj)=P(X=xi)·P(Y=yj).对于(X,Y)取值较少的联合分布律而言,利用等价公式判断较容易些,但对于(X,Y)取值较多的联合分布律而言,则计算量很大,造成了解题的繁冗;课本之外期刊上给出了另一种等价公式：

设(X,Y)是二维离散型随机变量,其联合分布律为

P(X=xi,Y=yj)=Pij,

i=1,2,…,m;j=1,2,…,n

矩阵P=(Pij)m×n称为联合概率矩阵.则X与Y相互独立的充分必要条件为rank(P)=1.

通过矩阵的初等变换，判断矩阵的秩是否为1,便可直接对随机变量的独立性作出相应的判断,使问题的研究得以简化.例如，已知二维离散型随机变量(X,Y)的联合分布律为

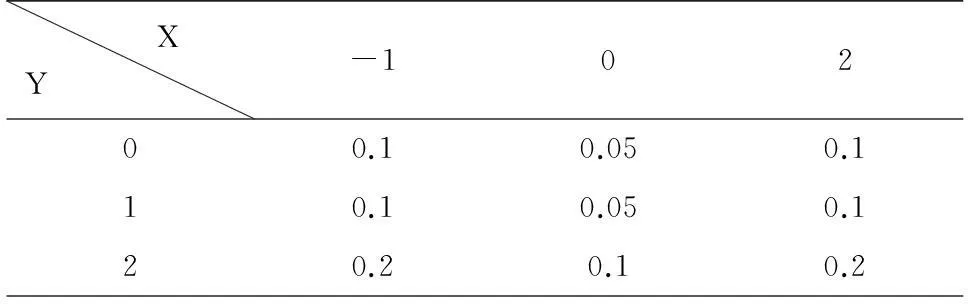
XY-10200.10.050.110.10.050.120.20.10.2

验证X与Y相互独立.易看出rank(P)=1，可知X与Y相互独立.

把握学科前沿，将科研成果及时引进教材，引进课堂，以科研成果促进教学，对锻炼学生的思维能力、综合分析能力、创新能力有重要意义.

总之，地方本科院校的转型发展为概率论与数理统计课程的发展带来了新的机遇和新的挑战，我们应该以服务区域经济为宗旨，培养真正适应市场需求的应用型人才为目标，加快概率论与数理统计的教学改革．本文从创新人才培养模式的角度，探讨了如何加强概率论与数理统计课程实践性和应用性的具体方法，希望能够为高校转型过程中其他课程的教学改革提供借鉴和参考.

参考文献：

[1]刘彦军.地方本科高校转型发展模式研究[J].中国高教研究,2015(10):82-86.

[2]张大良.把握“学校主体、地方主责”工作定位积极引导部分地方本科高校转型发展[J].中国高等教育,2015(10):23.

[3]汤克棣.浅谈新课程中类比教学[J].数学教学通讯,2011(12):25-27.

[4]罗小兵.类比建构在数学分析教学中的应用初探[J].荆州师范学院学报,2001,24(2):112-114.

[5]波利亚.数学与猜想[M].北京:科学出版社,2001.

[6]丛玉华.类比建构在概率论教学中的应用[J].通化师范学院学报,2008,29(4):86-88.

[7]姜启源,谢金星,叶俊.数学模型(第四版)[M].北京:高等教育出版社,2010.

[8]丛玉华,殷烁,袁志奇.离散型随机变量相互独立的判别方法[J].通化师范学院学报,2006,27(2):18 -20.

(责任编辑:陈衍峰)

DOI:10.13877/j.cnki.cn22-1284.2016.04.026

*收稿日期：2015-12-20