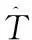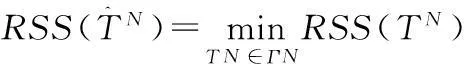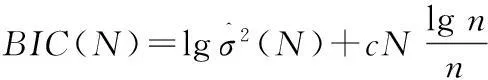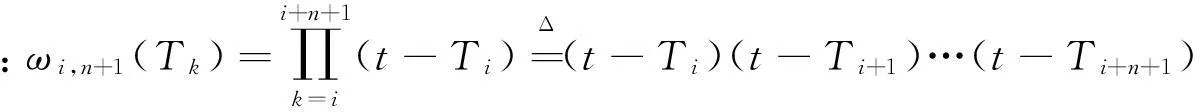相控阵雷达高采样率数据事后处理方法研究*

曹淑艳，陈琦

(1.中国人民解放军92941部队，辽宁 葫芦岛　125000； 2.北京理工大学 信息与电子学院，北京　100081)



探测跟踪技术

相控阵雷达高采样率数据事后处理方法研究*

曹淑艳1，陈琦2

(1.中国人民解放军92941部队，辽宁 葫芦岛125000； 2.北京理工大学 信息与电子学院，北京100081)

摘要：针对相控阵雷达高采样率数据，建立了雷达测量数据重采样的最优节点样条表示方法模型.为满足试验数据处理需求，进行拟合采样的同时用迭代方法将野值剔除，有效地降低了雷达测量误差。采用B样条作为数值逼近的基函数，可在全部数据范围内对测量数据进行拟合，达到提高处理精度的效果。通过仿真与实测数据的检验，验证方法的正确性和实用性。

关键词：相控阵雷达；B样条；拟合；数值逼近；重采样； 数据处理

0引言

外场试验中，相控阵雷达通常以20 BZ的频率来实时跟踪测量飞行器的轨迹，并采集和记录其测量数据，供事后分析处理。与实时输出20 BZ的雷达测量数据相比，事后用高采样率对雷达记录数据进行重采样能够获取更多的目标运动细节信息，提高数据处理精度，有利于对雷达测量误差进行修正和抑制。另外，雷达测量数据的采样时间和采样频率与其他测量设备很难统一，数据分析时也需要对雷达测量数据进行时间对齐，也就是对雷达测量数据拟合重新采样。

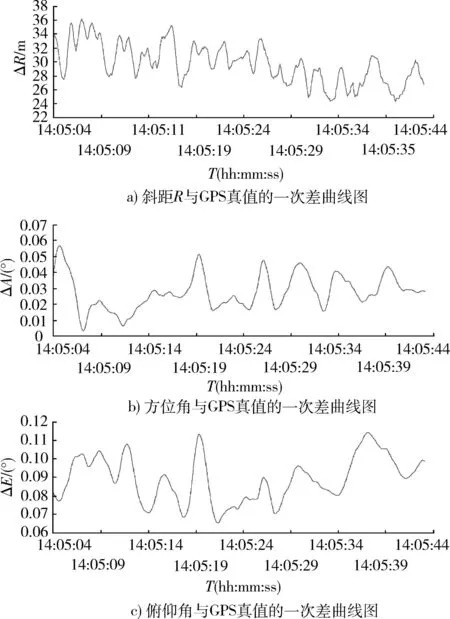
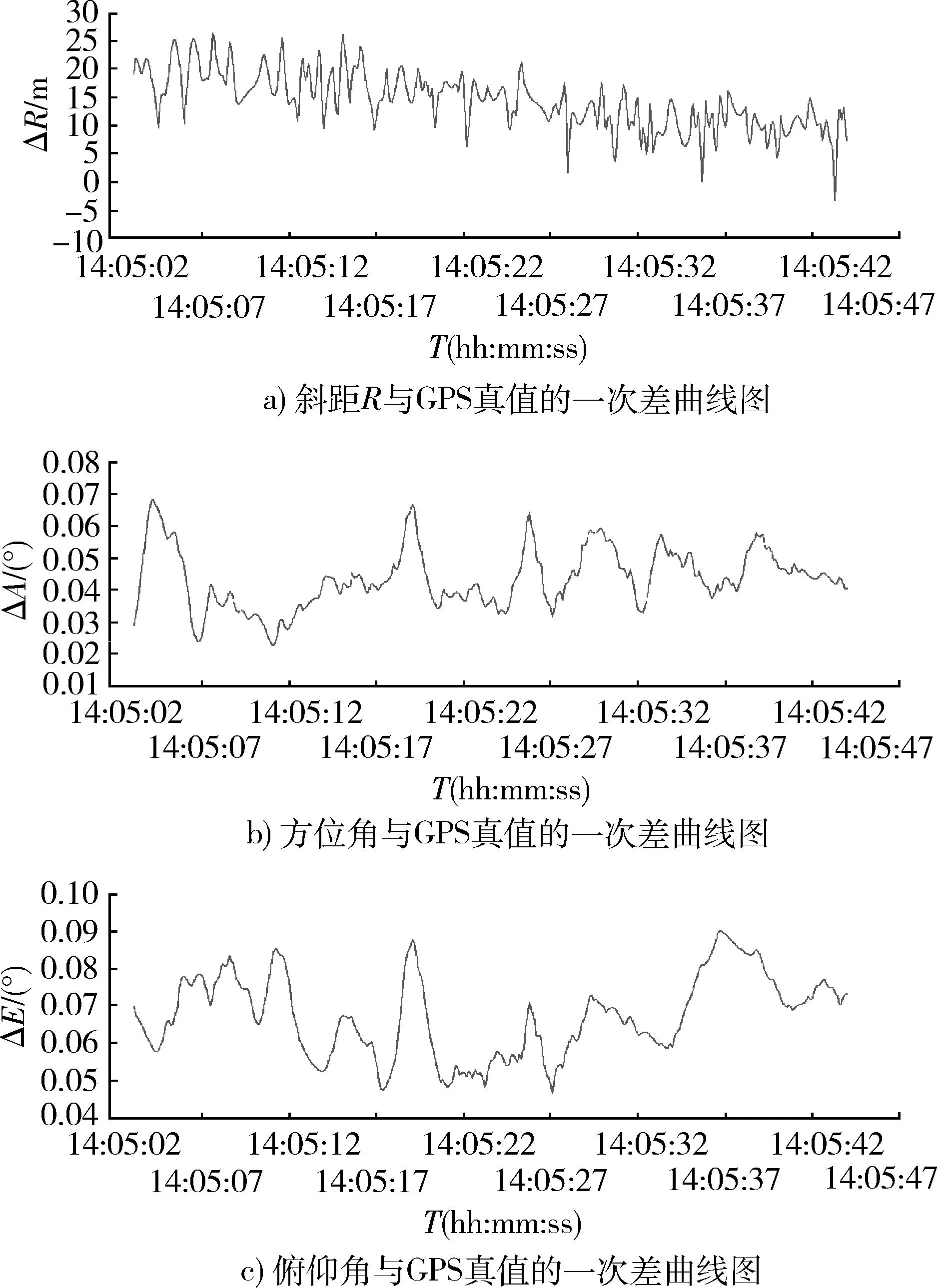
在对雷达跟踪飞行器测量数据处理时，目前多采用多项式拟合，但会带来较大截断误差[1-2]；若用分段多项式拟合，不仅段落划分比较费时，而且分段多项式衔接处出现拐点，严重影响了轨迹的光滑性与完整性。本文通过采用B样条拟合平滑方法，研究适当的平滑区间长度和多项式阶数，并采用B样条作为数值逼近的基函数，可在全部数据范围内对测量数据进行高精度拟合。通过对拟合的飞行器轨迹进行重采样仿真分析，并与GPS真值比对，表明该方法对雷达测量误差的抑制有较明显的效果。

1高采样率测量数据处理方法研究

针对常规测量数据处理中采用的最小二乘算法，对于含有修正残差的海上环境雷达测量数据，多项式的截断误差较大，由此导致处理的综合误差增大。而采用自由节点样条函数方法，通过合理的选择节点，可以有效地分离出测量数据中的误差，同时具有截断误差小的特点[3-5]。

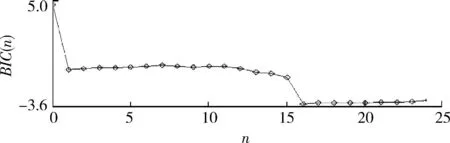
通过大量试验数据分析发现，影响样条函数处理效果的一个关键因素是节点的选取。首先，节点不能选择在噪声和修正残差较大的点上；其次，以含噪信号的特征点作为样条函数节点，能够达到较好精度。因此，在样条函数处理前，先对雷达测量数据作预处理，排除误差较大点的同时找出信号的主要特征点，以此作为样条函数节点的参考点。采用BIC准则对拟合残差与参数个数之间进行不同的权衡，以体现对残差与阶数二者重要性的不同侧重。同时还可对测量数据采用观察法，人工选取节点数，这一工程处理方法的特点是速度快，利于快速处理。本文基于对雷达测量数据拟合的重采样处理，有效地抑制了测量误差。

1.1基于B样条函数的最小二乘拟合法

样条函数是有限元理论中解决逼近问题的有效手段，它本身有诸多优良性[6]，因此，采用B样条作为数值逼近的基函数，可在全部数据范围内对测量数据进行高精度拟合，从而达到高精度平滑效果。

在最优节点样条拟合前，需要初步确定雷达测量数据所用的节点数。可采用BIC准则或观察法，确定样条拟合节点数。

考虑模型：y(t)=P(t)+e(t)其中y(t)为初始雷达测量的轨迹数据，P(t)为真实轨迹数据，e(t)为随机误差。

设y(t)具有N次样条多项式特征，并在m个时刻有采样数据{y(ti),i=1,2,…,m}，a≤ti≤b．可获得一个离散数据模型：

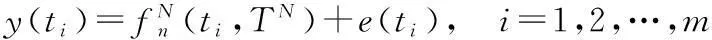
(1)

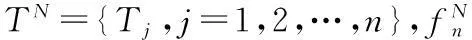
α=(α0,α1,α2,…,αn+N)T，

Y=(y(t1),y(t2),…,y(tm))T，

e=(e(t1),e(t2),…,e(tm))T，

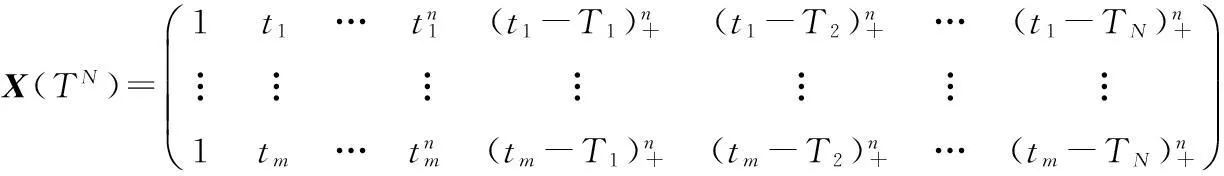
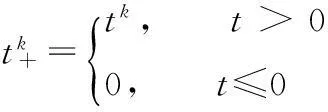
Y=X(TN)α+e.

(2)

模型(2)的参数估计可归为如下非线性优化问题: 即求参数α,TN，使得问题

(3)

式中：ΓN={TN=(T1,T2,…，TN):a

(4)

式中:RSS(TN)=‖H(TN)Y‖2=YTH(TN)Y， H(TN)=I-P(TN)，这里I是单位阵。

P(TN)=X(TN)[X(TN)TX(TN)]-1X(TN)T.

(5)

为定量地给出P(t)(信号)与ε(t)(误差)的分频界线，对下述BIC量进行分析：

(6)

由以上理论，可以构造出下面的分频算法：

Step 1： 给定N=L1，λ>0,δ>0及L2(L1≤L2)；

Step 2：IFN>L2GOTOStep 7；n=0，给定初始节点TN(0)(实际中，可由等距样条节点提供) ;

Step 3：计算▽RSS(τN(n)),τN(n);

Step 4：计算τN=τN(n)-λ▽RSS(τN(n))/‖▽RSS(τN(n))‖；

IFRSS(τN)>RSS(τN(n)),λ=λ/2, GOTO Step 4;

IFRSS(τN)

Step 6：RSS(N)=RSS(τN(n)), 令N=N+1，GOTO Step 2;

Step 7：计算BIC(N)，确定N=L1,…,L2,L中的BIC(N)的双极点N*，N**，即得到此段所对应的内节点数。算法中λ为收敛因子，δ为控制因子，L为最大样条节点数。

用不等距节点标准B样条拟合并返回每段的最小的BIC值对应的内节点数，算例对某一雷达跟踪某飞行器的一次试验数据计算结果如表1及图1所示(图中所示的值是无量纲的)，分析可得N*，N**分别为2和17。

图1　内节点数N及BIC(N)值图Fig.1　Inner node number N and BIC (N) value

1.2不等距节点样条拟合

采用四阶三次不等距B样条基，根据样条节点和样条阶数估计待拟合数据的样条表示系数[10]。

考虑t1,t2,…,tm时刻的轨迹的表示问题，

T-3

第i个四阶B样条函数为

表1　由BIC准则来确定的节点数N及BIC值

(7)

(8)

则数据可表示为

(9)

样条系数bj的估计值为

(10)

最优节点的确定步骤，具体算法如下：

Step 1：确定拟合样条的阶次；

Step 2: 确定拟合弹道的特征点；(允许为0)

Step 3：给定拟合样条节点的个数；(内节点允许为0)

Step 4: 给定初始节点；(实际中在各时间段内由等距样条节点提供)

若不满意，可修改step 2和step 3中的初始条件重新进行计算。

1.3样条节点和系数产生弹道参数

由得到的雷达测量飞行器初始轨迹参数的最优节点个数及最优节点序列，产生重采样的飞行器轨迹参数。

Step 1: 读取轨迹参数的节点；

Step 2: 对应于各个采样时刻t, 计算4阶3次不等距B样条及其一阶导数和二阶导数；

Step 3: 计算各个采样点的估计值；

Step 4: 按需要的采样率输出雷达数据。

2应用效果分析

应用本文的算法，对2次试验的雷达分别跟踪不同速度飞行器轨迹实测数据进行了仿真，并与GPS真值数据进行比对分析，如表2，3和图2，3所示。可以看出，通过对雷达测量数据采用B样条作为数值逼近的基函数进行拟合高采样率重采样处理[11-12]，有效地抑制了测量误差，轨迹更加光滑。

表2　跟踪某慢速目标仿真数据与GPS真值的比对结果

表3　跟踪某亚音速目标仿真数据与GPS真值的比对结果

图2　雷达测量数据与GPS一次差曲线图Fig.2　First difference between Radar measuring data and GPS value

图3　高采样率重采样与GPS数据的一次差比较图Fig.3　First difference between resampling at high-sampling data and GPS value

3结束语

针对相控阵雷达采集、记录飞行器轨迹测量数据的特性，研究的高采样率数据处理方法，并利用实测数据进行了验证[13-15]。通过对雷达跟踪的飞行器轨迹数据进行高采样仿真分析，并与GPS真值比对，对雷达测量误差的抑制有较为明显的效果。结果表明，利用高采样率所获得的目标运动细节信息，可提高数据处理精度，验证了所提出方法的有效性。

参考文献：

[1]罗海银．导弹航天测控通信技术词典[M].北京:国防工业出版社,2001.

LUO Hai-yin. Dictionary of Guided Missile、 Space、 Measure and Control、 Communication Technology[M].Beijing: National Defense Industry Press,2001.

[2]祝转民，杨宜康.样条函数最小二乘拟合的递推计算[J].中国空间科学技术，2002(1)：31-33.

ZHU Zhuan-min, YANG Yi-kang. Extrapolation Calculate of Spline Function Least Square Fitting Method [J].China Space Science Technology, 2002(1) ：31-33.

[3]王永德,王军.随机信号分析基础[M].北京：电子工业出版社，2009.

WANG Yong-de, WANG Jun. Analyze Foundation of Random Signal [M].Electronic Industry Press, 2009.

[4]刘利生，张玉祥.外弹道测量数据处理[M].北京：国防工业出版社，2002.

LIU li-sheng, ZHANG Yu-xiang. Data Processing of Exterior Ballistic Measurement [M].Beijing: National Defense Industry Press, 2002.

[5]杨位钦，顾岚.时间序列分析与动态数据建模[M].北京工业学院出版社，1987.

YANG Wei-qin, GU Lan. Analysis of Time Sequence and Dynamic Data Modeling [M].Beijing Industry College Press, 1987.

[6]崔锦泰.多元样条理论及其应用[M].西安：西安交通大学出版社，1985.

CUI Jin-tai.Multi- Spline Theory and Application [M].Xi’an:Xi′an Jiaotong University Press, 1985

[7]张金槐.线性模型参数估计及其改进[M].北京：国防科技大学出版社，1996.

ZHANG Jin-huai. Parameter Estimating of Linear Model and Ameliorating [M].National University of Defense Technology, 1996.

[8]王正明,易东云.测量数据建模与参数估计[M].长沙：国防科技大学出版社，1996.

WANG Zheng-ming, YI Dong-yun. Measure Data Modeling and Parameter Estimating [M].National University of Defense Technology, 1996.

[9]BAR-SHALOM Y, FORTMAN T E. Tracking and Data Associantion[M].New York: Academic Press,1988.

[10]王正明,易东云.弹道跟踪数据的校准与评估[M].长沙：国防科技大学出版社，1999.

WANG Zheng-ming, YI dong-yun.Calibrating and Evaluating on Trajectory Tracking Data[M].Beijing: National University of Defense Technology, 1999.

[11]蔡庆宇，薛毅.相控阵雷达数据处理及仿真技术[M].北京：国防工业出版社，1997.

CAI Qing-yu, XUE Yi.Data Processing of Phased-Array Instrumentation Radar and Emulation Technology[M]. Beijing: National Defense Industry Press,1997.

[12]刘利生，白堤.测量系统的系统误差主成分估计方法[J].宇航学报，1986(2)：1-9.

LIU Li-sheng,BAI Di.Principal Component Estimating Method of System Error for Measure System[J].Journal of Astronautics,1986(2):1-9.

[13]王省富.样条函数及其应用[M].西安：西北工业大学出版社，1989.

WANG Xing-fu. Spline Function and Application[M].Xi′an:XinBei Industry University Press, 1989.

[14]WANG Zheng-ming, ZHU Ju-bo. Reduced Parameter Model on Trajectory Tracking Data with Applications [J]. Science in China (Series E), 1999(2):190-199.

[15]张守信．外弹道测量与卫星轨道测量基础[M].北京:国防工业出版社,1992.

ZHANG Shou-xin. Base on Exterior Ballistic Measurement and Intersatellite Measurement [M]. Beijing: National Defense Industry Press, 1992.

Post-Processing Method for High-Sampling Rate Data of Phased Array Radar

CAO Shu-yan1，CHEN Qi2

(1.PLA，No.92941 Troop， Liaoning Huludao 125000,China;2.Beijing Institute of Technology,Information and Electronics college,Beijing 100081,China)

Abstract:Aiming at high-sampling data of phased array radar, an optimal node spline representation method is developed for radar measuring data resampling. To meet the needs of test data processing, the processed method could fit the samplings while eliminating the outliers, which may effectively reduce the radar measuring error. B-spline is employed as the basis function for numerical approximations, which makes the full-data-scale fixing of measuring data possible so that a high-precision may be achieved. The validity and practicability are verified.

Key words:phased array radar; B-spline; data fit; numerical approximations; resampling；data processing

*收稿日期：2015-09-09；修回日期：2015-12-21

作者简介：曹淑艳(1968-)，女，黑龙江密山人。高工，硕士，主要研究方向为数据处理与系统评估。

通信地址：125000辽宁葫芦岛市海滨南路1号E-mail：caoshuyan_ch@163.com

doi:10.3969/j.issn.1009-086x.2016.02.020

中图分类号：TN958.92；TP391.9

文献标志码：A

文章编号：1009-086X(2016)-02-0119-05