导弹装配角误差传播建模研究*

宁丹峰，陈万春，于江祥，张家杰，刘新建

(1．北京航空航天大学 宇航学院，北京　100083； 2．北京电子工程总体研究所，北京　100854；3. 北京航天新风机械设备有限责任公司，北京　100854)



导弹技术

导弹装配角误差传播建模研究*

宁丹峰1，陈万春1，于江祥2，张家杰3，刘新建3

(1．北京航空航天大学 宇航学院，北京100083； 2．北京电子工程总体研究所，北京100854；3. 北京航天新风机械设备有限责任公司，北京100854)

摘要：装配过程的误差建模是分析装配精度的重要手段之一。通过分析影响导弹装配结果的尺寸和形位精度、装夹定位精度，将装配误差源分为工装装夹精度和产品制造精度2类，不同形式的误差通过虚拟夹具的概念进行统一表达，基于误差流理论对导弹装配建立误差传播的状态空间模型，求出该过程的状态空间表达式，应用该模型对装配过程中的角误差进行分析。将分析得到的结果同蒙特卡罗仿真的结果进行比较，2种方法的相对误差小于3%，说明该方法可行。该方法的优势在于可分析复杂装配过程，还可对各工序装配效果进行观测及向后分析。

关键词：导弹装配；角误差；虚拟夹具；误差流；状态空间；蒙特卡罗仿真

0引言

防空反导导弹高速度、高加速度、高精度、采用复合力直接控制实现大变轨的特性，决定了动能杀伤拦截器总体结构设计的精度指标要高出三代防空导弹一个数量级以上，导引头与惯性测量装置之间的静态误差角，成为了保证控制系统精确制导需要重点关注的误差源之一。对于多舱段拦截弹的装配，这一问题由于误差的累积而变得更加明显。减小其装配角偏精度的意义在于提高产品的一致性、质量稳定性及系统可靠性，从而提高其整体性能，使其能效最大化。

多工序装配过程的建模与精度控制[1-2]已经成为了在工程和统计研究基础上新兴的研究领域，并在20世纪90年代取得了飞速发展。在早期研究中，MANTRIPARAGADA等遵循基准流动链(datum flow chain，DFC)的概念，将装配过程的各工序看成一系列离散事件，采用状态转换方程表示该离散动态系统，并引入控制理论对系统进行优化评价，从而改进装配特征以提高产品精度。威斯康星大学的CEGLAREK等人[3]提出了基于关键产品特性(key product characteristics，KPCs)的精度流分析模型，通过采用统一的广义虚拟夹具模型表征所有约束，该模型描述了关键产品特性和关键控制特性(key control characteristics，KCC)之间偏差的线性关系，为多工序复杂装配建模奠定基础。在这个基础上，JIN，CEGLAREK，HUANG等[4-8]提出以状态空间方程为模型对多工序的装配过程进行建模，采用向量公差来描述过程参数和产品质量特性的偏差。

本文仅针对拦截器的装配过程，建立其装配过程的状态空间模型，对装配角误差进行了研究。

1导弹装配角误差

导弹典型装配过程可简化为通过研究舱段装配特征进行。舱段的装配在工程中是非常普遍的，它按照装配方式可分为大型舱段的装配和中小型舱段的装配。其中，大型舱段装配的方式以焊接和铆接为主，如火箭等；而中小型舱段的装配方式多以螺栓连接为主，如中小型航天器、飞行器等。舱段装配的最重要的指标之一就是各舱段之间的角误差。本文以舱段装配为研究对象，主要关注不同舱段之间在装配后产生的角偏精度。

1.1角误差描述

这里用2个舱段的装配作为阐述，舱体1和舱体2是通过一面两孔的定位方式实现装配的，即通过2个舱段对接面实现轴向定位，通过在端面上180°分布的两定位销实现周向定位，并使用螺栓紧固。角偏精度为舱1局部坐标系和舱2局部坐标系对应坐标轴的夹角。舱体1和舱体2的局部坐标系分别建立在舱体1前端面和舱体2后端面上。如图1所示，舱体1的坐标系的X轴是其前端面的法线，Y轴是其前端面上两定位销孔中心的连线，再根据右手定则确定Z轴；舱体2坐标系的X轴是其后端面的法线，Y轴是其后端面两定位销孔中心的连线，再根据右手定则确定Z轴。α为两坐标系X轴之间的夹角，如图1右侧所示，即X1轴与X2轴夹角；β为两坐标系Y轴之间的夹角，如图1左侧所示，即Y1轴与Y2轴夹角；γ为两坐标系Z轴之间的夹角，如图1左侧所示，即Z1轴与Z2轴夹角。

图1　舱段装配后的角偏精度Fig.1　Angular Precision of Assembled Cabin

1.2基本假设

本文采用多工序刚体装配误差传播的状态空间模型来对其角偏精度进行分析，应用该方法的前提假设如下[9-11]：

(1) 刚体假设，即所有舱段被认为是刚体，因此，舱段偏移量可以由任意一参考点的偏移量描述；

(2) 刚性配合表面，配合面误差为各个配合面相对其名义位置的刚性偏离；

(3) 仅考虑装夹精度和舱段制造精度；

(4) 小误差假设，装夹精度和舱段制造精度相对舱段和装配尺寸精度的1/3。

2角误差传播

在每个工序上，通常包含2类误差源，夹具装夹精度和舱段制造精度。夹具装夹精度决定舱段定位精度。舱段制造精度是指舱段在制造过程中配合特征的尺寸精度和形位精度。制造精度包含多种类型，其描述形式也各不相同。为建立统一的误差流模型，必须将不同形式的误差统一建模。

文献[9]提出虚拟夹具(virtual fixture)的概念，认为舱段上施加一个虚拟的3-2-1定位夹具，舱段的任何误差都可以等效认为是虚拟夹具的定位点发生相应偏离，通过虚拟夹具的概念可以整合舱体制造误差于统一形式。

由于装配误差是微小变动，可以采用小位移旋量描述误差源，旋量表示法可以方便的转换为传递矩阵形式，从而通过状态空间坐标变换建立误差源与角误差之间的对应关系，以便于推导装配误差的累积与传播，实现在单一工位上建立误差流模型。

本文研究的舱段装配为一面两孔的定位方式，其虚拟夹具定位点布局如图2所示。第一基准面上的D1～D3定位点限制的是其X方向的平动、绕Y轴和Z轴的转动；D4和D5定位点限制的是其Y方向的平动和绕X轴的转动，相当于第二基准；D6定位点限制的是Z方向的平动，相当于第三基准。

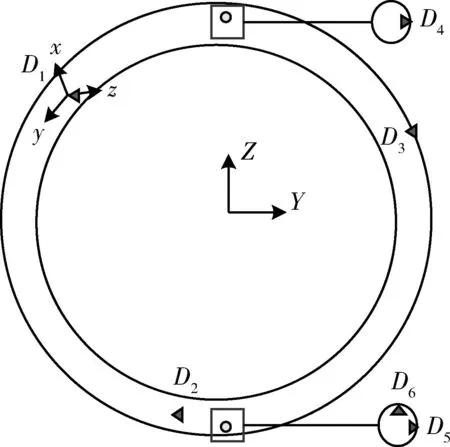
图2　一面两孔虚拟夹具定位点布局Fig.2　Locating points of 1-face-2-hole fixture scheme

定位点D1～D6的误差可以表示为

Δf=(Δx1,Δx2,Δx3,Δy1,Δy2,Δz1)T.

(1)

局部坐标系Oxyz的原点在D1处，定义与D1定位方向x正交的平面为第一基准面，该平面的法向量在全局坐标系下表示为x(nx,ny,nz)。在第一基准面内的局部坐标系的x和y轴可以由下式得到

x=nxi+nyj+nzk，

(2)

z=X×x=-nzj+nyk，

(3)

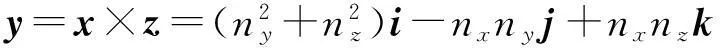
(4)

式中：x，y和z为局部坐标系的3三个坐标轴；而X，Y和Z是全局坐标系的3个坐标轴，也就是绝对坐标。

根据式(2)～(4)得到局部坐标系和全局坐标系的变换矩阵[9]：

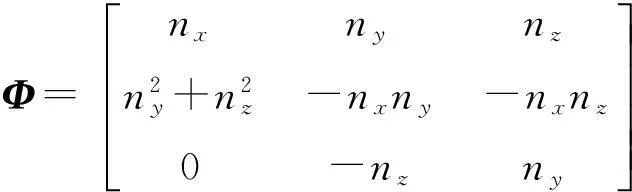
(5)

用ΔDr表示舱段上任意指定的参考点的偏移量，有

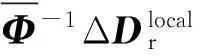
(6)

根据小位移旋量法，在局部坐标系下由夹具误差导致的ΔDr可以由公式(7)得到

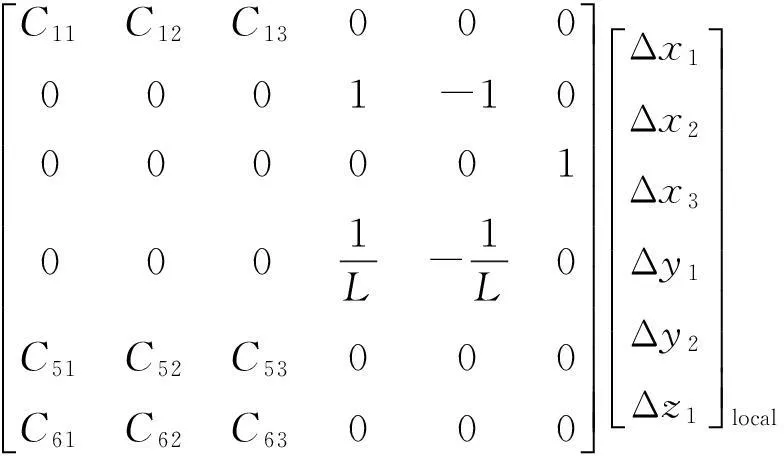
(7)

式中：，L为D4和D5在基准面上的距离；Cij为D1～D3对Δx，Δβ和Δγ的影响系数，具体数值由D1～D3选取的实际位置决定。令

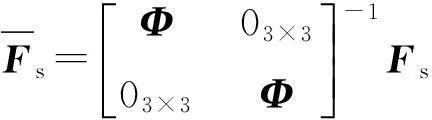
(8)

由式(6)～(8)可得

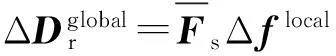
(9)

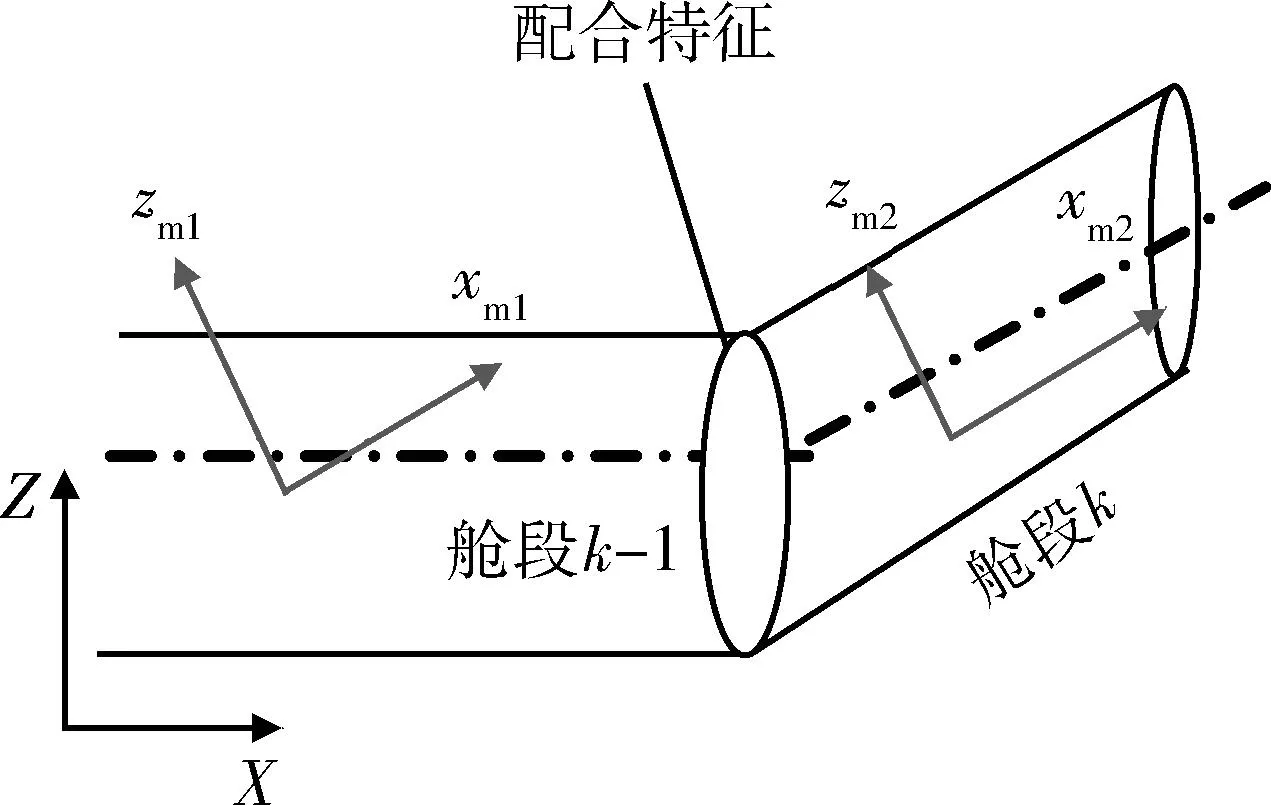
图3　配合特征在全局和局部坐标系的转换关系Fig.3　Transition between GCS and LCS of mating feature

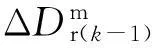
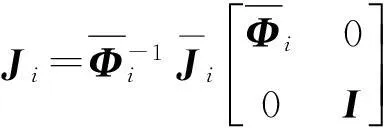
(10)

3装配角误差的状态空间建模

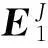
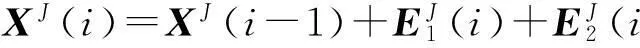
(11)

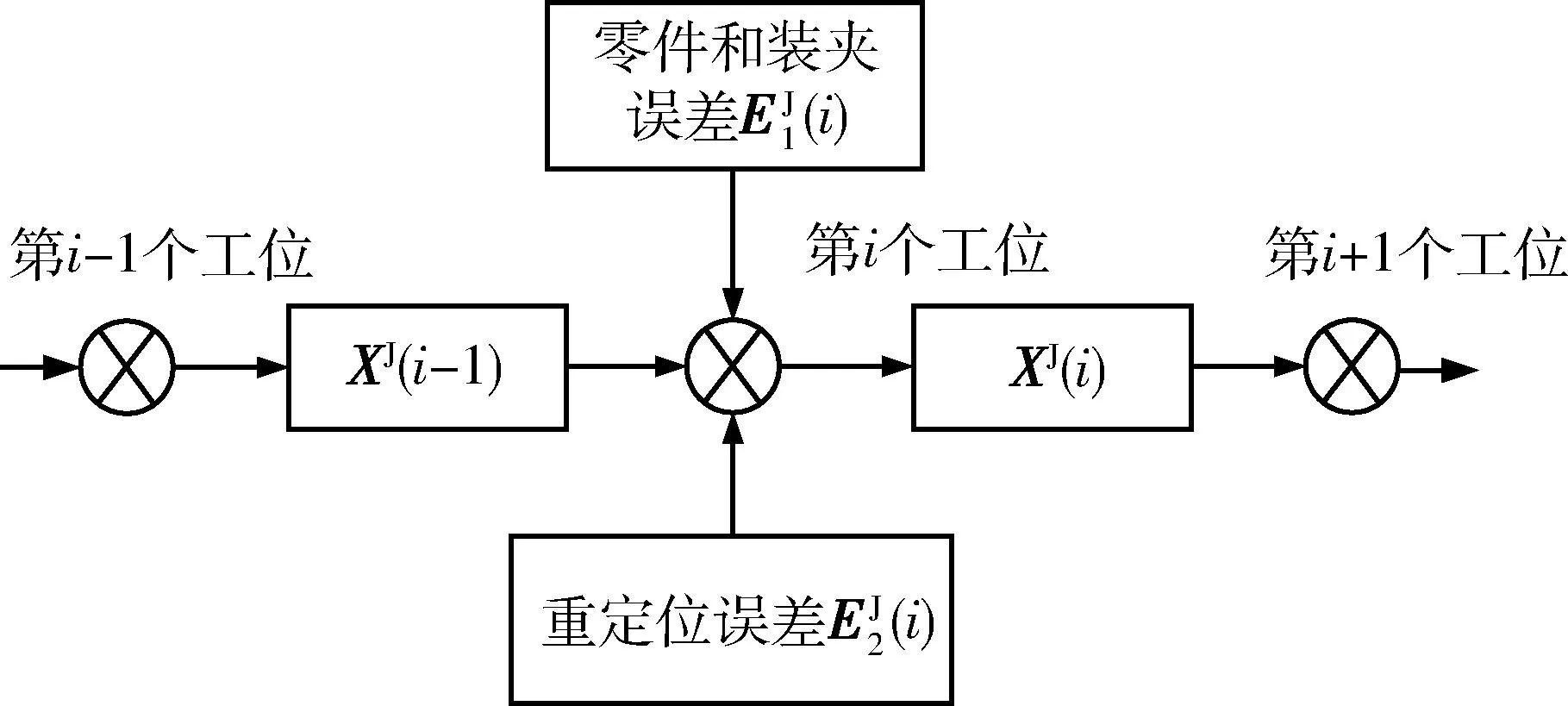
图4　舱体J在第i个工位上的累积偏差量Fig.4　Stream-of-variation model of single-station assembly

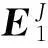
SHIU等人提出了在多工位装配过程中的重定位现象[13-14]。重定位就是在装配过程中不同工位之间的子装配体重新配置。例如，在第i个工位把舱体1和舱体2装配在一起，把这个子装配体转移到第i+1个工位上，如图5所示，主要是舱体2上的配合特征决定子装配体在第i+1个工位上位置，那么即使第i+1个工位上装夹十分准确，舱体1也会相对于其理想位置有偏差。这个由工位之间的转换引起的偏移量被定义为重定位误差。图中虚线表示舱体的理想位置，而实线表示的是其实际位置。

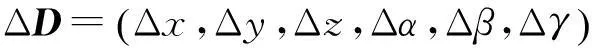
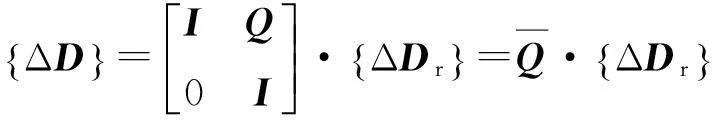
(12)

其中

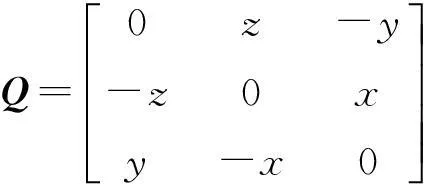
(13)

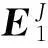
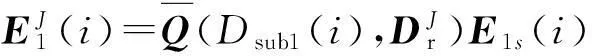
(14)

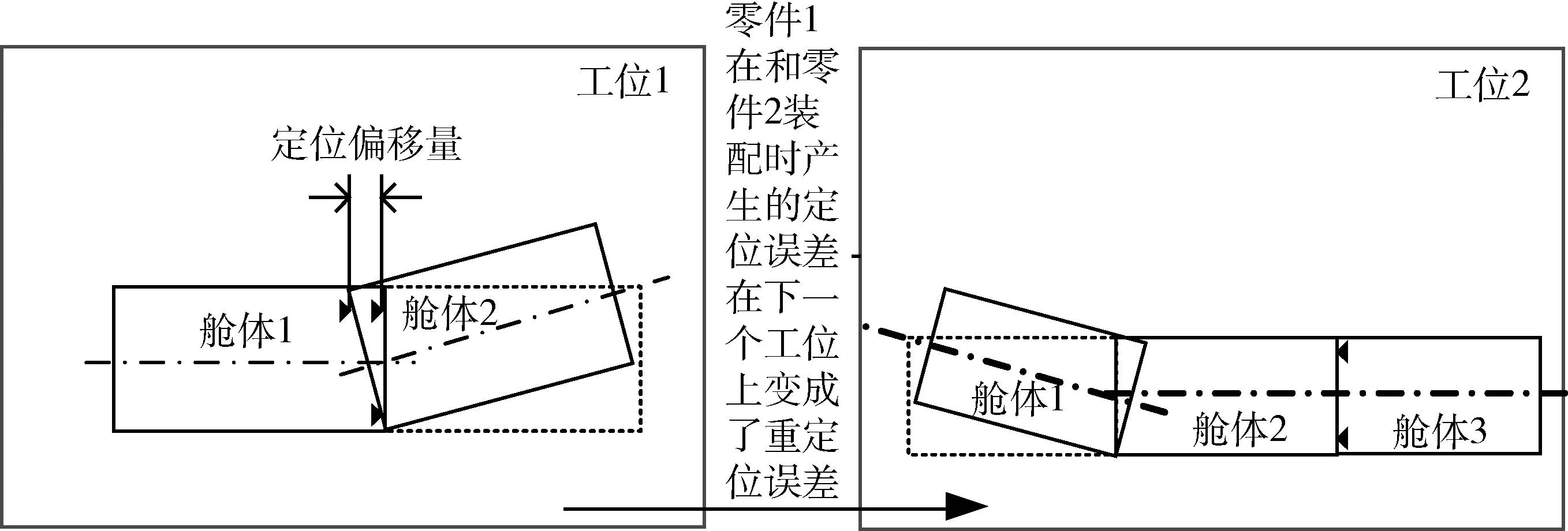
图5　重定位误差Fig.5　Re-orientation errors

式中：E1s(i)为参考点在子装配体s(i)上的偏移量。

多工序的装配过程的误差流如图6所示。所有向量定义如下：x(i)∈Rnt×1是累计的偏差量；U(i)∈Rm(i)×1是第i个工序贡献的装夹或舱段制造精度；Y(i)∈Rq(i)×1是第i个工序上的观测点偏移量的观测值；上标nt，m(i)和q(i)分别为3个向量维数；W(i)和V(i)是相互独立的噪声。

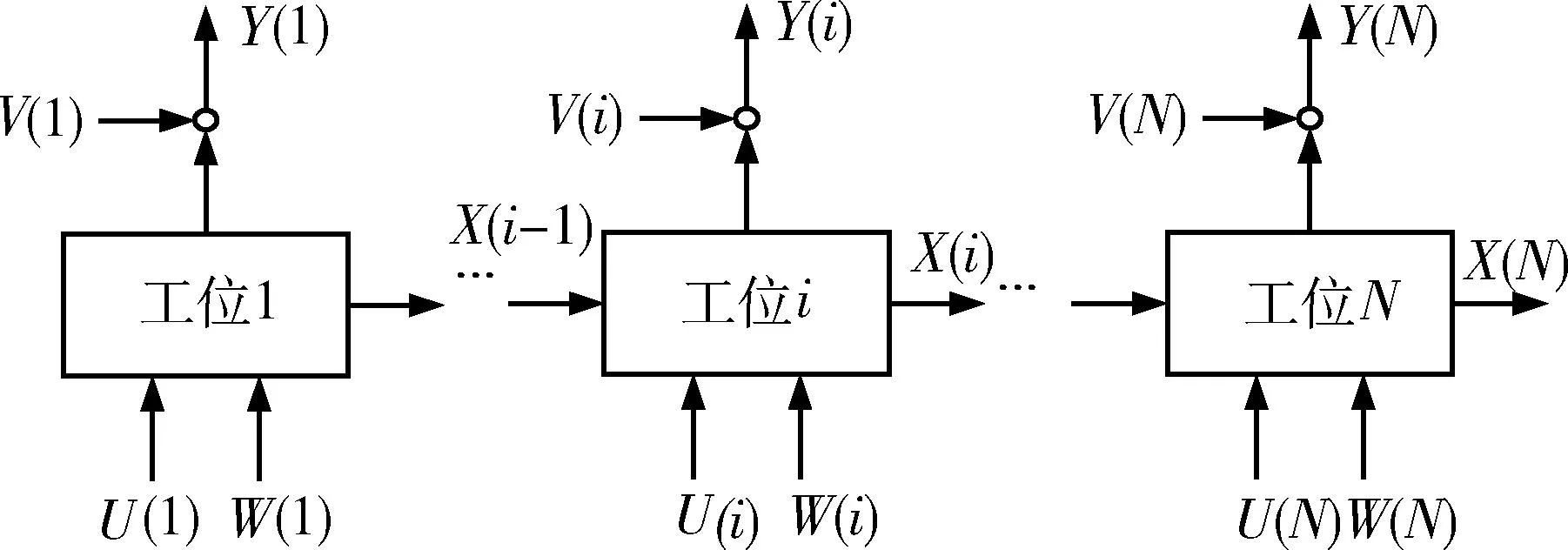
图6　多工序的装配过程Fig.6　Stream-of-variation model of N-station assembly

该装配过程中的误差流可以由以下方程表示：

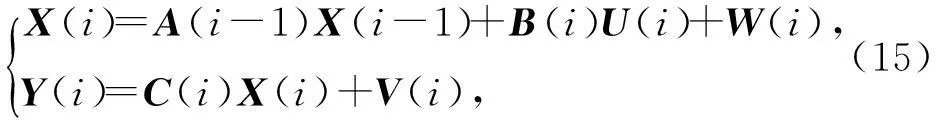
i=1,2,…,N.

动态矩阵A表征了在装配过程中的舱段在不同工序之间转换的重定位误差，决定于装配过程中的工序与工序之间的定位基准的变换。矩阵B是输入矩阵，它决定了虚拟夹具偏移量是怎样对舱段偏移量产生影响的。矩阵C包含了舱段上测量点的信息。

假设前面过程有ki-1个舱段参与装配，它们在第i-1个工序上组成了子装配体s(i)，然后按照装

配顺序在第i个工序上将ki-ki-1个舱段装配到s(i)上。在第i个工序结束后，有ki个舱段在新的子装配体上。因此，状态向量X(i)随着工序的变化不断更新。子装配体s(i)的系统向量方程为

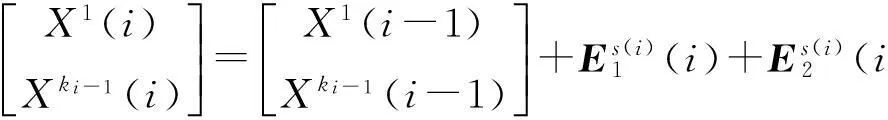
(16)

如果在子装配体s(i)中有ki-1个舱体，那么由子装配体装夹误差导致的所有参考点的偏移量可以表示为

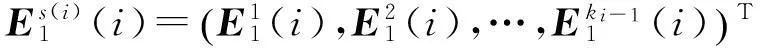
(17)

或表示为

(18)

根据研究的舱段模型可以得到：

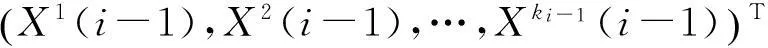
(19)

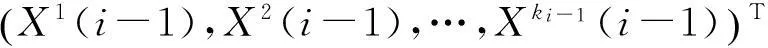
(20)

其中G(i)在文献[5]中给出了定义，其表达式为

G(i)=F(2)Q(i)S(i).

(21)

F(2)矩阵选择了偏移量的必要元素,S(i)是选择矩阵，它选择了在第i个工位上子装配体中有定位点的舱体。

这样，就可以得到状态方程：

(22)

(23)

(24)

A(i-1)受装配顺序的影响。在第一个工序上，前面工序的舱段偏移量为0，所以当i=1时，A(0)=06nt×6nt。F(x)(i)为维数变换矩阵,W0为第i个工位上误差累积的起始点，R(i-1)代表状态向量中引进重定位误差的元素,Λ(i)等在文献[5]中给出了详细介绍。

如果在第i个工序上的舱段J上取mJ个测量点，那么舱段J上的每个测量点的偏差量为

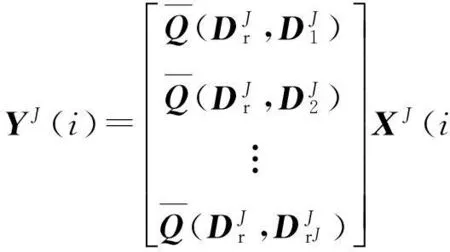
(25)

这样就可以得到每个舱段的所有测量点的偏移量表示，即为输出方程：

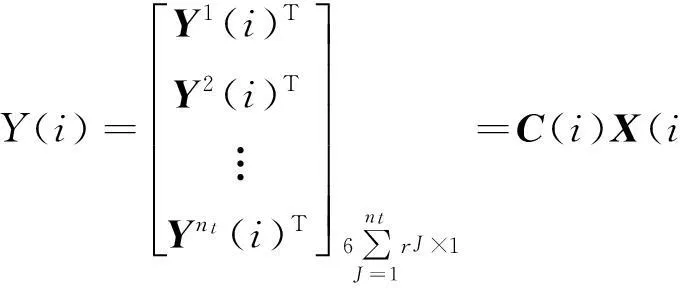
(26)

4模型仿真验证

设计一个三段舱段的装配过程用来验证该模型，装配过程总共分为3个工序，装配示意图及装配顺序如图7所示。

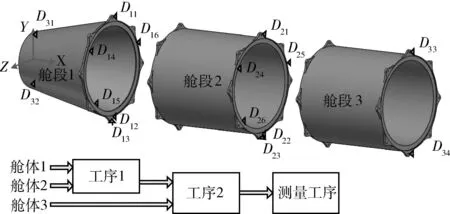
图7　验证实例Fig.7　Assembly example

其中误差源主要包括定位误差和配合特征面的误差。定位误差的平移偏移量假设服从正态分布N(0, 0.05)，舱段X方向的几何误差服从正态分布N(0, 0.1)，为了简化计算，使所有的局部坐标系的坐标轴与全局坐标系坐标轴平行。装配过程中有两对定位特征面，分别是舱体1，2和2，3的对接安装面，测量工序的定位误差很小，可以认为是0。其状态空间表达式可以写为

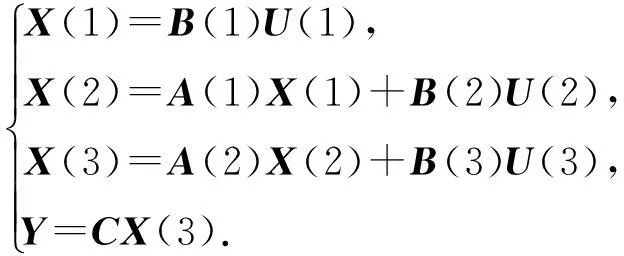
(27)

舱段定位点和测量定位点分别由表1和表2给出。

表1　零件定位点的坐标

表2　测量点的坐标

表3　用状态空间模型得到的参考点的偏移量

表4　用蒙特卡罗仿真得到的参考点的偏移量

由模型结构参数可知：

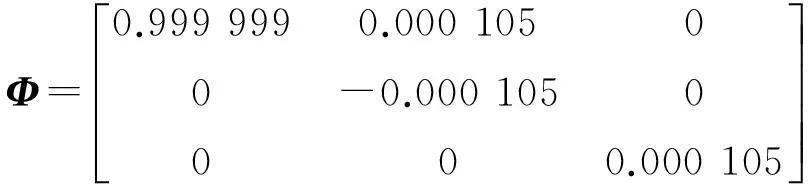
(28)

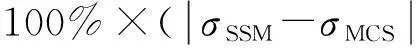
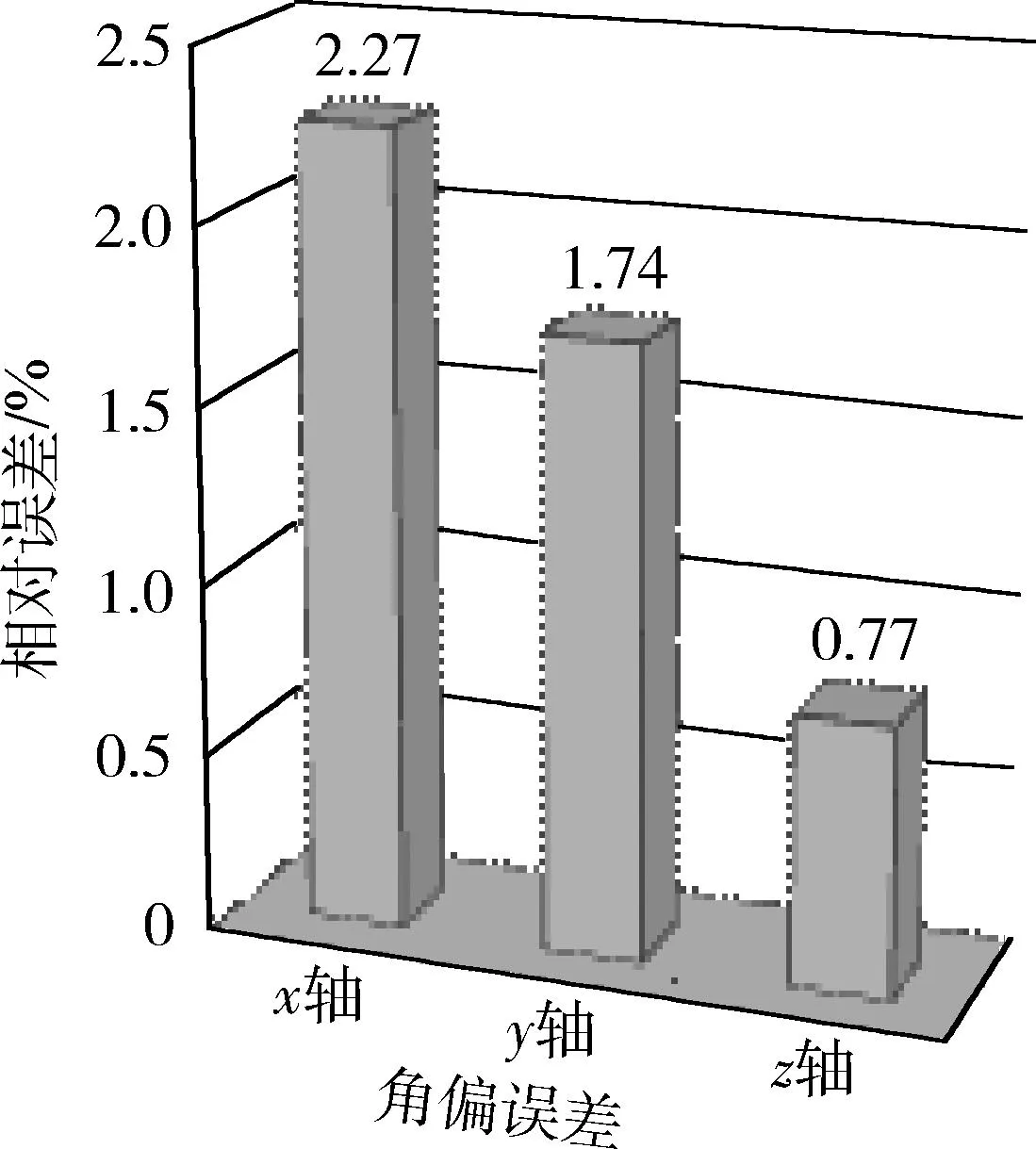
图8　角偏精度的相对误差Fig.8　Relative error of angular variation

另外，状态空间模型相比于蒙特卡罗仿真的一个优势就是计算效率的提升，这是由于蒙特卡罗仿真的大部分时间都用在了重复性的模型计算上。并且这个优势会随着模型复杂程度的提高而越来越明显。

5结束语

本文针对导弹的装配建立了其装配过程的角误差传播状态空间模型。该模型的建立得益于通过虚拟夹具的概念将不同形式的误差统一的表述成各个定位点的偏移量。该方法与传统的蒙特卡罗仿真相对误差小于3%，但该方法提升了计算效率，尤其是

在分析复杂度较高的装配过程；它更直观的表征了在装配过程中误差流动的趋势。该方法的优势在于它不仅可以分析复杂装配过程，还可以对各工序的装配效果进行观测从而进行向后分析。它不仅可以用于误差分析，还可以用于误差预测、设计评估、系统优化以及关键环节辨识。

参考文献：

[1]HUANG W, LIN J, KONG Z, et al. Stream-of-Variation ModelingⅡ: A Generic 3D Variation Model for Rigid Body Assembly in Multistation Station Assembly Processes [J]. Journal of Manufacturing Science and Engineering, 2007, 129：832-842.

[2]MANTRIPRAGADA, WHITNEY. Modeling and Controlling Variation in Mechanical Assemblies Using State Transition Models[C]∥Proc. Of 1998 IEEE International Conference on Robotics & Automation, Leuven, 1998：219-226.

[3]HUANG W, CEGLAREK D. Model Complexity Reduction in Stream of Variation for Compliant Sheet Metal Assembly [R]. 9th CIRP Int. Seminar on Computer Aided Tolerancing, Arizona, 2005.

[4]JIN J, SHI J. State Space Modeling of Sheet Metal Assembly for Dimensional Control [J]. Journal of Manufacturing Science and Engineering, 1999, 121: 756-762.

[5]SHI J. Stream of Variation Modeling and Analysis for Multistage Manufacturing Processes[R]. CRC Press, Boca Raton, 2006.

[6]DING Y, CEGLAREK D, SHI J. Design Evaluation of Multi-Station Manufacturing Processes by Using State Space Approach [J]. Journal of Mechanical Design, 2002, 124(4): 416-417.

[7]SOMAN. Functional Surface Characterization for Tolerance Analysis of Flexible Assemblies [D]. Brigham Young University, Provo, 1999.

[8]HUANG W, LIN J, BEZDECNY M, et al. Stream-of-Variation Modeling I: A Generic 3D Variation Model for Rigid Body Assembly in Single Station Assembly Processes [J]. Journal of Manufacturing Science and Engineering, 2004,129:821-831.

[9]HUANG W. Methodologies for Modeling and Analysis of Stream-of-Variation SOVA in Compliant and Rigid Assembly [D]. WI, University of Wisconsin-Madison, 2004.

[10]HUANG W, LIN J, KONG Z, et al. Stream-of-Variation Modeling—Part II: A Generic 3D Variation Model for Rigid Body Assembly in Multistation Assembly Processes [J].Journal of Manufacturing Science and Engineering, 2007(7): 11-12.

[11]HSIEH. Simulation and Optimization of Assembly Processes Involving Flexible Parts [J]. Manuf. Sci. Eng.,1996, 118(3):377-382.

[12]HUSSIAN T,YANG Z,POPOV A A,et al.A Method to Minimize stage-by-Stage Eccentricity Error in the Assembly of Axsymmetric Rigid Components[J].ASMEJ,Manuf.Sci.Eng.,2011,133(3):031014-031014-9.

[13]THOMAS. Rough Surfaces [M]. 2nd Edition. London: Imperial College Press, 1999:11-32.

[14]SHIU B, CEGLAREK D, SHI J. State Space Model of Multi-Stations Sheet Metal Assembly Modeling and Diagnostics [J]. NAMRI/SME, 1996, 120:199-204.

[15]LEONE F C, NOTTINGHAM R B, NELSON L S. The Folded Normal Distribution [J]. Technimetrics, 1961,3(4)：543-550.

Angular Deviation Analysis of Missile Assembly

NING Dan-feng1，CHEN Wan-chun1，YU Jiang-xiang2， ZHANG Jia-jie3，LIU Xin-jian3

(1．Astronautics college，Beijing University of Aeronautics and Astronautics，Beijing 100191，China;2. Beijing Institute of Electronic System Engineering，Beijing 100854，China;3.Beijing Aerospace New Wind Machinery Co., Ltd, Beijing 100854,China)

Abstract:Variation modeling is one of the most important tools for assembly precision analysis. Considering dimension and geometric variation, and part situation variation, the deviation source that affects assembly accuracy is clustered into two types: precision of geometric location and orientation, and precision of geometric form. These different types of variation or deviation are unified by virtual fixture. So a 3D rigid assembly state space modeling technique is developed for stream of variation analysis in multi-station processes. And a-missile-cabin-assembly process is analyzed in this model. It enhances the applicability in modeling complex assemblies. The developed methodology outperforms the current simulation based techniques in computation efficiency, not only in forward analysis of complex assembly systems, but it is also more powerful in backward analysis. The model is validated using Monte Carlo series Simulations.

Key words:missile assembly; angular deviation; virtual fixtures; stream of variation; state space; monte carloseries simulations

*收稿日期：2015-12-30；修回日期：2016-01-26

基金项目：有

作者简介：宁丹峰(1981-)，女，吉林通榆人。高工，博士，研究方向为导弹总体。

通信地址：100854北京市142信箱30分箱E-mail：lianghaolove999@163.com

doi:10.3969/j.issn.1009-086x.2016.02.008

中图分类号：TJ76;TP391.9

文献标志码：A

文章编号：1009-086X(2016)-02-0048-07