浮球式惯性平台动态积分滑模控制方法研究*

胡悦

(中国人民解放军92941部队，辽宁 葫芦岛　125000)



浮球式惯性平台动态积分滑模控制方法研究*

胡悦

(中国人民解放军92941部队，辽宁 葫芦岛125000)

摘要：浮球平台的内球是平台对惯性空间稳定的部件，其输出量的控制精度和快速响应能力相互制约。研究了平台稳定性与快速性的协调方法，采用了基于比例积分干扰观测器的动态积分滑模控制方法，并将其仿真实验结果与美国国防科技报告提出的LQR控制方法进行对比。实验结果表明，该方法可有效提高伺服回路稳态精度、改善系统动态性能。

关键词：浮球平台；快速响应；积分滑模；动态滑模；干扰观测器；前馈补偿

0引言

浮球式惯性稳定平台的概念最初由美国Draper实验室提出，用以解决弹道导弹的更换目标问题。浮球平台能够进行自动校准、对准，对弹体冲击、振动有良好隔离作用，隔热与温控效能高，温度场分布均匀，体积小，质量轻，能实现全姿态测量。因此，浮球平台与框架平台相比具有显著的优越性[1-2]。浮球平台早在1976年就在美国范登堡空军基地成功发射，经过多年研究实验，已经具有良好稳定的性能。由于该类平台制造难度大及所需对准标定技术的限制， 只有美国在“和平卫士”等战略导弹中装备

了该类平台。

20世纪八九十年代以来，我国陆续有学者展开了浮球平台国外文献翻译和研究工作，但由于当时国内精密制造领域水平制约，关于浮球平台的研究仅停留于理论研究阶段。近年来，精密制造业的发展为国内学者进行浮球平台实验研究奠定了良好基础，国内又陆续有学者开始了浮球平台的研究[3-4]，部分研究机构已经进入到实验研究阶段，但由于时间尚短，这些研究尚处于起步阶段，还未取得实质性成果。国外由于技术保密原因，关于浮球平台的公开文献非常稀少，时间也较为久远，但浮球平台对于惯性导航和武器系统发展具有重大意义，因此，国内对于浮球平台的研究仍是任重道远。

滑模控制理论经历了50余年发展，形成了一个相对独立的研究分支，国内外学者充实并发展了滑模控制理论[5-6]，部分先进理论已经用于解决惯性平台控制精度问题[7-8]。

浮球平台内球悬浮于外球壳内，受流体运动及电刷摩擦等影响，外球壳运动是流体阻力和刷摩擦力矩的根源。外球固定在载体上，在飞行过程中受到强烈的振动、冲击和摆动，从而迫使内球转动，相对惯性空间产生角位移。在未知干扰不明确的情况下，传统的控制方法难以实现高精度控制，且动态响应缓慢。为提高系统快速响应能力和控制精度，本文以文献[9]美国国防(AD)报告的数学模型为基础，提出基于内球单轴系统的滑模控制方法，设计比例积分干扰观测器和动态积分滑模控制器，最后将仿真实验结果与文献[9]的相关工作进行比较从而验证其有效性和优越性。

1问题描述及数学模型

1.1浮球式惯性稳定平台工作原理

浮球式惯性稳定平台的内外球体之间充满悬浮液，液压流体的浮力将内球运动与外球隔离。内球的基本结构可设想为1个立方体和6个球缺。惯性敏感元件(3个陀螺和3个加速度表)互相垂直放置于球缺内。液压支承垫在8个顶端，加矩阀的喷口在6个棱的中心，放置姿态带激励电路的槽开在6个棱上，液压涡轮泵放在球心[9]。图1是内球结构示意图[10]。

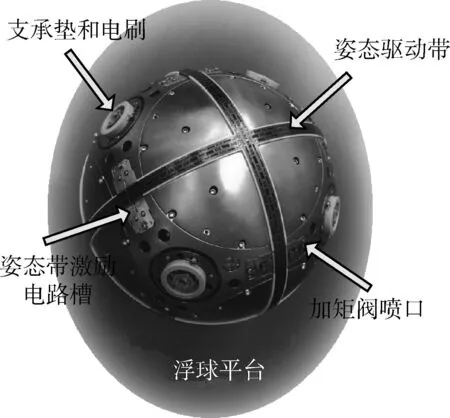
图1　浮球平台惯性参考球Fig.1　Inertially stabilized platforms

以单轴系统为例说明浮球平台的工作原理。平台外球固联于载体上，直接承受动力过载和各种角运动。外球运动给内球带来干扰力矩，使内球产生角运动，进一步扰动流体并产生了刷摩擦力矩造成内球受力更加复杂。在内球牵连角速度的影响下，敏感元件陀螺仪感受到这个角运动，并产生绕其输出轴的陀螺反作用力矩，使陀螺仪将绕其输出轴转动。陀螺仪输出信号经过处理输入力矩器(阀)，通过液压泵和液压力矩阀加矩，产生反馈力矩平衡外加干扰力矩，从而保证了在外干扰力矩作用下内球相对于x轴的角位置始终不变[11]。基于相同原理，由于三通道伺服回路共同工作，浮球平台在复杂干扰之下，其台体的角位置相对于惯性空间仍保持不变。内外球之间通过电刷传输数据和电源，通过姿态读出系统[12]提供外球相对惯性稳定内球的位置。

1.2内球单轴系统动态方程

内球的受力主要由2部分组成：有效力矩和干扰力矩，此外，还可能受到未知干扰du的作用。作用于内球的有效力矩Ta为阀门输出力矩与流体反应力矩之差；干扰力矩Td由刷力矩Tb、外壳旋转引起的流体阻滞力矩Tfd和不平衡力矩Tu组成。内球单轴系统的动力学方程为

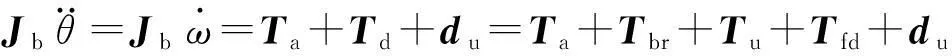
(1)

为叙述方便，认为有效力矩Ta为控制量，得到状态方程为

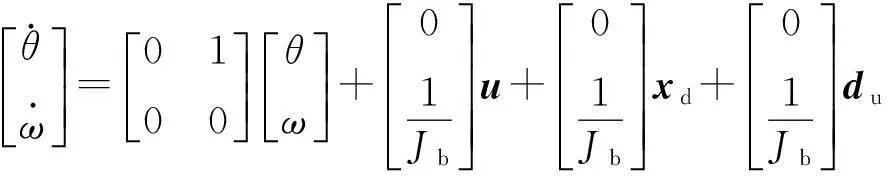
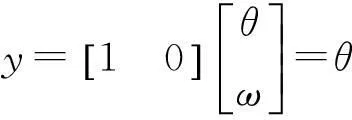
(2)

式中：θ，ω分别是内球绕自身转轴x轴旋转的角速度和角加速度，xd=Tb+Tu+Tfd。

2动态积分滑模控制器设计

浮球式惯性稳定平台内球作为对惯性空间稳定的部件，必须保证很高的控制精度和快速响应能力，同时尽量降低输出峰值。但是快速性与稳定性两者之间互相制约，这也是高精度惯性稳定平台需要解决的关键问题。滑模变结构控制是一类特殊的非线性控制，通过设计滑模面实现控制的不连续性。由于滑模面是可设计的且与对象参数及扰动无关，这使得滑模控制具有快速响应、对参数变化及扰动不敏感，无需系统在线辨识、物理实现简单等优点。该方法的缺点在于当状态轨迹到达滑模面后发生抖振。动态滑模控制[13]则通过设计新的切换函数或将常规滑模变结构控制中的切换函数s通过微分环节构成新的切换函数，该切换函数与系统控制的一阶或高阶导数有关，可将不连续项转移到控制的一阶或高阶导数中去，得到在时间上本质连续的动态滑模控制律，可有效地降低抖振。在滑模面的设计中引入积分项可以补偿模型的不确定性[6]，提高控制精度。本文提出的积分滑模控制方法就是将上述两种理论相互融合，以期达到显著提高控制精度和动态响应能力的要求。

考虑浮球平台内球单轴系统：

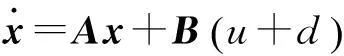
(3)

控制律的设计以状态量为基础，浮球平台上装载积分陀螺仪，因此只有θ是可测的。本文通过设计比例积分干扰观测器[14]获得干扰和状态的估值，能实现干扰的前馈补偿和基于状态反馈的控制器设计。观测器设计为如下形式：

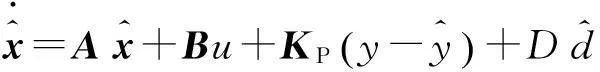
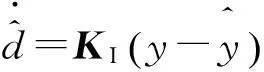
(4)

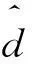
设计切换函数时，引入输出量的积分值，可有效降低输出量的稳态误差。定义切换函数为

s=Cxr+Du，

(5)

切换函数的一阶导数是：

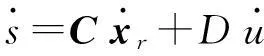
(6)

采用指数趋近率方法[15]可限制趋近运动的具体轨迹，改善趋近运动的动态品质。本文采用指数趋近率：

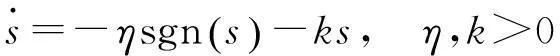
(7)

由式(6)和式(7)得到动态控制律为

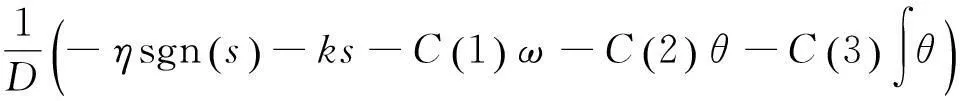
(8)

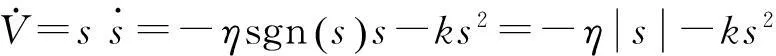
(9)

3仿真实验结果及分析

进行仿真实验时，将Tbr和Tu设置为常值干扰，Tfd与ωc有关，除此之外，令du为正弦扰动。因此，作用在内球上的干扰力矩如图2所示，图中实线是实际的干扰力矩。进行数值模拟时，选取参数

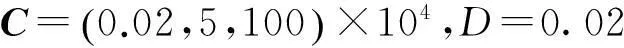
η=2，K=500.

由观测器获得的干扰力矩估计值如图中虚线所示。估计值趋近真值所需时间约为0.05 s，实时估计的延时约为0.03 s，同一时刻力矩差值约为0.05×10-3N·m。将有效力矩Ta设定为仿真实验的控制量，控制器输出力矩如图3所示，峰值约为9.4×10-3N·m，峰值时间约为0.01 s。从图中可以看出，控制力矩呈现近似于正弦的振荡，这是由于作用在内球上的干扰du是正弦干扰。

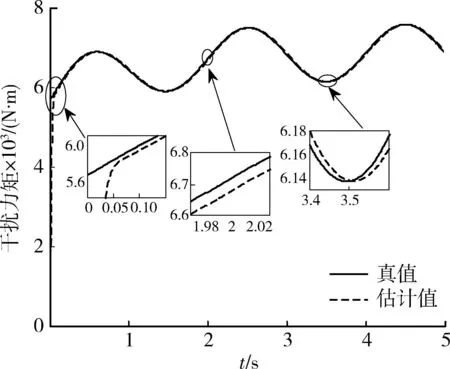
图2　干扰力矩Fig.2　Disturb torque

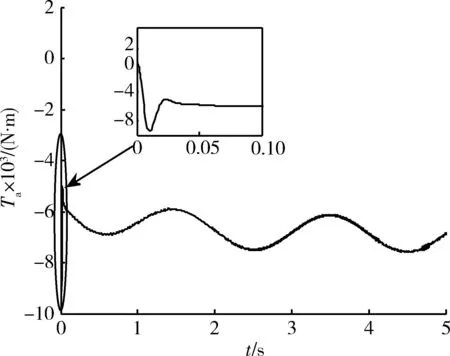
图3　控制力矩TaFig.3　Control torque

内球在干扰力矩和控制力矩的共同作用下产生角运动。本文就动态积分滑模控制方法设计的控制器与AD报告给出的LQR控制器进行了全面对比，仿真时对两者施加的干扰力矩完全相同。图4a),b)分别是AD报告和本文仿真结果的内球转动角度响应曲线，从图中可以看出，AD报告和本文的仿真实验结果均可将球体在有限时间内稳定到一定误差范围内。对于浮球平台来说，快速响应能力和较高的稳态精度是至关重要的，为详尽说明上述两点问题，图5分别就图4中的局部区域r1和r2作放大对比处理。

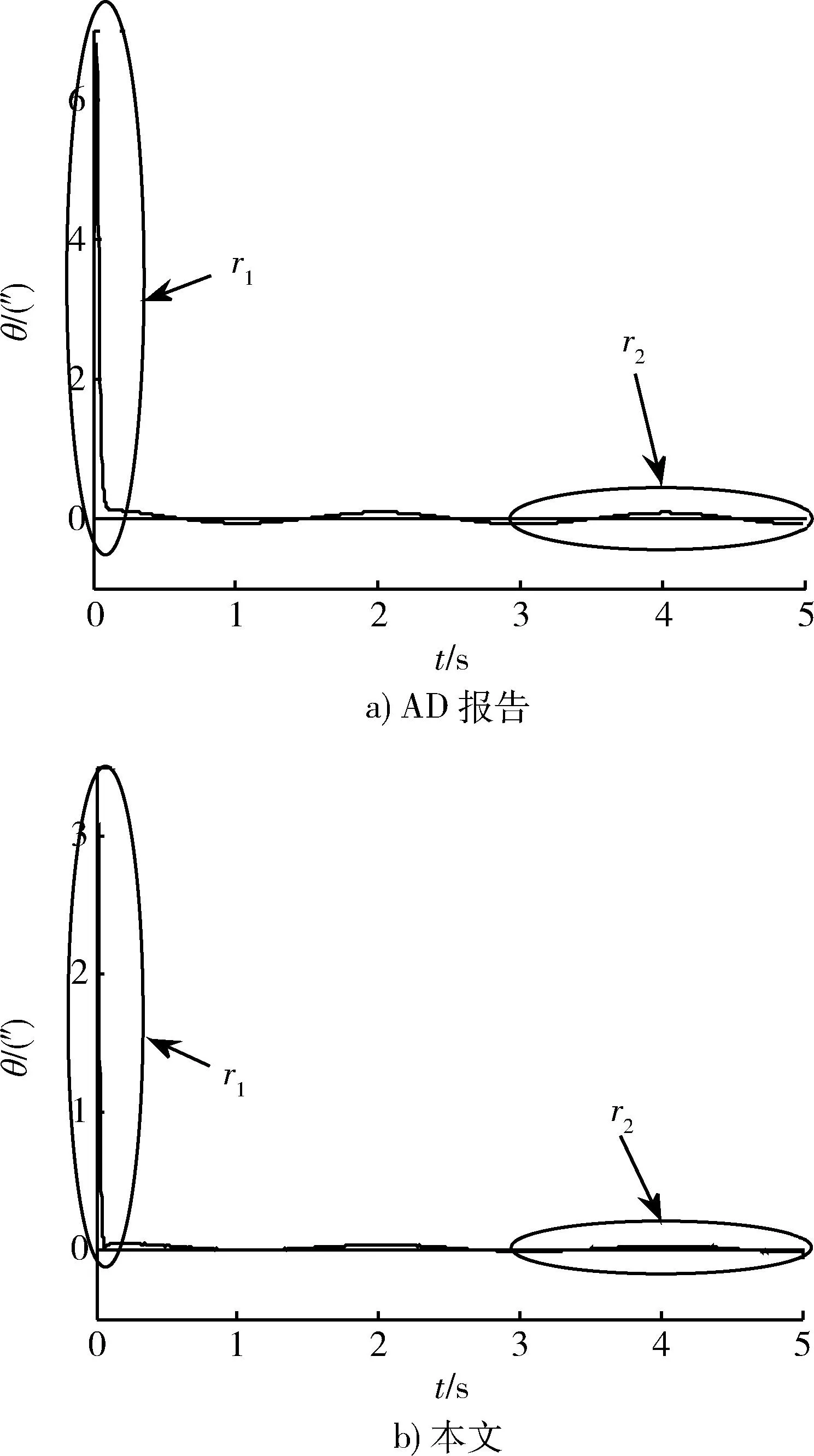
图4　内球转动角度对比图Fig.4　Rotation angle of the endosphere

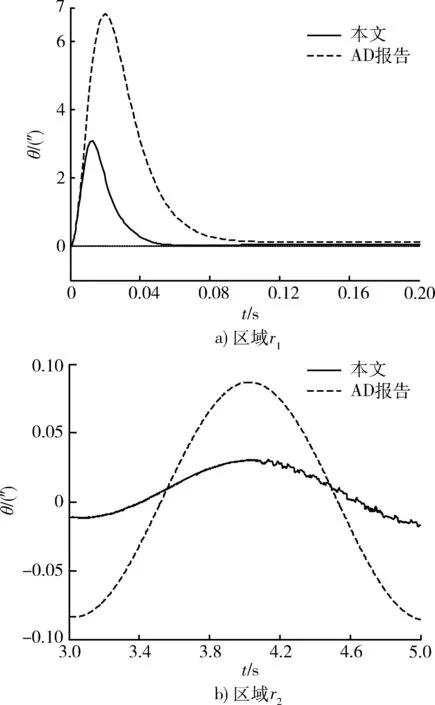
图5　内球转动角度局部放大对比图Fig.5　Zoom in contrast figure of the rotation Angle

图5中的实线和虚线分别是本文和AD报告的仿真实验结果，图5a)反映了系统的动态响应情况。虚线的峰值约为6.8″，峰值时间约为0.02 s，调整时间约为0.1 s；实线的峰值约为3.1″，峰值时间约为0.013 s，调整时间约为0.06 s。滑模控制器与LQR控制器的控制效果相比，峰值降低了54.4%，响应速度提高了近一倍。图5b)反映了系统输出的稳态精度。其中，虚线的稳态误差约为0.09″；实线的稳态误差约为0.03″，稳态精度提高了67%。系统动态响应速度和稳定精度较AD报告均有明显提升。

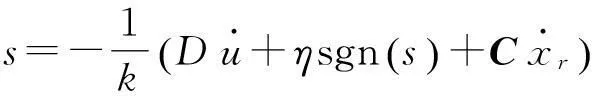
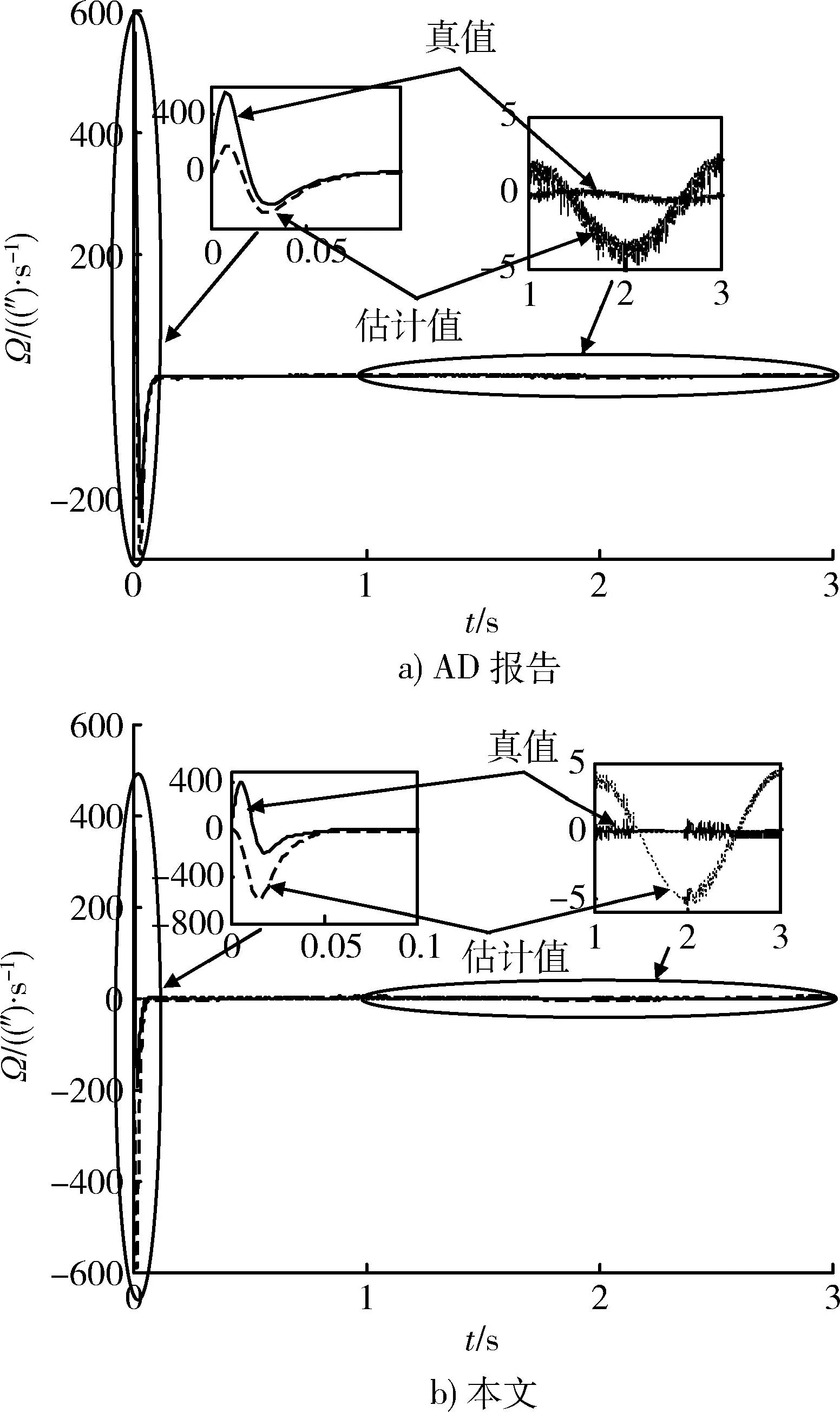
图6　内球转动角速度对比图Fig.6　Rotation angular velocity of the endosphere

图6是内球转动角速度的动态响应曲线，图中还就角速度真值和估计值进行了对比。图6a)中转动角速度真值的峰值约为565(″)∕s，调整时间小于0.1 s，稳态误差约为0.5(″)∕s，角速度估计值的稳态误差约为5(″)∕s。 图6b)中转动角速度真值的峰值约为408(″)∕s，调整时间小于0.05 s，稳态误差约为0.5(″)∕s，角速度估计值的稳态误差约为5(″)∕s。角速度的快速响应体现控制量的及时作用，从图6可以看出，滑模控制方法的角速度快速响应是导致其角度响应加快的原因，响应迅速进一步导致输出峰值较低，系统具有更为优越的动态性能。

4结束语

本文以浮球式惯性稳定平台单轴系统为对象，研究了内球受到外部流场干扰等因素影响时的受力分析，采用滑模控制理论设计了基于比例积分干扰观测器的动态积分滑模控制器，并就其控制性能与AD报告数据进行全面对比和分析。主要结论如下：

(1) 滑模控制具有快速响应的特点，与AD报告相比，角度峰值和响应时间均明显下降，平台的动态性能得到了显著改善；

(2) 采用动态积分滑模控制器后，系统稳态精度较AD报告实验结果得到明显提升，这表明将角度积分项纳入切换面的动态积分滑模控制器可有效提高控制系统稳态精度。

综上所述，本文提出的动态积分滑模控制器可满足动态响应和稳态精度的双重要求，有效实现惯性平台的高精度控制，具有一定的工程应用前景。

参考文献：

[1]FRSTER E R O. Digital IMUE study[R]. CSDLR-841,1974.

[2]张宗美. 浮球平台[J]. 国外导弹与航天运载器,1991(4-5): 1-22.

ZHANG Zong-mei. Floated Inertial Platform [J]. Missiles and Space Vehicles,1991(4-5): 1-22.

[3]李安梁, 蔡洪, 白锡斌. 浮球式惯导平台的自适应模糊滑模稳定控制[J]. 国防科技大学学报, 2013,35(6): 41-43.

LI An-liang, CAI Hong, BAI Xi-bin. Adaptive Fuzzy Sliding Mode Stabilization Control for Floated Inertial Platform[J]. Journal of National University of Defense Technology, 2013,35(6): 41-43.

[4]李安梁,蔡洪,张士峰,等.浮球式惯导平台悬浮稳定问题的动力学建模与控制[J].物理学报,2013,62(15):150203.

LI An-liang, CAI Hong, ZHANG Shi-feng, et al. Control and Modeling of Suspending Stabilization Problom for Floated Inertial Platform [J]. Acta Phys. Sin, 2013,62(15): 150203.

[5]ITKIS U. Control Systems of Variable Structure [M]. New York: Wiley, 1976.

[6]李鹏. 传统和高阶滑模控制研究及其应用[D]. 长沙: 国防科技大学, 2011.

LI Peng. Research and Application of Traditional and Higher-Order Sliding Mode Control[D]. Changsha: National University of Defence Technology,2011.

[7]Yuri B Shtessel. Sliding Mode Stabilization of Three Axis Inertial Platform[C]∥Proceedings of the 26th Southeastern Symposium,1994: 54-58.

[8]Yuri B Shtessel. Decentralized Sliding Mode Control in Inertial Navigation Systems[C]∥Proceedings of the American Control Conference. Washington,1995, 5:3541-3545.

[9]GULLY S W. AIRS Disturbance Characterization Through Single Axis Subsystem Development Tests [R]. AD/ A 013 916,1976.

[10]HILKERT J M. Inertially Stabilized Platform Technology Concept and Principles [J]. IEEE Control Systems Magazine, 2008, 28(1): 26-46.

[11]丁衡高. 惯性技术文集 [M]. 北京: 国防工业出版社, 1994:124.

DING Heng-gao. Inertial Technology Anthology [M]. Beijing: National Defence Industry Press,1994:124.

[12]ALEXANDER N C, STARK H, THORNTON R C.[P] U.S. Patent 3670585,1972.

[13]刘金琨. 滑模变结构控制MATLAB仿真[M]. 北京: 清华大学出版社, 2005:279.

LIU Jin-kun. MATLAB Simulation for Sliding Mode Control[M]. Beijing: Tsinghua University Press,2005:279.

[14]WANG G S, LIANG B, DUAN G R. Parameterization of High Order PI Observers for Second-Order Linear Systems[C]∥ Proceedings of the 25th Chinese Control Conference, Harbin, August 7-11,2006:229.

[15]高为炳. 变结构控制的理论及设计方法[M]. 北京: 科学出版社, 1996:121.

GAO Wei-bing. The Theory and Design Method of Variable Structure Control [M]. Beijing: Science Press,1996:121.

Dynamic Integral Sliding Mode Control Algorithm of Floated Inertial Platform

HU Yue

(PLA，No.92941 Troop,Liaoning Huludao 125000, China)

Abstract:The endosphere of floated inertial platform is the inertial stabilized device. The control precision and fast response of the endosphere restrict each other. The method of how to coordinate the stability and fast response is studied and a dynamic integral sliding mode control algorithm with a proportional integral disturbance observer is presented. The results of the simulation are compared with the LQR control algorithm proposed in the American scientific and technical report. The simulation results show that the control method can improve the control precision of the servo loop of the platform and the performance of the stabilized system.

Key words:floated inertial platform; quick response; integral sliding mode; dynamic sliding mode; disturbance observer; feed forward compensation

*收稿日期：2015-02-16；修回日期：2015-07-15

作者简介：胡悦(1990-)女，江西南昌人。助工，硕士，研究方向为制导、导航与控制。

通信地址：125000辽宁省葫芦岛市92941部队92分队E-mail：hyxslw@163.com

doi:10.3969/j.issn.1009-086x.2016.02.013

中图分类号：V249

文献标志码：A

文章编号：1009-086X(2016)-02-0080-06

导航、制导与控制