基于GPS简易制导火箭弹控制系统设计研究*

杨泗智，王全忠，尹刚，张博浪

(1. 西北工业大学 航天学院，陕西 西安　710072 ；2. 西北工业集团有限公司，陕西 西安　710043)



导弹技术

基于GPS简易制导火箭弹控制系统设计研究*

杨泗智1,2，王全忠2，尹刚2，张博浪2

(1. 西北工业大学 航天学院，陕西 西安710072 ；2. 西北工业集团有限公司，陕西 西安710043)

摘要：提出了一种基于GPS简易制导火箭弹的比例导引加重力补偿的控制方法。制导火箭弹利用GPS的实时测量的飞行状态参数，并与目标的运动状态参数进行对比，生成弹目视线角(line-of-sight,LOS)的变化率，随后按照比例导引律进行制导控制。并利用简易惯导系统进行重力补偿，可以实现纯比例导引律的功能，同时可有效增大末端落角，提高作战毁伤效能，具有一定的工程实际意义。

关键词：全球定位系统；制导火箭弹；比例导引律；重力补偿；惯导；末端落角

0引言

火箭弹能在短时间内将大量弹药投放到敌方阵地，火力猛、威力大，是各国争相发展的炮兵武器[1]。但是由于传统无控火箭弹散布大、精度差，无法满足现代战争对精确打击的要求[2]，为了满足远程精确打击的能力，制导火箭弹的发展适应了现代战争的作战需求，这也促进了炮兵制导火箭弹的出现。本文以某型简易制导火箭弹为背景，研究低成本、高效费比的远程制导火箭弹[3]，为制导火箭弹系统的工程化研制提供理论基础。

1制导火箭系统设计原理

1.1飞行特性分析

制导火箭弹采用弹箭组合的设计模式，在发射前将目标信息及射击诸元装定完毕后，利用火箭动力进行发射，GPS接收机开始实时测量火箭弹的飞行状态参数，待火箭弹飞行到预定速度时实施弹箭分离，将火箭发动机抛掉，火箭弹进入自由飞行状态，这样有利于减小火箭弹气动阻力和提高火箭弹的控制能力。当火箭弹无控飞行至弹道顶点附近时，由预先装定的启控时间感应装置使空间定向陀螺转子解锁，陀螺转子开始高速旋转以保持此时的陀螺惯性轴指向基本不变，随着火箭弹飞行过程中弹体的不断低头，当弹体与陀螺轴夹角达到预定角度时，舵机张开惯导系统开始对火箭弹的飞行进行重力补偿控制，火箭弹在重力补偿条件下按照比例导引律飞向目标[4-5]。

1.2控制系统设计

制导火箭弹的重力补偿控制系统是通过在空间定向陀螺外环轴上安装的接触式传感器确定弹体上的重力方向。通过陀螺外框架上的滑片来敏感弹体纵轴与陀螺惯性轴之间夹角的变化，当弹体姿态角与空间定向陀螺夹角大于设计平衡点时(弹道过于下倾)，升力将增加使弹道上抬；当弹体姿态角与陀螺夹角小于设计平衡点时(弹道过于上抬)，升力将减小使弹道下倾，以闭环方式维持弹丸基本沿直线弹道飞行，实现弹道重力补偿，达到滑翔增程的作用[6]。其控制原理如图1所示。

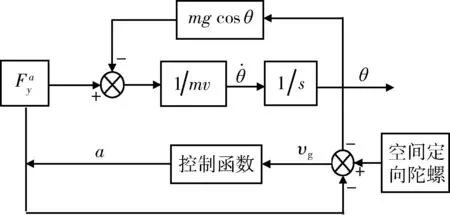
图1　重力补偿控制系统控制原理Fig.1　Control principle of the gravity compensation for control system

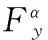
2制导控制系统建模

火箭弹的运动是由弹丸质心运动的动力学方程、弹丸绕质心运动的动力学方程、弹丸质心运动的运动学方程、弹丸绕质心运动的运动学方程以及弹丸相对攻角和相对侧滑角的几何关系方程描述的，按照文献[8-10]建立制导火箭弹的动力学模型。

2.1简易惯导控制系统

制导火箭弹为低速滚转弹，采用鸭舵控制，为了减小体积、和降低成本，采用单通道的控制方式。通过在空间定向陀螺外环轴上安装的接触式传感器可以确定弹体上的重力方向，当弹体处于重力上方区时，控制系统控制舵机打正舵，当弹体处于重力反向区时，控制系统控制舵机打反舵。利用舵机控制补偿重力的法向分量，舵机的控制模型为[11]

(1)

式中：δ为导弹的舵偏角；θg为弹轴与陀螺轴之间的夹角。

由式(1)可以看出：弹体滚转一周，舵机工作两次，产生的空气动力对重力法向分量进行补偿。假设弹体不滚转时，可将弹体滚转一周舵机工作两次的作用效果通过对δ积分等效为舵机的有效舵偏角δyx，其表达式为弹体纵轴与陀螺轴夹角θg的函数。

δyx=Fyδ(θg).

(2)

在不考虑弹体动态特性变化的影响时，攻角与有效舵偏角的关系为(鸭舵控制)

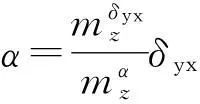
(3)

(4)

2.2比例导引控制

按照比例导引律的定义，需要研究制导火箭弹运动的视线角。为了直观起见，在地面坐标系下火箭弹与目标的相对几何关系如图2所示。

由图2可知，按照制导火箭弹与目标的相对几何关系可以确定，在弹道的纵向和横向平面内的视线角分别为

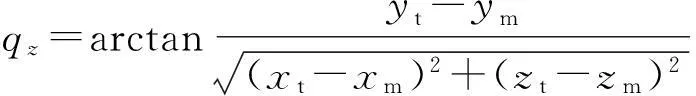
(5)

(6)

图2　制导火箭弹与目标的相对几何关系Fig.2　Relative geometric relations between guided rocket and target

式中：qz，qy为制导火箭弹的纵向和横向的视线角；(xt，yt，zt)为目标在地面坐标系下的坐标值，由火箭弹发射前装定到弹上计算机；xm，ym，zm为火箭弹在地面坐标系下的坐标值，由GPS实时测量信号给出[12-14]，其坐标之间的转换关系详见文献[12]。

对纵向和横向平面内的视线角进行求导，可以得到视线角的变化率为

(7)

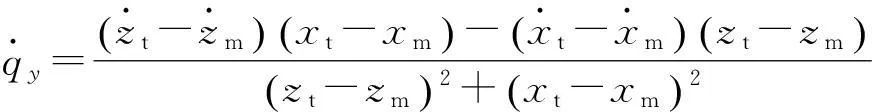
(8)

2.3控制特性分析

按照理想条件下的比例导引律可以知道，导弹速度方向的变化率只与视线角的变化率成正比，而实际中由于重力的存在，对制导律产生一定的影响，因此需要对重力的法向分量进行补偿控制，这里采用末制导炮弹的惯导滑翔控制系统进行设计

按照纯比例导引率设计：弹道倾角的变化率为

(9)

弹道偏角的变化率为

(10)

式中：θ和ψv分别为弹道倾角和偏角；k为比例导引系数；cosθ为坐标转换时俯仰角对偏航速度矢量的耦合影响。

在不考虑重力影响的情况下导弹动力学模型为

(11)

(12)

式中：Fy，Fz分别为由比例导引控制引起的纵向和横向的控制力，由导弹按照比例导引信号控制执行机构产生。

导弹在飞行过程中在纵向弹道面内不可避免地要受到重力的影响，不能够满足理想比例导引控制，在重力法向分量的影响下其弹道倾角变化率为

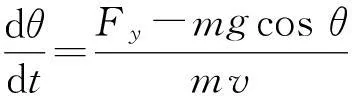
(13)

增加重力补偿时，弹道倾角变化率为

(14)

当Ybc=mgcosθ时，为重力补偿系统；当Ybc>mgcosθ时，为过重力补偿系统；当Ybc

由于重力补偿系统采用了惯导陀螺闭环控制，控制输入为陀螺轴与弹轴之间夹角，一般为重力补偿[15]，但是可以按照实际需要对陀螺与弹轴间夹角ϑg进行重新设置，也可通过调整装定参数(陀螺启控时间)来改变控制角度。

3仿真分析

这里以某制导火箭弹的设计参数为例进行仿真分析。首先定义地面坐标系Oxyz，坐标原点O选择在火箭弹发射点，Ox轴为弹道面与水平面的交线指向目标为正，Oy轴沿垂线向上，Oz轴与其他2轴垂直并构成右手坐标系。仿真的初始条件如下：目标点在地面坐标系下的坐标值为x=50 km，y=0 m，z=5 km，火箭弹的物理量参数和气动参数采用实测和吹风试验值，发动机推力采用点火试验数据，当火箭弹飞行速度达到1 050 m/s时，发动机工作结束，弹箭分离，火箭弹进入被动飞行段，当制导火箭弹飞行时间达到50 s时，比例导引控制系统开始工作，设定比例导引系数k=4，分3种情况进行仿真分析，即：不考虑重力的影响时的纯比例导引控制，考虑重力影响时的比例导引控制和考虑重力影响但增加重力补偿控制的比例导引控制。

仿真分析结果如下：

(1) 不考虑重力的影响时，按照纯比例导引律控制，仿真结果如图3～6所示。

图3　纯比例导引条件下的射程Fig.3　Range under pure proportional navigation

图4　纯比例导引条件下的侧向修正Fig.4　Lateral correction under pure proportional navigation

图5　纯比例导引速度变化曲线Fig.5　Curve of velocity changing under pure proportional navigation

图6　纯比例导引弹道倾角变化曲线Fig.6　Curve of trajectory angle changing under pure proportional navigation

通过图3～6可以看出在纯比例导引控制条件下，制导火箭弹在能够有效的时间内准确到达目标点位置，弹道倾角处于一直往上抬的趋势，导弹的落角为-11.2°。

(2) 考虑重力的影响时，采用比例导引控制，仿真结果如图7～10所示。

图7　在重力影响下比例导引射程Fig.7　Range of proportional navigation under the influence of gravity

图8　重力影响下比例导引侧向修正Fig.8　Lateral correction of proportional navigation under the influence of gravity

图9　重力影响下比例导引速度变化曲线Fig.9　Curve of velocity changing of the proportional under the influence of gravity

图10　重力影响下比例导引弹道倾角变化曲线Fig.10　Curve of trajectory angle changing of the proportional under the influence of gravity

通过图7～10可以看出，在考虑重力影响时，与无控弹道对比制导火箭弹按照比例导引律进行了修正控制，但在修正过程中由于受到重力法向分量的影响导致火箭弹而提前落地，射程方向飞了42 312 m，侧偏方向1 058 m，没有到达预定的目标点。因此，为了导弹能够顺利到达目标点位置需要进行重力补偿控制。

(3) 在考虑重力影响和进行重力补偿控制的条件下采用比例导引控制，结果如图11～14所示。

图11　在重力补偿条件下比例导引射程Fig.11　Range of proportional navigation >under the gravity compensation

图12　在重力补偿条件下比例导引侧向修正Fig.12　Lateral correction of proportional navigation under the gravity compensation

图13　在重力补偿条件下比例导引速度随变化曲线Fig.13　Curve of velocity changing of the proportional under the gravity compensation

图14　在重力补偿条件下比例导引弹道倾角变化曲线Fig.14　Curve of trajectory angle changing of the proportional under the gravity compensation

通过图11～14可以看出，制导火箭弹在有重力补偿的条件下可以有效地进行制导控制，能够准确到达目标点位置，并且落角接近-30°，相对于纯比例导引律对装甲目标的毁伤效能方面有较大提高。

通过上述仿真可以看出：对于GPS制导火箭弹采用比例导引律进行控制，当不考虑重力影响的时候，火箭弹可以准确到达目标位置。当考虑重力影响时，火箭弹由于受到重力法向分量的影响而提前落地，而达不到预定的射程和修偏。为了消除重力的影响，这里采用了重力补偿控制，在比例导引回路中加入过重力补偿信号，就会使弹道在比例导引初始阶段向上抬起，同时又由于闭环比例导引律的作用使弹道向回拉，这样弹道末段倾角就会增大，从而增大导弹的落角，提高对目标的毁伤效能。

4结束语

本文通过对GPS制导火箭弹的飞行特性分析，建立了制导控制系统的数学模型，研究了重力的法向分量对制导火箭弹在比例导引控制的影响，提出了重力补偿控制方案，并通过数学仿真分析证明了重力补偿方案的可行性，通过仿真分析认为在有重力补偿的条件下，导弹不仅可以有效命中目标，并且可以提高导弹落角，达到提高作战效能的目的，具有一定的工程实际意义。当然在制导律研究中主要是以理论化研究为主，没有考虑工程实际如制导控制系统的控制能力饱和、GPS误差影响以及惯导陀螺漂移等因素的影响，后续研究中再进一步完善。

参考文献：

[1]张成. 大机动制导火箭弹控制方法研究[J].北京理工大学学报，2010, 30(12)：1432-1435.

ZHANG Cheng. Research on Guided-Rockets of Maneuvering Control System Design Transactions[J] .Beijing Institute of Technology，2010,30(12):1432-1435.

[2]佘浩平，杨树兴. 基于GPS/INS的制导型火箭弹系统概念设计[J].弹箭与制导学报，2003，23(4)：173-175.

SHE Hao-ping, YANG Shu-xing. System Concept Design of the Guided Artillery Rocket Based on GPS/INS[J]. Journal of Projectiles, Rockets, Missiles and Guidance， 2003，23(4)：173-175.

[3]杨泗智,胡宽荣.远程火箭弹滑翔增程技术研究[J].现代防御技术，2011，39(4)：15-18.

YANG Si-zhi,HU Kuan-rong. Research on Gliding Extended Range in Long Rang Rocket Missile[J]. Modern Defence Technology,2011,39(4):15-18.

[4]杨洋.GPS/INS深组合导航中的关键技术研究[D].南京：南京理工大学,2013:4-11.

YANG yang.Research on the Key Technologies of SINS/GPS Deeply Coupled Navigation System[D]. Nanjing:Nanjing University of Science & Technology,2013:4-11.

[5]丁传炳,王良明,郑翠翠.过重力补偿GPS/INS末制导炮弹弹道仿真研究[J].飞行力学,2010,28(5):47-50.

DING Chuan-bing, WANG Liang-ming, ZHENG Cui-cui. The Research of Trajectory Simulation of Gravity Compensation GPS/INS Terminal Guided Projectile[J]. Flight Dynamics,2010,28(5):47-50.

[6]牟宇,祁载康,林德福.末制导炮弹惯性制导仿真及横向散布研究[J].系统仿真学报,2009 ,21(20):6560-6563.

MOU Yu, QI Zai-kang, LIN De-fu. Terminal Guided Projectile Inertial Navigation Simulation and Lateral Distribution Study[J]. Journal of System Simulation, 2009, 21(20):6560-6563.

[7]张建伟,黄树彩,韩朝超. 基于Matlab的比例导引弹道仿真分析[J].战术导弹技术,2009,1(3):60-64.

ZHANG Jian-wei, HUANG Shu-cai, HAN Chao-chao. Analysis of Trajectory Simulation of Proportional Guidance Based on Matlab[J].Tactical Missile Technology,2009,1(3):60-64.

[8]钱杏芳, 林瑞雄, 赵亚男.导弹飞行力学[M].北京:北京理工大学出版社,2000：42-48.

QIAN Xing-fang,LIN Rui-Xiong, ZHAO Ya-nan. Missile Flight Mechanics [M]. Beijing: Beijing Institute of Technology Press，2000：42-48.

[9]张有济.战术导弹飞行力学设计(上)[M].北京:宇航出版,1998：90-121.

ZHANG You-ji. Flight Mechanics Design of Tactical Missile(UP) [M].Beijing: Aerospace Publishing, 1998:90-121.

[10]丁传炳.制导弹箭弹道测量及弹道重构技术研究[D]. 南京：南京理工大学, 2011：11-22.

DING Chuan-bing. Investigation on Ballistic Measurement and Teehnology of Trajectory Reconstruction for Guided Projectile[D]. Nanjing:Nanjing University of Science &Technology,2011：11-22.

[11]唐成荣,宋卫东,许芹祖,等. 某型激光末制导炮弹六自由度弹道仿真[J].科学技术与工程,2010, 26(10):6453-6456.

TANG Cheng-rong, SONG Wei-dong, XU Qin-zu. A Type of Laser Terminal Guided Projectile Six Degree of Freedom Trajectory Simulation[J]. Science Technology and Engineering, 2010, 26(10):6453-6456.

[12]宋伟锋，杨泗智，王全忠,等. GPS 在制导火箭弹中应用研究[J]. 沈阳理工大学学报，2013,32(5):59-63.

SONG Wei-feng，YANG Si-zhi，WANG Quan-zhong.et al. Coordinate Transformation Analysis of GPS Applied in Guidance Rocket Missile[J]. Journal of Shenyang Ligong University, 2013,32(5):59-63.

[13]CHWA D Y, CHOI J Y, ANAVATTI S G. Observer Based Adaptive Guidance Law Considering Target Uncertainties and Control Loop Dynamics[J]. IEEE Transactions on Control Systems Technology, 2006,14(1): 112-117.

[14]李辉,王子滨. 国外GPS/INS复合制导技术的发展[J].现代防御技术,2004,32(2):50-59.

LI Hui ,WANG Zi-bin. Development of GPS/INS Composite Guidance Technique Abroad[J]. Modern Defence Technology，2004,32(2)：50-59.

[15]林德福,祁载康,夏群力.带过重力补偿的比例导引制导律参数设计与辨识[J].系统仿真学报, 2006,18(10):2753-2755.

LIN De-fu，QI Zai-kang，XIA Qun-li. Design and Identification on Parameters of Proportional Navigation Guidance Law with Gravity Over Compensation[J]. Journal of System Simulation,2006,18(10):2753-2755.

Control System Design of Simple Guided Rocket Based on GPS

YANG Si-zhi1，2，WANG Quan-zhong2,YIN Gang2,ZHANG Bo-lang2

(1.Northwestern Polytechnical University, School of Astronautics，Shanxi Xi’an 710072，China；2.Northwest Industry Company LTD, Shaanxi Xi’an 710043，China)

Abstract:A design principle of the proportional navigation and the gravity compensation for the guided rocket has been proposed. The guided rocket makes use of real time flight information measured by GPS, and is compared with the motion state information of the target, which generates the rate of the line of sight (LOS). According to the proportional guidance law for guidance and control, a simple inertial navigation system for gravity compensation is used, which can realize the function of the pure proportional guidance law, and at the same time can enlarge the terminal angle, and effectively improve the combat damage effectiveness. The principle has some actual engineering significance.

Key words:globle position system(GPS)；guided rocket;proportional guidance law;gravity compensation;inertial navigation;terminal angle

*收稿日期：2015-06-03；修回日期：2015-07-07

作者简介：杨泗智(1981-)，男，江苏赣榆人。高工，博士生，主要研究方向为导弹总体设计。

通信地址：710043陕西省西安市幸福南路1号设计一所E-mail：yangsizhi00124@163.com

doi:10.3969/j.issn.1009-086x.2016.02.009

中图分类号：TJ765.2

文献标志码：A

文章编号：1009-086X(2016)-02-0055-06