“回归思维”在高中物理中的应用

梁隆畔

摘 要：针对农村中学学生基础差，对一些物理基本概念掌握不透彻的情况，笔者进行思维的救助，从根本上要求学生弄懂相关概念，便于在分析题的时候能快速回归到概念或模型，迅速得出解题思路，而不会在读题与审题边缘徘徊，影响解题效率。

關键词：回归思维；模型；学习方法

同学们，你还在为学习方法的选择不当而困扰吗？还在为你在学习上付出的与收获的不成正比而埋怨吗？如果有，不妨挤点时间来相互探讨一下学习的方法。

学习本无定法，但有一定规律的准则，在我们每个学科的学习中，不难发现，知识都是由简单到复杂，层层推进，而在逐渐深入学习的过程中，前面的知识无时无刻都贯穿其中，这就是我们知识呈现的一定规律，由简到繁，最后体现基础知识的综合运用。

掌握了基础知识以及它们的一般规律，我们还得加以熟练地运用。谈到知识的运用，这就是我们的问题了，在我们大多学生中，上课都能听懂老师的讲解，但要自己亲自去解决实际问题，则是丈二的和尚（摸不着头脑）。

我们在处理问题时，一般会出现混轮、定势和模糊效应，也就是当花很多时间把题做出来时，自己心中并没有多大把握是正确的，这样“运用”知识会有怎样的效果呢？当然没有多大的效果。

运用知识的前提是熟练掌握知识，在掌握的基础上就得辅以适当的方法。方法有千百种，该选哪一种才适合自己呢？针对知识呈现的相关规律，我们就其回归思维方法与大家分享一下。

所谓回归，就是把问题回归到每个相联系的基本知识，他们是基本概念或基本公式，而不是单纯的停留在问题这个层面上去思考。

例如，在判断物体是否运动时，只要把机械运动的定义（一物体相对另一物体位置的变化）搬出来，结果显然就出来了，而不管问题的情景怎么设置都逃不了基本的定义。再如，在理解物体运动的加速度时，回归到加速度的比值定义（速度随时间的变化量），意思就是只要速度随时间在变化（包括速度的方向），物体就具有加速度，而它的物理意义是“单位时间里速度的改变量”，同时再顺便掌握加速度的方向与速度变化的方向始终一致，从这两方面去掌握加速度的本质，在应用中就游刃有余。这些就是回归思维，而我们在实际应用时还会碰到很多类似的问题，遇到时用它来处理相关题型是很快捷方便的。

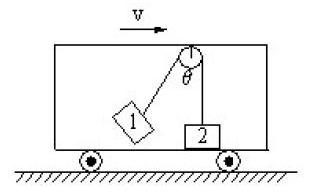
错误的受力分析：一些学生在分析物体2受力时，由于它具有向右的加速度，会在水平方向上画出一个水平向右的力叫驱动力，摩擦力水平向左，说是这两个力的合力水平向右，提供物体2的加速度，这位同学在受力分析时，思维混乱，没有回归到产生力的本质上来，想当然的多画出一些力来，导致分析错误，出现这种思维混乱不清，是基础知识掌握不牢的表现。而正确的受力分析应该是：

物体1：竖直方向所受的重力和沿轻绳斜向上绳子的弹力（拉力），这两个力的合力水平向右，提供物体1水平向右的加速度，结合三角形定则，得出 ，绳子的拉力为 。

物体2：竖直向下的重力，竖直向上的支持力和绳子的拉力， 平衡式为；水平方向受水平向右的静摩擦力，由水平方向牛顿第二定律得：，由于物体1和物体2加速度相同，所以。

正确答案：BD

反思：本题考查的知识点有：牛顿第二定律的应用、由运动状态判断静摩擦力产生的方向以及大小计算和受力分析图在实际问题中的正确画法，属于连接体模型，偏简单，应要求学生熟练掌握此类题型的分析思路。

在物理计算题这一块，一般是考查知识的综合运用能力，归根结底也是基础知识掌握是否牢固的宏观体现。在处理这类问题时，可以把每个大问题进行小知识的关联回归，再用相对应的关系串成一条线，最后直指向问题本身。如在牛顿运动定律、运动学和动力学的综合运用中，有两种体现规律的模式，即通过运动学物理量求力学物理量和通过力学量求运动量，这两类问题都是借助牛顿第二定律这个动力学公式把运动学和动力学很好的联系起来，每遇到此类问题时，只要我们进行这种具有规律性模式的回归，相信在解决问题的路上会有很多惊喜。

学习本无定法，但有些规律性的东西值得我们去思考和总结，不仅物理，我们学习的每一个科目，在理解掌握相关知识时进行基本概念和规律的回归是很有必要的，这种回归被使用巧妙时，它不仅是一种思维方法，更是一种解题的妙招！