波浪对隔水管-导管系统横向动态性能影响分析
2016-07-20樊洪海沈维格田得强刘玉含文子祥
邓 嵩,樊洪海,沈维格,田得强,刘玉含,文子祥
(1.中国石油大学(北京) 油气资源与探测国家重点实验室,北京 102249;2.中国石油 长城钻探工程有限公司,辽宁 盘锦 124010)①
波浪对隔水管-导管系统横向动态性能影响分析
邓嵩1,樊洪海1,沈维格2,田得强1,刘玉含1,文子祥1
(1.中国石油大学(北京) 油气资源与探测国家重点实验室,北京 102249;2.中国石油 长城钻探工程有限公司,辽宁 盘锦 124010)①
摘要:基于哈密顿原理建立了多因素的深水钻井隔水管-导管系统横向振动方程,在求取系统动能时,综合考虑管内流体流速、管外附属管线和附连水质量的影响;在求取势能时考虑了隔水管-导管弯曲伸长产生的附加拉力;在求取外力虚功时考虑了浅层土的横向载荷作用。选取了一口深水典型井进行实例分析,建立土-弹簧模型求取浅层土横向载荷,运用Block Lanczos法提取隔水管-导管系统的固有频率,并分析了不同条件对固有频率的影响。根据波浪的特性,利用Abaqus软件编制程序得出了时域上波浪高度和波浪周期对隔水管-导管系统的横向动态力学性能影响。
关键词:波浪;隔水管;导管;管土;时域
超深水环境下,深水钻井隔水管与海水直接接触,随着水深的增加海洋环境愈发复杂多变,海洋载荷对深水钻井管柱稳定性的影响也越来越大[1-2],同时深水导管下入在浅层胶结强度很弱的浅层土中,也减弱了深水钻井管柱的稳定性。国内外研究学者近年来对深水钻井隔水管、导管做了一些研究,Ljustina[3]等人用非线性数学模型完成隔水管系统的静态力学分析,得到隔水管横向位移、转角、轴向力、弯矩、剪力、自振频率;Chen Yanfei等人[4]采用微分变换法求解了海洋立管的自然频率和模态振型,并基于不同的边界条件进行了分析和求解;王海峡等[5-6]建立了充液隔水管的非线性振动模型,计算了张力比、管长、浮力块等对隔水管固有频率的影响;王宴滨等[7]研制了关于深水钻采管柱力学行为的试验装置,以便研究其动态性能;A.Moghiseh等人[8]建立了二维平面内受平台运动、波浪力和海流力作用的隔水管振动问题。以上学者对于隔水管以及导管稳定性问题都进行了详尽的研究,但是没有把隔水管-导管作为一个整体系统研究,他们通常将隔水管的底端采用固定球铰模拟。但实际作业中,海底浅层土的强度很低,水下井口与导管在海底泥线或以下容易发生沉降、弯曲倾斜和侧向变形,这些因素导致以固定球铰为下边界条件的计算结果不准确。孙友义[9]在2009年分析了隔水管-导管系统的静态性能和模态性能,对整体分析和解耦分析的结果进行对比,但是并没有具体展示系统的动态性能计算方法以及模拟结果。本文在前人研究的基础上,基于哈密顿原理建立隔水管-导管整体的动态微分方程,考虑多种工程因素的影响,并通过Abaqus软件编制程序计算得出波浪对隔水管-导管在时域上的影响,为深水钻井提供参考。
1系统横向动态微分方程
深水钻井隔水管-导管系统受力如图1所示。
基于哈密顿原理建立的隔水管-导管系统的微分方程为
(1)
式中:t1,t2为系统振动的任意时刻,s;K为动能,J;U为势能,J;δW为虚功,J。
式(1)表示为:时间变化引起的动能和势能的变化及由外部载荷所做的虚功之和为零。
1.1系统动能及变分
隔水管-导管系统在波浪交变载荷、海流、海底浅层土等作用下发生振动和偏移,并使隔水管-导管管体产生动能。设单位长度dz的隔水管-导管单元的动能dKr为:
(2)
式中:mp为单位长度的隔水管-导管的振动质量,kg。
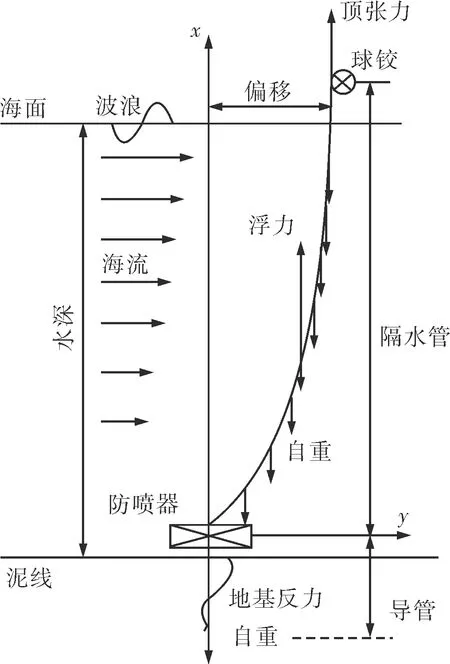
图1 深水钻井隔水管-导管系统
隔水管-导管系统内流体沿管柱流动的同时也会随着隔水管-导管的横向振动而发生牵连运动,流体的横向振动同样会导致管柱系统的横向振动。设管内流体流速为v,假设管柱振动幅度很小,则有dy/dz≤1,可得:
(3)
单位长度隔水管-导管系统内流体的动能dKf为
(4)
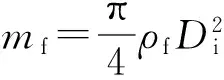
隔水管-导管系统的动能为
(5)
在任意时刻t1到t2,由时间变化引起的动能K的变化为
(6)
由于常数的变分为零,对式(6)根据变分运算法则展开并做分部积分,再根据变分δy在时间边界和位置边界上的值为零,得:
(7)
1.2系统势能及变分
设系统受弯矩M作用,隔水管-导管单元dz的弯曲势能dUM为
(8)
式中:E为隔水管-导管的弹性模量,GPa;I为隔水管-导管的转动惯量,m4。
隔水管-导管管体的轴向力因轴线的弯曲而引起附加力矩,则位置为z处的隔水管-导管单元受到的势能dUT为
(9)
式中:Te为隔水管-导管系统的有效轴向力,kN。
长度为l的隔水管-导管系统总势能为
Te(z,t)(y′)2]dz
(10)
任意时刻t1到t2由时间变化引起的势能变化为
(11)
由于常数的变分为零,对式(11)根据变分运算法则展开并做分部积分,再根据变分dy在时间边界和位置边界上的值为零,得:
(12)
1.3系统外力的虚功及变分
隔水管-导管系统承受的环境载荷主要为随时间变化的横向载荷F(z,t),包括波流载荷、海底浅层土抗力和管柱与内流体的阻尼力等,他们都对隔水管-导管系统做功。
作用于隔水管-导管单元上的横向载荷F(z,t)做的虚功为
δdWF=F(z,t)δydz
(13)
海面至海底泥线,采用修正的Morison方程[10]计算的波流载荷作为横向载荷;海底泥线以下,采用p-y曲线的方法[11]计算管土相互作用载荷。
在任意时刻t1到t2,由时间变化引起的虚功W的变化为
(14)
1.4动态方程
将式(7)、(14)、(16)代入哈密顿方程,整理得:
mfv2y″]δydzdt+
(15)
由于δ的任意性,去掉积分符号,最终得到深水钻井隔水管-导管系统横向振动方程为
(16)
2模拟实例
为了研究隔水管-导管系统的静态力学性能,针对某水深钻井隔水管-导管系统做数值模拟,水深为1 000 m。隔水管-导管系统的配置如表 1所示[12]。
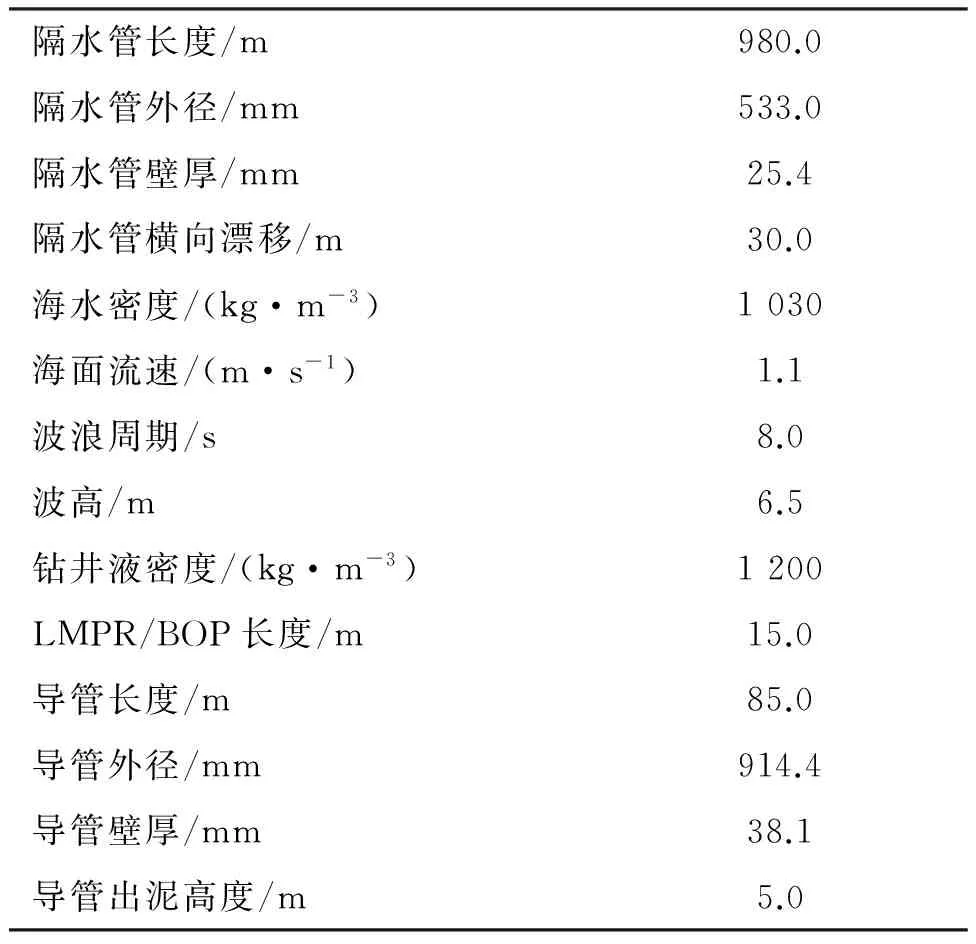
表1 隔水管-导管系统配置
假设隔水管-导管系统为弹性材料,泥线至泥线以下100 m均为黏土层。其材料属性如表2所示。

表2 隔水管-导管材料属性
2.1管土模型模拟
本文采用更符合浅层土实际的土-弹簧模型[13]模拟管土相互作用,泥线以下的导管被转换成插入土壤中的等强度梁。根据表2海底浅层土数据建立模型,如图2所示。
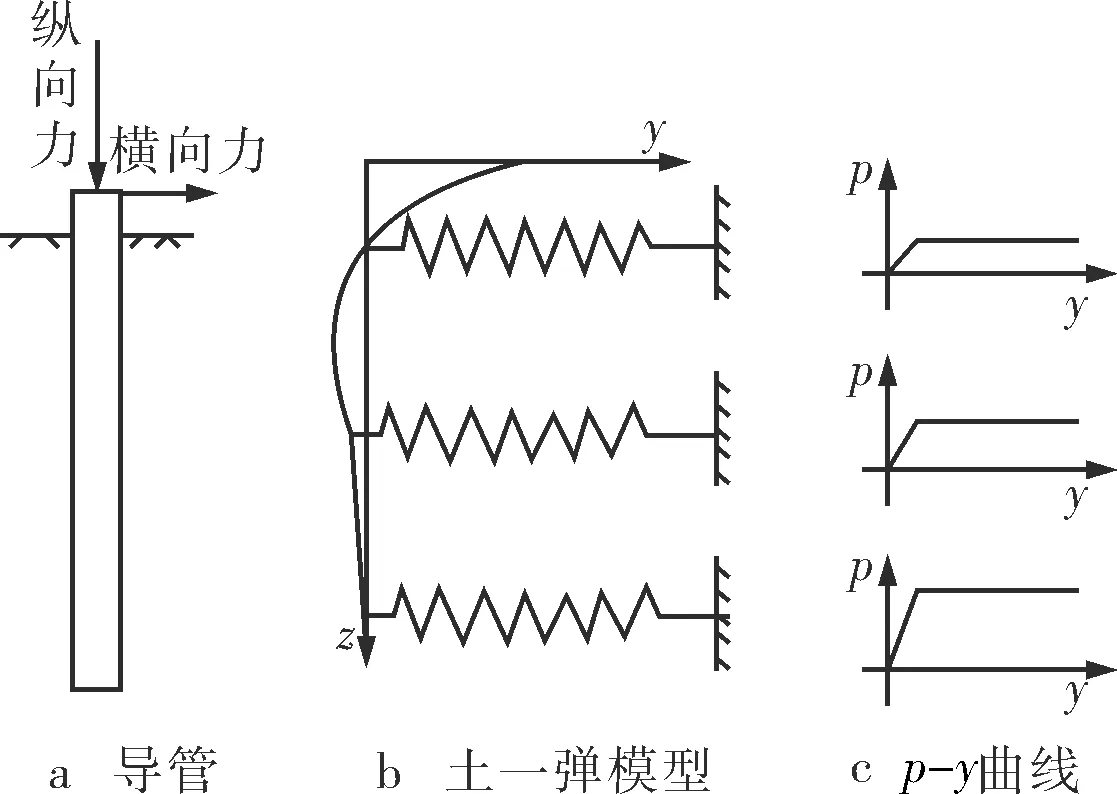
图2 管土相互作用土-弹簧模型
运用Abaqus软件进行编程,可得出浅层土的p-y曲线,如图3所示。

图3 海底不同深度土层的p-y曲线
2.2自由振动分析
对于隔水管-导管系统的自由振动,固有频率与其结构和边界条件有关,而与外部载荷无关。选用Block Lanczos法[14]提取管柱系统的固有频率,如表3所示。

表3 隔水管-导管系统各阶固有频率
隔水管-导管系统的前5阶模态振型如图4所示。导管的挠度很小,说明在管土的作用下,导管出现大幅度横向变形的概率很低。对于隔水管段,1阶模态时,隔水管横向变形的最大部位出现在隔水管中部;2阶模态时,隔水管横向变形的最大部位出现在距海面1/4h和3/4h处;3阶模态时,隔水管横向变形的最大部位出现在距离海面1/6h、1/2h以及5/6h。由此可知,隔水管横向变形的最大部位将随着模态阶数的增加而遍布隔水管各个位置。
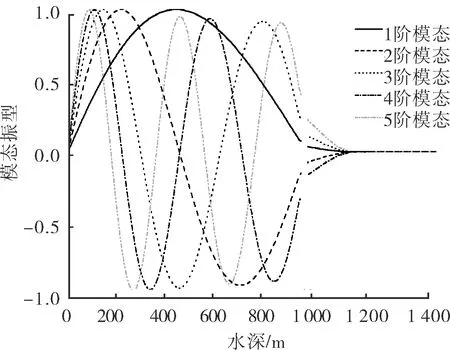
图4 隔水管-导管系统前5阶模态振型
2.3动态性能影响分析
在隔水管-导管系统的动态力学分析中,波浪的动态运动是重要的影响因素。随机的波浪力作用导致隔水管-导管系统的动态力学性能呈现出复杂性和随机性,结合实例中管土作用结果,自由振动分析结果,运用Abaqus软件进行求解计算,最终得到海洋载荷对隔水管-导管系统的动态性能影响结果,如图5~6所示。
图5为波浪高度对隔水管-导管系统横向动态性能影响的计算结果。隔水管底部球铰的转角在20 s后接近稳定横向振动,最大横向变形在10 s后接近稳定横向振动。隔水管底部球铰转角和隔水管-导管系统最大横向变形(水下33 m)随着波浪高度的增加而增大,但幅度不大,转角变化小于0.03°,横向变形变化小于0.04 m。
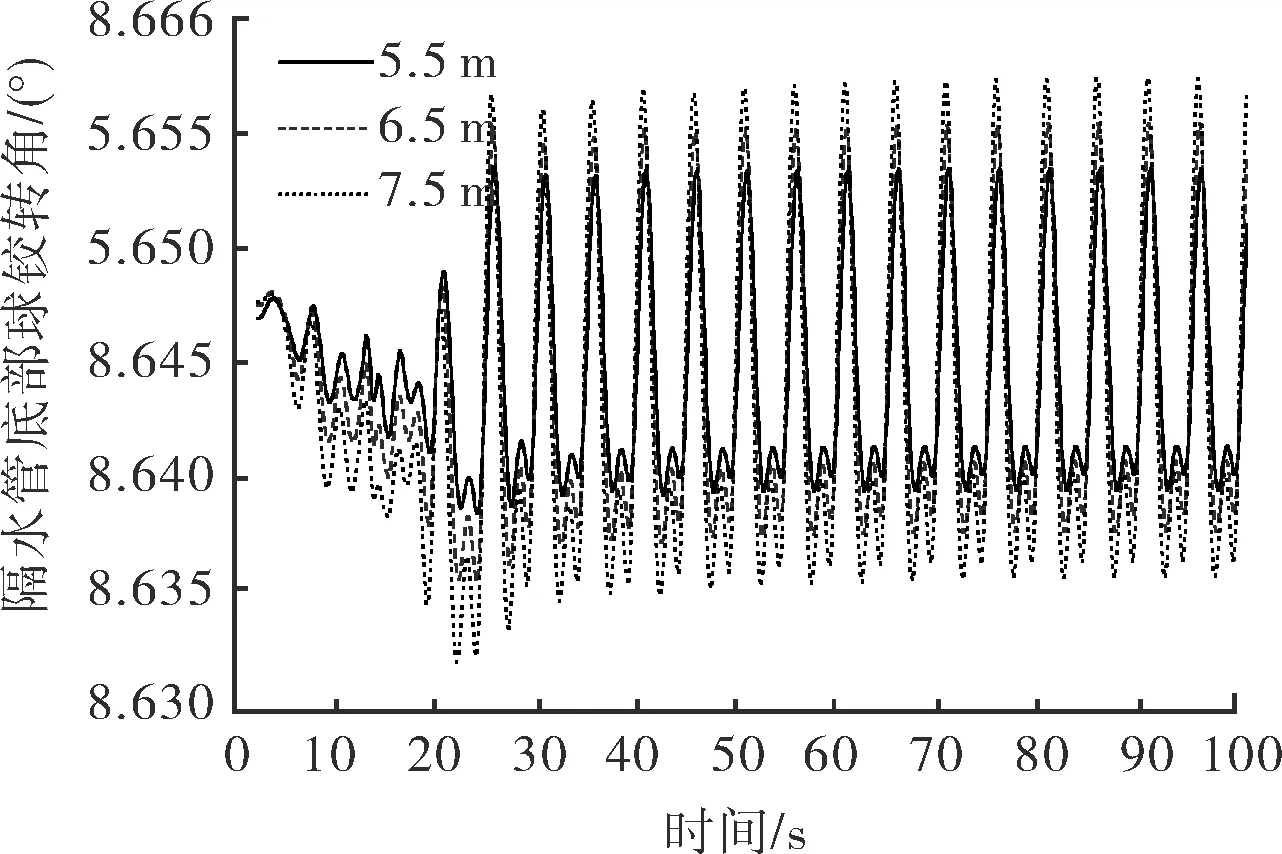
a 隔水管底部球铰转角
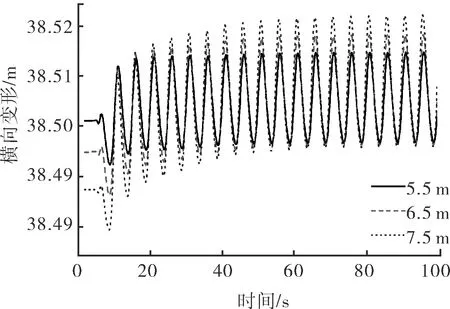
b 横向变形
图6为波浪周期对隔水管-导管系统横向动态性能影响的计算结果。隔水管底部球铰的转角在20 s后接近稳定横向振动,最大横向变形在10 s后接近稳定横向振动。波浪周期的变化对隔水管-导管系统横向动态性能有显著影响。最大的隔水管底部球铰转角变化接近0.1°,最大横向变形的变化约为0.3 m。
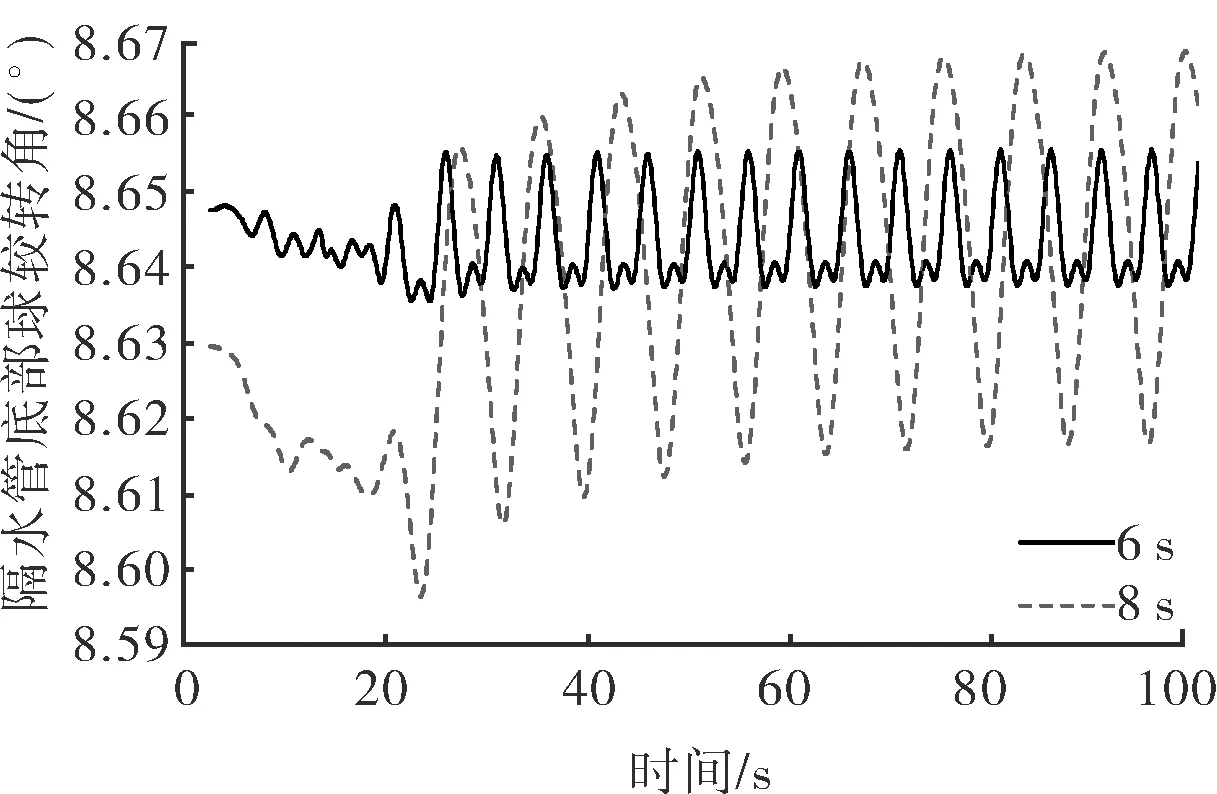
a 隔水管底部球铰转角
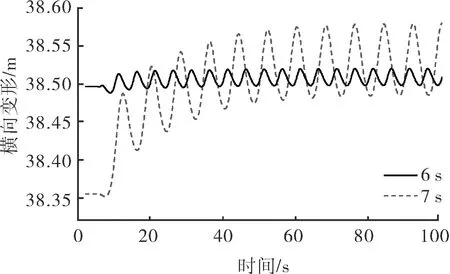
b 横向变形
3结论
运用哈密顿原理推导出深水钻井隔水管-导管系统横向非线性四阶微分方程,基于Abaqus软件,确定隔水管-导管系统的固有频率以及浅层管柱的横向载荷。分析了波浪高度、波浪周期等海洋环境因素对深水钻井隔水管-导管系统的非线性动态性能的影响,得出如下结论:
1)隔水管-导管系统中导管的挠度较小,说明在管土的作用下,导管出现大幅度横向变形的概率较低。
2)从海洋载荷在时域上对系统的影响分析来看,其对深水钻井隔水管-导管系统的横向动态性能影响较大,波浪周期变化对于系统稳定性的影响显著高于波浪高度变化的影响。
3)实例井的隔水管-导管系统的最大横线变形发生在水下33 m处,承受的最大应力在10~30 m。在实际作业中,需要对两处重点监测,防范于未然。
4)本文只计算了波浪对隔水管-导管系统的影响,只是作为动态分析的初步探索,下一步应该讨论多种模型对比,并且考虑更多因素的影响,例如钻井平台升沉运动,海底地震作用等。
参考文献:
[1]兰洪波,张玉霖,菅志军,等.深水钻井隔水管的应用及发展趋势[ J].石油矿场机械,2008,37(3):96-98.
[2]畅元江,陈国明,许亮斌,等.超深水钻井隔水管设计影响因素[J].石油勘探与开发,2009 (4):523-528.
[3]Lju stina A M,Parunov J,Senjnovi I.Static and Dynamic Analysis of Marine Risers[C]//Proceedings of the 16th Symposium of Theory and Practice of Shipbuilding.Zagreb,2004.
[4]Chen Y,Chai Y H,Li X,et al.An extraction of the natural frequencies and mode shapes of marine risers by the method of differential transformation[J].Computers & Structures,2009,87(21):1384-1393.
[5]王海峡,赵广慧.波流极值载荷作用下隔水管的非线性分析[ J].石油矿场机械,2008,37(11):6-10.
[6]王海峡,赵广慧,余长柏,等.充液钻井隔水管的非线性动力特性分析[J].石油矿场机械,2010,39(5):14-16.
[7]王宴滨,高德利,房军.深水钻采管柱力学行为模拟试验系统研制[J].石油矿场机械,2014,43(4):26-29.
[8]Moghiseh A,Chaloshtory H R,Rahi A.Effect of Middle Tension on Dynamic Behavior of Marin Risers[J].Journal of Maritime Research,2014,9(1):63-70.
[9]孙友义.深水钻井隔水管强度评价方法及应用研究[D].东营:中国石油大学,2009.
[10]Han S M,Benaroya H.Non-linear coupled transverse and axial vibration of a compliant structure,part 2:forced vibration[J].Journal of Sound and Vibration,2000,237(5):875-900.
Influence Analysis of Waves Loading on Lateral Dynamic Performance of Riser-conductor System
DENG Song1,FAN Honghai1,SHEN Weige2,TIAN Deqiang1,LIU Yuhan1,WEN Zixiang1
(1.StateKeyLaboratoryofPetroleumResourcesandProspecting,ChinaUniversityofPetroleum,Beijing102249,China;2.GreatWallDrillingCorporation,PetroChina,Panjin124010,China)
Abstract:The lateral vibration equation of a deepwater drilling riser system with multiple factors is established based on the Hamilton principle in this paper.The effects of the flow velocity,the tube flow velocity,the tube and the attached water quality are considered in the kinetic energy of the system.In the calculation of the potential energy,the additional tensile force of the pipe - pipe bending elongation is considered.And the lateral load of shallow soil is considered when calculating the external force.And then a typical wells in deepwater is selected to carry out an example analysis,a soil - spring model is established to get the shallow layer soil lateral load,and the natural frequency of the riser pipe system is extracted by using Block Lanczos method in this paper.The influence of different conditions on the natural frequency is analyzed according to the characteristics of wave by the Abaqus compile the Python language in the time domain in the end.The conclusion shows that the effect of wave height and wave period on the lateral dynamic mechanical properties of the riser duct system.
Keywords:wave;riser;conductor;casing-soil;time domain
文章编号:1001-3482(2016)06-0007-06
收稿日期:2015-12-25
基金项目:国家自然科学基金“深水钻井隔水管-导(套)管力学特性研究与水下井口稳定性分析”(51574261);国家自然科学创新研究群体“复杂油气井钻井与完井基础研究”(51221003)
作者简介:邓嵩(1989-),男,博士研究生,主要从事深水钻完井管柱力学与地层三压力分析研究,E-mail:13699286998@126.com。
中图分类号:TE951
文献标识码:A
doi:10.3969/j.issn.1001-3482.2016.06.002
