四履带张紧器恒张力控制建模与仿真

万箭波，王福山，王海玲，周军峰，李怀亮，王　徽，王东峰

(1.天津市精研工程机械传动有限公司，天津 300409；2.天津工程机械研究院，天津 300409；3.海洋石油工程股份有限公司，天津 300451)



o设计计算o

四履带张紧器恒张力控制建模与仿真

万箭波1，王福山2，王海玲2，周军峰1，李怀亮3，王徽1，王东峰1

(1.天津市精研工程机械传动有限公司，天津 300409；2.天津工程机械研究院，天津 300409；3.海洋石油工程股份有限公司，天津 300451)

摘要：四履带张紧器是深海脐带缆铺设系统中的关键设备，而恒张力控制技术是张紧器的核心技术。通过分析张紧器的恒张力控制系统，提出了四履带张紧器的恒张力控制数学模型。利用AMESim软件搭建四履带张紧器的恒张力控制系统模型，仿真验证了恒张力控制的有效性，研究了张紧器在不同海况下恒张力控制参数的设定规律，为进一步研究PID自适应控制算法提供分析数据。

关键词：四履带张紧器；恒张力；AMESim；数学模型

脐带缆作为水下控制的关键组成部分，是连接上部设施和水下生产系统之间的“神经和生命线”，已成功地应用到浅水、深水和超深水域[1-2]；海洋柔性管道与脐带缆铺设技术在油气集输和水下生产中的作用变得越来越重要[3-7]。为了提高我国在深海管道与缆线的铺设能力，由中海油深海开发有限公司牵头承担了国家“十二五”科技重大专项“南海深水油气开发示范工程”项目。为配合荔湾3-1气田工程设计、建造、安装技术的实施，研制出一种具有自主知识产权的深水脐带缆铺设用四履带张紧器。

目前，国外在四履带张紧器的研制上已较成熟，工程上已有广泛应用；国内在四履带张紧器的总体方案、结构计算、液压系统、夹紧油缸系统的研究已经做了大量工作，而对张紧器的恒张力控制系统的研究还较少。在四履带张紧器的研制过程中，利用AMESim仿真平台建立四履带张紧器仿真系统模型，包含机械系统部分建模和恒张力控制系统部分建模，验证恒张力控制算法的有效性，同时通过仿真模型研究张紧器在不同深度的海域作业时缆绳张力的变化规律，进而对恒张力控制系统在不同工况下的PID参数设置提出建议，也为进一步研究PID自适应控制算法提供分析数据。

1四履带张紧器工作原理

四履带张紧器总体结构如图1所示。主要由履带总成、上履带翻转机构、履带框架总成及底座总成组成。履带总成通过四组液压缸推动对脐带缆进行夹紧和张开动作；通过变频电机驱动履带，实现对脐带缆的收放[8-9]。

在铺设管道之前，各条履带在液压缸的驱动下沿导轨向中心运动夹紧管道，通过位移传感器和压力传感器实时监测液压缸的行程和工作压力，保证管道在中心夹紧，并进行恒压力控制。同时每条履带带有悬浮液压缸，用来补偿管道外径的变化，保证履带有效接触面积。张紧器通过控制履带对管道的夹紧力和履带的正反向驱动，自动实现恒张力条件下管道沿船舶航迹铺设，同时可根据船舶和海上环境状态，自动实现收放管道工作。

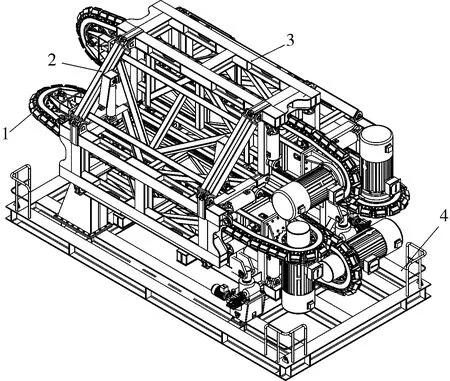
1—履带总成；2—上履带翻转机构；3—履带框架总成；4—底座总成。

由于管线终端尺寸较大，需将上框架履带总成打开，沿轴向方向将管线牵引至张紧器履带总成之间，再将上框架履带总成闭合。

2恒张力控制数学模型

四履带张紧器的恒张力控制系统，是张紧器电气控制系统的关键部分。在海底管线铺设过程中，由于海洋工况的复杂性，铺设的管线所受的张力为非线性，数学模型存在不确定性，简单采用单闭环控制策略，不能满足实际要求，控制精度不好。由于铺管(缆)船具有大惯量、速度变化率慢的特点，张紧器固定安装在铺管(缆)船上，因此张紧器履带驱动系统的恒张力控制策略可以利用此特点。在张紧器的设计中，履带驱动系统恒张力控制策略采用静态前馈-串级反馈控制策略，控制原理如图2所示。

图2　张紧器恒张力控制原理

在恒张力控制系统中通过设定管线张力值，进行静态前馈函数W1(0)得到运算值A；通过检测管线张力的测力传感器与设定铺设张力值的差值，进行PID函数W2(s)得到运算值B；通过测速编码器检测出的铺设速度值，进行PID函数W3(s)得到运算值C；将这三个运算值迭加后输送给变频器驱动变频电机。

在张紧器的机械结构和传动形式确定后，其固有的机械损失与时间因子无关。通过对装备进行静态标定检测，得出装备的补偿信号大小，固有机械损失补偿认为在两两标定值之间的数据是线性比例特性，故W1(0)为

A=W1(0)=Yn-1+

(1)

式中：Xn、Xn-1为实际设定张力值在标定时的上、下张力值；Yn、Yn-1标定时的上、下张力值对应的补偿信号值；F0为实际设定张力值。

在函数W2(s)和W3(s)的选择上，考虑PID调节器有典型的结构，参数调整方便，程序设计简单，计算工作量小，各参数具有明确的物理意义，并且能得到比较满意的效果。因此函数W2(s)和W3(s)采用PID控制函数。

(2)

(3)

式中：KP2，KP3为比例系数；Ti2，Ti3为积分时间常数；Td2，Td3为微分时间常数。

3基于AMESim张紧器恒张力控制建模

3.1仿真模型建立

采用AMESim信号库和机械库搭建四履带张紧器的履带传输的恒张力控制系统模型如图3所示。

图3　张紧器恒张力控制系统模型

张紧器履带恒张力系统仿真模型由静态前馈控制、张力PID反馈控制、速度PID反馈控制、机械系统和铺设管线模型5个子模型组成。

在系统张力和速度PID反馈控制模型中，考虑PLC的扫描周期为0.1 s，而AMESim模型仿真步长至少在0.01 s以下才能求解到比较好的收敛曲线，因此要加入过滤算法和采样开关来保持两者计算频率的一致性，过滤算法为

(4)

式中：Zn为过滤算法第n次输出值；Zn-1为过滤算法第n-1次输出值；Z为传感器进行模数转换后输出值；T为PLC循环扫描时间；N为过滤周期。

铺设管线模型是整个仿真系统重要的子模型之一，由于目前还没有实际铺管船舶在管线铺设过程中的载荷谱数据，而建立上千米长的管线多体动力学模型数据量非常庞大，很可能无法计算或收敛，因此需要建立管线的力学等效模型来进行仿真[10]。铺管船运行速度和管线铺设速度的不同是引起管线张力变化的根本原因，其过程与弹簧两端加载不同运动速度而引起弹力变化的过程类似，铺管船自身吨位大小的变化、铺管海域深浅的变化、铺管长度的变化等诸多因素会影响管线张力速度的变化率，而这些因素的影响结果都可以通过弹簧阻尼系统的刚度变化来体现。故本文采用变刚度阻尼弹簧系统来等效模拟铺设管线，在不同深度的海域采用不同刚度、阻尼的弹簧系统来代替铺设管线的动力学模型。为了简化仿真模型，海浪等对铺管过程的影响在后续研究中再做进一步分析。

3.2仿真参数设定

根据设计要求，张紧器的总铺设张力为850 kN，则每条履带提供的张力为212.5 kN，最大铺设速度为0.34 m/s，据此可以选定减速机及电机参数。张力和速度PID反馈控制模型中，除了设定常规PID参数外，还需要设置PLC的循环扫描周期、静带(死区)值等，模型仿真参数设置如表1所示。

表1　模型仿真参数

4试验及仿真结果分析

4.1试验与仿真数据比对

仿真模型中变刚度弹簧阻尼系统参数设置是整个仿真模型最关键的问题，由于管线铺设过程和工作环境复杂多变性，通过理论计算方法获得其等效刚度和阻尼非常困难，本文采用管线铺设试验数据来标定仿真模型的方法进行设定。具体过程为：首先在一定条件下进行管线铺设试验，得到恒张力控制曲线；然后将仿真条件设定与试验条件保持一致，同时不断调整弹簧系统的刚度和阻尼值，直至仿真得到的恒张力控制曲线与试验得到曲线近似一致，此时得到的刚度和阻尼值即认定为管线的力学等效模型设定值。

试验采用天津市精研工程机械传动有限公司研制的150 kN电驱动式张紧器，具备25～250 mm电缆铺设功能，模拟海上施工过程进行张紧器停、收、放、停运动状态下恒张力控制试验，如图4所示。通过计算机测试系统采集实际张力值和设定张力值，测量结果如图5所示。

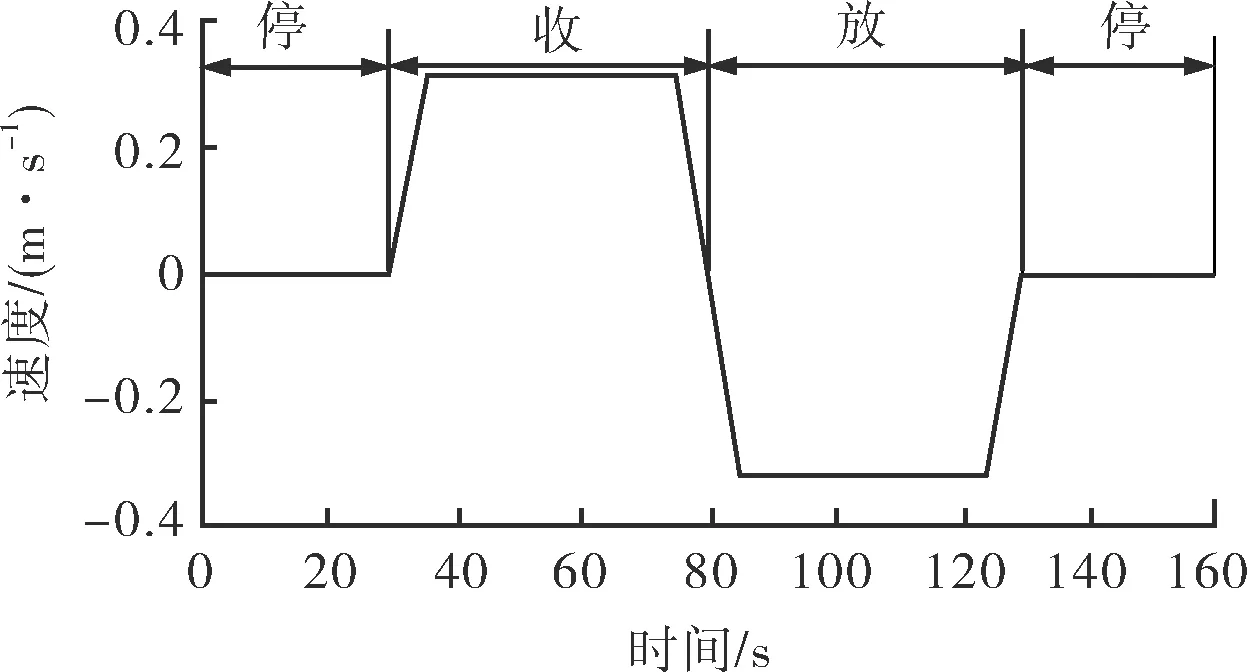
图4　工程船运行速度模拟

图5　试验测试的恒张力控制曲线

相同的管线铺设条件下仿真模型得到的恒张力控制曲线如图6所示，仿真参数设定如表2所示。

图6　基准工况的张力控制曲线

管线刚度k/(N·m-1)2.0×106管线阻尼c/(N·(m·s-1)-1)2.0×105过滤周期N/ms100张力PID控制增益Pf80速度PID反馈增益Pv253.2静带宽度w/%1

由图5～6可知，试验和仿真得到的恒张力曲线调整过程非常相近，超调量均为15 kN左右，但经过2～3次动态调整均很快稳定在设定值附近。定义此仿真曲线下为基准工况，其管道等效刚度、阻尼值即为表2中的数值。为了减少试验次数，根据基准工况的数据，利用仿真模型来进一步研究张紧器在不同海域下工作时PID控制和速度反馈的参数调整趋势。

4.2仿真数据分析

根据实际海底管线铺设情况可知，在浅海区铺设管线时，由于海水深度较浅并且管线总长度很短，管线的刚度很大而阻尼很小；而在深海铺设时，则恰恰相反，管线长达上千米，管线具有很好的柔性，刚度相对较小而阻尼较大。故采用低刚度大阻尼的弹簧系统模拟深海作业工况的管线，高刚度小阻尼的弹簧系统模拟浅海作业工况的管线，由于不同海域下管线的等效刚度需要后期实际铺管作业时才能测定，当前仿真模型各工况以经过试验标定的工况1作为基准工况，然后刚度、阻尼按一定倍数增减进行设定，如表3所示。

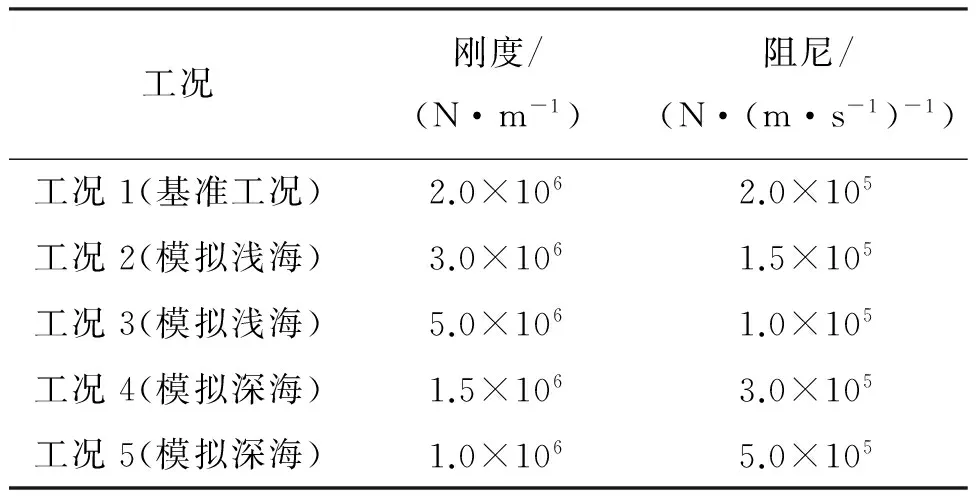
表3　仿真工况参数设置

相对于工况1，工况2、3模拟浅海作业，刚度增大为工况1的1.5倍、2.5倍，阻尼减小为3/4、1/2，其仿真控制参数调整结果如表4所示，张力控制曲线如图7所示。

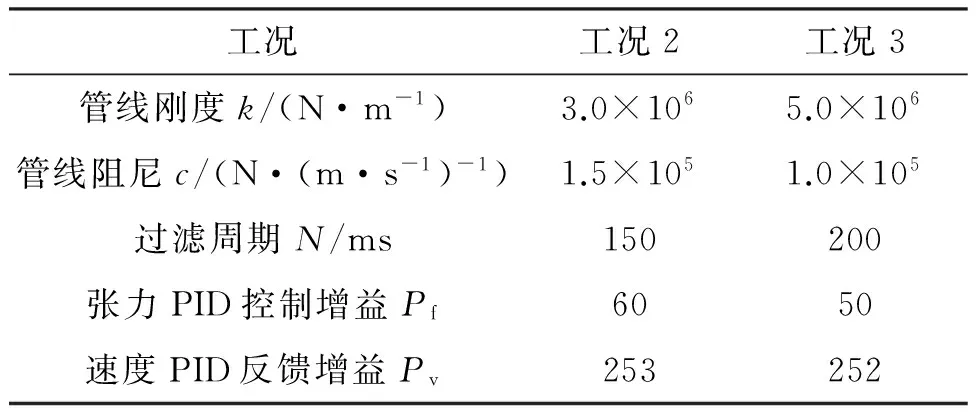
表4　工况2、3仿真参数设置

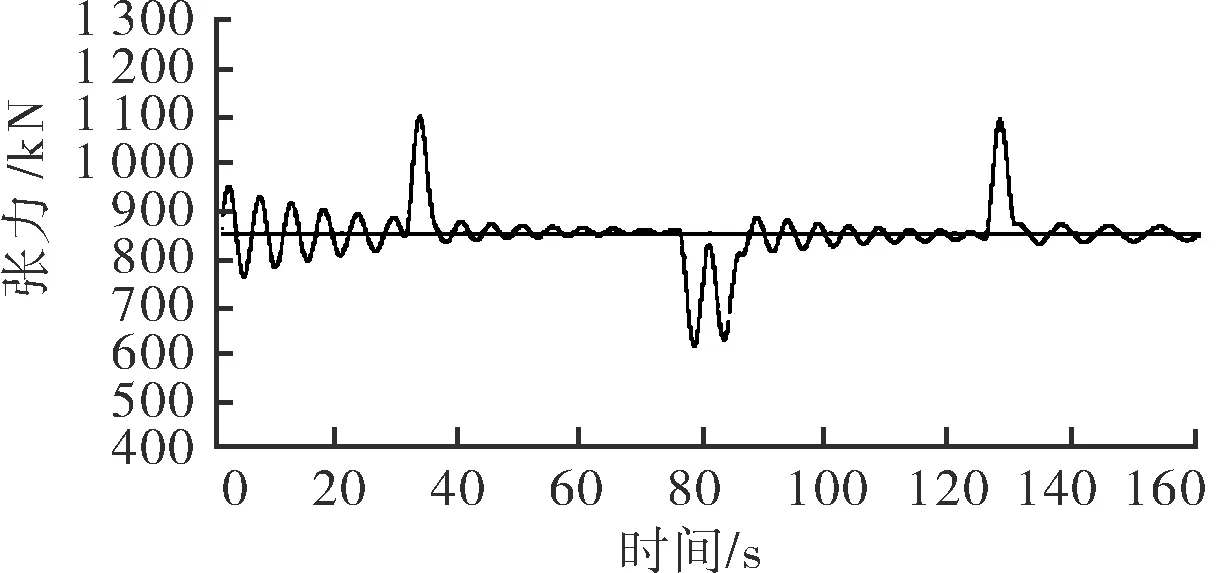
a　工况2

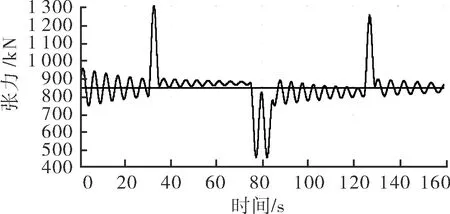
b　工况3

由图7、表4可知，随着管线刚度的增大和阻尼的减小，管线的张力在动态调整阶段超调量增大、振荡频率增大、稳定到张力设定值的时间增长。为了将管线张力响应曲线调整为工况1的状态，通过增加管线张力滤波周期来降低张力振荡频率，使其调整过程变得比较缓和；通过减小张力PID参数Pf来减小超调量；而速度PID反馈参数Pv主要影响系统的稳态值，降低Pv系统的响应速度加快，但是稳态误差增大。此外，过滤周期N的设定对系统响应影响很大，随着N增大，张力振荡频率会降低，张力调整过程变缓，稳定到设定值时间加长，系统的稳定性较好；但是滤波周期较大时，滤波算法会滤掉张力瞬态峰值，致使管线张力较大时因得不到调整而产生较大的瞬时超调。

相对于工况1，工况4、5分别将刚度降为3/4、1/2，阻尼增加为1.5倍、2.5倍，其控制参数调整结果如表5所示，控制参数调整过程如图8所示。

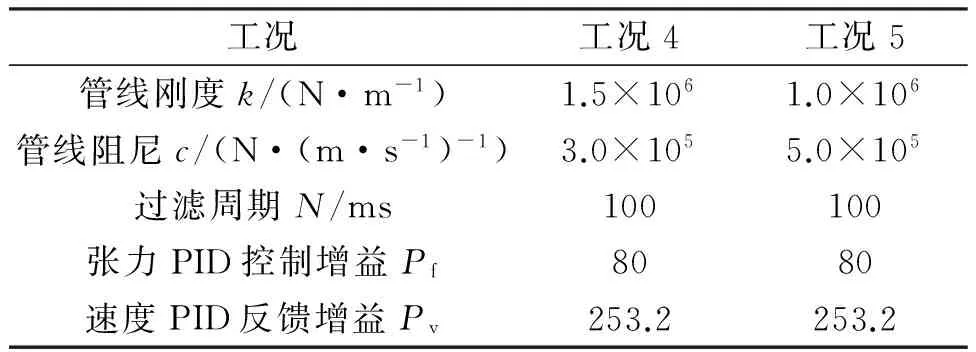
表5　工况4、5仿真参数设置

a　工况4

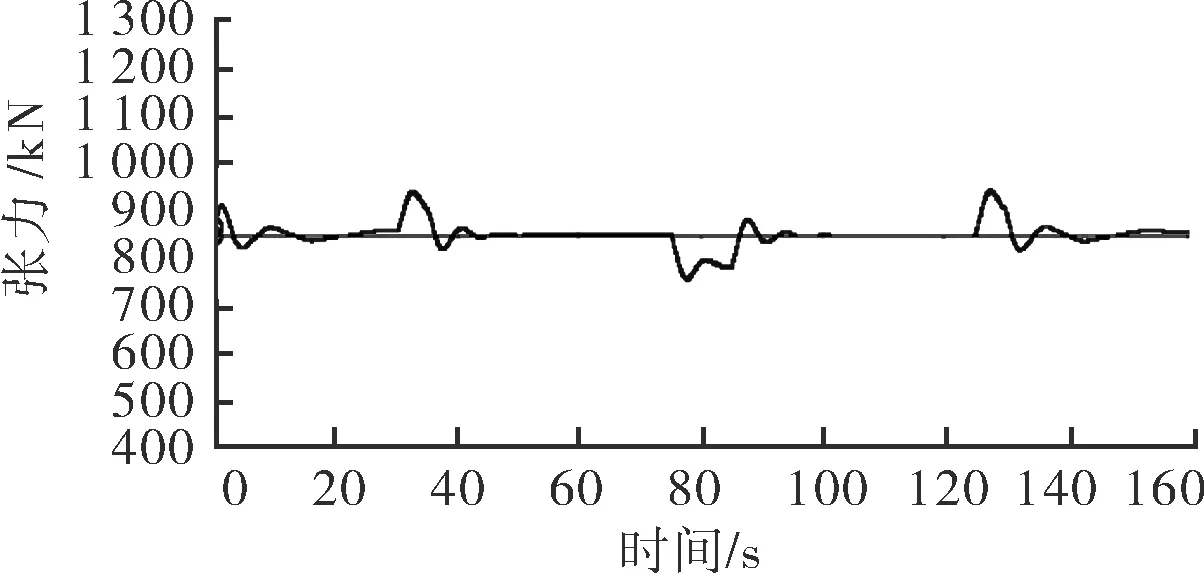
b　工况5

由图8、表5可知，随着管线刚度的减小和阻尼的增大，张力超调量降低，振荡频率降低，管线张力很快稳定在设定值，系统具有很好的稳定性，因为此时管线刚度低柔性好，故当船速变化时张力的变化不再剧烈。

将上述各个工况按照管道刚度由低到高排序，可以得到控制参数的调整趋势，即随着管道刚度的增大和阻尼的减小，增加过滤周期、降低PID控制增益、速度反馈增益能得到较好的张力响应曲线。

5结论

1)张紧器在浅海区域作业时管线具有较高的刚度和较小的阻尼；在深海区域作业时管线具有较低的刚度和较大的阻尼。

2)当张紧器在浅海作业时，随着管线刚度的增加，恒张力控制系统瞬态响应超调量加大，系统振荡频率明显增大，建议增大传感器数值过滤算法的过滤周期，使系统响应趋于缓和，减小系统振荡，增强系统的稳定性，但过大的过滤周期会产生较大的瞬时超调量；减小张力PID控制参数能够降低系统超调量，但会增加稳定时间；降低速度PID反馈控制参数也可增加系统的稳定性，但系统稳态误差会增大。

3)张紧器在深海作业时，随着管线刚度的降低，柔顺性变好，因此管线张力对母船速度变化敏感度降低；在一定范围内浅海区域控制系统参数也适用于深海区，即使控制参数不做调整也能得到较好的恒张力控制曲线。

4)仿真模型中管线模型采用等效刚度阻尼弹簧系统替代，该方法能够模拟管线的刚度特性，但忽略了管线的空间结构，后期研究应对管线结构进行离散化，建立等效的多自由度系统力学模型。

参考文献：

[1]张俊亮，刘文利，陈翠和，等.深水铺管船用张紧器液压夹紧系统建模与仿真[J].系统仿真学报，2010，22(2)：521-527.

[2]郭宏，屈衍，李博，等.国内外脐带缆技术研究现状及在我国的应用展望[J].中国海上油气，2012(2)：74-78.

[3]孙亮，张仕民，林立，等.海洋铺管船用张紧器的总体设计[J].石油机械，2008，36(8)：36-38.

[4]Zhang Junliang，Lin Li，Zhang Shimin.A Tensioner System for a DeepwaterPipelaying Vessel[C]// International Conference of Measuring Technology and Mechatronics Automation，2009：36-39.

[5]孙晶晶，刘培林，段梦兰，等.深水脐带缆安装技术发展现状与趋势[J].石油矿场机械，2011，40(12)：1-5.

[6]郭志平，李冠孚，刘仕超，等，四履带式海洋船用脐带缆张紧器设计[J].机械设计与制造，2013(8)：266-272.

[7]张宏，李志刚，赵宏林，等.深水海底管道铺管设备技术现状与国产化设想[J].石油机械，2008，36(9)：201-204.

[8]于博泉.深水脐带缆四履带张紧器结构设计与关键技术研究[D].哈尔滨：哈尔滨工程大学，2012.

[9]郭炜.85吨深海船用脐带缆张紧器设计与履带系统动力学分析[D].呼和浩特：内蒙古工程大学，2013.

[10]龚顺风，何勇，周俊，等.深水海底管道S型铺设参数敏感性分析[J].海洋工程，2009(11)：87-95.

Modeling and Simulation of the Constant Tension Control of the Four-track Tensioner

WAN Jianbo1，WANG Fushan2，WANG Hailing2，ZHOU Junfeng1，LI Huailiang3，WANG Hui1，WANG Dongfeng1

(1.TianjinJingyanConstructionMachineryTransmissionCo.，Ltd.，Tianjin300409，China；2.TianjinResearchInstituteofConstructionMachinery，Tianjin300409，China；3.OffshoreOilEngineeringCo.，Ltd.，Tianjin300451，China)

Abstract：The four-track tensioner is the key equipment in the installation system of deep-water umbilical cable，the constant tension control technology is the core of tensioner.The mathematical model of constant tension for four-track tensioner was obtained through analysis of the system of constant tension for tensioner.The simulation model of constant tension for four-track tensioner was established on the basis of the AMESim software，the effectiveness of constant tension control was verified，and the rule of constant tension diameters at the tensioner working on different sea conditions was studied.The analysis of data was obtained for studying the PID adaptive control algorithm.

Keywords：four-track tensioner；constant tension；ASMESim；mathematical model

文章编号：1001-3482(2016)06-0026-06

收稿日期：2015-12-02

基金项目：国家科技重大专项子项目 “脐带缆安装系统关键部件(A&R绞车)研制”(2011ZX05056-003-07)；天津市科技计划项目“恒张力控制技术研究与装备产业化”(14ZCDZGX00069)

作者简介：万箭波(1981-)，男，江西南昌人，高级工程师，主要从事机电设备及其控制系统研发，E-mail：wanjbo@jycmt.com。

中图分类号：TE952

文献标识码：A

doi：10.3969/j.issn.1001-3482.2016.06.006