基于贪心优化策略的网格排布算法
2016-07-19娄自婷张亚萍
娄自婷 张亚萍


摘要:针对由存储带宽和数据访问速度导致的复杂数据集绘制性能低下等问题,提出了一种基于贪心优化策略的三角形排布算法,通过对绘制数据集进行重排以改善数据的空间局部性和时间局部性。该算法首先将顶点分为三类,根据改进的代价函数选择代价度量最小的顶点作为活动顶点;然后绘制(即输出)其所有未绘制的邻接三角形,并将相邻顶点压入缓存,算法迭代执行直到所有顶点的邻接三角形都绘制完成,得到重新排列后的三角形序列。实验结果表明,该算法不仅具备较高的顶点缓存命中率,还提高了渲染速度,减少了排序的时间,有效地解决了图形处理器的处理速度不断提升而数据访问速度严重滞后的问题。
关键词:
缓存优化;网格排布;贪心优化策略;平均缓存失配率;三维网格模型
中图分类号: TP391.41 文献标志码:A
0引言
尽管近年来中央处理器(Central Processing Unit, CPU)与图形处理器(Graphics Processing Unit, GPU)的处理能力都有了很大的提升,但复杂数据集的绘制性能问题仍然存在,这主要是由于存储带宽和数据访问速度的增长远落后于处理能力的增长,数据的输入输出成为大规模数据处理最主要的瓶颈。为此,现代计算机系统大量采用了缓存机制,使用小容量的高速存储器为大容量的低速存储器提供缓存。为了充分利用缓存机制,数据应该有良好的局部性(locality)。局部性有两种基本形式:空间局部性(spatial locality)与时间局部性(temporal locality)。空间局部性表示与当前访问的数据单元邻近的数据单元很可能会被访问。时间局部性表示如果一个数据单元正在被访问,那在近期它很可能会被再次访问[1]。
为了提高CPU和GPU之间的数据交换速度,减轻顶点读取时的带宽要求,GPU采用顶点缓存机制与纹理缓存机制避免重复的顶点计算以提高缓存性能[2],目前已有多种优化纹理缓存访问效率的算法[3],而提高顶点缓存访问效率的算法屈指可数。顶点缓存的访问性能通常用平均缓存失配率(Average Cache Miss Rate, ACMR)来衡量,定义为绘制每个三角形的平均缓存失配次数,即缓存的总失配次数与总访问次数之比,ACMR的取值范围为[0.5,3.0],因为每个顶点至少失配一次,至多失配三次。需要注意的是,ACMR无法达到最小值,主要是因为顶点缓存区容量的限制。若顶点缓存区可以装下所有顶点,则以任何方式组织的三角形都可以使ACMR接近于0.5,但是缓存容量很小,很难装下所有的顶点,假设缓存容量为k,三角形顶点个数为n,k往往小于n,在理想情况下ACMR可以达到的最小值为k/2(k-1)=0.5+Ω(1/k),其中Ω(1/k)是1/k的线性函数[4]。此外,网格的形状也会导致ACMR额外的开销,因此要提高顶点缓存访问效率,需降低ACMR值,进行缓存优化。
1网格排布优化
缓存优化技术除了与硬件性能有直接关系,还与数据访问方式和数据排列方式有关。针对后者,设计缓存优化算法,通过重排技术来提高缓存访问性能。重排技术包括计算重排与数据重排[5]:1)计算重排,即根据重新排列指令顺序,提高访问相同数据单元指令的局部性,通常由编译器对应用程序编译后的指令序列进行重排来完成,对于指令,重新组织程序而不影响程序的正确性;2)数据重排,即根据指令对数据单元的访问方式求解出缓存连贯的数据排布,由应用程序直接对数据进行重排来完成,通过优化改善数据的空间局部性和时间局部性。
目前基于网格排布的缓存优化技术(以下简称网格排布优化技术)是计算机图形学与可视化领域的重点研究方向之一,该技术基于数据重排。根据求解技术手段的不同,网格排布优化技术可分为基于优化策略、基于空间填充曲线和基于谱序列三类[1];根据网格描述方式的不同,可分为基于三角形、基于三角形条带、基于三角形扇,每种描述方式又可分为索引形式和三角形形式[6]。因为索引形式只需少量数据,传输代价小,使之成为目前使用最为普遍的方式,但顶点随机读取也带来了ACMR的增加,因此许多研究者提出对网格图元的存储顺序进行重新排布,可以减小ACMR,降低顶点处理的运算量,提高渲染速度。
Hoppe[2]提出了基于贪心优化策略的条带算法,沿着逆时针方向生成条带,进行三角形条带合并,在合并的过程中不断检测预期的ACMR,以此降低顶点缓存失配率。Bogomjakov等[7]提出了基于空间填充曲线的非条带算法,该算法使用图划分软件包Metis[8]将网格分成多个三角形簇,保证每个簇内三角形序列的ACMR最优,从而形成整个网格的ACMR最优化。Lin等[9]也提出了一种基于优化策略的三角形绘制序列生成算法,应用启发式条件对网格顶点进行全局搜索,同样可以得到很低的ACMR。Sander等[10]对Lin等[9]算法进行了改进,该算法只在上一个输出的三角形环周围进行启发式搜索。Nehab等[11]提出了一种基于优化策略的多功能三角形序列重排算法,该算法不仅可以减小ACMR,还可以减小图元的重绘率(OVerdraw Ratio, OVR)。除了上述几种常见算法外,Yoon等[12]提出了一种在未知缓存参数情况下的网格排布优化算法,在不用修改应用程序的条件下,该算法对基于视点的绘制、碰撞检测和等值线提取等几何应用达到了2~20倍的加速比。Liu等 [13]提出了一种基于图距离函数的谱序列算法,该算法先为图中的任意点对计算一个距离值,然后计算图中的一个高维嵌入,使在嵌入中顶点的距离关系和最先计算的图的距离函数一致,最后将嵌入中的点投影到一个向量上,并对其进行排序。Bartholdi等 [14]提出了一种基于空间填充曲线的三角网格多分辨率索引方法。Limper等[15]提出了一种隔行扫描的网格排布优化算法,该算法在绘制过程中会对ACMR产生负面的影响,也影响了整体的渲染性能。
相对于国外,国内研究该领域的较少,有熊华[1]、石教英[16]提出的基于三角形排布的缓存优化算法,该算法的核心思想是对于与当前缓存中顶点邻接而本身不在缓存中的顶点,如果将该顶点压入缓存中,并且不再压入其他顶点时,计算可以直接输出最多三角形数量的顶点作为当前输出顶点,将其压入缓存中,并将可输出的三角形全部输出。该算法主要优点在于计算速度快,ACMR接近于Lin等[9]提出的算法。陈思远等[4]提出的基于三角形条带的网格排布优化算法,目的在于降低运算时间复杂度,并且使ACMR接近于Hoppe与Lin等[9]算法。算法的基本思想是顶点缓存中驻留的顶点为后续的三角形条带提供了公共边,沿着这些公共边将三角形以条带为单位进行遍历,可以得到理想的ACMR值,并且在遍历衍生条带的过程中到达网格的边界时,需要选择合适的位置重新初始化新的条带,在此期间需要考虑减少重新初始化时造成的ACMR开销。秦爱红等[6]提出的基于混合模式的缓存优化算法,该算法的核心思想是采用优化求解传输代价方程,通过精确地模拟缓存状态变化得到理想的缓存命中率,启用后进先用的数据引用方式重新定义优化求解传输代价方程,使三角形条带同时兼顾顺时针和逆时针增长方向,极大地提高了三角形条带内部顶点的重用性,使之在任意顶点缓存中可有效地提高顶点缓存命中率。陆扬[17]提出的基于均匀网格的预处理算法,该算法首先将网格分为大小尽可能相等的多块子网格,然后采用Sander等[10]提出的算法对顶点进行重排序,该算法对不同拓扑特征、不同网格规模的模型能产生较低的ACMR。
2基于贪心优化策略的网格排布算法
2.1算法分析比较
本文给出了8种常见算法的平均ACMR值,如图1所示。由图1可以看出,原先这部分用的人名表示的算法,比较乱,现统一改为文献几算法,核实。正确文献[9]算法与文献[2]算法平均ACMR值最低,文献[10]算法、文献[11]算法与文献[1] 算法略高于文献[9]算法与文献[2]算法,其余算法优化效果较差。
如图2所示为PLY(Polygon File Format)文件格式,主要用以存储立体扫描结果的三维数值,透过多边形面片的集合扫描三维物体,有纯文字(ASCII)与二元码(binary)两种版本,其差异在于存储时是否以ASCII编码表示元素资讯。该模型表示与其他格式相比较为简单。表1给出了它们的顶点数量、三角形数量和数据量大小,其中数据量是指ASCII格式的网格文件的大小。
表2给出了五个测试模型使用文献[9]算法进行网格排布优化的ACMR值和执行时间,文中的实验数据都在Intel Core i72600 @ 3.40GHz,NVIDIA GeForce GTX 460(1GB) ,4GB内存的实验环境中测得。从表2中可以看出,该算法在缓存为12时得到的ACMR值最优,虽然优化时间也最优,但还是相对较长,与模型大小、缓存大小成正比关系。所以本文通过改进文献[9]算法(LinSort),使ACMR更优,同时减少算法的执行时间。
2.2基于贪心优化策略的三角形排布优化算法
为了保证算法效率与优化效果,本文对LinSort进行了改进,提出一种基于贪心优化策略的三角形排布优化算法。该算法的核心思想是将顶点定义为以下3类:1)白色表示顶点不在缓存中。与该顶点邻接的一部分或所有三角形都没有被绘制,因此需要在绘制时将顶点放入缓存。2)灰色表示顶点在缓存中。3)黑色表示与该顶点邻接的所有三角形都已经被绘制,该顶点可能在也可能不在缓存中。一旦该顶点离开缓存,在绘制时将不再需要该顶点,也不需要将其压入缓存中。
在每次迭代执行算法时,选择一个灰色或者白色(缓存为空时)顶点作为活动顶点,将该顶点的所有未绘制的邻接三角形顶点压入缓存并进行绘制。一旦顶点连接的所有邻接三角形都已经被绘制,将该顶点标记为黑色。该算法的基本思想是在绘制期间保证算法局部性,即减少每一个顶点的缓存失配次数(缓存失配率),因此需要在每个绘制阶段决定用哪个顶点作为活动顶点,这也决定了最终呈现的绘制序列。
为了达到最优绘制效率,减小缓存失配率,赋予每个顶点v一个代价度量,用C(v)表示。在选择当前顶点时,根据代价函数选择代价度量最小的顶点,在LinSort [9]中,代价函数表示为:
C(v)=k1C1(v)+其他K1与K3与后面项全是乘,只有k2与C2是除,核实是否正确?正确k2/C2(v)+k3C3(v)
(1)
其中:C1(v)表示绘制完顶点v所有未绘制的邻接三角形时,需要压入缓存的顶点数;C2(v)表示在顶点v标记为黑色之前可以绘制的三角形数量;C3(v)表示顶点v标记为黑色时在缓存中的位置;k1、k2、k3为权重系数,也是影响ACMR的重要因素。在LinSort [9]中,对任意的模型没有给出特定的权重,而是凭直觉给出了经验值,当K=12、k1=1、k2=0.5、k3=1.3时得到的ACMR最低。设置这一组经验值是因为三角形数通常是顶点数的2倍,为了保证C1与C2的一致性,设置k1≈2k2,k3应接近于k1与k2,表3即在该条件下测得。而经过多次实验,发现文献[9]给出的经验值虽然能得到最优的ACMR值,但是在K=12、k1=1保持不变的情况下,设置k2与k3的值,k2=0.5~6.5、k3=0.1~2.7的范围内得到的ACMR偏差都在0.1内,但是对于先进先出(First Input First Output, FIFO)置换策略,需要设置k3值大于1,因为在此条件下,才能优先考虑先进入缓存的顶点,防止顶点再次压入缓存。
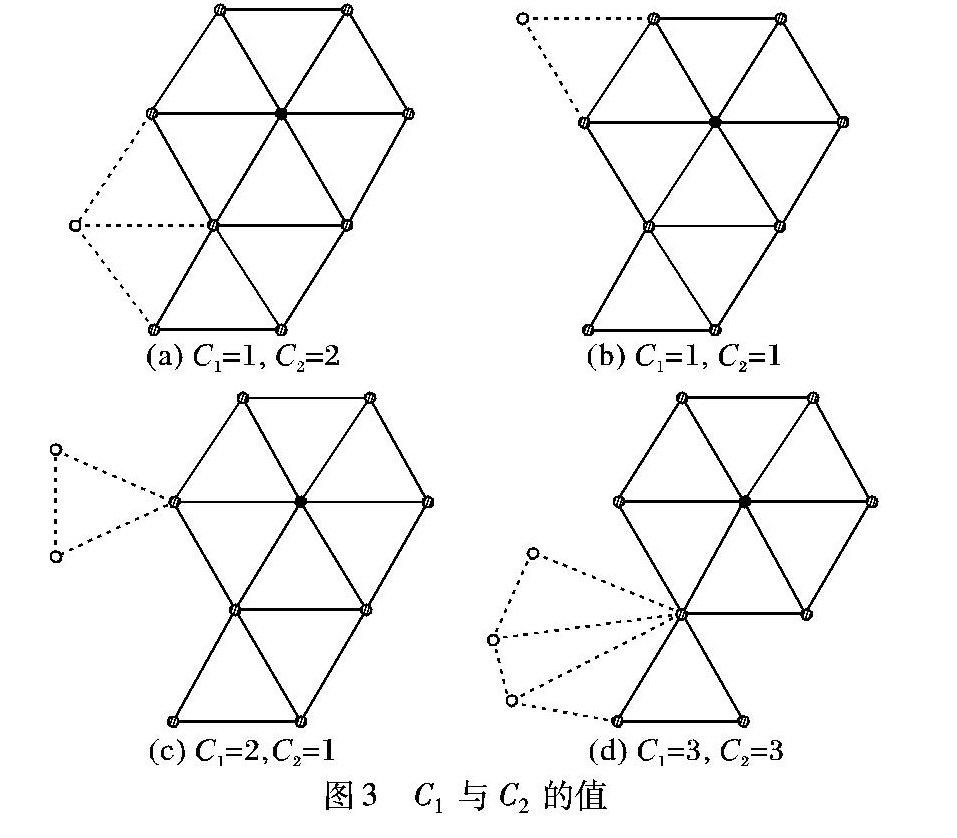
如图3所示,实心圆点表示该顶点已经在缓存中,空心圆点表示顶点还未绘制,C1与C2分别表示需要压入的顶点数与可以绘制的三角形数,同C1(v)与C2(v)。若根据文献[9]提出的代价函数选择最小代价度量的顶点作为当前活动顶点,选择K=12、k1=1、k2=0.5、k3=1.3,则图3(a)为1.25+1.3C3(v),图3(b)为1.5+1.3C3(v),图3(c)为2.5+1.3C3(v),图3(d)为3.17+1.3 C3(v)。根据当前缓存情况及代价函数,本文选择图3(a)进行绘制,可使本次操作的失配率最低,从而降低总的ACMR。
当只有图3(c)~(d)两种情况时,根据最小代价度量函数,选择图3(c)进行绘制,但是为保证ACMR最优,对与当前缓存中顶点邻接而不在缓存中的顶点,在压入该顶点到缓存中时,需要选择可输出三角形数最多的顶点。在图3(a)中,如果将空心圆点压入缓存中,可以输出两个三角形,平均缓存失配率为1/2;在图3(b)中,如果将空心圆点压入缓存中,可以输出一个三角形,平均缓存失配率为1;在图3(c)中,如果压入两个空心圆点到缓存中才能输出一个三角形,平均缓存失配率为2;在图3(d)中,如果压入三个空心圆点到缓存中可以输出三个三角形,平均缓存失配率为1。所以在只有图3(c)~(d)两种情况时,应该选择图3(d)才能使ACMR最优。故此,在Lin等[9]计算最小代价度量的代价函数基础上加上平均缓存失配率,即C1(v)/ C2(v),将改进的代价函数表示为:
C(v)=k1C1(v)+为什么别的项是乘,其他项是除,核实是否正确?正确k2/C2(v)+k3C3(v)+C1(v)/ C2(v)
(2)
根据改进的代价函数计算图3(c)~(d)的最小代价度量,得到图3(c)为4.5+1.3C3(v),图3(d)为4.17+1.3C3(v),前者大于后者,证实了选择图3(d)进行绘制可以得到更低的ACMR值。
下面给出了算法的伪码描述,其中V和F分别表示模型的顶点集和面集;M为FIFO缓存模型;Vw、Vg、Vb分别表示白色、灰色和黑色顶点集;Vg表示当前缓存区的顶点集;Foutput表示生成的三角形绘制序列。当Vg≠时,选择Vg中代价度量最小的顶点作为活动顶点vfocus,也就是vfocus =arg minv∈Vg C(v)。如果缓存为空,即Vg=,选择任意一个白色顶点作为活动顶点压入缓存,并标记为灰色。
Procedure KCacheReorder(V,F,M)。
程序前
1)
Initialization: Vw ← V, Vg ← , Vb ← , Foutput ←
2)
While | Vb |<| V|
/*iterate until all vertices turn into black*/
3)
if Vg=
/*buffer is empty*/
4)
vfocus ← any white vertex
5)
else
6)
vfocus ← minimum cost vertex in Vg
7)
F′(vfocus) ←{f∈F \ Foutput: vfocus is a vertex of f}
8)
for each f∈F′(vfocus)
9)
V′(f) ←{white vertex(es) of f}
10)
for each v∈V′(f)
11)
if | Vg|=K
/*buffer is full*/
12)
pop_one(M, Vg, f), v ← first vertex of Vg
13)
Push v: Vw ← Vw\{v}, Vg ← Vg∪{v}
14)
Output any renderable faces except f
15)
Output f : Foutput ← Foutput∪{f}
16)
Turn vfocusblack: Vb ← Vb∪{vfocus}
17)
这一句之前在16后面,为什么不单独列序号?排版时换了16、17、18三句,核实是否有误?都可以if Vg≠
18)
Vg ← Vg\{vfocus}
19)
Checking each v∈Vg for the possible turning black and leaving the buffer
程序后
2.3排布算法流程
首先给出该算法的相关数据结构:
程序前
typedef struct VertCachRec{
//顶点在缓存中的记录
unsigned int nVertIdx;
//顶点索引
byte bFlag;
//顶点标记
}VertCachRec;
typedef struct WhiteVertRec{
//白色顶点记录
unsigned int nVertIdx;
//白色顶点索引
WhiteVertRec* pNextRec;
//指向下一个白色顶点
}WhiteVertRec;
class CVertexConnRecord{
//顶点邻接的三角形记录
std::deque
byte m_bFlag;
//顶点标记
};
//顶点邻接的三角形记录
CVertexConnRecord* m_pVertexConnRec;
//白色顶点列表
WhiteVertRec** m_pWhiteVertHashMap;
//当前顶点缓存列表
std::deque
程序后
对于算法输入,采用三角形索引方式,每个三角形包含三个顶点索引。对于算法输出,内容与输入的序列一样,只是三角形的位置被重新排列。
下面是该算法的关键步骤:
1)提取三角形顶点信息,扫描三角形顶点列表,将顶点邻接的所有三角形索引压入顶点邻接的三角形记录的三角形索引列表中,建立三角形之间的连接关系。然后再次扫描顶点列表,计算每个顶点邻接的三角形数,若邻接三角形为0,表明该顶点为孤立顶点,标记为黑色顶点;否则将该顶点标记为白色顶点,创建白色顶点记录并将白色顶点压入白色顶点列表中。
2)初始化网格排布优化。此时的缓存为空,若白色顶点列表不为空,遍历白色顶点列表,选择任意一个白色顶点作为活动顶点,将白色顶点压入顶点缓存,并标记为灰色顶点。
3)选择活动顶点进行绘制。遍历缓存,分别计算缓存中当前顶点所有未绘制的邻接三角形,需要压入缓存的顶点数及当前在缓存中的位置,然后根据代价函数选择代价度量最小的灰色顶点作为活动顶点进行绘制。当一个顶点的所有邻接三角形都已经被绘制,则将该顶点标记为黑色。
对于需要压入缓存的顶点数,首先遍历顶点邻接三角形记录的三角形索引列表,得到当前顶点连接的三角形索引及三角形索引对应的所有顶点索引,判断这些邻接三角形顶点标记。若邻接三角形顶点标记为白色,则将该顶点从白色顶点列表中弹出,并压入缓存列表,将该顶点标记为灰色,从而得到最终需要压入缓存的顶点数。若FIFO顶点缓存已满,弹出缓存头部的顶点,将活动顶点未绘制的邻接三角形顶点压入顶点缓存。若缓存头部顶点的邻接三角形还未绘制完,则需要将该顶点再次标记为白色,压入白色顶点列表中,需要时再次压入缓存;若该顶点邻接的所有三角形都已经被绘制且该顶点已经标记为黑色顶点,则直接将该顶点弹出缓存,且不再需要压入缓存中。
4)若三角形全部顶点都标记为黑色,表明顶点已经全部绘制完,得到重新排列后的三角形绘制序列。
3实验结果与比较
表4给出了本文算法与LinSort[9]的优化结果,其中缓存大小为12,k1=1、k2=0.5、k3=1.3,可以看出,本文算法相对于LinSort[9],ACMR的值更低。图4(a)表示测试网格模型的原始网格排布,图4(b)表示模型优化后的网格排布,颜色深浅表示图元顺序前后位置。图5(a)~(b)分别表示模型进行三角形排布优化前及优化后的缓存失配结果,黑白印刷,彩色无法体现,请改成灰度描述。已核实黑色表示缓存失配,灰色表示缓存命中。
表5统计了五个测试模型在LinSort [9]和本文算法中的执行时间。从表4~5中可见,与LinSort [9]相比,本文算法的ACMR值降低了,优化算法时间也相对减少。分析其原因,主要是因为LinSort [9]在初始化网格时选择顶点邻接三角形最小的白色顶点作为活动顶点,而本文算法选择任意白色顶点作为活动顶点。在选择最小代价度量值时,不仅考虑邻接的未输出三角形数量、绘制完这些邻接三角形需要压入缓存的顶点数及顶点在缓存中的位置三个因素,还考虑了前两者的权重,因此在保证网格优化质量的同时减少了算法的执行时间。
为了考察模型大小及模型优化后的ACMR对渲染性能的影响,对上述5个模型在LinSort和本文算法下得到的优化结果进行模型交互绘制速率的测试,测试结果如表6所示。由表6中数据可知,模型交互绘制速率与模型大小非常接近于线性反比关系,模型交互绘制速率随着模型的增大而降低;单个模型交互绘制速率与ACMR值也成反比关系,模型交互绘制速率随着ACMR值的降低而提高。
4结语
在深入分析LinSort算法的基础上,本文提出了一种改进的基于贪心优化策略的网格排布算法。实验表明,该算法不仅具备更高的顶点缓存命中率,还提高了渲染速度,减少了排序的时间。具体而言,本文的基于贪心优化策略的网格排布优化算法具有以下特点:1)对输入网格模型拓扑结构没有要求,可以处理非条带三角形网格; 2)针对三角形序列直接进行重排,便于与其他算法和应用系统的集成; 3)代价度量与多个因素相关,优化质量高,计算速度快,但该算法只适用于100MB以下的网格模型,而对于大规模三维网格模型无法直接进行重排,并且本文时间复杂度还没有成数量级降低,所以接下来的工作主要针对大规模网格模型,采用网格分割算法将网格分割成多个子网格,然后对每一个子网格进行并行的缓存优化处理,使大规模三维网格模型能进行网格排布,并且在保证优化效果的同时大幅度提高算法执行速度。
参考文献:
[1]
熊华.面向并行环境的绘制加速技术研究[D].杭州:浙江大学,2008:71-80. (XIONG H. Research of rendering acceleration techniques for parallel environments [D]. Hangzhou: Zhejiang University, 2008: 71-80.)
[2]
HOPPE H. Optimization of mesh locality for transparent vertex caching [C]// SIGGRAPH99: Proceedings of the 26th Annual Conference on Computer Graphics and Interactive Techniques. New York: ACM, 1999: 269-276.
[3]
戴雪峰,熊汉江,龚健雅.一种三维城市模型多纹理自动合并方法[J].武汉大学学报:信息科学版,2015,40(3):347-352. (DAI X F, XIONG H J, GONG J Y. A multitexture automatic merging approach for the 3D city models [J]. Geomatics and Information Science of Wuhan University, 2015, 40(3): 347-352.)
[4]
陈思远,史广顺,王庆人.通过三角形strip衍生实现三维模型数据的渲染优化[J].计算机辅助设计与图形学学报,2009,21(8):1155-1163.(CHEN S Y, SHI G S, WAND Q R. Data optimization for 3D model rendering by triangle strip deriving [J]. Journal of ComputerAided Design & Computer Graphics, 2009, 21(8): 1155-1163.)
[5]
YOON SE, LINDSTROM P. Mesh layouts for blockbased caches [J]. IEEE Transactions on Visualization and Computer Graphics, 2006, 12(5): 1213-1220.
[6]
秦爱红,石教英.基于混合模式缓存优化的三角形条带化[J].计算机辅助设计与图形学学报,2011,23(6):1006-1012. (QIN A H, SHI J Y. Cachefriendly triangle strip generation based on hybrid model [J]. Journal of ComputerAided Design & Computer Graphics, 2011, 23(6): 1006-1012.)
[7]
BOGOMJAKOV A, GOTSMAN C. Universal rendering sequences for transparent vertex caching of progressive meshes [J]. Computer Graphics Forum, 2002, 21(2): 137-148.
[8]
KARYPIS G, KUMAR V. Multilevel kway partitioning scheme for irregular graphs [J]. Journal of Parallel and Distributed Computing, 1998, 48(1): 96-129.
[9]
LIN G, YU T P Y. An improved vertex caching scheme for 3D mesh rendering [J]. IEEE Transactions on Visualization and Computer Graphics, 2006, 12(4): 640-648.
[10]
SANDER P V, NEHAB D, BARCZAK J. Fast triangle reordering for vertex locality and reduced overdraw [J]. ACM Transactions on Graphics, 2007, 26(3): 89-97.
[11]
NEHAB D, BARCZAK J, SANDER P. Triangle order optimization for graphics hardware computation culling [C]// Proceeding of 2006 Symposium on Interactive 3D Graphics and Games. New York: ACM, 2006: 207-211.
[12]
YOON S, LINDSTROM P, PASCUCCI V, et al. Cacheoblivious mesh layouts [J]. ACM Transactions on Graphics, 2005, 24(3): 886-893.
[13]
LIU R, ZHANG H, VAN KAICK O. Spectral sequencing based on graph distance [C]// GMP 2006: Proceeding of the 4th International Conference on Geometric Modeling and Processing, LNCS 4077. Berlin: Springer, 2006: 632-638.
[14]
BARTHOLDI J J, GOLDSMAN P. Multiresolution indexing of triangulated irregular networks [J]. IEEE Transactions on Visualization and Computer Graphics, 2004, 10(4): 484-495.
[15]
LIMPER M, JUNG Y, BEHR J, et al. The POP buffer: rapid progressive clustering by geometry quantization [J]. Computer Graphics Forum, 2013, 32(7): 197-206.
[16]
石教英.分布并行图形绘制技术及其应用[M].北京:科学出版社,2010:189-274.(SHI J Y. Distributed Parallel Rendering Technique and Its Application [M]. Beijing: Science Press, 2010: 189-274.)
[17]
陆扬.基于CUDA的三角形并行处理[D].合肥:中国科学技术大学,2010:13-21. (LU Y. Parallel triangle processing with CUDA [D]. Hefei: University of Science and Technology of China, 2010: 13-21.)
