陆上风机圆形基础底板承载力计算方法研究

梅毕祥，杨 敏（同济大学 地下建筑与工程系，上海 200092）



陆上风机圆形基础底板承载力计算方法研究

梅毕祥，杨 敏
（同济大学 地下建筑与工程系，上海 200092）

摘要：不同于常规构筑物基础，陆上风机圆形基础具有受荷动力效应显著、截面尺寸大等特点。以常规构筑物圆板基础破坏模式为基础，使用极限平衡方法，对风机基础在主要破坏模式下的极限荷载进行了理论推导，开展了风机基础截面尺寸、径环向配筋量等参量的影响分析。分析表明，风机圆形基础的承载力由基础外悬挑扇形块破坏模式确定，其他破坏模式不起控制作用；烟囱规范的长悬挑圆形基础承载力计算公式不适用于风机基础设计；本文提出了风机圆形基础承载力的计算公式及相配套的设计建议，可望为风机基础规范的制定和基础工程设计提供有益参考。

关键词：陆上风机；圆形基础；破坏模式；承载力

引 言

国内外风电市场发展迅猛，但相关的风电技术标准却严重滞后，对于圆形基础底板的设计存在方法不统一的现象。欧洲标准化委员会发行的欧盟标准 2：混凝土结构设计［1］，规定圆形基础底板可采用正交配筋模式，但此模式无法适应非正交方向的受力特性。HENRIK SVENSSON［2］使用倒置梁法计算圆形基础底板弯矩和剪力，但此法存在无法确定

梁横截面方向承载力及配筋的缺点。水电水利规划设计总院组织编制的《风电机组地基基础设计规定》［3］，只对方形基础和方形承台桩基础的设计做了具体规定，而对于现在较流行的其他基础型式如圆形基础、圆形承台桩基础等设计均未做说明。CFD风力发电工程-机组塔架地基基础设计软件［4］，参照《烟囱设计规范》［5］推荐的板极限平衡法，此法计算基础承载力时与所选用的破坏模式相关，当选用的破坏模式不同，其数值也不同。与烟囱基础相比，陆上风机基础荷载动力效应显著，截面尺寸更大，两者破坏模式存在差异性。因此，有必要结合风机基础截面和荷载特性，深入研究圆形基础破坏模式及其承载力，以保证风机基础设计的安全性。

1 风机圆形基础的截面特性

圆形基础的破坏模式与其截面形状、悬挑几何条件及配筋情况等相关。风机基础的荷载动力效应显著，其截面特性不同于常规构筑物圆板基础。

烟囱作为常规构筑物，其圆板基础的截面计算示意如图1所示。

图1 圆板基础计算示意

在图1中， r1为外圆半径， r2为环壁外侧圆半径， r3为环壁内侧圆半径， rz为环壁底截面中心处圆半径，rz= （r2+ r3）/2，h1为外悬挑端部高度，h为悬挑根部高度，外悬挑端部厚度系数 γ= h1/h ，悬挑外形系数 α= r1/rz。

风机基础的截面计算示意如图2所示。

图2 风机圆形基础计算示意

相对于烟囱基础，风机基础截面具有如下特性：

1）悬挑长度上呈现“长悬臂，小内径”

随着风电单机容量和发电功率的不断增大，基顶承受巨大的偏心荷载，基底产生较大的不均匀土反力，为了满足风力发电机组结构的整体稳定性和地基强度条件，圆形基础基底面积增大；为了避免风机叶片与塔筒外壁之间的碰撞，保证风机正常运行，塔筒直径应满足最大限值要求，故具有 “长悬臂，小内径”特点。

就具体尺寸而言，一般情况下，烟囱圆板基础的悬挑外形系数α = 1.2～1.8［6］，当α ＞ 1.8时，认为基础外形不合理，一般不采用［5］。风机圆形基础常用外形的统计数据［2，4，7-8］表明，对于中型及中型以上风机圆形基础，α ≥ 2.5，已远远超过烟囱基础的数值。

2）基础板厚呈现“中间厚，四周薄，厚度不均匀”等特点

在现行烟囱规范中，圆板基础厚度基本保持不变。风机圆形基础由于其悬挑长度大，从降低工程造价的角度，将其径向弯矩为零的自由端板厚减小，将环壁或基座边缘处弯矩较大的底板变厚。当上部钢结构圆形塔架通过钢质套环固定于基顶时，基顶作用轴力、剪力、弯矩和扭矩等复杂内力。为了保证该连接部位的安全，工程上常将混凝土基座厚度加大，使得风机基础呈现“中间厚，四周薄，厚度不均匀” 等特点。

3）支座处钢质套环刚度对圆板转动的有效约束作用

在现行烟囱规范中，计算圆板基础承载力时，常假定底板为铰支支承于环壁处的悬挑板。对于风机圆形基础，不管上部结构为混凝土塔架或钢结构塔架，埋置于基顶的钢质套环均对基础底板的转动有一定的约束作用，相对于外悬挑板，该约束作用对内跨板的影响更显著，对内跨板的破坏模式产生一定的影响。

2 风机圆形基础的破坏模式

风机圆形基础和常规圆板基础的底板均为悬臂构件，常规圆板基础的破坏模式及其承载力研究成果对风机基础的承载力计算具有借鉴作用。

试验及理论分析表明，常规圆板的破坏模式除与悬挑的几何条件有关外，还取决于板厚及配筋情况。一般情况下，圆形板可能出现的破坏模式有六种［9］，见图3所示，假设图中基底压力竖直向下。

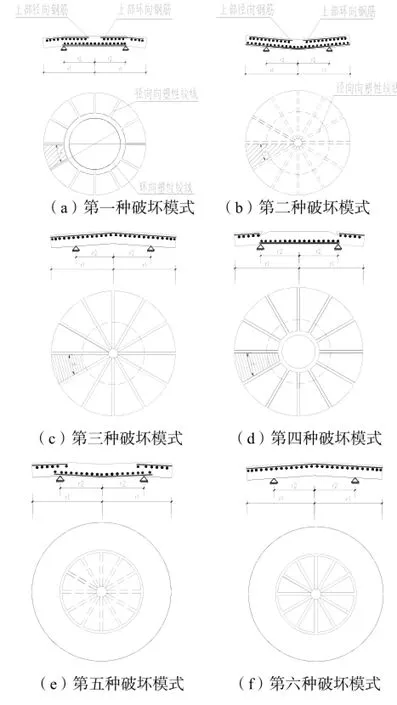
图3 简支悬挑圆板破坏模式

当圆形板悬挑较长，悬挑部分环向钢筋较强，而支座处径向钢筋和跨中上部环向钢筋较弱时，板可能发生第六种破坏模式。破坏时，除跨中上部产生通过圆心的放射向裂缝外，仅在支座处出现一道环向裂缝，此时，仅圆板跨中部分上凸（图3f）。

当上部径向钢筋在跨中切断过早时，圆板可能发生第四种破坏模式。破坏时，在圆板中央部分形成一道环向裂缝，并由此产生一束延长线通过圆心的放射向裂缝（图3d）。

就风机圆形基础而言，由于其悬挑尺寸较大，不会发生第二种和第五种破坏模式；实际工程中悬挑部位径向钢筋直接伸长至基础圆心附近，可控制不出现第四种破坏模式；相对于第一种和第六种破坏模式，第三种破坏模式不起控制作用；对板式基础工程中的常用外形而言，外悬挑的配筋主要由第一种破坏模式控制，支座内跨板的配筋主要由第六种破坏模式控制。因此，本文仅讨论风机圆形基础的第一种和第六种破坏模式及其相应的极限荷载大小。

3 风机圆形基础承载力计算

根据机动定理［10］，当结构的截面、配筋及混凝土强度等级相同时，在各种可能产生的破坏模式中，应选择极限荷载最小的破坏模式作为主控模式。本论文基于上述原理，使用极限平衡理论，考虑风机基础截面尺寸效应，对风机基础在主要破坏模式下的极限荷载进行了理论推导，并进行了参量分析。

3.1 基本假定

1） 假定基础的截面尺寸、钢筋和混凝土材料等级相同；

2） 假定基础配筋量已知且相同，并由第一种破坏模式控制确定；

3）基础发生破坏时，环向极限弯矩沿径向长度上均匀分布。

3.2 承载力计算

1）第一种破坏模式

从图3（a）中，取支座以外中心角为dφ的截扇形小块为隔离体，其上作用均载 p1，支座处单位长度上的环向极限弯矩 M，支座处单位长度上的径向极限弯矩 MrB，弯矩符号规定板下部受拉为正，内外力对T-T轴（图4a）的力矩平衡条件为：

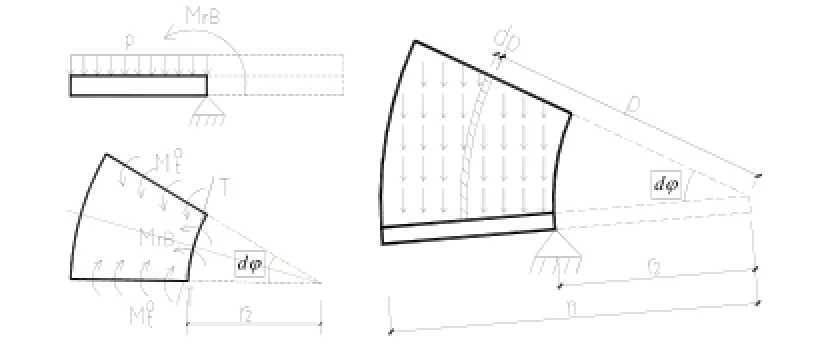
图4 悬挑截扇形小块隔离体

式中： mB为均载 p1对支座处单位弧长上的外力矩，从图（4b）可知：

将（2）式代入（1）式，并注意到环支座处径、环 向 弯 矩 比 η= MrB/M，α = r1/r2，sin dφ/ 2≈ dφ /2，化简后求得：

由（4）式可得第一种破坏模式对应的极限荷载：

上述公式应用的前提条件是基础悬挑部分板厚不变，当考虑基础悬挑板厚变化的影响时，任意变截面处的环向内弯矩均小于支座处的弯矩 M。因此，在力矩平衡条件（1）式中，环向弯矩贡献的总力矩有所降低，令外悬挑端部厚度系数γ= h1/h ，考虑悬挑板厚折减效应［9］后，第一种破坏模式对应的极限荷载为：

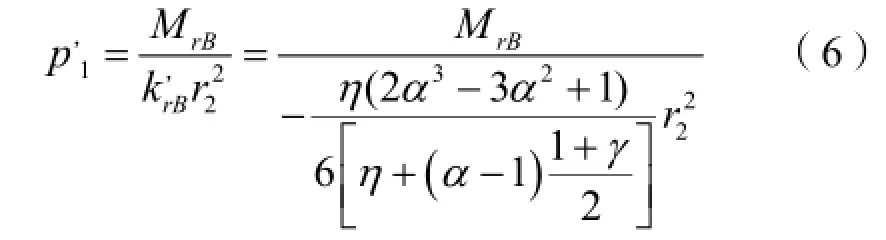
2）第六种破坏模式

图5 支座以内三角形小块隔离体

为求第六种破坏模式对应的极限荷载，取图（3f）支座以内的三角形小块为隔离体进行研究。该小块的中心角仍为 dφ，其上作用均载 p6，沿支座处环向单位弧长上，作用已求得的径向弯矩 MrB，沿两边单位长度上的环向极限弯矩 M，内外力对T-T轴（图5）的力矩平衡条件为：

式中： m0为三角形小块上的均载 p6对支座处单位弧长上的外力矩，从图5可知：

式（9）的适用条件为β ＜ η，则有 kr 6＜0， MrB＜0， M＜ 0。否则可能产生第五种破坏模式。

3.3 参量分析

为了比较第一种和第六种破坏模式下的极限荷载 p1与 p6大小，进行如下参量分析：

1） 悬挑外形系数α。根据风机圆形基础常用外形的统计数据，α ≥ 2.5；

2）悬挑部分径环向受弯承载力比η。根据弹性计算结果和塑性弯矩调幅效果［9］，η = 1.0～2.0；

计算结果见表1、表2和表3。

表1 极限荷载比P6/P1（β=0）

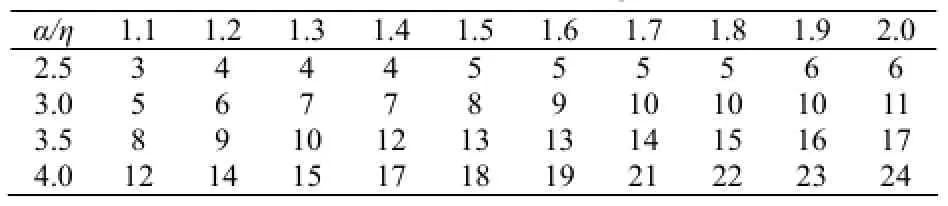
表2 极限荷载比P6/P1（β=0.5）

表3 极限荷载比P6/P1（β=1.0）

经过参量分析，可得出如下结论：

1）风机圆形基础的承载力由第一种破坏模式确定，第六种破坏模式不起控制作用。一方面，截面尺寸效应影响基础的破坏模式及相应的极限荷载。由式（5）或式（6）可知，P1与α2成反比，风机基础底板属于长悬臂构件，悬挑外形系数α较大，对P1值的折减远大于P6。从上述表格可知，P6多大于P1，根据机动定理，可选择极限荷载小的破坏模式作为承载力主控模式。另一方面，风机基础的内跨板直径小、厚度大，支座处钢质套环对圆板的转动存在有利约束作用，均从构造上进一步保证了不会产生第六种破坏模式。

2）烟囱规范的长悬挑圆形基础承载力计算公式不能用于风机基础设计。烟囱规范中受弯承载力计算公式根据基础悬挑长短分为两套，长悬挑时的弯矩公式是在同时产生第一和第六种破坏图形假定之上，基于经济性条件 M=M推导而来。联立风机基础极限荷载计算公式（5）式、（9）式，令β= M/Mo=1、p = p即可。烟囱规范的计算假t16定与风机基础实际破坏模式不符，套用该规范进行风机基础设计，影响基础的安全性。

3）基于第一种破坏模式，本文提出一种风机圆形基础的承载力计算公式。

当已知基底反力1p时，可计算基础的径环向截面受弯承载力rBM 和M，计算公式为：

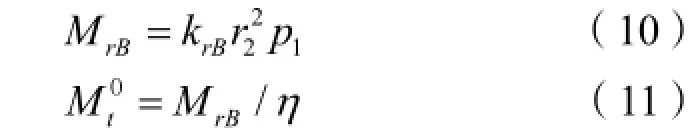
当已知基础配筋时，可计算基础底板的极限荷载 p1，计算公式同式（5）或（6）。

上述各式中， krB为弯矩比例系数，按式（4a）计算，η = 1.0～2.0。

4）与上述承载力公式相配套，提出优化基础底板配筋的设计建议。圆形基础常采用径环向配筋方式，悬挑部分径环向钢筋可由本文提出的承载力计算公式确定；基础内跨板的径向钢筋由悬挑部分延伸而来或在适当长度处截断，环向钢筋仅需按构造配置即可。由上述参量分析可知，当β= M/Mo= 0时，P6仍大于P1，说明基础内跨t板环向钢筋配置数量不会改变基础破坏模式。

4 结 论

1） 风机圆形基础的承载力由第一种破坏模式确定，第六种破坏模式不起控制作用。

2） 烟囱规范的长悬挑圆形基础承载力计算公式不适用于风机基础设计。该规范中长悬挑底板受弯承载力公式是在同时产生第一和第六种破坏图形假定之上，基于经济性条件推导而来，该假定与风机基础实际破坏模式不符。

3） 基于第一种破坏模式，本文提出一种风机圆形基础的承载力计算公式。

4） 与上述承载力公式相配套，提出优化基础底板配筋的设计建议。基础内跨板的径向钢筋由悬挑部分延伸而来或在适当长度处截断，环向钢筋仅需按构造配置即可。

参考文献：

［1］ EN1992-1 Eurocode 2： Design of concrete structures-part 1： General rules and rules for buildings ［S］.2001.

［2］ HENRIK SVENSSON.DESIGN OF FOUNDATIONS FOR WIND TURBINES［D］.Sweden：Lund University，2010.

［3］ 水电水利规划设计总院.风电机组地基基础设计规定（FD003-2007）（试行）［S］.北京：中国水利水电出版社，2007.

［4］ 朱艳艳，陈永安，姜琳， 等.WTF软件风电机组圆形扩展基础配筋计算［J］.西安：电网与清洁能源， 2010， 26（8）：64-68.

［5］ 中华人民共和国建设部. GB 50051━ 2002烟囱设计规范［S］.北京：中国计划出版社，2003.

［6］ 罗国强，鞠洪国.钢筋混凝土圆形板、环形板按极限平衡法的计算［J］.长沙：湖南大学学报， 1983， 10（1）： 71-80.

［7］ 蒋莉，许新勇，李静， 等.风机塔架基础接触非线性分析［J］.电网与清洁能源， 2011， 29（8）： 164-166.

［8］ 周洪博.西部地区风电场基础受力特性分析及结构优化研究［D］.包头： 内蒙古科技大学，2010.

［9］ 罗国强.钢筋混凝土圆形板、环形板计算与构造的若干问题［D］.

［10］ 沈聚敏，王传志，江见鲸．钢筋混凝土有限元与板壳极限分析［M］．北京：清华大学出版社，1993．

Calculation Method for Bearing Capacity of Circular Foundation Slab Supporting Onshore Wind Turbine

Mei Bixiang，Yang Min
（Faculty of Geotechnical Engineering， Tongji University， Shanghai 200092， China）

Abstract：Different from conventional building foundation， obvious load dynamic effect and large size of cross-section characterize the circular foundation of onshore wind turbine.Based on the failure patterns of circular slab foundation for conventional building， limiting equilibrium method is adopted to carry out theoretical derivation of limit load on wind turbine foundation in major failure patterns， and make impact analysis of the parameters including the section size and radial reinforcement of wind turbine foundation.The analysis results show that the bearing capacity of circular foundation slab is determined by the failure pattern of fan-shaped cantilever block and other failure patterns do not apply.Code of chimneys includes the calculation formula for the bearing capacity of long-cantilever circular foundation， which isn't suitable for the design of wind turbine foundation.Thus a new formula for calculating the bearing capacity of wind turbine circular foundation and relevant design suggestions are proposed， which may serve as a reference for the establishment of code of wind turbine foundation and the design of foundation engineering.

Key words：onshore wind turbine； circular foundation； failure pattern；-bearing capacity

中图分类号：TU312

文献标识码：A

文章编号：1004-9592（2016）02-0050-05

DOI：10.16403/j.cnki.ggjs20160213

收稿日期：2009-01-01

作者简介：梅毕祥（1979-），男，工程师，主要从事岩土工程方面的施工、设计和科研工作。