泥沙颗粒沿水深方向的受力研究

李世森，张 睿（天津大学，天津 300072）



泥沙颗粒沿水深方向的受力研究

李世森，张 睿
（天津大学，天津 300072）

摘要：对于研究泥沙群体性运动和实际工程的人来说，单颗粒泥沙的运动一直是研究问题的基础和关键。天然泥沙颗粒几乎都是非均匀的，其运动形式也具有随机性，这就造成颗粒附近流场的随机性。国内外学者对单颗粒泥沙受力情况的研究由来已久，文章采用Flow3D软件对单颗粒泥沙在定常流下的受力进行了数值模拟，得出了拖曳力系数和上举力系数关于泥沙颗粒直径、流速等因素的一定规律。

关键词：单颗粒泥沙；托曳力系数；上举力系数

引 言

河床表面的沉淀物颗粒受水流力的影响，水流力可以分为上举力和拖曳力。Shields（1936）研究床面泥沙颗粒力的平衡状态，进而推导出了无粘性均匀颗粒的起动拖曳力，并根据实验数据画出了起动拖曳力与雷诺数的关系图，及希尔兹曲线［1］。而后，Einstein和El-Samni（1949）［2］实验测量了颗粒由上下压力差产生的上举力。经过多年的研究，发现在一定范围内，拖曳力及上举力之间存在一定比例，结果受雷诺数等的影响，但仍未得出统一公式。

泥沙颗粒在水流中受拖曳力与上举力，拖曳力FD与上举力FL的一般表达式为：

式中：CD和 CL为拖曳力系数和上举力系数；u0为作用在床面泥沙颗粒上的流速。拖曳力系数与上举力系数由实验得出，具体不同流速下的实验已很多。

拖曳力系数是用来表示在流体中物体受牵引或受阻碍的程度的无量纲指数，其应用于拖曳力方程中，数值相对较小表示物体受拖曳力小，反之表示受拖曳力大。从物理模型实验到数值模拟，拖曳力系数已经得到了广泛大量的研究，上举力系数较少，一般认为两系数与颗粒形状、表面粗糙度、面积和水流条件等有关。然而，因为形状、水流等条件的变化对其影响过于复杂，仍不能有一个适用于任意雷诺数的统一的解析公式，当雷诺数较大甚至趋近于无穷时，各家结果差异较大，大量的实验数据分别形成了球形和非球形颗粒的拖曳力、上举力系数与雷诺数的近似曲线。Einstein和El-Sammi （1949）［2］测量了直接作用在塑料球上的压力差，以此作为上举力，并发现上举力系数CL对不同水流流速（测量点为球心所对上部0.15D处）保持一个定值。Davies和Samad（1978）［5］发现在边界处颗粒下层缝隙流动强烈时，当Re＜5颗粒所受上举力为负值，当R6＜5上举力为正值。Brayshaw（1983）［3］在Re*=52 000时，测得直径为16 mm的颗粒所受上举力与拖曳力之比为1.8。不同量级的Re*条件下，颗粒拖曳力和上举力比值和变化范围的研究还存在不足。McLauglin（1991）［6］、Mei（1992）［7］、Kurose和Konori（1999）［8］都测量了球形颗粒上举力系数，做出了CL与Re*的关系曲线，其范围主要在0＜Re*＜103，随Re*的增大CL逐渐变小，从他们的统计数据看，CL的变化范围在0～4之间，有可能出现负值。

上述国内外学者进行的各种数值、物理模型实验和理论研究，揭示了泥沙拖曳力和上举力的一定关系，对泥沙输移问题的研究做出巨大贡献。但拖曳力系数和上举力系数在大雷诺数条件下的可靠数据仍不够充足，影响因素研究有待深入。本文基于此背景，主要研究内容如下：利用Flow3D软件，在不同流速、不同高度、不同粒径条件下，进行单颗粒球形泥沙在紊流定常流中的模拟，得到流速和压力数据，进而得到泥沙颗粒受力和受扭的结果，并分析拖曳力系数和上举力系数，讨论大雷诺数下泥沙颗粒的受力情况和流场流态。

1 数学模型的建立与分析

1.1 基本思路

天然河床上的泥沙相互遮蔽，单颗粒受力泥沙较少，但单颗粒泥沙受力情况简单经典，天然泥沙形状各异，一般都为不规则颗粒，研究起来难度较大，故本文从球形单颗粒泥沙入手。不考虑底床坡度的情况下，本文模拟水平平面底上单颗粒球形泥沙固定（不移动、不旋转）在定常流中的受力情况。利用Flow3D软件建立三维模型，河床一头入口：x=0处设一简单牛顿流体，颗粒固定于流场稳定处，软件计算流场各点流速、压力，从而得出泥沙受力情况。模型采用嵌套式长方体（或立方体）网格，大网格模拟整个流场，小网格加密球体周围区域，精细刻画颗粒受力。三维立体水槽尺寸为24 m×1 m ×0.7 m，颗粒固定在13 m处（颗粒的位置经过建模计算检验，流体进入流场约10～11 m发展充分，流态稳定），流场进口边界条件为流量边界，出口为连续性边界，紊动模型采用RNG模型。模拟实验从流速、颗粒直径等因素的对比出发，进行建模和对照分析。

图1 网格示意（局部）

计算初始水深设定为0.6 m，大网格上表面边界设置为压力边界，取Fluid fraction为0，即液体上表面为空气的自由表面。沿水深方向的Z轴，网格设定为非均匀渐变网格，在［0，0.1］和［0.55，0.65］这两个区域内手动加密，保重沿Z向网格间距0.005 m，加密水流流速变化剧烈的水槽底部和浮动变化的液面区域。在保证有效计算的前提下，第一组模拟：颗粒直径为20 cm，进口流速为0.2 m/s，颗粒布置在水槽底至0.4 m内各个位置，各个位置间隔为0.05 m，模拟不同位置下在流场中的受力，目的为研究颗粒在流体上部的情况；第二组模拟：颗粒直径为10 cm，其实情况与第一组相同，目的在于与第一组模拟在粒径这一因素上对比；第三组模拟：颗粒直径为20 cm，颗粒始终布置在水槽底部，改变流速分别为0.1 m/s、0.2 m/s、0.3 m/s、0.4 m/s、0.5 m/s、0.6 m/s、0.7 m/s、1.0 m/s，目的为研究不同流速对颗粒受力的影响。模拟实验中，颗粒雷诺数范围为2×104～2×105，属于紊流，且颗粒雷诺数较大。

1.2 模型准确性和可行性研究

1.2.1 颗粒半径校正

必须注意，软件的网格划分为长方体（或立方体）网格，在描述球形颗粒时存在一定误差，不能完全精细描绘球体，故需要进行校准。Ladd（1994）［9］针对这一情况提出了“水力半径”这一概念进行修正，其方法是将一个已知半径ag的球体放置在蠕动流中计算其拖曳力，然后根据已知的Sangani和Acrivos（1982）［10］修正的拖曳力公式反推出水力半径a。本文采用Flow3D软件刻画球体时也遇到校准问题，且后处理工作用自己编制的Fortran程序计算，故综合考虑，采用球形颗粒沉降实验来校准颗粒计算半径，具体方法如下：用Flow3D软件模拟颗粒在竖直水槽中自由沉降的情况，模拟中以球体固定，水相对于球体运动来代替颗粒运动，模型进口和出口边界采用相同的速度边界，保证整个流场的速度保持相同值，模拟颗粒匀速运动的情况，计算四组：第一组水流方向为Z轴正向，重力加速度取9.8；第二组水流方向为Z轴正向，重力加速度取0；第三组水流方向为Z轴负向，重力加速度取9.8；第四组水流方向为Z轴负向，重力加速度取0。计算结果发现，项目1的（Pz+TAOX）与项目2的（Pz+TAOX）相减得到颗粒所受浮力等于2.835378E+01，项目3与项目4相减得到受浮力等于2.835286E+01，取两浮力值的平均值，反推得到直径为1.767908E-01 m。观察Flow3D模拟的结果文件，以迎水面流速为部分作为计算半径，结果为0.17 m。对于球与水的接触面的刻画，球体越大、网格越细越精确，故根据网格尺寸，结合模拟结果文件，可以得到各组实验的计算直径，以此直径进行后处理。

1.2.2 模型验证

拖曳力系数的研究不仅限于泥沙颗粒起动受力，在颗粒自由沉降中，阻力系数相当于拖曳力系数，统称为drag coefficient。为了验证模型和后处理工作的正确性，同时避免由于网格刻画不准确带来的数据差别，建立20 cm×20 cm×20 cm的立方体沉降模型，求解立方体受力，得出立方体颗粒阻力系数CD，与前人实验数据和经验值进行比较。

与前文球体颗粒沉降模型类似，用Flow3D软件模拟立方体颗粒在水槽中的自由沉降，固定立方体，水相对于立方体运动来代替颗粒运动，模型进口和出口边界采用相同的速度边界。模拟两组实验：第一组水槽竖向垂直，水流方向为Z轴正向；第二组水槽水平放置，水流方向沿X轴正向。模拟流场的雷诺数为Re=1×105，通过计算，求得：第一组FD=4.937 326 N，CD=0.987；第二组FD=4.585 866 N，CD=0.917。

国内外学者针对球形和非球形颗粒（如立方体等）的自由沉降（或自由降落）做了大量研究。阻力系数CD是流场和颗粒形状构成的复杂函数，Pettyjohn和Christiansen（1948）［11］以及Hartman和Coughlin（1993）［12］都将CD表示为CD=CD（Re，ψ），其中ψ为颗粒形状系数。

B.Krueger、S.Wirtz、V.Scherer（2015）［13］使用数码相机立体成像功能对颗粒自由沉降进行拍摄，从而得到不同形状颗粒的阻力系数， 4组立方体（cube）阻力系数分别为：1.033（Re≈2 000）、0.950（Re≈4 000）、1.018（Re≈4 000）、0.966 （Re∈8 000，10 000）。

庞启秀、徐金环、辛海霞（2006）［14］进行水槽实验研究了块体的水流拖曳力，以长方体为目标，研究了不同长高比下的拖曳力系数。实验水槽长20 m，宽0.3 m，高0.4 m，实验块体尺度长宽高各组变化。实验测量了以上19种块体尺度在平均流速0.3 m/s、0.6 m/s、0.8 m/s、1.2 m/s情况下的颗粒受力，可知雷诺数与数值实验在同一量级上，拖曳力系数CD和形状参数（bs/L2）1/3的关系如图2。从图中散点可知，形状参数（bs/L2）1/3在立方体时等于1，图中CD值在0.818和1附近。

综上，数值模拟数据与前人实验数据吻合，本文数值方法可行。

图2 庞启秀等水槽试验结果

2 数值模拟结果分析

2.1 水流流态

以0.2 m/s入口流速流体为例，此情况下，颗粒球心坐标为（13，0.5，0.1），直径为20 cm，颗粒雷诺数，属于紊流。从XZ面看，球形颗粒在来流冲击下，颗粒上部顶点附近存在一个流速较大的区域，颗粒近底部流速较小，水流到达球面后绕过球体运动，在水流方向上球后部有回流现象，且后部流速变化较前部剧烈。分别观察球形颗粒沿Z向上移0.05 m、0.10 m、0.15 m距离（颗粒仍固定不动）后XZ面颗粒局部流速等值线图会发现，与颗粒放置于床底对比发现，颗粒上移过程中，球下部顶点附近发展出一流速较大的区域，此区域流速与上部流速较大区域的流速接近，与周围流速值差别较大。随颗粒继续上升，此区域发展越来越大，当颗粒不受床面影响时，上下两个大流速区域沿颗粒对称轴对称，且水流方向上颗粒流速变化也对称，颗粒后部为流速较小的区域。对球心在（13，0.5，0.1）处颗粒，从XY面、YZ面分别观察Z=0 m、0.1 m、0.2 m和X=12.9 m、13.0 m、13.1 m位置的颗粒流速示意图，发现：高速区域集中在上半球前侧，低速区域在水流方向上球的前后均有分布，后部范围较大，且都集中在下半球，尤其球后部靠近床面处水流流速较低，变化剧烈，且流速图也充分显示了球形颗粒周围流速变化的对称性。

图3 流速等值线

2.2 上举力和拖曳力

泥沙颗粒在流场中受压力、由水的粘滞性带来的表面剪切力和重力作用，其中压力和剪切力均由水产生，可以综合为水流力，分解为上举力和拖曳力，也有不少学者并不分解，研究总的水流力。研究上举力和拖曳力的一般公式可得上举力系数CL和拖曳力系数CD，数码实验模拟大雷诺数情况下的颗粒受力，并针对不同因素进行分析。

对颗粒水中受力分析时，应同时考虑力和由力产生的扭矩作用。球体在水中受到压力，分可分解为三个方向的分量：Px、Py、Pz，受到剪切力，分解为三个方向：TAOx、TAOy、TAOz，压力全部指向球心，剪切力沿表面切线方向，会对颗粒产生绕坐标轴的扭矩：MTAOx、MTAOy、MTAOz，扭矩会使颗粒产生转动，通过模拟计算发现，扭矩很小，几乎可以忽略。在研究颗粒受力时，其合力作用点一直没有明确结论。本文分析，以TAOx为例，TAOx的作用点不在球心时，会产生对Y、Z轴的扭矩，故每一单元面积积分所求得的TAOx直接相加为TAOx的合力，然后求出合力距离Y、Z轴的距离，然后求解其扭矩的求法却不能直接累加，因为大小相同、方向相反的平行剪切力对合力大小不产生影响，但会产生一个扭矩。为了达到这一目的，编写了Fortran程序对模拟数据进行后处理。在达到计算精度的前提下，将球划分了180份，每一部分进行积分计算。

流速的选取对CL和CD的大小有不能忽略的影响。Einstein（1949）［2］采以距圆球顶面以下0.2D处作为理论床面，然后选取理论床面以上0.35D处的流速进行计算。本文考虑颗粒遮蔽度的影响，采用球前流速不受影响处的某一断面上、圆球迎水面直径所对的沿深度方向的垂线平均流速。通过建模计算发现，模型中流场10 m之后流态稳定，故计算中选取11 m处对应流速。

2.2.1 颗粒上升高度变化

天然河床上的泥沙颗粒以群体形式存在，泥沙层层叠叠，一般河床上有若干层泥沙，颗粒之间相互支撑相互遮蔽，自然就有相对上层的颗粒和相对下层的颗粒，为了研究泥沙距离底床高度这一因素对受力的影响，进行不同上升高度的球体受力模拟，本文从单颗粒上升入手，不考虑遮蔽问题，模拟目的在于测算泥沙由于上升所处水流状况的不同而造成的受力不同。本次模拟记为第一组，模拟中，首组泥沙颗粒固定在底床上，球体直径为20 cm，球心坐标为（13，0.5，0.1），接下来各组以0.05 m为间隔上升，上升过程中一直固定不动，嵌套网格也随之上升，控制入口流速为0.2 m/s，出口边界为出流边界。计算结果不在此详述。

由计算结果可知，直径为20 cm的球在入口流速为0.2 m/s流场中受力，压力Px、Py、PZ，其中 Py较小，几乎可以忽略；剪切力TAOx、TAOy、TAOz，与压力相比，剪切力都非常小，相差若干个量级，其中TAOx较TAOy、TAOz较大，但其对拖曳力系数CD的影响已经非常小，只能影响其小数点后第三位数字，TAOy、TAOz则影响太小完全可以忽略；剪切力对颗粒产生的扭矩MTAOx、MTAOy、MTAOz也非常小，几乎可以忽略。随着颗粒上升，垂线平均流速越来越大，在球体球心移动至0.30 m时（项目5），观察其垂线流速分布，流速全部相等，近似于自由落体沉降运动的情况，颗粒再上移至0.35 m、0.40 m情况也是如此。

拖曳力系数CD由Px和TAOx的合力求得，放置于床面时CD为0.524，颗粒上移CD迅速减小至0.2左右，且随颗粒上移CD越来越小，当颗粒接近自由落体情况时（即项目5、6、7）CD稳定在0.190～0.191附近。

上举力系数CL由Pz和TAOz的合力求得，床面时CL为3.685，颗粒上移CL逐渐减小，当颗粒接近自由落体情况时（即项目5、6、7）CD稳定在2.70附近。

图4 CD、CL与Z关系

2.2.2 颗粒直径变化

泥沙颗粒的形状会直接影响其所受上举力和拖曳力的大小，本文采用球体模拟泥沙颗粒，因此针对球体直径这一因素进行对照模拟。第二组模拟与第一组模拟相比，仅改变球体直径，其他不变，设定球体直径为10 cm，球心坐标为（13，0.5，0.05），以0.05 m为间隔上升，入口流速为0.2 m/s。计算结果略。

经计算发现，本组模拟中，Py、TAOy、TAOz、MAOX、MTAOY、MTAOZ依然与其他数据相差若干数量级，可以忽略。随着颗粒上升，垂线平均流速变化与第一组情况一致，在项目5时垂线流速几乎不变，进入沉降模式。放置于床面时，拖曳力系数CD为0.602，颗粒上移CD迅速减小至0.3左右，且随颗粒上移CD越来越小，当颗粒接近自由落体情况时（即项目5、6、7）CD稳定在0.303附近。

床面处上举力系数CL为5.401，颗粒上移CL逐渐减小，且随颗粒上移CD越来越小，当颗粒接近自由落体情况时（即项目5、6、7）CD稳定在在3.20～3.21附近。将第二组模拟得到的CD、CL与第一组对比如图5。

图5 第一组与第二组模拟CD、CL与Z关系对比

图6 第一组与第二组模拟曲线对比

对比发现，第二组模拟得到的CD、CL均大于第一组值，即半径越小CD、CL越大，且CD变化比CL大，但两组模拟曲线的变化趋势一致。

将第二组模拟的Px、Pz、TAOx、TAOz与第一组进行对比。

由四组对比曲线可知，Px、Pz、TAOx三个相对较大的值变化趋势相似，第一组模拟值远大于第二组，TAOz接近0，两组值最终都稳定在0附近。

2.2.3 流速变化

为了研究流场变化对颗粒受力产生的影响，改变入口速度，首先：第三组模拟，设定球体直径为20 cm，设定进口流速为0.4 m/s，然后如第一组模拟一样以0.0 5m为间隔将颗粒上移；第四组模拟，球体直径为20 cm，始终将颗粒固定于床面，改变入口流速，分别为：0.1 m/s、0.3 m/s、0.5 m/s、0.6 m/s、0.7 m/s、1.0 m/s，0.2 m/s与0.4 m/s分别在第一组和第三组模拟中计算过，其他条件均不变。

由计算结果可知，直径为20 cm的球在入口流速为0.4 m/s流场中受力，可以发现，与前两组相同，压力Py，剪切力TAOy、TAOz，扭矩MTAOX、MTAOY、MTAOZ相对很小，可以忽略。拖曳力系数CD和上举力系数CL沿垂线变化规律与前两组模拟一致，本模拟中球体球心移动至0.35 m时（项目6）时达到近似于自由落体沉降运动的情况。拖曳力系数CD床面时值为0.517，颗粒上移减小至0.211，随颗粒上移CD越来越小，项目4、5、6时CD稳定在0.188附近，项目7略大，为0.191。上举力系数CL由PZ和TAOZ的合力求得，此组床面时CL为1.279，小于第一组，且随颗粒上移CD越来越小，最终CD稳定在0.68附近，同样小于第一组。如图7。

图7 第一组与第三组模拟CD、CL与Z关系对比

从图7可以发现，拖曳力系数CD在流速改变时变化不大，两条曲线几乎吻合；上举力系数CL则变化较大，流速增大后CL变小，变小将近1/4，但曲线变化趋势相同。

第一组和第三组模拟得到的Px、Pz、TAOx、TAOz做对比，如图8。

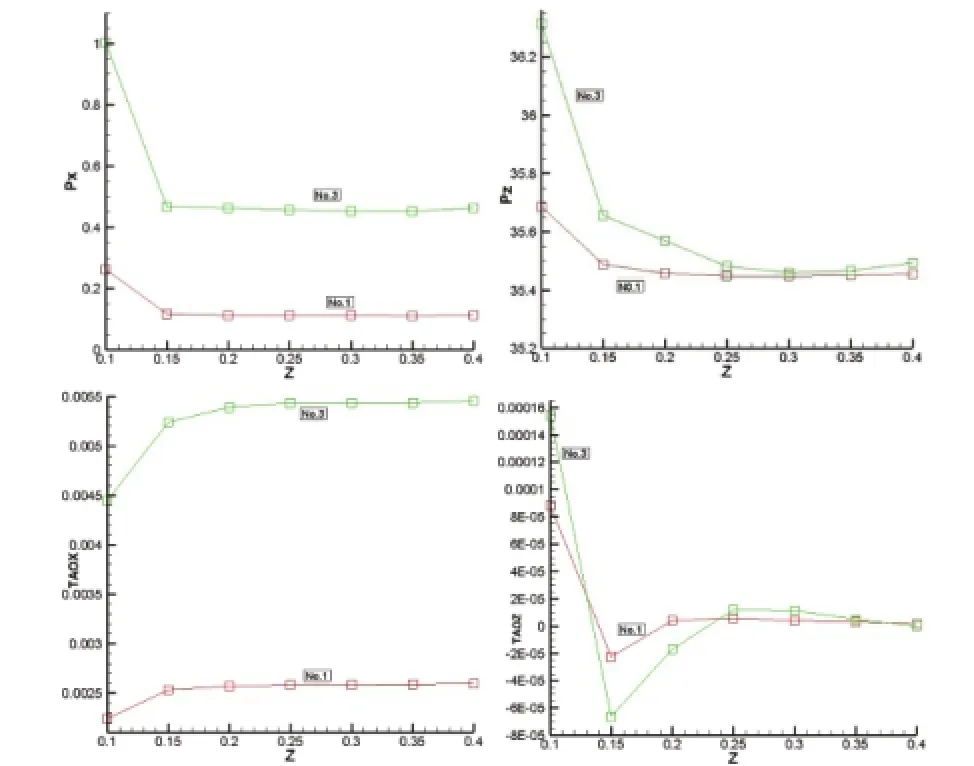
图8 第一组与第三组模拟曲线对比

由图8可知，流速较大的第三组模拟得到的Px、Pz、TAOx均大于第一组的值，其变化规律相似，其中Pz值两条曲线最终均稳定于35.5左右，相差较少，TAOz较小，两条曲线变化趋势类似，最终均稳定于0附近。

第四组模拟调整流速，通过观察结果可以发现，流速改变拖曳力系数CD几乎稳定不变，在0.52附近浮动，上举力系数CL随着流速增大越来越小，两值曲线如图9、图10。

图9 CD、CL与V关系做Px、Pz、TAOx、TAOz曲线

图10 Px、Pz、TAOx、TAOz关于流速V的曲线

由图9、图10可知，流速与Px、Pz、TAOx、TAOz的关系比较规律，其中流速与Px、Pz的曲线为平滑抛物线，与TAOx、TAOz的关系近似为一条斜线。

2.2.3 力臂、作用点分析

球体颗粒受到压力和剪切力，压力均指向球心，不会产生对球体的扭矩，剪切力沿表面切线方向，会产生对球体的扭矩。剪切力沿坐标轴分解：TAOx、TAOy、TAOz、TAOx，会产生绕Y轴和Z轴的扭矩，本文称其为MTAOXY、MTAOXZ，TAOx的力臂分别记为XZ、XY；与此相同，TAOy产生扭矩MTAOXY、MTAOXZ，力臂为YZ、YX；TAOz产生MTAOZX、MTAOZY，力臂为ZY、ZX；由此可得，剪切力关于三个坐标轴的总扭矩：MTAOX、MTAOY、MTAOZ。以第一组模拟项目一为例，见表1。

表1 受力计算

由表1可知，球体受到的扭矩MTAOX、MTAOY、MTAOZ近似为零，剪切力分别产生的扭矩MTAOXY、MTAOXZ、MTAOYX、MTAOYZ、MTAOZX、MTAOZY也近似为零，相比之下MTAOXY、MTAOZY虽然也很小，但比其他量大若干数量级；观察剪切力TAOx、TAOy、TAOz，相比TAOx较大，TAOz次之，TAOy近似为零；本项目球体半径为0.10 m，观察剪切力对应的力臂，MTAOXY、MTAOZY对应力臂XZ、ZX分别为0.013 m、-0.014 m，靠近球心，XY、ZY则近似为零，位于球心上。综上可发现，剪切力与压力相比较小，相比之下仅TAOx、TAOz需考虑，其产生的扭矩MTAOXY、MTAOZY较大，故总扭矩仅MTAOY需考虑，但仍然非常小，而且剪切力作用线几乎都集中于球心附近，将三个分力合成，剪切力合力大小为0.002 kN，作用点为（-0.014，0，0.013）。其他组模拟中发现，扭矩MTAOX、MTAOY、MTAOZ也很小，可以忽略，剪切力作用点也在球心附近。

3 结 论

本文以球体代替泥沙，对河床上的单颗粒泥沙在定常流中的受力进行了研究，通过数值模拟方法，分析其受力、受扭情况，并结合多个变量研究了泥沙颗粒拖曳力系数和上举力系数的变化规律。

研究表明：1）泥沙颗粒在水流中受到水压力和剪切力的影响，剪切力对颗粒产生扭矩，但扭矩较小；2）在Rep∈（1×104，2×105）时，流速改变对拖曳力系数CD影响非常小，颗粒半径则影响较大，球体半径越小拖曳力系数CD越大，随着颗粒离开床面上移，CD迅速减小，当颗粒处于流速沿垂线变化不大的高度时，CD稳定在一定范围内；在此范围内，上举力系数CL大于拖曳力系数CD，CL变化范围比CD大，流速越大CL越小，颗粒直径越大CL也越小，与拖曳力系数相同的是，随着颗粒沿垂线上移，CL不断减小，当球前流速沿垂线方向几乎不变时，最终稳定在一定范围内。

参考文献：

［1］ Shields A.Anwendung der Aechlichkeitsmechanik und der Turbulenzforschung auf die Geschiebewegung ［J］.Berlin， Mit.Preussische Versuchsanstalt fur Wasserbau，1936.

［2］ Einstein H A， E A EO-Samni.Hydrodynamic Forces on A Rough Wall［J］.Rev Modern Phys， 1949， 21（3）：520-524.

［3］ Brayshaw A C， L E Frostick， L Reid.The hydrodynamics of particle clusters and sediment entrainment in course alluvial channels ［J］.Sedimentology，1983， 30：137-143.

［4］ Schmeeckle M W， Nelson J M， Shreve R L.Forces on stationary particles in near-bed turbulent flows ［J］.Geophys Res， 2007：112.

［5］ Davies T R H， M F A Samad.Fluid dynamic lift on a bed particle ［J］.Hydraul Div Am Soc Civ Eng， 1978，104：1171-1182.

［6］ McLaughlin J B.Internal migration of a small sphere in linear shear flows ［J］.Fluid Mech， 1991：261-274.

［7］ Mei R.An approximate expression for the shear lift force on a particle at a finite Reynolds number ［J］.Multiphase Flow， 1992， 18：145-147.

［8］ Kurse R， Komori S.Drag and lift forces on a rotating sphere in a linear shear flow ［J］.Fluid Mech，1999，384：183-206.

［9］ Ladd A J C.Numerical simulations of particle suspensions via a discretized Boltzmannequation.Part I.Theoretical foundation ［J］.Fluid Mech， 1994，271：285-309.

［10］ Sangani A S， Acrivos A.Slow flow through a periodic array of spheres ［J］.Multiphase Flow， 1982， 8：343-360.

［11］ Pettyjohn E S， Christiansen E B.Effect of Particle Shape on Free-Settling Rates of Isometric Particles ［J］.Chem Eng Prog， 1948， 44（2）：157.

［12］ Hartman M， Coughlin R W.On the Incipient Fluidized State of Solid Particles ［J］.Collect Czech Chem Commun，1993， 58：1213.

［13］ Krueger B， Wirtz S， Scherer V.Measurement of drag coefficients of non-spherical particles with a camera-based method ［J］.Powder Technology， 2015，278：157-170.

［14］ 庞启秀，徐金环，辛海霞.块体形状对水流拖曳力的影响［J］.水道港口，2006，27（1）：5-9.

Analysis of Forces on Sediment Particles at Different Depth

Li Shisen1，Zhang Rui2
（Tianjin University， Tianjin 300072， China）

Abstract：It is the foundation and key point for one who studies the swarming movement of sediment particles and participates in the practical engineering to fully understand the movement of single sediment particle.The most natural sediment particles are non-uniform and they move at random， which results in randomness of the flow field near sediment particles.In a very long time， the stress of single sediment particle has been studied in China and abroad.Now， a numerical simulation is made for the stress of single sediment particle under the steady flow by using Flow3D software， which produces the variation rules of towing and uplifting coefficients under different diameters of sediment particle and velocities of flow.

Key words：single sediment particle； towing force coefficient； uplift force coefficient

中图分类号：U652.2+1

文献标识码：A

文章编号：1004-9592（2016）02-0006-07

DOI：10.16403/j.cnki.ggjs20160202

收稿日期：2015-10-14

作者简介：李世森（1969-），男，副教授，主要从事泥沙运动规律及淤积研究。