基于振动模型的采煤机摇臂齿轮局部故障频谱分析
2016-07-19段蛟龙许春雨宋建成田慕琴郭俊严正凯关强
段蛟龙, 许春雨, 宋建成, 田慕琴, 郭俊, 严正凯, 关强
(1.太原理工大学 煤矿设备与智能控制山西省重点实验室, 山西 太原 030024;2.山西菲利普斯煤矿机械修造有限公司, 山西 晋城 048200)
基于振动模型的采煤机摇臂齿轮局部故障频谱分析
段蛟龙1,许春雨1,宋建成1,田慕琴1,郭俊1,严正凯2,关强2
(1.太原理工大学 煤矿设备与智能控制山西省重点实验室, 山西 太原030024;2.山西菲利普斯煤矿机械修造有限公司, 山西 晋城048200)
摘要:从齿轮传动机理出发,考虑直齿轮局部故障对啮合振动的调幅调频作用,建立了直齿轮局部故障振动信号模型;在直齿轮局部故障模型的基础上,分析了行星齿轮结构特征及振动信号产生和变化规律,建立了行星齿轮局部故障振动信号模型。对带有不同齿轮局部故障的摇臂进行加载试验,对采集的试验振动信号进行了频谱分析,分析结果表明,所建立的齿轮故障振动信号模型能客观、准确地反映摇臂齿轮故障状态,应用频谱分析方法可实现摇臂齿轮局部故障诊断。
关键词:采煤机摇臂; 直齿轮; 行星齿轮; 局部故障; 振动信号; 频谱分析
网络出版地址:http://www.cnki.net/kcms/detail/32.1627.TP.20160705.1459.009.html
0引言
由于井下工作面环境恶劣和煤壁结构复杂,易引起采煤机摇臂齿轮点蚀、剥落和断裂等局部故障,摇臂齿轮故障占采煤机故障的34.2%[1]。摇臂齿轮故障将导致采煤机无法正常工作,从而造成工作面停工,严重影响煤矿的正常生产。因此,研究摇臂齿轮局部故障的早期诊断具有重要意义。
国内学者利用智能故障诊断方法对采煤机摇臂齿轮故障进行诊断。陈曦晖等[2]利用多尺度均方根提取振动信号中的能量,通过BP神经网络实现了直齿轮故障识别;胡晓等[3]采用多尺度熵提取振动中的能量,能有效抑制高频噪声信号的影响,故障识别率得到进一步提高;陈渊等[4]将PSO-SVM方法应用于采煤机齿轮故障诊断,实现了小训练样本下的齿轮故障识别。由于采煤机摇臂为多级齿轮传动结构,振动信号中含有的信息较为复杂,使得智能故障诊断方法识别率低。目前,这些方法还没有应用于现场。因此,建立摇臂齿轮故障振动信号模型,并分析其频谱特征非常必要。
还有学者通过信号建模方法对故障齿轮箱进行了研究,MCFADDEN P D等[5]建立了行星齿轮不同故障齿轮的故障模型,揭示了振动信号频谱的非对称性,但没有考虑啮合位置变化对振动信号的调幅作用,不能准确反映实际情况;FENG Zhipeng等[6]深入分析了啮合位置变化对振动信号的调幅作用,建立了行星齿轮故障模型,但没有对多点啮合情况下的故障调幅调频作用加以分析。
针对以上故障模型存在的不足,本文从齿轮传动机理出发,建立了直齿轮局部故障振动信号模型;在此基础上,考虑行星齿轮啮合位置变化对振动信号的调幅和多点啮合振动作用,建立了行星齿轮局部故障振动信号模型;最后,通过摇臂加载试验对比分析试验振动信号和故障模型的频谱特征,验证所建立故障振动信号模型的准确性;应用频谱分析方法,实现了摇臂齿轮故障诊断。
1摇臂齿轮箱结构分析
以山西晋城无烟煤矿业集团有限责任公司寺河矿主力生产采煤机EICKHOFF SL500为研究对象,其结构如图1所示。摇臂齿轮箱由两级直齿轮和两级行星齿轮组成,两级直齿轮用于满足采煤机大采高的要求,同时也起到一定的减速作用,行星齿轮主要起传动减速的作用。
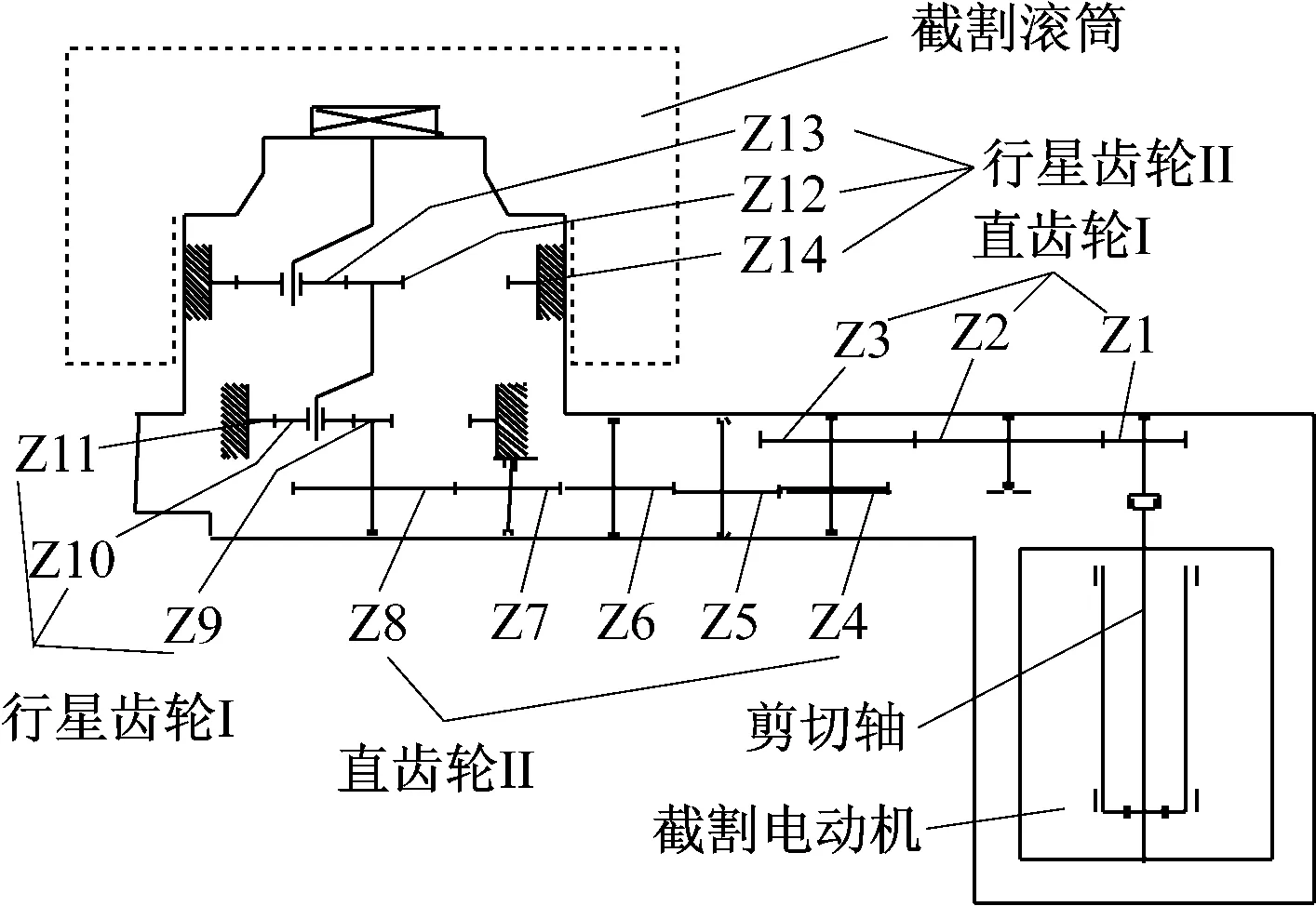
图1 EICKHOFF SL500采煤机摇臂齿轮传动结构
摇臂齿轮箱的直齿轮啮合副的啮合位置固定不变,为准确测量振动信号,传感器安装在该齿轮的轴承座上,啮合处产生的振动信号到传感器的距离是固定不变的。因此,传感器所接收到的振动信号强度不会随着直齿轮的转动而发生变化。行星齿轮相对于直齿轮更加复杂,其结构如图2所示。传动过程中,内齿圈固定不动,行星轮围绕太阳轮转动,这样的传动结构会使太阳轮-行星轮和行星轮-内齿圈啮合副的啮合位置随行星架旋转而变化,传感器安装在内齿圈外壁上。因此,传动过程中太阳轮-行星轮啮合副和内齿圈-行星轮啮合副的啮合位置到传感器的距离将发生周期性变化,啮合位置远离传感器时,传感器接收到的振动信号减弱,靠近时,传感器接收到的振动信号增强。啮合位置的变化将对局部故障引起的冲击振动产生额外的调幅作用。因此,需要分别建立采煤机摇臂直齿轮和行星齿轮的故障振动信号模型。
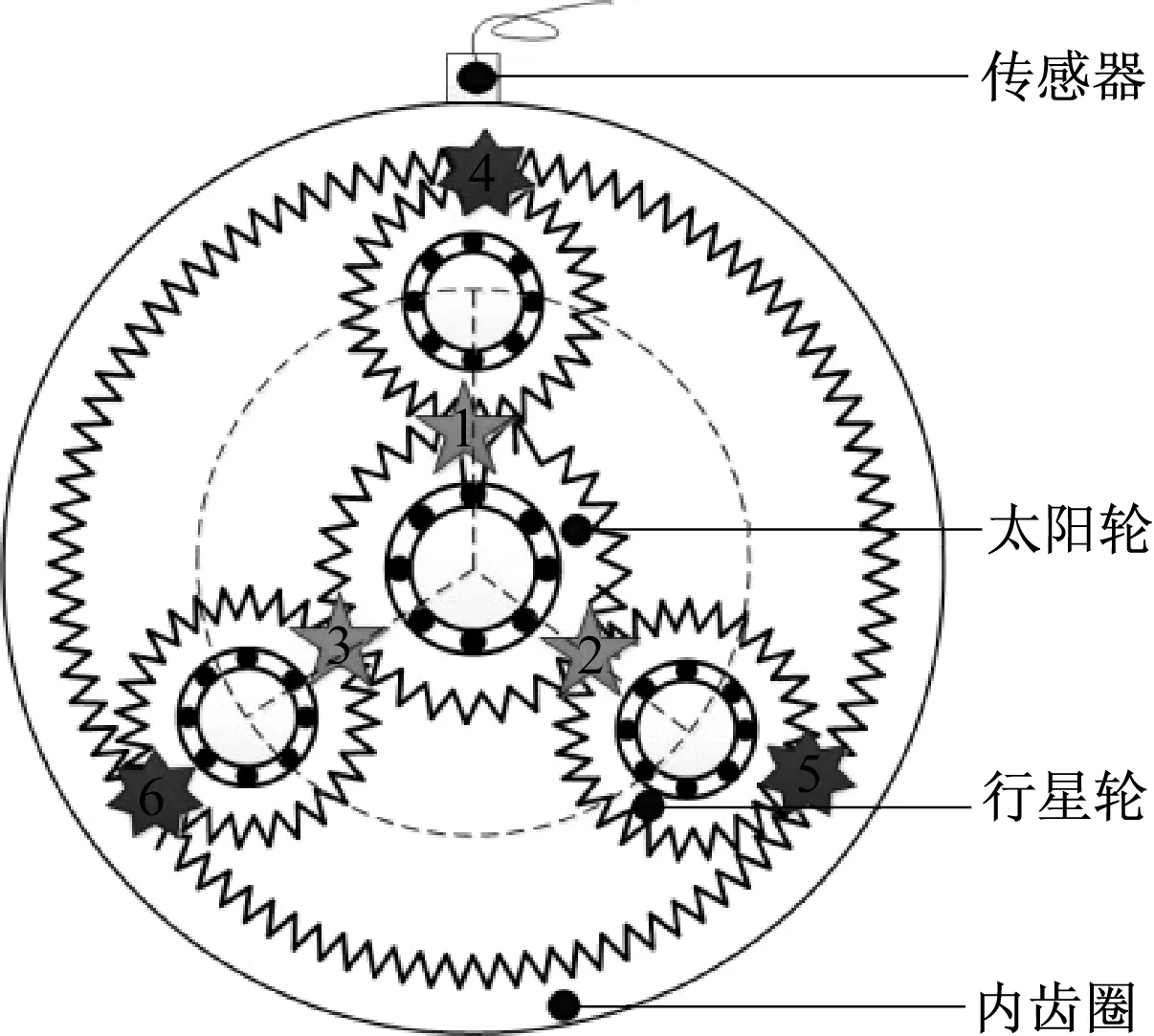
图2 摇臂行星齿轮结构
2摇臂齿轮故障振动信号模型
2.1摇臂直齿轮故障振动信号模型
在采煤机摇臂齿轮箱使用过程中,当带有局部故障的轮齿参与啮合时,由于故障轮齿的齿面不平整而受力不均,会造成接触面油膜破裂,产生冲击振动现象。冲击振动信号就是齿轮局部故障特征信号[7]。
正常采煤机摇臂直齿轮传动过程中齿轮啮合产生啮合振动,啮合振动信号的频率与齿轮转动速度和齿轮齿数有关。当直齿轮的轮齿发生局部故障时,齿轮转动一周发生一次故障啮合,产生的冲击振动信号频率为该齿轮的转动频率[8]。故障产生的冲击振动将对直齿轮固有啮合振动产生调幅调频作用[9-10],载波频率为直齿轮啮合频率,调制频率为局部故障直齿轮转动频率。因此,本文所建立的直齿轮故障振动信号模型如式(1)所示。
(1)
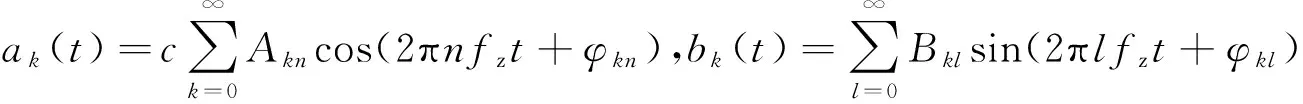
为简化故障模型,在此只考虑基频信号的作用,式(1)可简化为
x(t)=[1+Acos(2πfzt+φ)]×
cos[2πfmzt+Bsin(2πfzt+φ)+θ]
(2)
式中:A和B分别为调幅和调频函数的幅值;φ和θ均为初始相位。
根据三角函数的性质,式(2)可展开为
x(t)=cos[2πfmzt+Bsin(2πfzt)]+
(3)
为表达简便,令
(4)
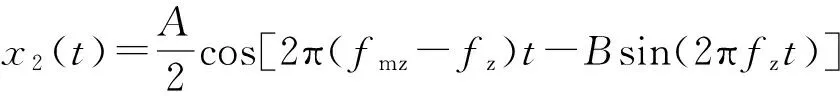
将x1(t)用欧拉公式展开可得
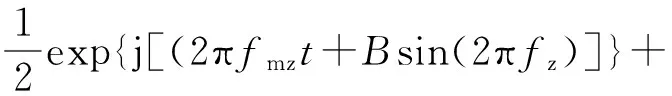
(5)

(6)
对式(6)进行傅里叶变换可得
(7)
根据以上推导过程,X(f)推导结果如式(8)所示。
X(f)=X1(f)+X2(f)+X3(f)=
(8)
由式(8)可见,摇臂直齿轮发生局部故障时,直齿轮振动信号频谱图中将出现fmz±mfz的直齿轮局部故障边频带。
2.2摇臂行星齿轮故障振动信号模型
2.2.1摇臂内齿圈故障振动信号模型
当摇臂行星齿轮的内齿圈发生局部故障时,在行星架一个转动周期内,每个行星轮都将和内齿圈故障部位发生一次啮合,故障产生的冲击振动将对内齿圈-行星轮啮合振动产生调幅调频效应,故障调幅调频信号的频率和行星轮的个数有关;太阳轮-行星轮这组啮合振动由于啮合位置的变化将发生调幅现象。因此,本文所建立的摇臂内齿圈故障振动信号模型如式(9)所示。
x(t)=[1-cos(2πfct+α)]cos(2πfxt+θ1)+[1+Acos(2πfrt+φ)]cos[2πfx+Bsin(2πfrt+φ)+θ2]
(9)
式中:fx为行星齿轮啮合频率;fc为行星架转动频率;fr为内齿圈故障频率,它和行星轮的个数有关,fr=nfc(n为行星轮个数)。
同理,由式(9)推导可得
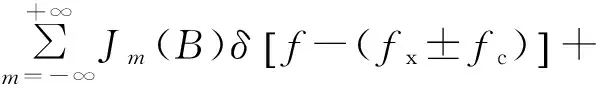
(10)
由式(10)可见,摇臂内齿圈发生局部故障时,行星齿轮振动信号频谱图中将出现fx±fc的行星架旋转调幅边频信号以及fx±mfr的内齿圈故障边频带。
2.2.2摇臂行星轮故障振动信号模型
当行星轮发生局部故障时,故障行星轮转动一周,既要和内齿圈发生故障啮合,又要和太阳轮发生故障啮合,故障冲击振动将对内齿圈-行星轮和太阳轮-行星轮啮合2组振动产生调幅调频作用。因此,本文所建立的摇臂行星轮局部故障振动信号模型如式(11)所示。x(t)=[1-cos(2πfct+α)][1+Acos(2πfpt+φ)]×
cos[2πfx+Bsin(2πfpt+φ)+θ]
(11)
式中:fp为行星轮故障频率,其值为行星轮转动频率和行星架转动频率的差值,fp=fpr-fc,fpr为行星轮转动频率。
同理,由式(11)推导可得
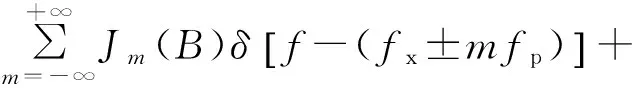
(12)
由式(12)可见,摇臂行星轮发生局部故障时,行星齿轮振动信号频谱图中将出现fx±mfp和fx±fc±mfp行星齿轮故障边频带。
2.2.3摇臂太阳轮故障振动信号模型
当太阳轮发生局部故障时,太阳轮相对于行星架轮转动一周内将和每个行星轮发生一次故障啮合,故障冲击振动将对太阳轮-行星轮啮合振动产生调幅调频作用,故障调幅调频信号的频率和行星轮的个数有关;内齿圈-行星轮这组啮合振动由于啮合位置变化,将发生调幅现象。因此,本文所建立的太阳轮局部故障振动信号模型如式(13)所示。
x(t)=[1-cos(2πfct+α)]cos(2πfxt+θ2)+
[1-cos(2πfsrt+α)][1+Acos(2πfst+φ)]×
cos[2πfx+Bsin(2πfst+φ)+θ1]
(13)
式中:fsr为太阳轮转动频率;fs为太阳轮故障频率,fs=nfsr-fc。
同理,由式(13)推导可得
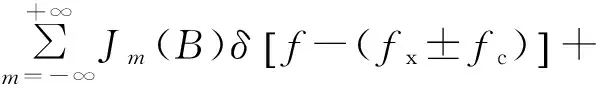
(14)
由式(14)可见,摇臂太阳轮发生局部故障振动时,行星齿轮振动信号频谱图中将出现fx±fc的行星架旋转调幅边频信号以及fx±fsr±mfs太阳轮故障边频信号带。
3试验及检测信号分析
3.1现场试验
采煤机摇臂加载试验在某公司采煤机维修车间进行。试验系统由水轮测功器、摇臂和振动信号测试系统等组成。为了测量振动信号,在摇臂直齿轮轴承座和行星齿轮内齿圈各个方向上布置了多个加速度传感器,选取垂直方向的振动信号进行分析。分别对正常和带有直齿轮、内齿圈、行星轮和太阳轮局部故障的摇臂进行加载测试。试验中,信号的采样率为10 kS/s,电动机实测转速为1 492 r/min,测量的振动信号时域波形如图3所示。
(a) 正常直齿轮
(b) 故障直齿轮
(c) 正常行星轮
(d) 故障内齿圈

(e) 故障行星轮

(f) 故障太阳轮
根据摇臂齿轮参数和电动机转速计算摇臂直齿轮和行星齿轮啮合频率,以及各个齿轮局部故障特征频率,结果见表1[13]。

表1 摇臂齿轮特征频率 Hz
3.2振动信号分析
在Matlab平台中对摇臂加载试验所测量的振动信号进行频谱分析,分析结果如下:
(1) 正常状态。采煤机摇臂正常状态下直齿轮和行星齿轮振动信号频谱如图4所示。由图4(a)可见,在直齿轮啮合频率周围出现了微弱的边频信号,这是由于直齿轮制造误差所引起的。由图4(b)可见,在行星齿轮啮合频率周围出现了频率为fx±nfz的边频信号,边频间隔为行星架的转动频率,这是由于行星轮围绕太阳轮转动引起啮合位置周期性变化,对啮合振动起到了调幅作用。
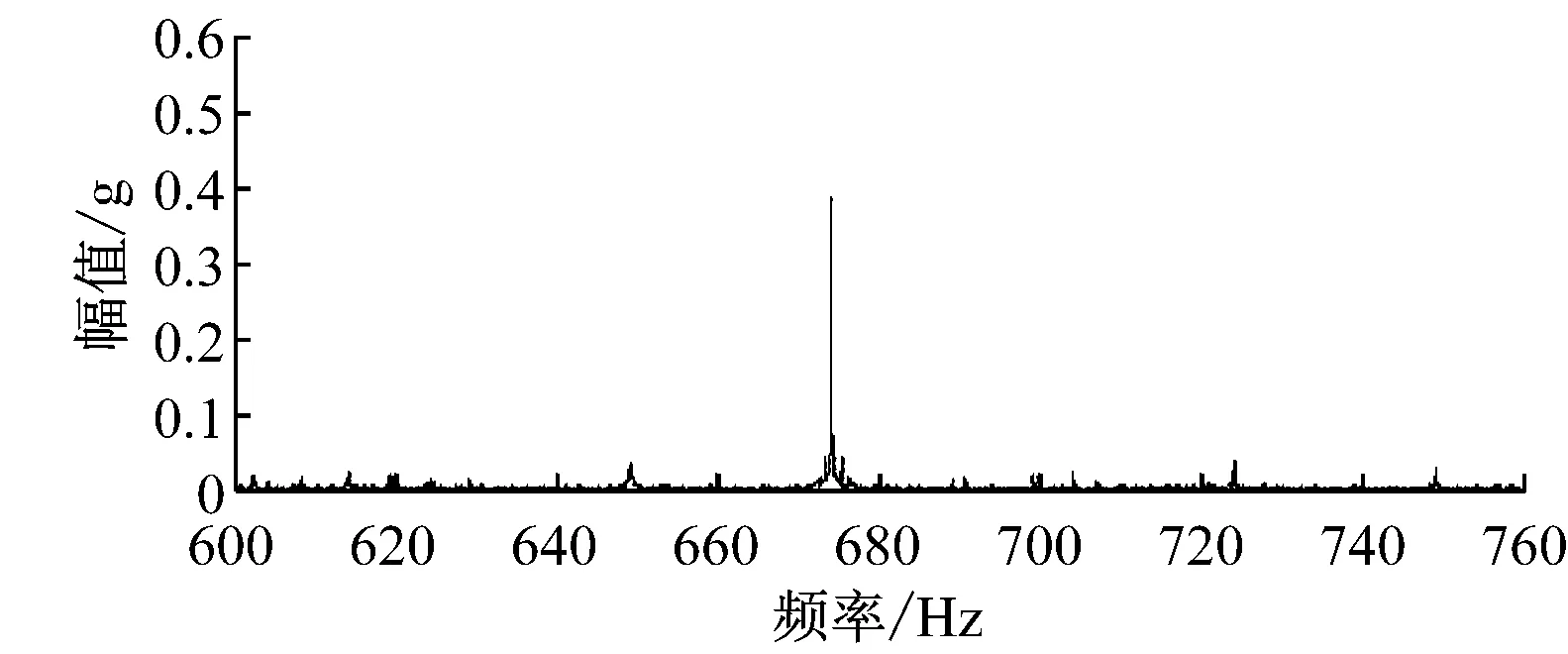
(a) 正常直齿轮频谱
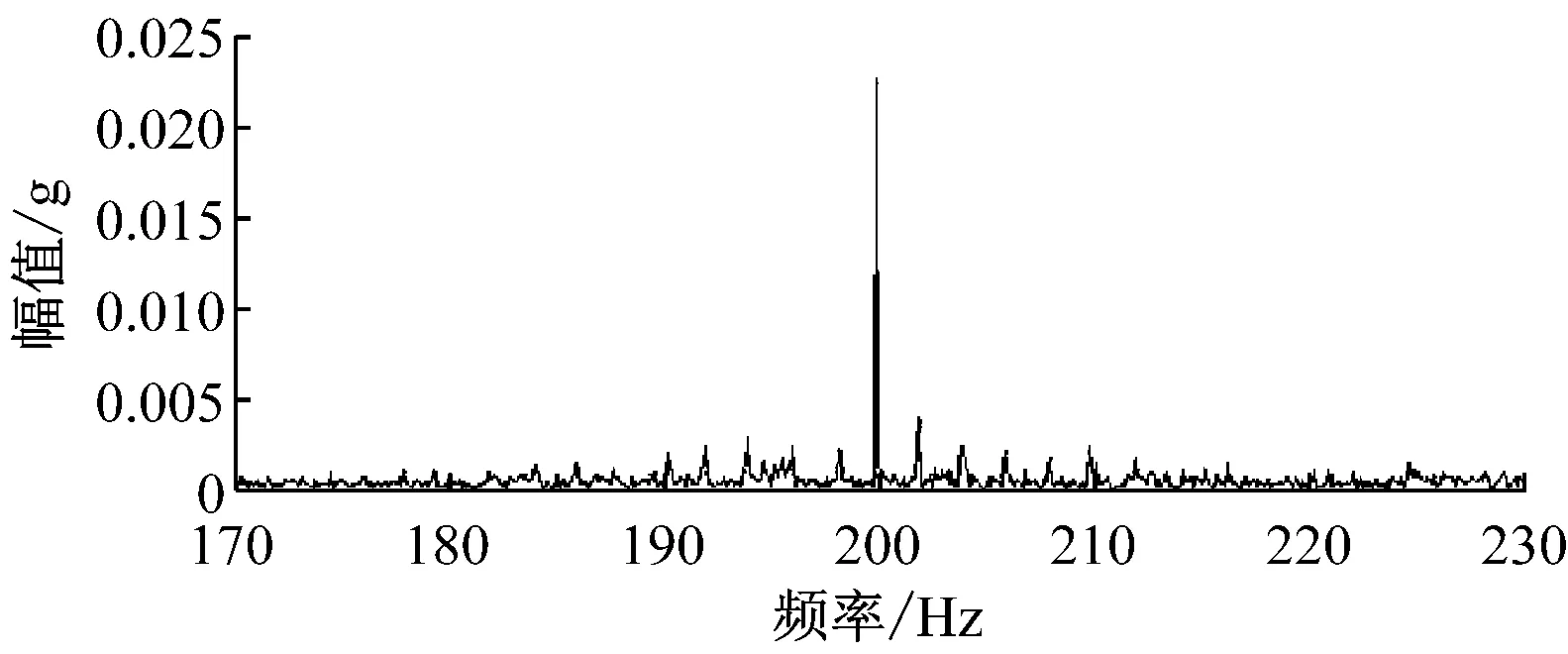
(b) 正常行星齿轮频谱
(2) 直齿轮故障。采煤机摇臂直齿轮故障状态下的振动信号频谱如图5所示。由图5可见,在直齿轮啮合频率周围出现了fmz±fz和fmz±2fz故障边频信号,边频宽度和理论计算的直齿轮Z1转动频率一致。这些现象说明直齿轮故障信号对固有啮合信号起到了调幅调频作用,与理论分析一致。
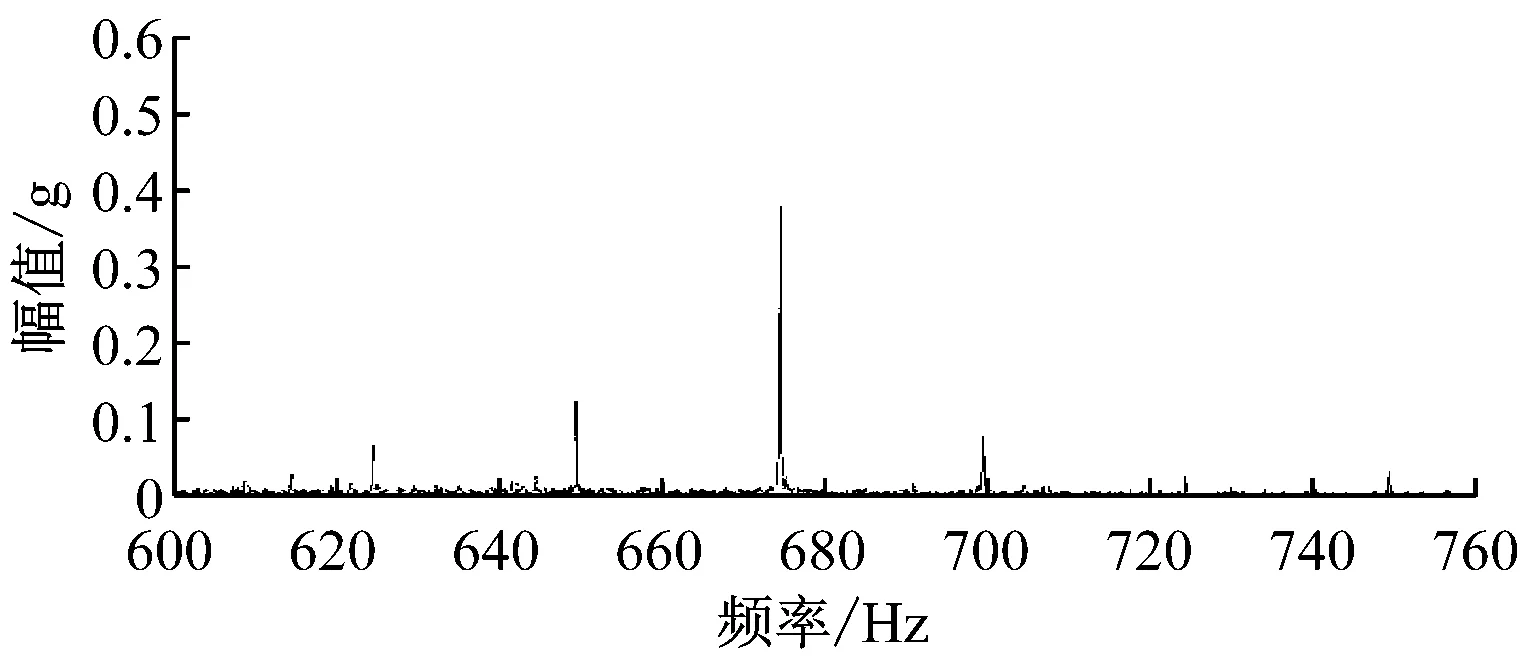
图5 直齿轮振动信号频谱
(3) 内齿圈故障。采煤机摇臂内齿圈故障状态下的振动信号频谱如图6所示。由图6可见,行星齿轮啮合频率周围出现了fx±fc边频信号,这是由于啮合位置变化对行星轮-太阳轮这组啮合振动信号起到了调幅作用,同时,在啮合频率周围出现了fx±fr,fx±2fr和fx+5fr内齿圈故障边频信号。

图6 内齿圈故障振动信号频谱
上述频谱特征说明内齿圈存在局部故障。
(4) 行星轮故障。采煤机摇臂行星轮故障状态下的振动信号频谱如图7所示。由图7可见,行星齿轮啮合频率周围出现了fx+fc+fp,fx-fc-fp,fx-2fp等边频信号,这是由于啮合位置变化引起的调幅和故障行星轮调幅调频作用的结果。远离啮合频率的边频信号由于幅值较小,淹没在噪声信号中。
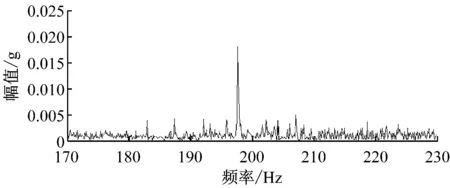
图7 行星轮故障振动信号频谱
(5) 太阳轮故障。采煤机摇臂太阳轮故障状态下振动信号频谱如图8所示。由于实际应用中3个行星轮不可能完全意义上相同,所以故障频率为理论计算值的1/3;由于太阳轮-行星轮啮合位置距离传感器较远,所以故障边频信号幅值较小,但仍然能识别出fx±nfs/3的故障边频带。fx±fc边频信号是由于内齿圈-行星轮啮合位置变化所引起的。

图8 太阳轮故障振动信号频谱
4结语
以采煤机摇臂齿轮为研究对象,分析了摇臂齿轮箱的传动特点,对摇臂直齿轮和行星齿轮振动信号产生及变化规律进行了深入研究:
(1) 分别建立了采煤机摇臂直齿轮和行星齿轮局部故障振动信号模型,该故障振动信号模型能更加客观、准确地反映摇臂齿轮局部故障状态。
(2) 推导了采煤机摇臂齿轮局部故障振动信号模型解析式,得到了各齿轮故障振动信号频谱,并应用频谱分析方法实现了采煤机摇臂齿轮的故障诊断。
(3) 分析了采煤机摇臂各齿轮故障振动信号频谱特征,发现了不同齿轮故障振动信号频谱变化规律,实现了采煤机摇臂齿轮故障定位。
参考文献:
[1]周久华,米林.采煤机摇臂齿轮箱故障与可靠性分析[J].内蒙古科技与经济,2011,9(3):39-41.
[2]陈曦晖,吴行标,程刚,等.基于多尺度均方根-BP神经网络的采煤机摇臂齿轮故障诊断[J].制造业自动化,2013,35(13):49-51.
[3]胡晓,钱沛云,陈曦晖,等.基于多尺度熵-BP神经网络的采煤机摇臂齿轮故障诊断[J].制造业自动化,2014,36(18):4-7.
[4]陈渊,马宏伟.基于PSO-SVM的采煤机摇臂齿轮箱故障诊断研究[J].煤矿机械,2015,36(10):303-306.
[5]MCFADDEN P D,SMITH J D. An explanation for the asymmetry of the modulation sidebands about the tooth meshing frequency in epicyclic gear vibration[J]. Proceedings of the Institution of Mechanical Engineers,Part C:Journal of Mechanical Engineering Science,1985,199(1):65-70.
[6]FENG Zhipeng, ZUO Mingjian. Vibration signal models for fault diagnosis of planetary gearboxes[J]. Journal of Sound and Vibration,2012,331(22):4919-4939.
[7]张进,冯志鹏,褚福磊.基于时间-小波能量谱的齿轮故障诊断[J].振动与冲击,2011,30(1):157-161.
[8]郜立焕,周长生,杨玮,等.齿轮故障诊断与分析[J].煤矿机械,2006,27(8):185-187.
[9]李宝年. 齿轮箱故障诊断研究[J].煤矿机械,1997,18(1):41-43.
[10]丁康,孔正国.振动调幅调频信号的调制边频带分析及其解调方法[J].振动与冲击,2005, 24(6):9-12.
[11]冯志鹏,赵镭镭,褚福磊.行星齿轮箱齿轮局部故障振动频谱特征[J].中国电机工程学报,2013,33(5):119-127.
Spectrum analysis of partial failure of shearer rocker gear based on vibration model
DUAN Jiaolong1,XU Chunyu1,SONG Jiancheng1,TIAN Muqin1,GUO Jun1,YAN Zhengkai2,GUAN Qiang2
(1.Shanxi Key Laboratory of Mining Electrical Equipment and Intelligent Control,Taiyuan University of Technology, Taiyuan 030024, China;2.Shanxi Phillips Coal Mine Machinery Manufacturing Co., Ltd., Jincheng 048200, China)
Abstract:A partial failure vibration signal model of spur gear was established starting from gear drive mechanism and considering both amplitude modulation and frequency modulation effects of meshing vibration due to partial spur gear damage. Based on partial failure model of spur gear, structure feature of planetary gear and vibration signal generation and changing rule were analyzed, and partial failure vibration signal model of planetary gear was established. Load test of rocker arm with different gear partial failures and spectrum analysis of collected vibration signal were conducted, the results show that the model of gear fault vibration signal model can objectively and accurately reflect failure state of rocker gear, and using the method of spectrum analysis can achieve partial failure diagnosis of rocker gear.
Key words:shearer rocker arm; spur gear; planetary gear; partial failure; vibration signal; spectrum analysis
文章编号:1671-251X(2016)07-0034-06
DOI:10.13272/j.issn.1671-251x.2016.07.009
收稿日期:2016-01-22;修回日期:2016-05-17;责任编辑:胡娴。
基金项目:山西省科技重大专项项目(20131101029)。
作者简介:段蛟龙(1988-),男,四川内江人,硕士研究生,研究方向为煤矿设备状态监测与故障诊断,E-mail:duanjiaolong@163.com。
中图分类号:TD632
文献标志码:A网络出版时间:2016-07-05 14:59
段蛟龙,许春雨,宋建成,等.基于振动模型的采煤机摇臂齿轮局部故障频谱分析[J].工矿自动化,2016,42(7):34-39.
