基于主成分分析法的用电量预测模型

任芳玲,张亚楠

(延安大学 计算机学院，陕西 延安　716000)



基于主成分分析法的用电量预测模型

任芳玲,张亚楠

(延安大学 计算机学院，陕西 延安716000)

摘要：在分析影响陕西省全社会用电量因素的基础上,初步选择第一产业产值、第二产业产值、第三产业产值、能源消费总量、人口自然增长率和城乡居民用电量作为初始变量.利用KMO检验剔除人口自然增长率,之后建立了陕西省全社会电力需求的主成分回归模型,得到主成分后,用MATLAB和SPSS软件对数据进行分析分别选择三次函数模型和幂次函数模型对主成分与社会用电量两个变量进行拟合,得到了较为精准的用电量预测模型.

关键词：KMO检验;主成分分析;拟合;用电量预测

电力是国民经济的命脉,是衡量国家经济水平的重要因素之一.用电量预测是城市发展中一个重要的迫切需要解决的问题,比如2011年席卷全国的“电荒”现象[1],造成停煤缺电、限产限电现象,影响了工业、农业及人们的正常生活.因此,制定科学合理的电力发展规划有益于整个城市的发展,对提高社会经济效益及保证居民正常生活具有至关重要的作用.

影响全社会用电量需求的因素很多,如:政府投入、居民消费水平、市场需求及商品零售价格指数等等,这不单单是用数学模型计算而来,更多的是对其他影响因素的分析[2].电力需求预测有多种方法，陈文静等[3]使用半参数和非参数模型研究了我国电力消费及其影响因素.黄献松等[4]利用ADF检验方法实证分析了陕西省全社会用电量与三大产业之间的关系.多元线性回归分析是统计预测中一个最常用的方法，但是当多个变量之间的相关性较大时，其预测精度会出现较大误差，主成分分析法很好的解决此类问题，所以被广泛应用于税收预测[5]、事故预测[6]等多个方面.本文以陕西省数据为例,将主成分分析法用在用电量预测中.为探索影响陕西省全社会用电量的主要因素,收集了2001—2012年以来的陕西省全社会用电量,基于SPSS软件多元回归分析模型及MATLAB软件拟合函数,建立了预测模型,以期为今后准确预测用电量提供依据.

1变量的选择

1.1变量的初步选择

在查询资料的基础上，初步选取第一产业x1,第二产业x2,第三产业x3,能源消费总量x4,城乡居民用电x5,人口自然增长率x6，用来预测陕西省的电力需求,被解释变量选取陕西省全社会用电量(Y).由《陕西省统计年鉴》获得2001—2012年的全社会用电量及各个因素的统计数据,见表1:

1.2KMO测度对变量的再次选择

在做主成分分析之前应检验所选变量是否具有较强的相关性.KMO测度是SPSS提供判断原始变量间的相关系数大小的一种度量.一个大的KMO测度值支持我们进行主成分分析.

Kaiser给出了常用的KMO度量标准:0.9以上表示非常合适;0.8表示合适;0.7表示一般;0.6表示不太合适;0.5以下表示极不合适.用SPSS软件对表1数据进行KMO检验和Barlett球形检验，得到各个变量间的KMO值是0.784,Barlett球形检验值sig<0.005.可见变量间的相关性一般.为保证得到的主成分能够更好地反映各个变量,因此需要对变量进行剔除.剔变量之前需要用SPSS软件对变量进行相关性分析,得到相关性矩阵,如表2所示:

表1　全社会用电量及各个因素的值

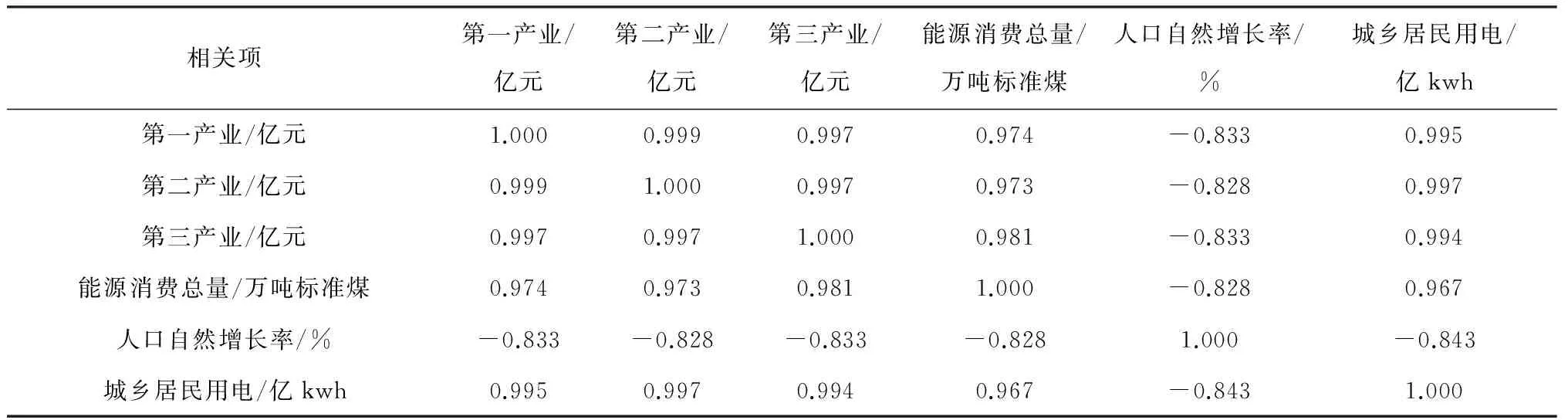
表2　相关性矩阵

由表2相关性矩阵知人口自然增长率与其他变量间的相关系数较低,由此认为人口自然增长率与其他5个变量之间的相关性不大,故将人口自然增长率剔除.

将人口自然增长率剔除后,应用SPSS再次对变量进行KMO检验和Barlett球形检验,此时的KMO值为0.830,sig<0.005,因此这些变量间比较适合做主成分分析.所以选取第一产业产值,第二产业产值、第三产业产值、能源消费总量、城乡居民用电作为分析变量.

2主成分分析原理及模型的建立

2.1主成分分析方法简述

在应用相应变量的时序数据对用电量做预测时,有问题就是变量之间的多重共线性.主成分分析法就是一种解决自变量多重共线性的良好工具.主成分分析方法的基本思想就是对原始变量进行线性组合得到新的综合变量,即主成分.主成分不但保留了原始变量的绝大部分信息,而且彼此之间互不相关.对主成分进行分析,可以抓住主要因素,剔除重叠信息,使问题变得简洁明了.

2.2主成分回归模型的建立

第一产业产值,第二产业产值、第三产业产值、能源消费总量、城乡居民用电,各个变量之间的相关系数较大,存在着较强的相关性.当自变量存在多重共线性时,用最小二乘法得到的回归系数的估计值的方差将会很大,于是估计的精度会降低,这样会影响到回归方程的预测数据的可靠性.接下来的步骤就是为了解决多重共线性的问题.

首先利用SPSS对各个主成分所包含的信息给予解释, 利用主成分分析法，得到第一主成分所解释的总方差为98.989%>95%,故采用第一主成分可认为是充分有效的.

接着用SPSS的主成分分析法做第一主成分的回归系数,得到5个变量第一产业、第二产业、第三产业、能源消费总量、城乡居民用电的系数值分别为0.998、0.998、0.999、0.984、0.996.

进而可得到第一主成分的表达式:

F=0.998x1+0.998x2+0.999x3+0.984x4+0.996x5.

(1)

从第一主成分的表达式来看,5个变量的系数都很接近,说明第一主成分比较均衡地反映了这5个变量的情况.其次根据表1及式(1)得到全社会用电量与第一主成分的值列于表3.

表3　全社会用电量与第一主成分表

使用表3中的相关数据进行曲线拟合,建立因变量Y与第一主成分F的回归模型.

本文在分析数据的特征之后，拟选用三次函数模型和幂次函数模型进行数据拟合.利用MATLAB软件中的cftool命令分别得出两种模型下的拟合表达式为：

三次模型的模型表达式y=a1x3+a2x2+a3x+b,

三次模型的拟合表达式Y=4.6×2.718×10-11×F3- 2.3×2.718×10-6×F2+0.07×F+17.62,

幂次模型的模型表达式y=axb,

幂次模型的拟合表达式Y=0.6485×F0.7306.

为了检验模型预测的准确性大小,这里用所建立模型对数据进行回测,得到通过模型计算得到的社会用电量与其实际用电量之间误差的情况,见表4.

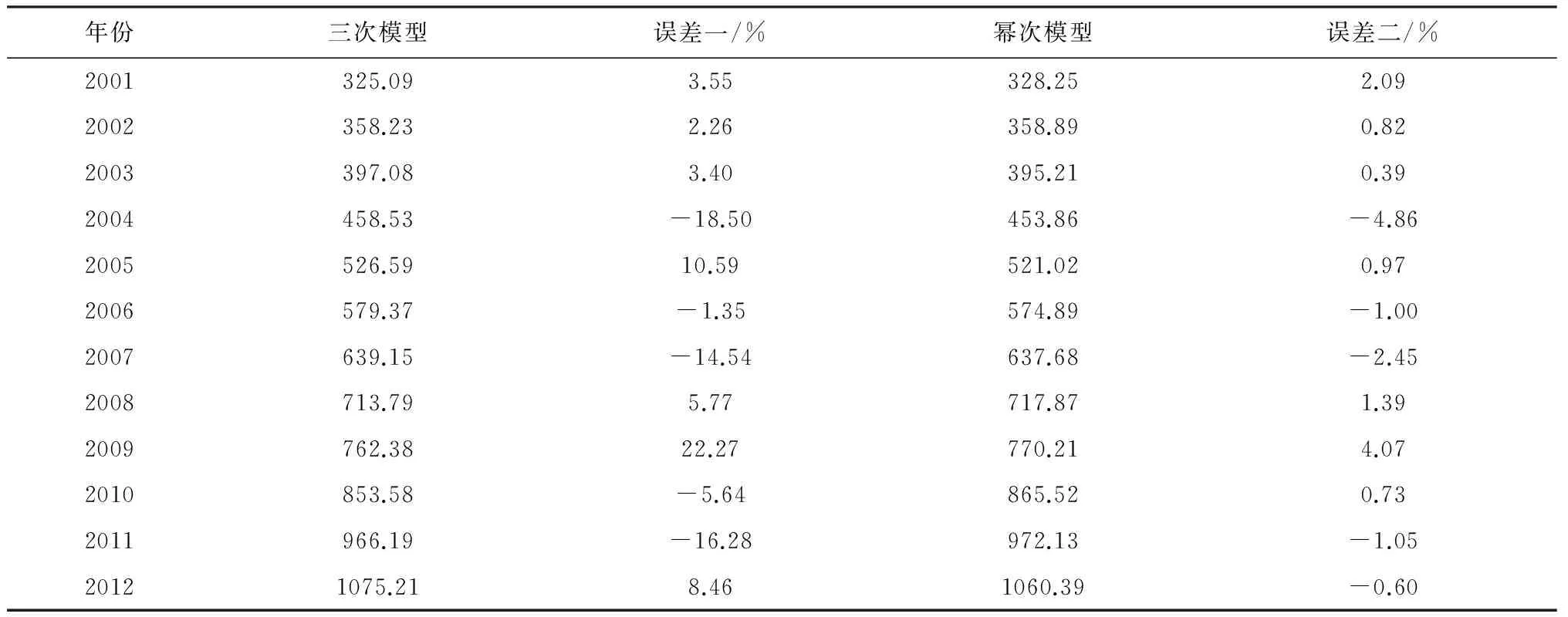
表4　模型的回测值及其与真实值的误差

从表4可知,模型的回测值与实际值较为接近,这说明模型的解释性较强.同时我们还看到,幂次模型误差绝对值最大不超过5%,而三次模型误差绝对值最大达到了18.50%,说明幂次模型与实际值拟合较好.

3结语

通过建立回归模型,得到了陕西省全社会年度用电量与第一产业、第二产业、第三产业、能源消费总量、城乡居民用电的回归预测模型,所得的方程能够用来预测陕西省的年用电量.需要指出的是,各种模型的应用都有它天然的缺陷.对主成分分析模型来说,它只是一种纯统计意义上的模型,在选择主成分的过程中,可能会筛选掉一些经济意义明显但统计意义不明显的变量,而且主成分也没有明显的经济意义.三次模型和幂次模型也有自己的弱点.相对而言,三次模型中数据序列表现得较陡,增加的较快,可能存在高估现象.幂次模型数据序列表现的较符合实际情况.但时序数据预测模型有着共同弱点，如不适当地对产生数据的环境做了一致性假设,并且预期该环境趋势平稳,不会发生较大的改变等,这些隐含假设显然是不现实的.

参考文献：

[1] 查玮.把脉电荒困局——电荒困局症结何在[J].东北电力,2005(8):8-9.

[2] 刘家军,姚李孝,苗华,等.基于SPSS的电力需求与行业发展规律之间的研究[J].现代电力,2010,27(6):83-87.

[3] 陈文静,何刚.电力消费及其影响因素:基于非参数模型的研究[J].系统工程理论与实践,2009(8):92-97.

[4] 黄献松,李邦邦.电能消费与区域经济增长的协整分析[J].西安科技大学学报,2008,28(3):507-512.

[5] 王文臣,汤秀芳.主成分分析法在我国税收预测中的应用[J].信阳师范学院学报(自然科学版),2006,19(4):504-510.

[6] 朱新征,刘志成.基于主成分分析法建立事故预测模型[J].科技创新导报,2009(4):236-239.

(编辑崔思荣)

The Application of Principal Component Analysis in the Electricity Demand Forecasting

REN Fangling,ZHANG Yanan

(College of Computer Science, Yan'an University, Yan'an 716000, China)

Abstract:Based on the analysis of the factors influencing the whole social power consumption in Shanxi province,this paper selected the first,second and third industrial output value,the total energy consumption of urban and rural residents, the natural population growth rate and power consumption as the initial variables.After rejecting the natural population growth rate by KMO test,the principal component regression model of demand for electricity in the whole society in Shanxi province was set up.Then three function models and the exponential function models were chosen on the basis of data analysis by MATLAB and SPSS to fitting two variables of principal component and the power consumption.Finally the more accurate prediction model of power consumption was obtained.

Key words:KMO test; principal component analysis; fitting; plectricity demand forecasting

收稿日期：2016-04-18

基金项目：国家自然科学基金项目(11471007);陕西省教育厅专项科研计划项目(15JK1822);延安大学科研计划项目(YDQ2014-47);延安大学教学改革研究项目(YDJG14-10)

作者简介：任芳玲(1984-)，女，讲师，硕士，主要从事金融数学和概率统计的研究.

中图分类号：TP391.4

文献标志码：A

文章编号：1674-358X(2016)02-0050-04