土岩复合地层中地铁施工Peck沉降预测公式改进

姚爱军，卢　健，邱忠旺，王文森，蔡长欣（北京工业大学城市与工程安全减灾教育部重点实验室，北京　100124）



土岩复合地层中地铁施工Peck沉降预测公式改进

姚爱军，卢健，邱忠旺，王文森，蔡长欣
（北京工业大学城市与工程安全减灾教育部重点实验室，北京100124）

摘要城市地铁暗挖施工中，预估地表沉降方法中应用最广泛的是Peck公式法，但其适用条件具有一定的局限性。为此，针对土岩复合地层条件下长春地铁一号线双线隧道暗挖工程地表沉降的部分监测数据，应用一元线性回归方法，采用对单条隧道的沉降数据分别拟合再叠加的方法获得了双线隧道的实测数据拟合曲线。将实测数据拟合曲线与Peck公式预测曲线对比，对Peck公式中的沉降槽宽度和地表最大沉降量进行修正，得出适用于本地区双线隧道施工的Peck修正公式。研究表明:修正后的Peck公式中沉降槽宽度修正系数主要分布在0. 5～0. 9、地表最大沉降量修正系数主要分布在0. 3～0. 8，修正后的Peck公式预测沉降曲线与实测数据拟合曲线吻合良好，可作为研究区地表沉降预测方法。

关键词土岩复合地层；地铁隧道；Peck公式；修正系数

预估地铁隧道开挖引起的地表沉降变形方法中应用最广泛的就是Peck公式法。Peck于1969年定义了地层损失的概念，然后提出了预估隧道开挖引起的地表沉降变形的方法，他认为地表沉降槽近似正态曲线分布，并且沉降槽体积与地层损失体积相等［1］。韩煊等［2］针对全国各地搜集到的30多组实测沉降变形数据进行研究，得出了若隧道埋深达到一定深度，其瞬时地表沉降曲线符合高斯分布。陈春来等［3］针对双线盾构隧道施工引起地表沉降进行了数值模拟计算，得出在两条隧道间距较小情况下，地表沉降符合正态分布；若隧道间距较大，则地表沉降槽形状由Ⅴ形转变为W形。李倩倩等［4］认为当两条隧道轴线间距＜2D（D为隧道直径）时，地表沉降呈单凹槽状，间距＞2D时呈双凹槽状。姚爱军等［5］对大间距双线隧道矿山法地铁施工引起的地表沉降进行了研究，得出了在两条隧道开挖交叉影响区域内地表沉降会叠加，大间距隧道施工对另外一条隧道影响较小。任强等［6］认为Peck公式对双线平行隧道适用，且隧道开挖引起的地表沉降呈两个正态分布地表沉降槽叠加，地表沉降槽沿两条隧道轴线距离中点呈轴对称分布。刘波等［7］根据研究得出了相距不远的两条隧道在开挖过程中会对地表沉降槽产生相互叠加的影响，并且根据叠加原理给出了双线隧道开挖地表沉降预测公式

式中：l为两条隧道中心距，且坐标原点取在两条隧道轴线对称中心位置。

由于各地区地层差异，导致各个地区的地表变形实测值与Peck公式预测值差异较大，因此Peck公式具有局限性。鉴于此，姚爱军等［8］针对北京地区地铁隧道的Peck沉降预测公式进行了修正，修正后的Peck公式预测的沉降槽曲线与实际沉降曲线吻合较好。杨清源等［9］对大连地铁隧道施工实测数据进行分析，得出了适用于大连地铁部分地区的修正Peck沉降预测公式。段绍伟等［10］针对长沙地区地铁开挖实测数据进行了回归分析，并对Peck沉降预测公式进行了修正，修正结果符合长沙地区地铁施工引起的地表沉降规律。

本文基于长春地铁一号线双线隧道暗挖段地表沉降监测数据，引入地表最大沉降量修正系数α和沉降槽宽度修正系数β，对Peck公式进行修正，得出的结果为本地区地表沉降预测提供参考。

1　工程概况

长春市地铁1号线解放大路站～自由大路站区间处于长春市人民大街正下方。解放大路站～自由大路站区间隧道起始于解放大路站南端，沿人民大街道路下方布置，向南依次下穿环形永昌路、义和路等最后进入自由大路站。区间沿线地面高程215. 28～208. 43 m，区间线路纵向呈一面坡形式，隧道纵坡坡度为4‰，区间隧道顶埋深16. 1～20. 8 m。区间隧道采用暗挖法施工，本区间的设计里程为K19 + 471. 700—K20 + 827. 200，区间长度约为1 355. 5 m。设置一处临时施工竖井，中心里程为K20 + 294. 073，于K19 + 925处设置联络通道，临时竖井及横通道作为另外一个联络通道使用。区间范围内的地层由上到下依次为杂填土、粉质黏土、砾砂、全风化泥岩、强风化泥岩、中风化泥岩。隧道处于土岩复合地层，断面形状为马蹄形断面，开挖净空为6. 5 m（高）×6. 2 m（宽），采用超前小导管进行超前支护，洞内开挖采用机械配合人工开挖，短台阶法施工。

2　实测数据回归分析

2. 1回归分析原理Peck公式为

式中：S（x）为距离隧道轴线x处地表沉降，m；Smax为地表最大沉降量，mm；i为沉降槽宽度，m；x为沉降监测点到隧道轴线的距离，m。

首先对Peck公式两边同时取对数可以得到

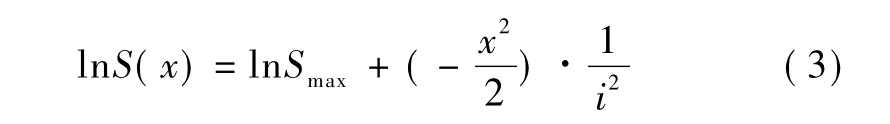
以lnS（x）和- x2/2为变量，以lnSmax为常数项，以1 /i2为线性系数，进行以下回归分析。

式中：xj项为第j个沉降监测点与隧道轴线之间的距离，n为样本数量，）a为回归后的常数项，）b为回归后的线性系数。

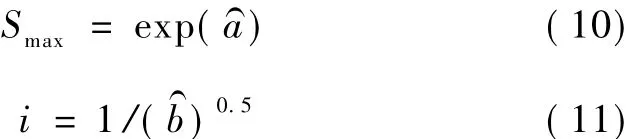
由公式（2）到公式（11）可以得到回归后的Smax及i，即可得到回归曲线。

采用线性相关系数R检验回归函数的线性相关关系。

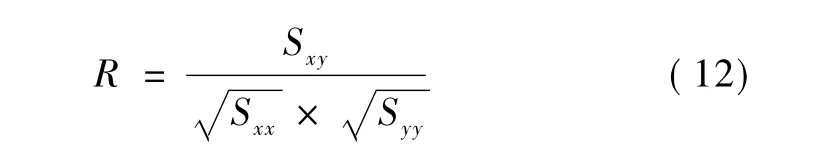
当R＞r0. 01（n - 2）时，回归函数的线性关系高度显著；当r0. 01（n - 2）＞R＞r0. 05（n - 2）时，回归函数的线性关系显著。

2. 2实测数据回归分析

由于本区间隧道为两条隧道开挖施工，且两条隧道距离较近，故本文采用公式（1）作为预测地表沉降公式。由于双线隧道开挖引起的地表沉降量是单条隧道分别开挖引起的地表沉降量的叠加，且本文中沉降监测点主要分布在左线隧道轴线的左侧和右线隧道轴线的右侧，一条隧道开挖对另一条隧道监测点的影响较小。所以本文对两条隧道的沉降预测公式先分别修正，再进行叠加，并且偏安全考虑，在对单条隧道的沉降预测公式进行修正时认为两条隧道远离对称轴侧监测所得沉降数据是由于单条隧道开挖所引起，忽略另外一条隧道产生的影响。

根据回归分析原理选取左线的一个监测断面进行分析，将xj为- 7，- 4，- 2，0，7，S（x）为- 7. 32，- 9. 21，- 9. 30，- 10. 52，- 7. 06依次代入公式（4）～公式（6）可得Sxx为572. 3，Syy为0. 116 88，Sxy为7. 982。根据公式（7）、公式（8）得到）a为2. 312 58，）b为0. 013 947 2。则回归后的线性函数为

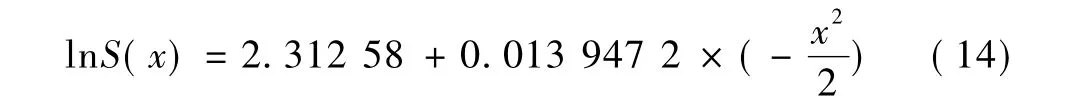
线性相关系数R为0. 975，相关系数临界值r0. 01（3）为0. 959，因此可以认为回归方程的线性关系高度显著。左线线性回归结果见图1。

从图1中可以看到，实测数据均匀地分布在拟合回归曲线两侧，因此拟合结果良好。

将）a，）b代入公式（10）、公式（11）可求得Smax为10. 10 mm，i为8. 46。从而可以得到拟合后的左线沉降曲线。

同理选取同一监测断面右线进行分析，将xj为- 7，0，2，4，7，S（x）为- 7. 41，- 12. 45，- 10. 41，- 9. 10，- 6. 76依次代入公式（4）～公式（6），可得Sxx为572. 3，Syy为0. 246 1，Sxy为11. 409 0。根据公式（7）、公式（8）得到）a为2. 431 233，）b为0. 019 935。则得到回归后的线性函数为

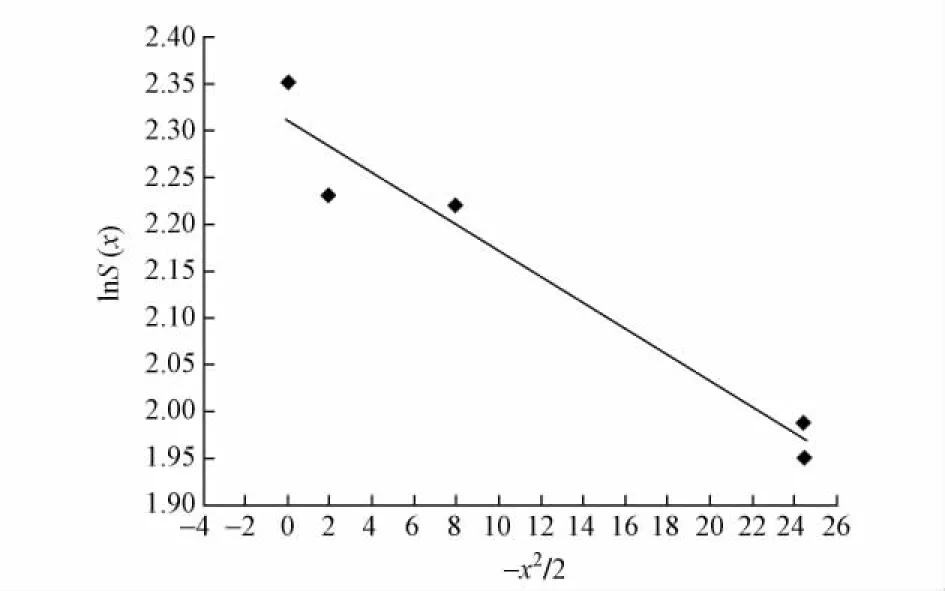
图1　左线回归拟合结果

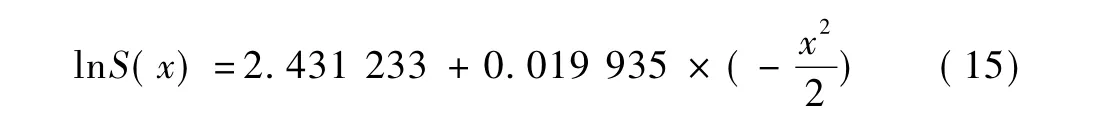
线性相关系数R为0. 961，相关系数临界值r0. 01（3）为0. 959，因此可以认为回归方程的线性关系高度显著。右线线性回归结果见图2。

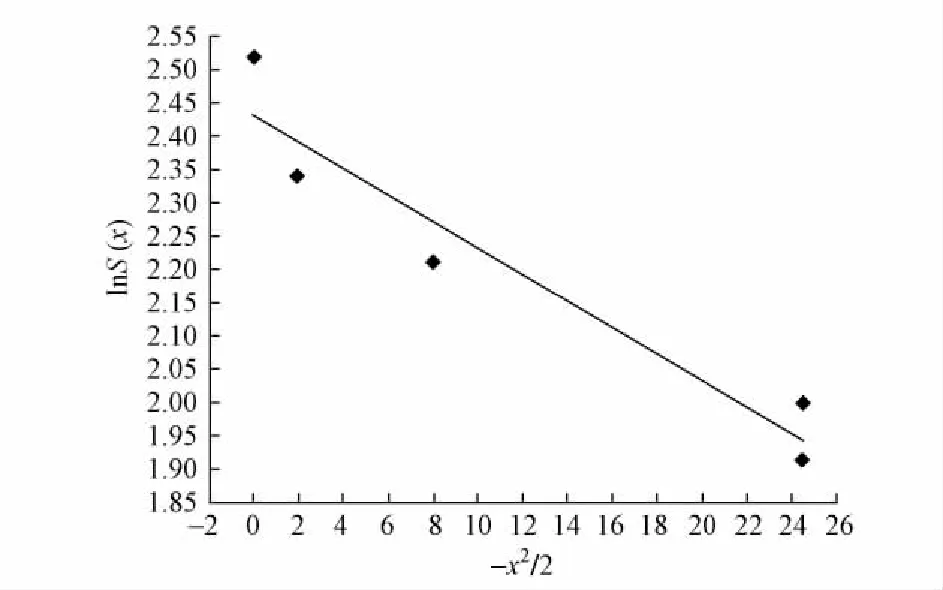
图2　右线回归拟合结果

从图2中可以看到，实测数据均匀地分布在回归曲线两侧，因此拟合结果良好。

将）a，）b代入公式（10）、公式（11）可求得Smax为11. 37 mm，i为7. 08。从而可以得到拟合后的右线沉降曲线。

将拟合后的左线和右线沉降曲线进行叠加，将叠加后的结果和Peck公式预测沉降曲线对比于图3。

由图3可以看出，Peck公式预测的沉降曲线与实测数据拟合曲线相差较大。这一差异主要是由于不同地区地层条件不同、施工方法不同所致。为了能够更好地发挥Peck公式的优点，更好地指导本地区施工，需要对Peck公式进行修正。

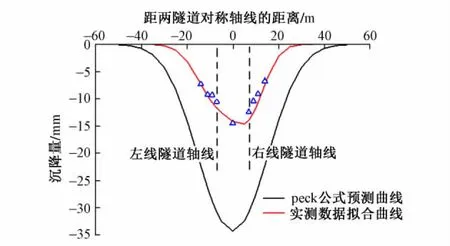
图3　Peck公式预测曲线与实测数据拟合曲线对比

3 Peck公式改进

本文引入地表最大沉降量修正系数α和沉降槽宽度修正系数β对Peck公式进行修正。修正后的Peck公式为

将公式（16）分为左线和右线先分别考虑再叠加，并取两条隧道轴线为坐标原点，对公式两边取对数，可得公式（17）、公式（18）。

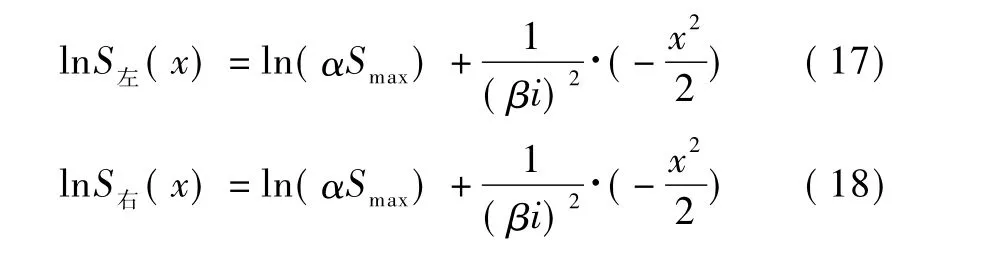
运用第2节实测数据回归分析求得的）a左，）b左和）a右，）b右。结合公式（9）、公式（10）可以得到α= exp（）a）/ Smax，β= 1 /［i（）b）0. 5］，其中Smax，i由Peck公式计算求得。可以得到α左为0. 51，β左为0. 66，α右为0. 57，β右为0. 56。

将施工过程中监测的59个断面实测数据按照以上方法进行回归分析并对Peck公式进行修正。因为左线隧道和右线隧道关于两条隧道轴线距离中点呈轴对称分布，所以将左线的修正系数和右线的修正系数一起加以分析。α，β分布见图4。

由图4可以看出，α主要分布在0. 3～0. 8，占79. 66％。β主要分布在0. 5～0. 9，占97. 46％。由此可以得出，对于土岩复合地层条件下地铁双线暗挖隧道，地表最大沉降量修正系数α在0. 3～0. 8，沉降槽宽度修正系数β在0. 5～0. 9，Peck公式预测的地表沉降槽曲线可以较好符合本地区实际沉降槽曲线。

对典型断面的Peck公式（公式（1））进行修正，修正系数取平均值，α为0. 55，β为0. 7，得到修正后曲线。取α为0. 3，β为0. 5可得修正后的上限曲线，取α为0. 8，β为0. 9可得修正后的下限曲线。将修正后上限曲线、下限曲线、典型断面Peck公式修正后预测曲线、实测数据拟合曲线进行对比，见图5。可见，实测数据拟合曲线、Peck公式修正后预测曲线均在上下限之间，并且实测数据拟合曲线与Peck公式修正后预测曲线相差较小，修正结果较为合理。

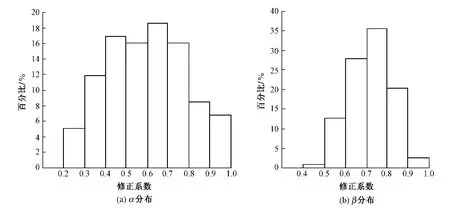
图4　地表最大沉降量修正系数α和沉降槽宽度修正系数β的分布

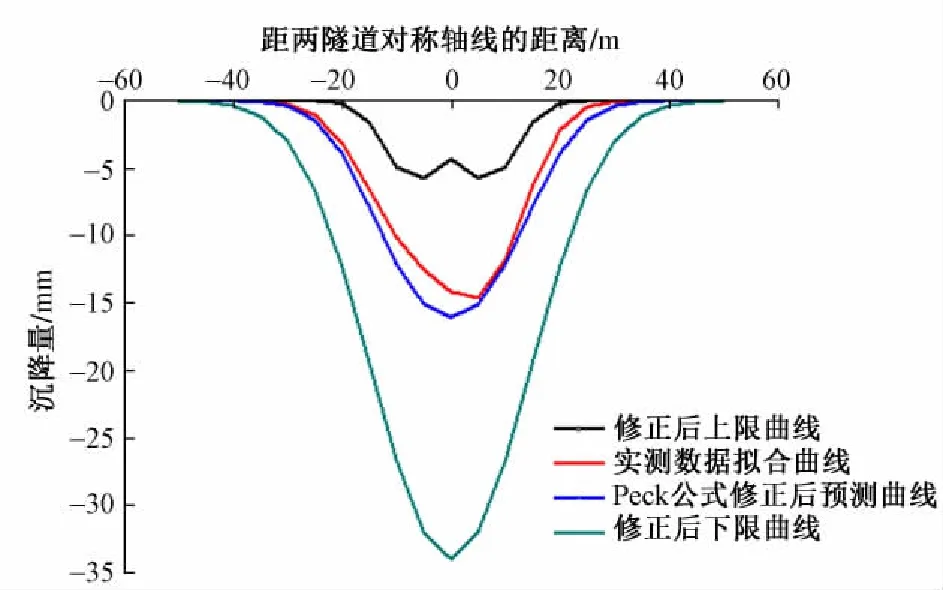
图5　Peck公式修正后预测曲线与实测数据拟合曲线对比

4　结论

本文对长春地铁一号线地铁双线暗挖隧道工程地表沉降实测数据进行了回归分析，获得了地表沉降曲线。由于Peck公式受不同地区地质情况影响较大。本文引入地表最大沉降量修正系数α和沉降槽宽度修正系数β对Peck公式进行了修正，得出地表最大沉降量修正系数α主要分布在0. 3～0. 8、沉降槽宽度修正系数β主要分布在0. 5～0. 9，修正后的Peck公式预测的地表沉降曲线与实测数据拟合曲线吻合较好。

本文得出的结果只适用于本工程，具有一定的局限性，其他地区还有待对当地实测数据进一步研究。

参考文献

［1］Peck R B. Deep Excavations and Tunnelling in Soft Ground ［C］/ /Proceedings of the 7th International Conference on Soil Mechanics and Foundation Engineering. Mexico，1969：225-290.

［2］韩煊，李宁，STANDING J R. Peck公式在我国隧道施工地面变形预测中的适用性分析［J］.岩土力学，2007，28（1）：23-28.

［3］陈春来，赵城丽，魏纲，等.基于Peck公式的双线盾构引起的土体沉降预测［J］.岩土力学，2014，35（8）：2212-2218.

［4］李倩倩，张顶立，房倩，等.浅埋暗挖法下穿既有盾构隧道的变形特性分析［J］.岩石力学与工程学报，2014，33（增2）：3911-3918.

［5］姚爱军，管江，赵强，等.大间距双线地铁隧道矿山法施工引发地表沉降的规律［J］.岩土工程界，2009，12（4）：34-37.

［6］任强，杨春英，徐薇.地表沉降的双洞体叠加Peck公式及数值分析［J］.安徽理工大学学报（自然科学版），2013，33 （4）：78-82.

［7］刘波，陶龙光，丁城刚，等.地铁双隧道施工诱发地表沉降预测研究与应用［J］.中国矿业大学学报，2006，35（3）：356-361.

［8］姚爱军，赵强，管江，等.基于北京地层地铁隧道施工的Peck公式的改进［J］.地下空间与工程学报，2010，6（4）：789-793.

［9］杨清源，麻凤海，胡国栋，等.大连地铁隧道施工的Peck公式改进［J］.辽宁工程技术大学学报（自然科学版），2012，31（2）：159-162.

［10］段绍伟，黄磊，鲍灶成，等.修正的Peck公式在长沙地铁隧道施工地表沉降预测中的应用［J］.自然灾害学报，2015，24（1）：164-169.

（责任审编葛全红）

Improving of Peck's Settlement Calculation Formula Related to Metro Tunnel Construction in Soil-Rock Composite Stratum

YAO Aijun，LU Jian，QIU Zhongwang，WANG Wensen，CAI Changxin
（Key Laboratory of Urban Security and Disaster Engineering，Ministry of Education，Beijing University of Technology，Beijing 100124，China）

AbstractAs for city metro excavation constructions，the peck formula is widely used for surface subsidence prediction，but it still has its limitation. A case study was conducted in this paper. T he settlement of Changchun twoline metro tunnel passing soil-rock composite stratum was monitored. W ith linear aggression，the settlement of a single tunnel was fitted and superposition was then used to obtain the two-line settlement. T he actual data were compared with the predicted curve using peck formula. T he settler width and the maximum surface settlement were corrected；thus，the improved peck formula can be effectively applied. T he correction factor for settler width is between 0. 5 and 0. 9，and that for maximum surface settlement is between 0. 3 and 0. 8. T he predicted settlement curve using the improved peck formula fits well with the measured data.

Key wordsSoil-rock composite stratum；M etro tunnel；Peck formula；Correction factor

中图分类号U455. 4

文献标识码A

DOI:10. 3969 /j. issn. 1003-1995. 2016. 06. 23

文章编号：1003-1995（2016）06-0083-05

收稿日期：2015-10-20；修回日期：2016-04-25

基金项目：高等学校博士学科点专项科研基金（20121103110022）；国家自然科学基金（51578023）

作者简介：姚爱军（1966—），男，教授，博士。