铁路大跨度钢管混凝土系杆拱桥设计计算

王淑敏（铁道第三勘察设计院集团有限公司桥梁处，天津　300142）



铁路大跨度钢管混凝土系杆拱桥设计计算

王淑敏
（铁道第三勘察设计院集团有限公司桥梁处，天津300142）

摘要以某铁路大跨度钢管混凝土拱桥为工程背景，在详述该结构构造形式及结构尺寸的基础上，利用有限元程序对系梁、拱肋、吊杆等结构关键部位及结构整体进行了受力及变形分析，以期验证结构形式和结构尺寸的合理性。通过计算分析验证了该桥结构设计合理，受力变形满足规范要求。同时也可为类似桥梁设计提供参考。

关键词钢管混凝土；系杆拱；有限元；动力特性

1　工程概况

某铁路桥主桥上部结构采用1-95. 7 m钢管混凝土系杆拱，全长98 m，平面位于线路直线段及缓和曲线段，立面位于平坡及坡度- 1. 2‰的纵坡上。桥面纵坡通过拱肋与系梁刚性旋转实现，系梁统一采用坡度- 0. 98‰的纵坡，保证两侧梁端和梁顶的标高不变，调整其余部位系梁梁顶道砟厚度，以满足线路纵坡要求。吊杆垂直梁面布置。拱桥立面图如图1所示。

图1　95. 7 m钢管混凝土简支拱桥立面（单位：cm）

2　系杆拱结构构造

1）拱肋

系杆拱全长98 m，计算跨度为95. 7 m，矢跨比为f/L = 1∶4. 984，拱肋立面投影矢高19. 2 m，拱肋采用二次抛物线。拱肋在横桥向内倾8°，形成提篮式样。

拱肋横断面采用哑铃形钢管混凝土等截面，截面高度h = 2. 5 m，钢管直径为1 m，由厚20 mm的钢板卷制而成，拱管内灌注C50补偿收缩混凝土。

2）横撑

拱肋之间设1道一字撑和4道K撑。一字撑采用外径1. 0 m的圆形钢管组成，斜撑采用外径0. 8 m的圆形钢管组成，钢管内均不填充混凝土。

3）吊杆

吊杆采用OVM TES（FD）7-121成品索，平行布置，除D1和D2（D1'和D2'）间距为4 m外，其余吊杆间距均为5 m，全桥共设17对吊杆，吊杆纵向垂直梁面布置，在横向内倾8°。

4）系梁

系梁采用单箱三室预应力混凝土箱形截面，跨中梁高2. 50 m，端部梁高3. 05 m。梁部桥面板宽17. 5 m，底板宽14. 9 m，梁部断面图见图2。混凝土等级为C50。

3有限元分析模型的建立

本桥整体模型采用空间有限元程序MIDAS/ CIVIL计算，按照规范及设计标准进行动静荷载加载，列车荷载采用中-活载。主桥采用梁单元建立模型进行分析。

采用梁单元建模时，对于系梁、拱肋及横撑的各杆件采用三维梁单元进行模拟，其截面特性按照实际设计截面定义。拱轴线为二次抛物线，拱肋采用哑铃形截面，钢管和腹杆内均填充混凝土（为等截面），采用“双单元、共节点”的方法模拟钢管混凝土拱肋。吊索采用桁架单元模拟，仅考虑其轴向的拉伸刚度。整体模型如图3所示。

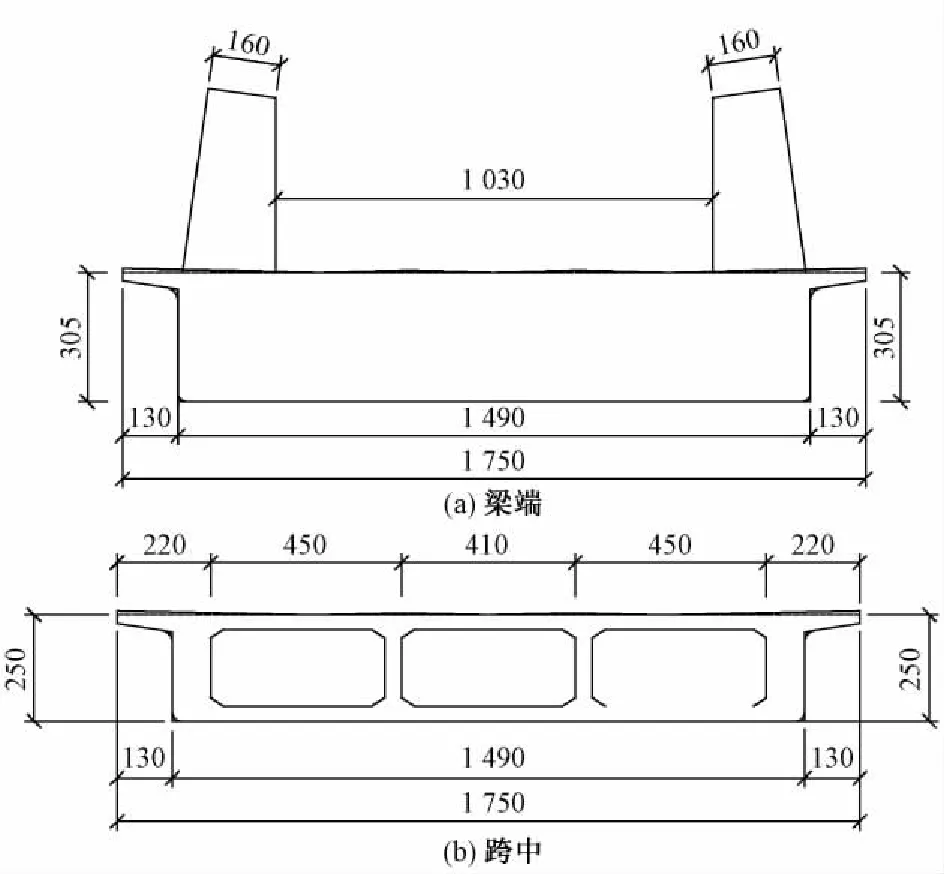
图2　梁部断面（单位：cm）

图3　全桥有限元模型

4　全桥计算分析

4. 1系梁强度和应力

4. 1. 1正应力

最不利荷载工况下各截面正应力见图4和图5（正号表示拉应力，负号表示压应力，下同）。

4. 1. 2主拉应力和主压应力

最不利荷载工况下各截面主拉应力和主压应力见图6。

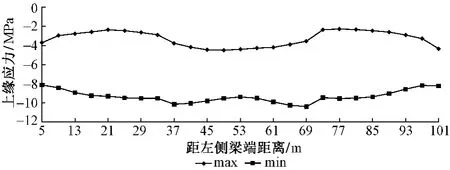
图4　最不利荷载组合下梁部截面上缘应力

图5　最不利荷载组合下梁部截面下缘应力

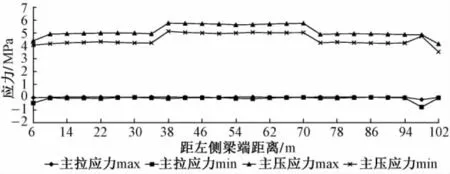
图6　最不利荷载组合下梁部截面主应力

4. 1. 3抗裂性检算

梁部控制截面抗裂性检算结果见表1。可见，抗裂安全系数K＞1. 2。

4. 1. 4剪应力

运营荷载作用下，梁部各截面剪应力见图7。

表1　梁部控制截面抗裂性检算结果

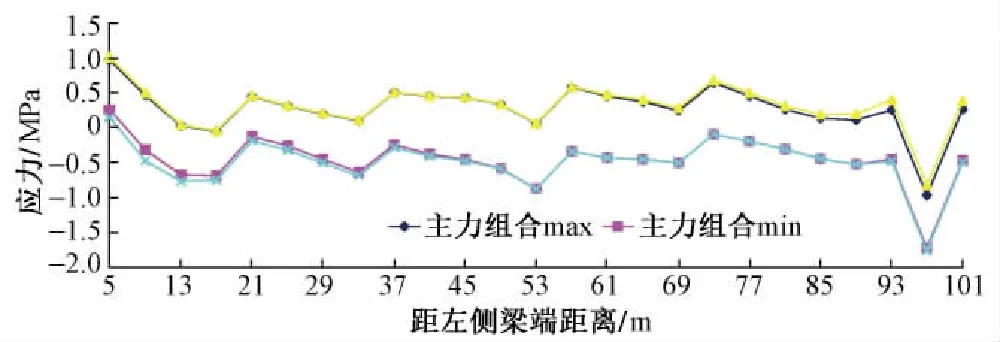
图7　运营荷载作用下梁部截面剪应力

4. 2拱肋应力

最不利荷载组合下拱肋钢管及混凝土的最大正应力见表2。

表2　拱肋截面最大正应力计算结果　MPa

4. 3吊杆

各荷载组合下吊杆应力计算结果如表3所示。

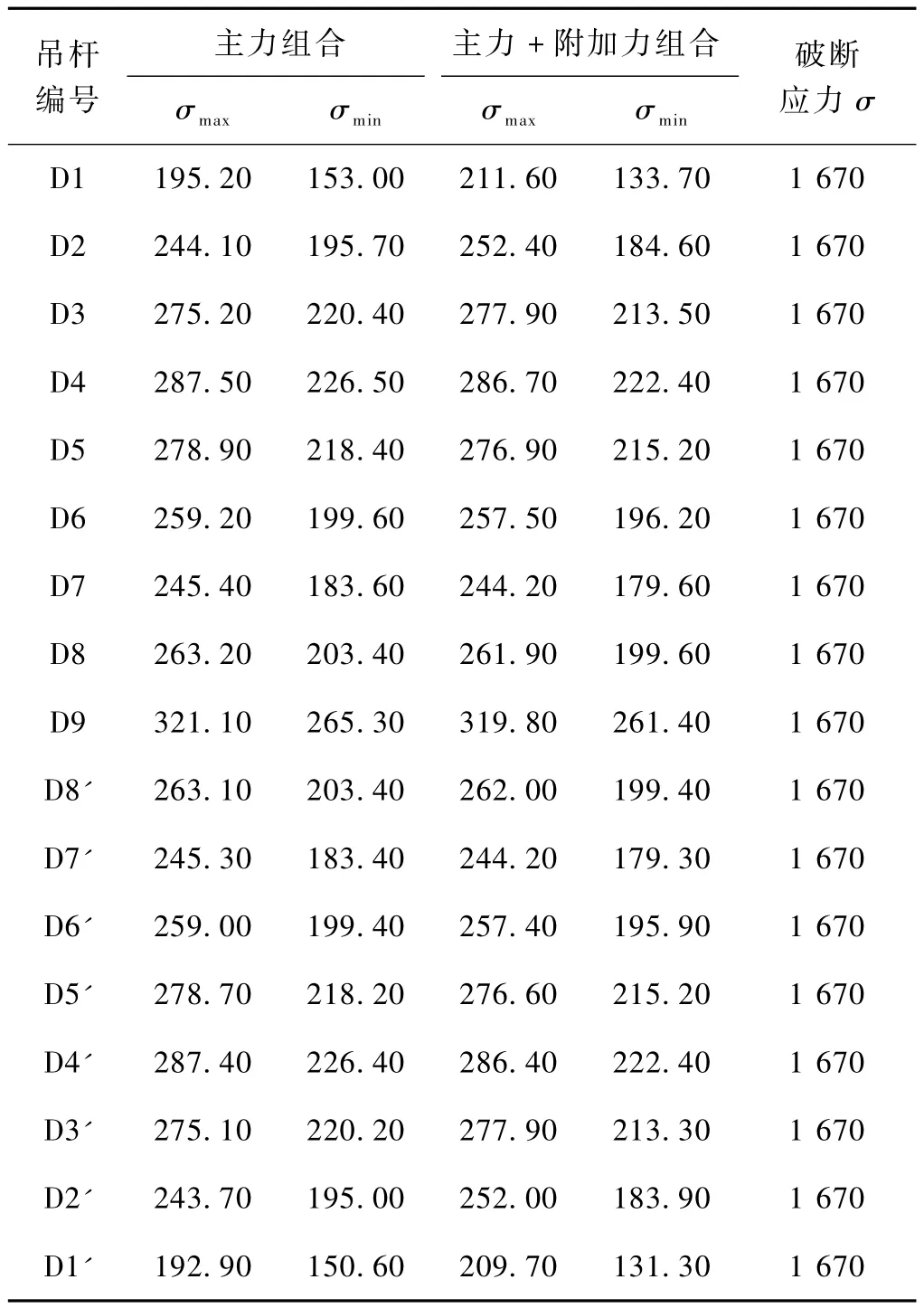
表3　吊杆应力组合计算结果　MPa

4. 4全桥动力特性分析

根据三维有限元模型，对全桥进行了动力特性分析，分析结果：

横向一阶模态，自振周期0. 700 s，频率1. 429 Hz。

竖向一阶模态，自振周期0. 143 s，频率6. 996 Hz。

扭转一阶模态，自振周期0. 350 s，频率2. 861 Hz。

4. 5拱肋稳定分析

4. 5. 1拱肋面内的稳定性

拱肋面内的稳定性按承受最大水平推力的中心受压杆件进行检算。经检算拱肋面内稳定安全系数计算值为6. 30＞5，满足规范要求。

4. 5. 2拱肋面外的稳定性

计算时，模型考虑活载效应，屈曲模态见表4及图8。

表4　拱肋面外稳定性计算结果

图8　屈曲模态五透视图（竖向及横向侧倾）

5　结语

本文以某铁路大跨度钢管混凝土系杆拱桥为研究对象，以三维有限元为研究方法，建立了该桥全桥有限元模型，并在此基础上对主梁、拱肋、吊杆等结构关键部位及全桥进行了应力、变形、动力特性及稳定性检算。结构各项指标均满足规范要求，既验证了结构设计的合理性，又可为同类铁路大跨度钢管混凝土拱桥的设计与研究提供借鉴。

参考文献

［1］陈宝春.钢管混凝土拱桥［M］.北京：人民交通出版社，2007：30-42.

［2］过镇海，时旭东.钢筋混凝土原理和分析［M］.北京：清华大学出版社，2003：64-77.

［3］王召祜.客运专线桥梁设计研究［J］.铁道标准设计，2005（4）：42-44.

［4］李杰，陈淮，江莹莹，等.钢管混凝土系杆拱桥吊杆力计算及调索方法研究［J］.铁道建筑，2014（1）：7-10.

［5］朱伯芳.有限单元法原理与应用［M］. 2版.北京：水利水电出版社，1998：32-44.

［6］中华人民共和国建设部. GB 50010—2002混凝土结构设计规范［S］.北京：中国建筑工业出版社，2002.

［7］中华人民共和国铁道部. TB 10002. 3—2005铁路钢筋混凝土及预应力混凝土结构设计规范［S］.北京：中国铁道出版社，2005.

［8］肖汝城，陈红，魏乐永.桥梁结构体系的研究［J］.土木工程学报，2008，41（6）：69-74.

（责任审编孟庆伶）

Design Calculation of Railway Long-span Concrete-filled Steel Tube Tied Arch Bridge

WANG Shumin
（Bridge Design Department，The Third Railway Survey and Design Institute Group Corporation，Tianjin 300142，China）

AbstractA railway large-span concrete-filled steel tube arch bridge was studied in this paper. Its structure and size were introduced. W ith finite element method，both global and local responses were evaluated to validate the rationality of design. T he key components including spring-beam，arch and suspension rod were analyzed. T he calculation results show that the strength and the deformation meet the requirements of relevant codes.

Key wordsConcrete-filled steel tube；T ied arch；Finite element；Dynamic characteristic

中图分类号U448. 22+5

文献标识码A

DOI:10. 3969 /j. issn. 1003-1995. 2016. 06. 05

文章编号：1003-1995（2016）06-0019-04

收稿日期：2016-01-22；修回日期：2016-03-28

作者简介：王淑敏（1972—），女，高级工程师。