GARCH族模型在电力市场电价预测中的比较研究

刘丽燕，邹小燕



GARCH族模型在电力市场电价预测中的比较研究

刘丽燕，邹小燕

(重庆师范大学经济与管理学院，重庆 401331)

电力市场电价的剧烈波动存在巨大的风险。准确的电价预测有助于市场参与者管理风险并达到自身利益的最大化。用ARMA—GARCH族模型对美国PJM电力市场和北欧电力市场的日前小时电价序列进行建模和预测。在模型估计时假设残差分别服从正态分布和学生t分布，进而比较不同模型对不同电力市场日前电价的预测精度。通过比较得出，非对称的GARCH模型预测效果较好。但ARMA—GARCH族模型不适用于波动异常剧烈、电价序列间相关性较弱的电力市场，并以澳大利亚电力市场电价数据为例进行了分析。

电力市场；电价预测；GARCH族模型

0 引言

在电力工业改革之前，电价由政府相关部门统一制定，短期内电价较为稳定，波动较小。政府放松管制之后，电力市场的电价由供需双方来决定，并受到天气、系统负荷、输电网络阻塞等客观因素的影响，使得电力市场中电价经常显示出价格尖峰等特征[1-2]，这加大了电价预测的难度，并给电力市场参与者带来极大的市场风险。因此，对电价进行精准的预测显得尤为重要。

电价预测的重要性及复杂程度使很多学者在这个领域开展了大量研究[3-7]。电价序列中相邻时段的电价具有较强的相关性，ARMA模型则是利用这种电价间的联系来预测下一个时段电价。但是简单的ARMA模型的预测精度并不高，并且电价存在异方差性，GARCH族模型针对该特性进行建模，很好地拟合了电价波动的异方差性，提高了预测精度[8]。针对电价序列的波动特征，采用ARMA模型与ARCH模型[9]或者GARCH模型结合的方法[10]对电价的均值和波动性进行建模较多，且精确性较高。文献[11]较早运用ARMA-GARCH模型预测北欧电力市场的电价，着重研究的是电价的均值回归和异方差性，使用的是比较单纯的ARMA-GARCH模型。文献[12]采用ARMA模型与GARCH族模型以及均值GARCH(GARCH-M)族类模型进行短期电价预测。文献[13]运用EGARCH模型来处理电价数据的负杠杆效应，提出加入方差扰动项的EGARCH-M模型，并用MISO电力市场数据证明了杠杆效应的存在。GARCH族类模型有较少的变量，并且可以很好拟合电价的时变方差。

针对电价序列的波动特征，本文用ARMA- GARCH族模型对日前小时电价进行建模，通过对残差做不同分布的假设比较ARMA-GARCH族模型在不同电力市场中的预测精度。本文结构如下：第一部分是实证数据分析；第二部分是实证模型的建立；第三部分是GARCH族模型的估计结果和预测精度；第四部分是GARCH族模型的适用性讨论；第五部分是结论。

1 实证数据分析

自19世纪80年代以来，世界上很多国家开始重建电力工业，其目的在于打破垄断、引入公平竞争和提高经济效率。这促进了电力市场的形成和逐步完善。本文选取北欧电力市场和美国PJM这两个比较成熟的电力市场进行分析。

北欧电力市场(包括了芬兰、拉脱维亚和立陶宛等7个国家)是世界上最大的日前电价交易市场，在北欧地区以及波罗的海一带具有较高的透明度、流动性和安全性。市场电价数据包括系统电价和区域电价两部分。由于各个节点地区的传输能力和区域间的传输阻塞情况不同，各点地区的电价就形成了该地区的区域电价。北欧电力市场中，电力需求量最大和需求量最小的分别是苏丹(SE)和爱沙尼亚(EE)两个节点区域。本文选取北欧电力市场的系统小时电价，以及SE和EE两个节点的小时电价进行分析。

美国PJM市场(包括了宾夕法尼亚州、纽泽西州、马里兰州和特拉华州等13个州及哥伦比亚特区)的规模目前处于世界第三位，有日前电价市场和实时电价市场两部分。PJM电力市场是用本地边际电价来反应特定时间和地区的电价。本文所用电价数据来源于日前电价市场，日前电价市场是一个期货市场，该市场中在安排供应、需求报价和双边交易的基础上计算下个交易日的小时电价。

以上两个市场电价均为每小时竞价一次，故所用电价数据为日前小时电价，每天有24个电价数据。本文在对以上市场的电价数据进行研究时，选取2012年1月1日到2013年12月31日的电价，共17 544个电价数据进行建模，并用2014年1月1日至2014年12月20日，共8 496个电价数据来检验模型的预测精度。

对四组电价数据进行分析时发现，由于需求受到季节以及日常活动的影响，电价有时会出现一些极大的正负偏离，这种极端的正负偏离已经不属于“正常”波动，一般称为电价的“极值跳跃”。对电价序列进行统计分析发现电价序列存在超额峰度，峰度值从24.614到83.721(见表1)，并有较厚的尾部特征，则电价序列存在“尖峰”“厚尾”的特征。同时电价序列常常表现出“波动率聚集性”，即电价序列的波动(即方差)往往表现出大的波动后面跟随大的波动，小的波动后面跟随小的波动，从而表明电价序列存在异方差性。在金融市场，资产收益率存在杠杆效应，即负的波动比正的波动对波动率的影响更大。而在电力市场中表现为，正的波动比负的波动对波动率的影响大，即存在负的杠杆效应。表1为对四个组电价数据的描述性统计。

表1 数据描述性统计

注：样本是从2012年1月1日到2014年12月20日

2 实证模型建立

ARMA-GARCH族模型的优点在于该模型能很好地刻画电价的波动剧烈、波动率聚集等特征，特别适用于波动性的分析和预测。其中加入门限值和非对称项的GARCH族模型(TGARCH、EGARCH、APARCH和CGARCH)能很好地拟合电价波动的负杠杆效应[14]。

ARMA-GARCH族模型是对平稳的时间序列建模的方法，在对以上四组电价数据进行建模之前，首先需要检验电价序列的平稳性。在Eviews7.0中检验办法有ADF和PP等六种。本文用ADF检验方法对四个市场数据进行单位根检验，结果显示四个电力市场数据均不存在单位根，即电价序列平稳。

在建立ARMA模型时考虑到电价序列的波动性特征，对四组电价数据的自相关和偏自相关函数观察发现一周内同一时点的电价与当前时点电价相关性显著，所以在ARMA模型中加入24阶、48阶、72阶、96阶、120阶、144阶和168阶滞后项。在EE和SE市场中，2阶滞后项系数显著不为零。对于北欧电力市场系统电价分析可知， 2阶和4阶滞后项系数显著不为零。而在PJM电力市场中，则是5阶滞后项系数显著不为零。根据AIC信息准则，对SE和EE两个市场建立如下ARMA模型。

对北欧电力市场的系统电价建立如下ARMA模型。

(2)

对PJM市场的日前小时电价建立如下ARMA模型。

采用最小二乘法对ARMA模型进行估计得出四组市场数据的拟合优度均高于70%，根据AIC信息准则判断上述模型表现较好。

由于残差序列之间的相关度较低，并考虑参数的节俭原则，本文均建立低阶的GARCH族模型：GARCH(1,1)、EGARCH(1,1)、APARCH(1,1)、TGARCH(1,1)和CGARCH(1,1)。文献[15]介绍了本文所用GARCH模型的理论基础和模型需满足的条件。

本文针对日前电价的波动特征，对残差做了正态分布和学生t分布的假设来对GAECH族模型进行估计。学生t分布是一种离散程度比正态分布高的随机分布，其密度函数如式(4)表示。

通过对残差做正态分布和学生t分布的假设来估计GARCH族模型的系数，并比较不同假设下GARCH族模型的预测精度。

3 实证结果分析

3.1 均值方程与条件异方差方程参数估计结果

表2是均值方程(2)~方程(4)的系数估计结果。由表2可知，均值方程中各系数均在1%的水平下显著不为零，自回归项系数之和从0.697到0.981，均小于1。对于ARMA模型来说其稳定的条件是自回归项系数之和小于1，表明该模型稳定。

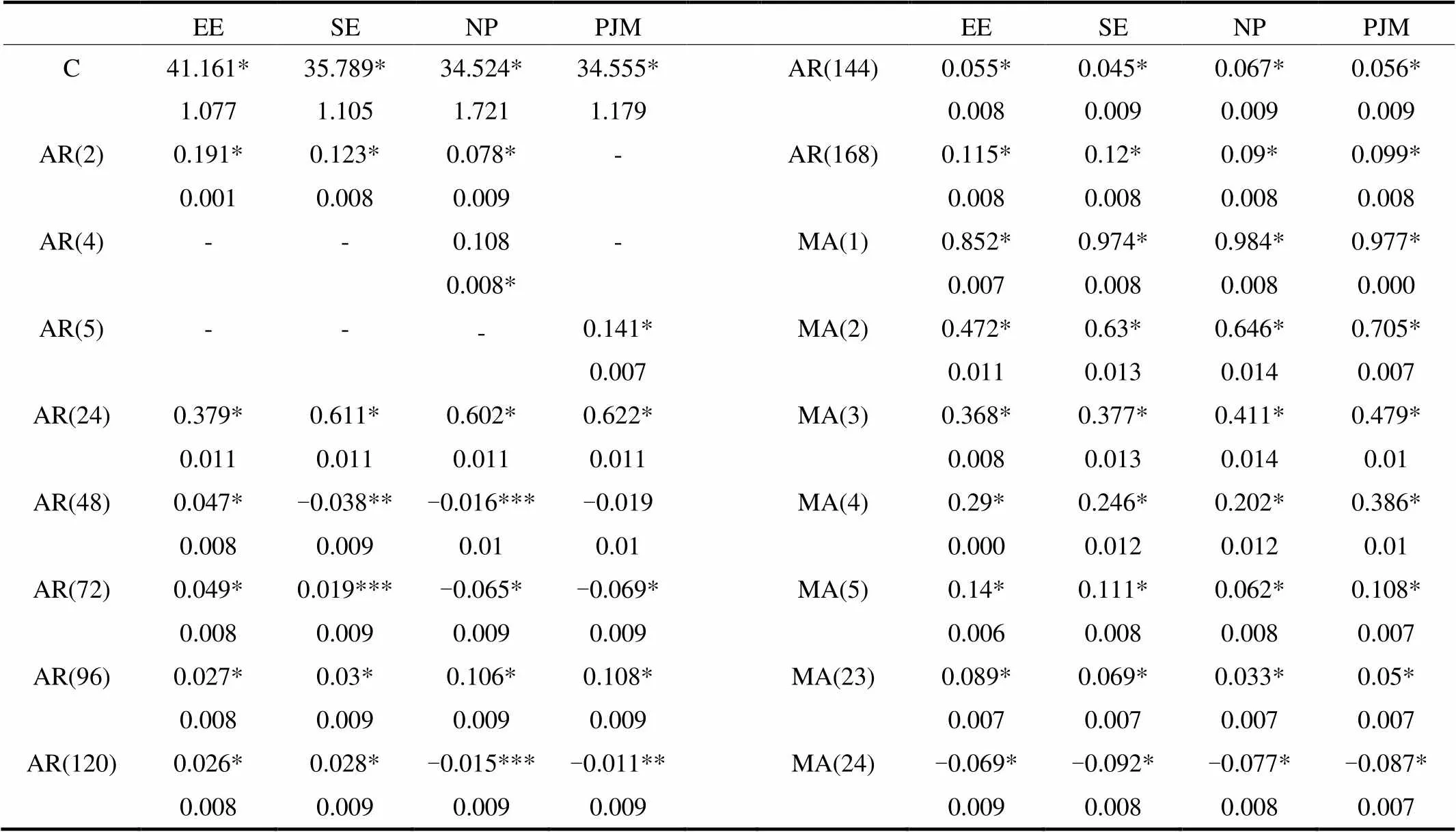
表 2 均值方程系数估计结果

注：该表给出了各个参数的估计值及其标准误，*、**、***分别表示1%、5%和10%的显著水平。

在Eviews7.0中使用GARCH- LM检验对ARMA模型中的残差做ARCH效应检验，结果表明四组市场数据的残差均存在ARCH效应，故建立条件异方差模型来拟合电价数据特征。表3是残差服从正态分布和学生t分布的条件异方差模型的估计结果。由表3可以得到GARCH族模型中各系数的估计结果及相应的标准误。

① 表3中A部分是GARCH(1，1)的参数估计结果。在EE节点处残差服从学生t分布时，模型GARCH(1，1)-t的常数项和异方差项不显著，表明GARCH(1，1)-t不适合EE节点处的电价数据。其他的模型对四组数据拟合的系数和的和小于1，即模型稳定。

② 表3中B部分是TGARCH(1，1)的参数估计结果。对于四组数据来说，残差服从正态分布和学生t分布时，模型的和的和都小于1，表明模型稳定。并且非对称项小于0，表明负杠杆效应存在。

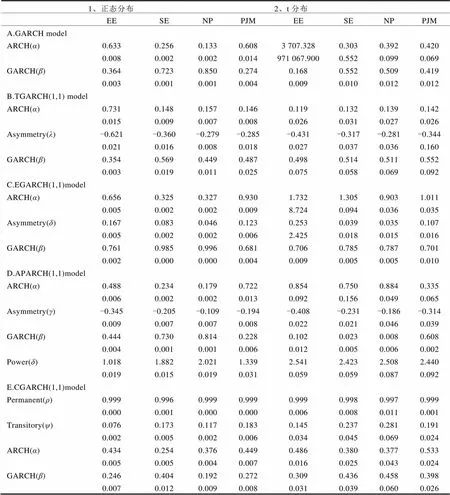
表3 条件异方差系数估计

注：表给出了模型的系数估计值以及相应的标准误。

③ 表3中C部分是EGARCH(1，1)的估计结果。当残差服从正态分布和学生t分布时，模型的非对称项均大于0，并且其估计值在1%的水平下都是显著的，结果同样验证了电价序列的负杠杆效应。

④ 表3中D部分是APARCH(1，1)的参数估计结果。当残差服从正态分布和学生t分布时，为负，在1%的水平下显著不为0。APARCH(1，1)中的幂参数显著的不为1，表明建立这样的非线性模型是适当的。

⑤ 表3中E部分是CGARCH(1，1)的参数估计结果。在假设四组电价数据正态分布和学生t分布时，参数取值从0.996到0.999，表明长期的扰动对条件方差影响是持续存在的。并且CGARCH(1，1)-N中比GARCH(1，1)-N中小，CGARCH(1，1)-t中的比GARCH(1，1)-t中的小，表明短期的波动的影响较弱。

3.2 预测结果

对电价序列建立ARMA-GARCH族模型之后，需要对ARMA-GARCH族模型的预测效果进行检测。Eviews7.0中模型的预测精度从均方根误差(RMSE)、平均绝对误差(MAE)、平均绝对百分误差(MAPE)和希尔不等系数(TIC)四个指标值的大小来反应，数值越小表明模型的预测误差越小精度越高。表4是各个模型在不同残差分布假设下的预测结果。通过比较表示4中RMSE、MAE、MAPE和TIC值的大小，可以比较不同模型对同一组数据的预测效果。

① GARCH族模型在EE节点处的预测精度比较

由表4可知，在不同的分布假设下，EE节点处EGARCH(1，1)的预测效果都不佳。在残差服从正态分布时，APARCH(1，1)-N模型具有较小的RMSE和TIC值，CGARCH(1，1)-N具有较小的MAE和MAPE值。在残差服从学生t分布时，GARCH(1，1)-t具有较小的MAP值，TGARCH(1，1)-t具有较小的RMSE和TIC值，APARCH(1，1)-t的MAE值最小。综上可知，在正态分布和学生t分布的假设下， EGARCH(1，1)模型预测效果最差。

② GARCH族模型在SE节点处的预测精度比较

由表4可知，在SE节点处EGARCH(1，1)-t预测效果最好。在对残差分布假设服从正态分布和学生t分布时，EGARCH(1，1)都表现出了最高的预测精度，RMSE、MAE、MAPE和TIC值较其他四个模型小，即 EGARCH(1，1)对SE节点处的电价数据拟合较好，并具有较高的预测精度。EGARCH (1，1)-t模型的RMSE、MAE和MAPE值比EGARCH (1，1)-N模型的值小， EGARCH(1，1)-t的TIC值较大。由此可以认为，EGARCH(1，1)-t模型预测效果最好。

表4 预测结果

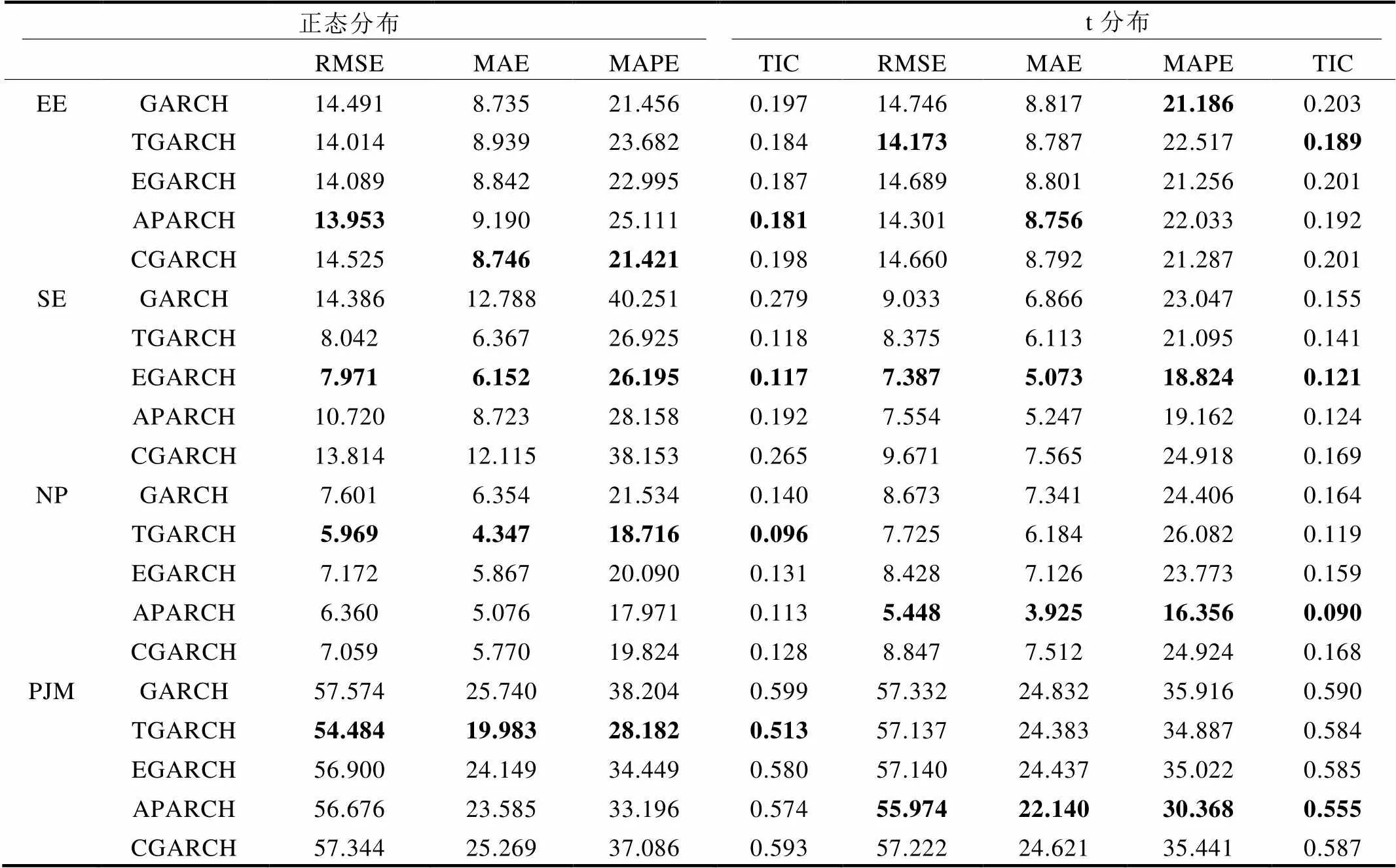
Table 4 Out-of-sample forecasting results

注:黑色字体标注的为同一电力市场中RMSE、MAE、MAPE和TIC的最小值。

③ GARCH族模型在NP市场中的预测精度比较

由表4可知，APARCH(1，1)-t对北欧电力市场系统电价具有较高的预测精度。当残差服从正态分布时，TGARCH(1，1)-N的RMSE、MAE、MAPE和TIC的值都最小。在残差服从学生t分布时，APARCH(1，1)-t具有最高的预测精度，RMSE、MAE、MAPE和TIC的值较其他四个模型的相应值都小。APARCH(1，1)-t的四个指标值均小于TGARCH(1，1)-N的相应值，故APARCH(1，1)-t对北欧电力市场系统电价具有较高的预测精度。

④ GARCH族模型在PJM市场中的预测精度比较

由表4可知，TGARCH(1，1)-N对PJM电力市场日前小时电价数据预测效果较好。在残差服从正态分布时，TGARCH(1，1)-N比其他四个模型的预测效果要好，RMSE、MAE、MAPE和TIC的值为最小。同样，在残差服从学生t分布时，APARCH(1，1)-t较其他四个模型具有较高的预测精度，RMSE、MAE、MAPE和TIC的值分别为最小。由于TGARCH(1，1)-N的指标值均小于APARCH(1，1)-t的值，故TGARCH(1，1)-N预测效果最好。

故综上可知，简单的GARCH模型的预测效果较之其他四个模型较差。在对电力市场电价建模时，考虑到电价的负杠杆效应，在模型中加入非对称项的复杂条件异方差模型(TGARCH、EGARCH、APARCH和CGARCH)具有较高的预测精度。

4 GARCH族模型适用性讨论

总的来说，本文所用时间序列模型对以上四组电价数据的拟合效果较好，并具有较高的预测精度。但是，ARMA-GARCH族模型并非适用于所有电力市场，澳大利亚电力市场波动异常剧烈，并且电价序列的相关性较弱，ARMA-GARCH族模型不适用于该电力市场。

澳大利亚(包括新南威尔士、昆士兰州、南澳大利亚、塔斯马尼亚州和维多利亚五个节点)自1990年开始对电力工业进行改革，首先在发电环节进竞争机制，增加市场成员的选择范围。随着改革的进一步推进，澳大利亚电力市场发展日臻完善，且为半个小时竞价一次，故电价数据为半小时数据。

本文所用数据为五个节点2013年1月1日到2014年11月1日的半小时电价，共32 112个数据。

因为澳大利亚电力市场受负荷、天气等的影响，导致电价波动率异常剧烈。以下选取昆士兰州电价为例进行说明。图1为昆士兰州电价的时间序列图，由图1可知电价序列的极值跳跃很明显，最大值高出最小值6 000多个单位，偏度和峰度值较大，并且存在负的电价值。综上可得，澳大利亚电力市场的价格尖峰更为明显，波动更剧烈。

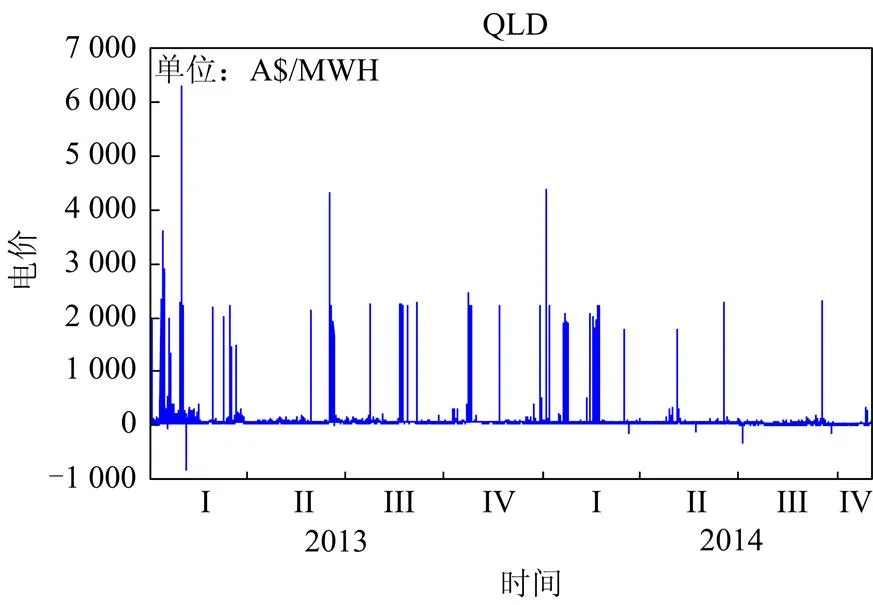
图1昆士兰州电价时间序列图

Fig. 1Graph of electricity price of Queensland

对澳大利亚电力市场各节点数据进行单位根检验可知，电价序列均稳定。检验电价序列的自相关和偏自相关函数值时，Eviews7.0的结果显示，五个节点的电价序列的自相关和偏自相关函数值都比较小，即说明电价序列的相关性不显著。ARMA- GARCH族模型拟合优度甚至达不到10%。即ARMA-GARCH族模型并不适用于澳大利亚电力市场。

由上可知，对于波动率异常剧烈，受外部因素影响较大，且电价序列相邻时段的相关性较弱的电力市场来说，简单ARMA-GARCH族模型拟合优度较低，适用性较差。

5 结论

在解除管制的电力市场中，日前电价的预测对市场参与者来说至关重要。对电价的精准预测可以给发电商提供调整供给的必要信息使其获得最大的利益。与此同时，也可以使消费者调整自己的购电计划，以最小的成本获得最大收益。随着市场管制的进一步放松，对市场电价的建模以及对电价的预测变得更为重要。

本文用北欧电力市场和美国PJM电力市场的电价数据，针对电价序列的价格尖峰条件异方差性等特征，建立了ARMA-GARCH族(GARCH、TGARCH、EGARCH、APARCH和CGARCH)模型，对残差做了正态分布以及学生t分布的假设来拟合电价序列的“尖峰”“厚尾”。并用MSE、MAE、MAPE和TIC四个指标来检验以上模型的预测精度。

对本文所选用的不同数据，GARCH族模型的预测精度不同，总的来说包括门限项和非对称项的条件异方差模型(TGARCH、EGARCH、APARCH和CGARCH)表现预测效果较好，由此验证了电价序列存在负杠杆效应等特征。

但是，ARMA-GARCH族模型并不适用于所有电力市场，例如澳大利亚电力市场电价波动剧烈，电价序列之间的相关性较弱，针对该类电价序列要分析数据特征之后，选择合适的模型进行电价预测，提高预测精度。

[1] MOHAMMAD S, HATIM Y, LI Zuyi. Market operations in electric power systems[M]. New York: Wiley, 2002: 1-30.

[2] GONZALEZ A M, ROQUE A M S, GARCIA- GONZALEZ J. Modeling and forecasting electricity prices with input/output hidden Markov models[J]. IEEE Transactions on Power Systems, 2005, 20(1): 13-24.

[3] 陈思杰, 周浩. 电力市场电价预测方法综述[J]. 继电器, 2006, 34(11): 54-60.

CHEN Sijie, ZHOU Hao. Electricity price forecast method of electricity market[J]. Relay, 2006, 34(11): 54-60.

[4] 黄建柏, 周赛美, 邵留国. 电价预测模型发展及综述[J]. 电力系统保护与控制, 2008, 36(19): 81-84.

HUANG Jianbo, ZHOU Saimei, SHAO Liuguo. Review and development of power price forecasting models[J]. Power System Protection and Control, 2008, 36(19): 81-84.

[5] 张显, 王锡凡. 短期电价预测综述[J]. 电力系统自动化, 2006, 30(3): 92-101.

ZHANG Xian, WANG Xifan. Review of electricity price forecasting[J]. Automation of Electric Power Systems, 2006, 30(3): 92-101.

[6] 徐永丰, 吴洁晶, 黄海涛, 等. 考虑负荷率的谷峰分时电价模型[J]. 电力系统保护与控制, 2015, 43(23): 96-103.

XU Yongfeng, WU Jiejing, HUANG Haitao, et al. Time-of-use tariff model considering load factor[J]. Power System Protection and Control, 2015, 43(23): 96-103.

[7] 文旭, 郭琳，王俊梅. 面向节能减排的电力系统发购电计划研究述评[J]. 电力系统保护与控制, 2015, 43(8): 136-144.

WEN Xu, GUO Lin, WANG Junmei. Overview of power dispatch and purchasing plan in power system from energy-saving and emission-reducing[J]. Power System Protection and Control, 2015, 43(8): 136-144.

[8] ATILLA C. Forecasting electricity price volatility with the Markov-switching GARCH model: evidence from the Nordic electric power market[J]. Electric Power System Research, 2013, 102: 61-67.

[9] ENGLE R F. Autoregressive conditional heter-oscedasticitywith estimates of variance of United Kingdom inflation[J]. Econometric, 1982, 50(4): 987-1007.

[10]王瑞庆, 王宏福. 基于t分布GARCH模型的电价波动时变性研究[J]. 电力系统保护与控制, 2011, 39(23): 49-53.

WANG Ruiqing, WANG Hongfu. Investigation on time- volatility of electricity price based on GARCH model with student-t[J]. Power System Protection and Control, 2011, 39(23): 49-53.

[11] SOLIBAKKE P B. Efficiently estimated mean and volatility characteristics for the Nordic spot electric power[J]. Market International Journal of Business, 2002, 7(2): 1083-4346.

[12] LIU Heping, SHI Jing. Applying ARMA — GARCH approaches to forecasting short-term electricity prices[J]. Energy Economics, 2013, 37: 152-166.

[13] BOWDEN N, PAYNE J E. Short term forecasting of electricity prices for MISO hubs: evidence from ARIMA-EGARCH models[J]. Energy Economics, 2008, 30: 3186-3197.

[14]熊尚飞, 邹小燕. 电力市场价格风险价值与波动预测研究综述[J]. 电力系统保护与控制, 2014, 42(2): 146-153.

XIONG Shangfei, ZOU Xiaoyan. Value at risk and price volatility forecasting in electricity market: a literature review[J]. Power System Protection and Control, 2014, 42(2): 146-153.

[15] HICKEY E, LOOMIS D, MOHMMADI H. Forecasting hourly electricity prices using ARMAX — GARCH models:an application to MISO hubs[J]. Energy Economics, 2012, 34(1): 307-315.

(编辑 葛艳娜)

Comparison of GARCH models in electricity price forecasting

LIU Liyan, ZOU Xiaoyan

(School of Economics and Management, Chongqing Normal University, Chongqing 401331, China)

Electricity price fluctuates wildly which makes huge risk. Accurately predicting the electricity price will contribute to market participants to manage risk and maximize the profit of participants. This paper applies ARMA—GARCH models to forecast day-ahead electricity prices in PJM electricity market and Nord Pool. With the assumption that residuals obey normal and student’s t distributions, this paper compares the prediction accuracy of different ARMA-GARCH models, and finds that in most cases the asymmetric GARCH models perform well. But the ARMA-GARCH models can not be applied in the electricity market in which price volatility is extremely huge and the correlation between electricity price serials is weak, such as Australia electricity market.

This work is supported by National Natural Science Foundation of China (No. 71201180).

electricity market; electricity forecasting; GARCH models

10.7667/PSPC150775

国家自然科学基金(71201180)；教育部人文社会科学研究项目(10XJC79006)

2015-05-10；

2015-08-22

刘丽燕(1989-)，女，硕士研究生，主要研究方向为电力市场电价预测；E-mail:zrxlunwen1@163.com

邹小燕(1979-)，女，博士，教授，主要研究方向为电力市场竞价机制设计，风险管理。