无粘结预应力简支试验梁变形和应力分析

张冬久

(中铁第五勘察设计院集团有限公司东北分院，黑龙江 哈尔滨　150006))



无粘结预应力简支试验梁变形和应力分析

张冬久

(中铁第五勘察设计院集团有限公司东北分院，黑龙江 哈尔滨150006))

摘要：无粘结预应力技术在工程中的应用越来越广泛，对无粘结预应力结构的研究也越来越重要。以1片试验梁为研究对象，通过分级施加竖向荷载和预加力，测试各级荷载作用下试验梁的变形和应力(应变)，采用ANSYS有限元软件建立试验梁的有限元分析模型，

关键词：无粘结预应力；简支梁；试验；变形；应力

1试验设计

1.1试验梁设计

试验梁截面尺寸为200 mm×200 mm，梁总长为3 100 mm，计算跨径为3 000 mm，预应力筋采用1束7Φs15.2 mm的1 860级钢绞线，公称截面面积为139 mm2，锚垫板采用200 mm×200 mm×10 mm的Q235钢板，底部和顶部主筋分别采用2根直径为12 mm的HRB335钢筋，箍筋采用直径为8 mm的R235钢筋，设计混凝土标号为C30，试验梁预留管道在预应力筋张拉后不灌浆，确保预应力筋处于无粘结状态，纵向预应力筋为通过截面形心的直线预应力筋。

1.2加载方案

(1)竖向荷载

对试验梁进行静力试验，对混凝土应变、钢筋应变和变形进行测试。试验梁在竖向荷载作用下不仅会产生弯矩，而且会产生剪力，为减少剪力的影响，采用两点对称加载的方式，本试验重点研究剪力为零的“纯弯段”内梁的正截面受力状态和变形规律。扣除结构自重所产生的变形和应变，分析试验梁在各加载阶段的变形和应变情况。施加集中荷载模拟梁的不同恒载作用，同时要控制竖向集中荷载的大小，保证试验梁在试验过程中不产生裂缝、不失稳，竖向荷载位置，其中L表示试验梁的计算跨径，F表示竖向恒载，采用三级加载，每级递增2 kN，分别为2 kN、4 kN、6 kN。可以看出，试验加载距离两侧支点各L/3，中间的L/3为理论“纯弯段”。

由于混凝土梁中的微小裂缝会对梁的静力参数产生很明显的影响，因此明确多大的预加力将使梁中产生拉应力及裂缝至关重要。同时，在确保预加力不使预应力混凝土简支梁失稳及受压区混凝土破碎的情况下，计算张拉预加力时的最大值，通过计算可以得出试验梁最大预加力为123.5 kN，在试验过程中，预加力采用120 kN作为最大值。

预应力筋从0 kN开始，分级张拉，在每级预加力作用下再分级施加竖向荷载。竖向荷载加载到预定级别时卸载，再张拉下一级预加力。每两级竖向加载之间的时间间隔不少于10 min，每两级预加力之间时间间隔不少于45 min。

2有限元模型

2.1无粘结预应力模拟

在预应力混凝土梁中对无粘结的预应力的模拟通常有下面的两种方法：等效荷载法和实体力筋法。等效荷载法最突出的特点是模型的建立简便，预应力钢筋的布置形式不予以考虑，网格划分简洁、便利，程序比较容易收敛，且可以直观的表现出预应力工作时预应力梁的整体响应效果，大部分运用于杆系结构的研究；等效荷载法最明显的缺点就是预应力筋在混凝土梁内部布置时不能对预应力的分布和方向进行模拟。实体力筋法模拟预应力混凝土梁最常用的方法有初始应变法和降温法。初始应变法通常不能考虑预应力损失，每个单元的实常数各不相等，工作量很大。降温法是给预应力筋单元施加温度值来模拟预应力值，温度值可以利用张拉预应力值来反算，降温法来模拟张拉预应力简单易行，在外力共同作用时，也可考虑外力与预应力的共同作用，同时也能模拟外力作用对预应力筋的影响。

通过比较两种方法的优缺点，结合试验梁的实际情况，本论文无粘结预应力试验梁采用实体力筋法中的降温法来模拟预应力变化。温度改变值按下式计算

式中：σ为预应力钢筋的张拉应力；E为预应力钢筋自身的弹性模量；α为预应力钢筋自身的线膨胀系数。

2.2有限元模型建立

试验梁有限元模型采用ANSYS软件建立，混凝土采用SOLID65模拟，钢筋及预应力筋采用LINK8模拟。

3结果分析

3.1变形分析

图1和图2反映出试验梁在竖向荷载作用下产生向下的变形，变形形状呈现为抛物线形。

实测、有限元计算、公式计算的试验梁在不同预加力情况下变形随预加力的变化数值见表1，变化情况如图4所示。

图1　变形—预加力曲线图

从表1和图3中可以看出：在各级竖向荷载作用下，公式计算变形值最大，有限元计算变形值次之，实测变形值最小，进而得出采用公式计算变形偏于保守，进行结构设计是偏于安全的；在同级竖向荷载作用下，预加力的增加会导致试验梁的变形值减小，这是因为预加力增加使截面的刚度增大，变形随预加力增加减小幅度不大；在同一级预加力作用下，变形随竖向荷载的增大而增大，例如当预加力为90 kN时，2 kN、4 kN、6 kN竖向荷载作用下，实测变形值分别0.225 mm、0.460 mm、0.715 mm，

3.2应力(应变)分析

在竖向荷载作用下试验梁的应变情况示意图，如图2～图3所示。

图5反映出在竖向荷载作用下，试验梁跨中截面下缘承受拉应力，上缘承受压应力。从图6中可以看出试验梁左右支点各L/3范围，上缘钢筋和下缘钢筋的应力分布图呈现为对称的三角形，中间段L/3范围应力分布图呈现为对称的矩形，也就是“纯弯段”，在整个跨径L范围应力呈现为低腰梯形，其中上缘钢筋为压应力，下缘钢筋为拉应力。

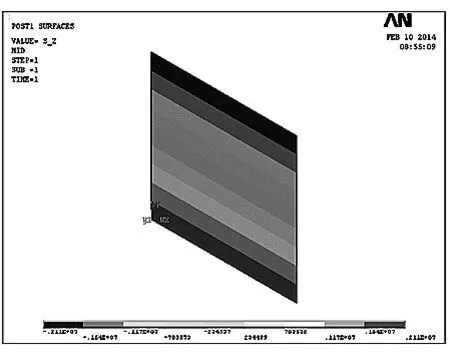
图2　试验梁跨中应变示意图

图3　试验梁纵向钢筋应变示意图

试验梁在不同预加力情况下应变随预加力值的变化曲线示意图，如图4～图7所示，图中负值表示压应变，正值表示拉应变。

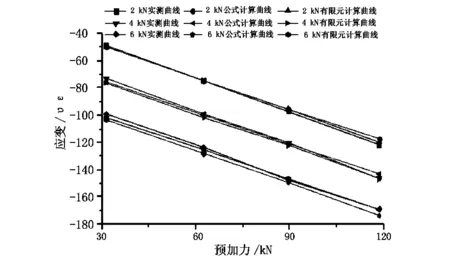
图4　试验梁顶面混凝土应变—预加力曲线图

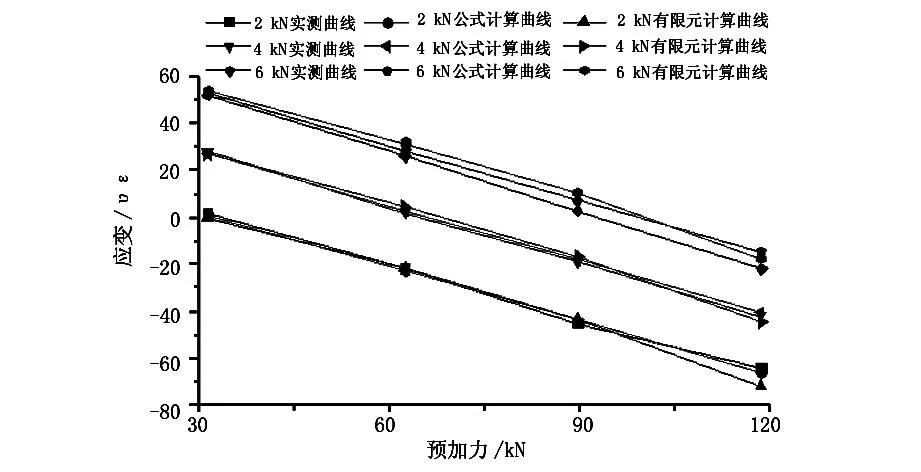
图5　试验梁底面混凝土应变—预加力曲线图

从图2和图3中可以看出：在各级竖向荷载作用下，试验梁顶面和底面混凝土实测应变值、公式计算应变值与有限元计算应变值相差很小，三者相符；在同级竖向荷载作用下，随着预加力的增加，试验梁顶面混凝土的压应变不断增大，表现为线性变化，试验梁底面混凝土的应变由拉应变转变为压应变，变化趋势也表现为线性，例如当竖向荷载为4 kN时，预应力从30 kN增大到120 kN的过程中，顶面混凝土应变由-73 με变化到-145 με，底面混凝土应变由28 με变化到-39 με；在同级预加力作用下，随着竖向荷载的增大，混凝土顶面和底面的应变值也不断的增大。

图6　试验梁顶面钢筋应变—预加力曲线图

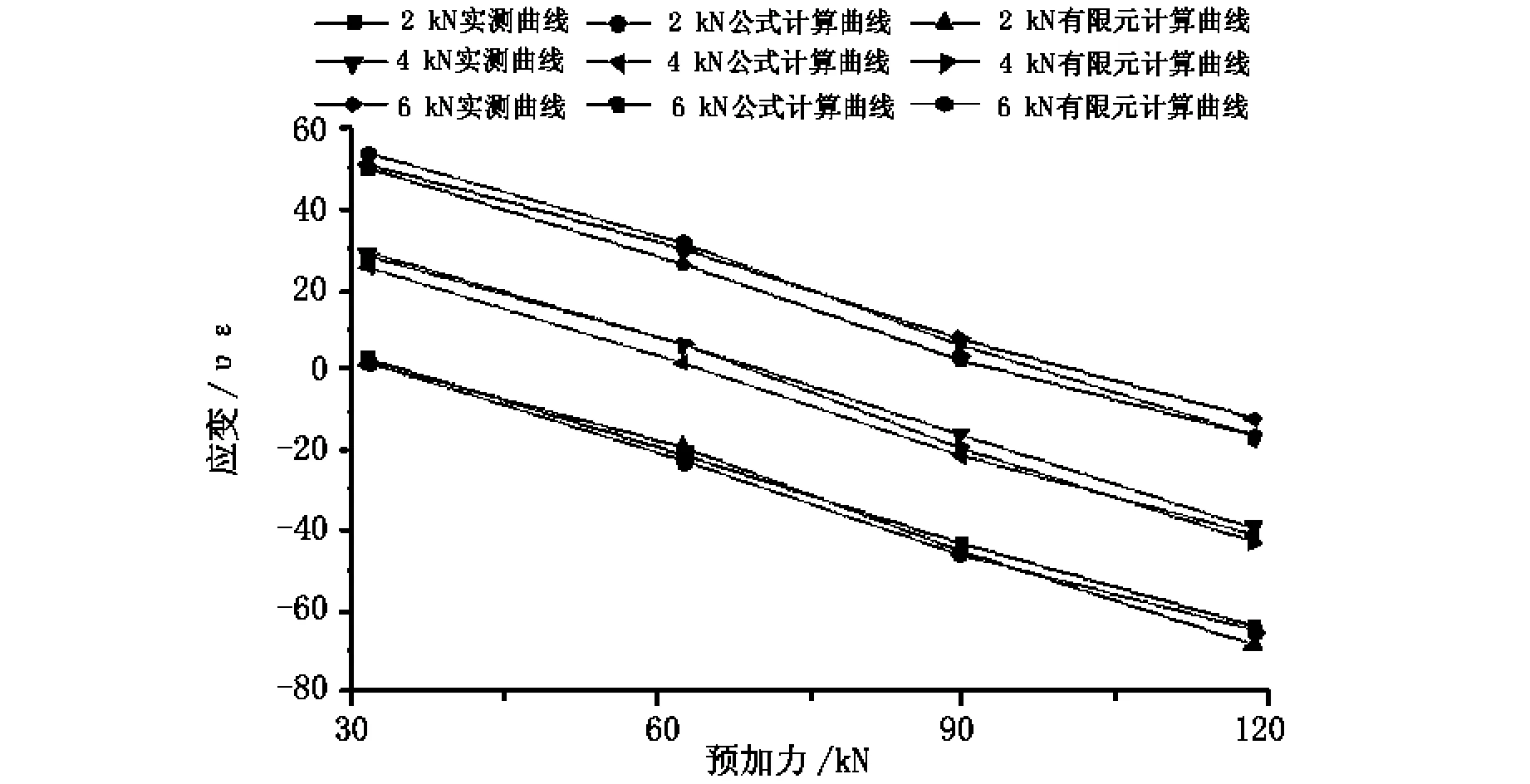
图7　试验梁底面钢筋应变—预加力曲线图

从图3和图4中可以看出：在各级竖向荷载作用下，试验梁顶面钢筋和底面钢筋实测应变值、公式计算应变值与有限元计算应变值相差很小，三者相符；在同级竖向荷载作用下，随着预加力的增加，试验梁顶面钢筋的压应变不断增大，表现为线性变化，试验梁底面钢筋的应变由拉应变转变为压应变，变化趋势也表现为线性，例如当竖向荷载为8 kN时，预应力从30 kN增大到120 kN的过程中，顶面钢筋应变由-50 με左右变化到-115 με左右，底面钢筋应变由50 με左右变化到-10 με左右；在同级预加力作用下，随着竖向荷载的增大，混凝土顶面和底面的应变值也不断的增大。

4结论

(1)在各级荷载作用下，试验梁的试验实测值、有限元计算值和理论公式计算值三者相符。

(2)各级竖向荷载作用下，预加力的增加会导致试验梁的变形和应力(应变)减小，表明预加力会使试验梁刚度增加。

参考文献：

[1]谢功元. 在役混凝土梁永存预应力试验研究[D].长安大学,2004.

[2]贾艳敏,王佳伟,韩基刚. 预应力简支钢箱梁固有频率影响因素分析[J].工程力学,2009，(S1):37-40.

[3]张冬久,孙全胜. 预应力对PC梁动静刚度影响的试验研究[J].低温建筑技术,2013,(7):72-75.

收稿日期：2016-01-12

作者简介：张冬久(1987-)，男，吉林九台人，硕士，从事建筑结构设计与研究。

中图分类号：U442

文献标识码：C

文章编号：1008-3383(2016)05-0097-02