变力做功问题探讨

赵才松

(阳新县狄田中学，湖北　黄石　435239)



变力做功问题探讨

赵才松

(阳新县狄田中学，湖北黄石435239)

摘要：应用积分的基础思想,采用“分割、近似求和、取极限”的方法探讨变力做功的问题。结合高等数学中定积分的计算公式,分析了变力做功的计算方法。

关键词：变力做功;极限;积分

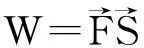
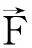
然而,在现实生活中,力的大小和方向在做功的过程中常常会发生变化,这就是变力做功问题。例如:

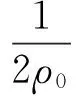
这是比较典型的变力做功的例子,这种情况下很难套用前面提到的公式。事实上,变力做功问题是人们一直关心和研究的物理问题之一[3]。本文将应用定积分的基本思想,采用“分割、近似求和、取极限”的方法探讨变力做功的问题,然后结合高等数学中定积分的计算公式,分析了变力做功的计算方法。

一、 变力做功问题分析

本节以一般的例子,通过数学中极限逼近[3]的思想,采用“分割、近似求和、取极限”的方法来分析变力做功的问题。基本思想是在运动的极小段位移内,用“恒力”代替变力做功。

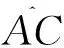
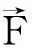
从而力沿曲线所做的功

(2.1)

(2.2)

二、 变力做功问题的计算

∫LP(x,y)dx+Q(x,y)dy.

(3.1)

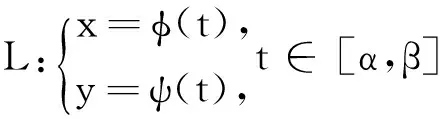
其中φ(t),ψ(t)在[α,β]上具有一阶连续导函数,点A与点B坐标分别为(φ(α),ψ(α))和(φ(β),ψ(β))。设P(x,y)与Q(x，y)为L上的连续函数,则(3.1)式中沿L从点A到B的积分有如下计算公式[5]

∫LP(x,y)dx+Q(x,y)dy=∫αβ[P(φ(t),ψ(t))φ'(t)+Q(φ(t),ψ(t))ψ'(t)]dt

(3.2)

从以上分析可以看出,在变力做功的计算问题中有两个因素非常关键,一是力的大小和方向的描述,二是力的位移(所经过的有向曲线段)的描述。下面用具体的例子来说明变力做功的计算问题。

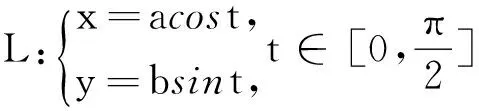
W=∫Lkxdx+kydx

对于三维空间中变力做功的问题,我们一样可以用第二节的方法,采用“分割、近似求和、取极限”的方法来分析变力所做的功。

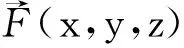
=(P(x,y,z),Q(x,y,z),R(x,y,z)),沿空间曲线

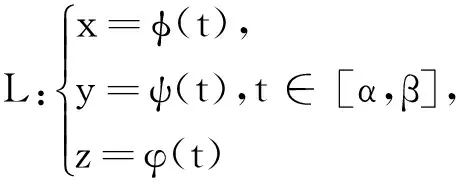
从点A(φ(α),ψ(α),φ(α))运动到点B(φ(β),ψ(β)，φ(β))与公式(3.2)类似,在这个过程中该力所做的功为

W=∫LP(x,y,z)dx+Q(x,y,z)dy+R(x,y,z)dz

=∫αβ[P(φ(t),ψ(t),φ(t))φ'(t)

+Q(φ(t),ψ(t),φ(t))ψ'(t)+R(φ(t),ψ(t),φ(t))φ'(t)]dt

例2 设一质点受力作用,力的方向指向原点,大小与质点到xy平面的距离成反比。若质点沿直线x=at,y=bt,z=ct(c≠0)从M(a,b,c)移动到N(2a,2b,2c),求力所做的功。

解：设比例系数为k,则力可表示为

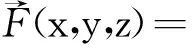
),力移动所经过的曲线参数方程为,故力所做的功为

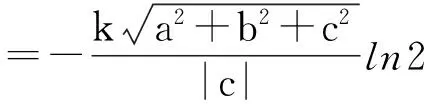
三、结语

本文采用“分割、近似求和、取极限”的方法探讨变力做功的问题,然后结合高等数学中定积分的计算公式,分析了变力做功的计算方法。运用数学中极限逼近的思想,在运动的极小段位移内,用“恒力”代替变力计算它所做的功,然后把每一小段位移上所做的功进行累加,得到整个过程中变力所做的功。

参考文献：

[1]人民教育出版社等.义务教育教科书《物理》(八年级,下册)[M].北京：人民教育出版社,2012.

[2] 人民教育出版社等.普通高中课程标准实验教科书《物理》(2)[M].北京：人民教育出版社,2010.

[3] 陈曙光，许迈昌.大学物理学[M].长沙：湖南大学出版社,2013.

[4] 华东师范大学数学系.数学分析(第4版上册)[M].北京：高等教育出版社,2010.

[5] 华东师范大学数学系.数学分析(第4版下册)[M].北京：高等教育出版社,2010.

文章编号：2095-4654(2016)04-0020-02

收稿日期：2016-01-18

中图分类号：O175.2

文献标识码：A