车辆荷载作用下钢波纹板拱桥应变分析

方诗圣,黄志福,邹祥强,孟再生

(1.合肥工业大学 土木与水利工程学院,安徽 合肥　230009;2.安徽省交通控股集团有限公司,安徽 合肥　230088)



车辆荷载作用下钢波纹板拱桥应变分析

方诗圣1,黄志福2,邹祥强1,孟再生1

(1.合肥工业大学 土木与水利工程学院,安徽 合肥230009;2.安徽省交通控股集团有限公司,安徽 合肥230088)

摘要:文章依托安徽泗洪至许昌高速公路淮北段钢波纹板拱桥工程实例,采用ANSYS软件建立该桥的等效实体模型,对钢波纹板拱桥在车辆荷载作用下的应变进行模拟计算,将计算结果与现场实测数据进行对比分析,验证了所建模型的有效性和可行性。在该模型基础上研究公路-Ⅰ级车辆动荷载下的应变变化规律。研究结果表明:在车辆荷载作用下,边跨各位置整体受到拉应变,且拱脚处的应变值稍大于其他位置;车速的改变并不改变钢波纹板拱桥各测点位置的应变规律,而钢波纹板拱桥各测点的应变值与车速大小成正比。

关键词:钢波纹板;拱桥;车辆荷载;有限元;应变分析

0引言

钢波纹板拱桥是一种新型的桥涵结构形式,它主要以钢波纹板和土体作为建筑材料形成覆土钢波纹板拱桥结构,土和结构的相互作用极大地提高了结构的自身承载力[1]。钢波纹板结构作为一种典型的地下柔性结构,相对于普通的钢筋混凝土和圬工结构,具有对地基要求相对低、雨季施工速度快、不需要养生及不受气温影响等特点,对软土、膨胀土地区地基不均匀沉降有优良的适应性,而且波纹钢造价低、可回收利用率高,克服了钢筋砼材料回收难题等优势,因此具有很好的推广价值和应用前景[2]。在我国,这种结构的应用和研究才刚刚起步,目前的有限元计算模型主要有三维空间模型和平面应变模型[3-4]。三维空间模型考虑了结构与土体共同的节点位移,而平面应变模型则考虑的是土体本构和接触的影响[5]。

国内仅对钢波纹板桥涵的土压力、受力与变形变化规律及施工因素等对结构的影响进行了单一的研究[6-9],而将数值分析与现场试验结果对比的并不多见。本文将有限元数值分析与现场试验结果进行对比分析,验证了该模型的有效性和可行性,在该基础上对钢波纹板拱桥在车辆动荷载下的受力性能进行分析。

1有限元模型的建立

泗洪至许昌高速公路(泗许高速)淮北段百善互通匝道FK0+517处小桥上部采用3孔的钢波纹板拱桥,每孔跨径均为4 m、路基宽度为12 m,钢波纹板波形为150 mm×50 mm×28 mm,壁厚为5 mm,管顶覆土高度为1.2 m,路面结构为36 cm水泥稳定碎石基层+18 cm沥青混凝土面层。下部墩台均采用钢筋混凝土现浇完成。

本文采用ANSYS软件建立了钢波纹板拱桥结构等效空间模型，如图1所示。

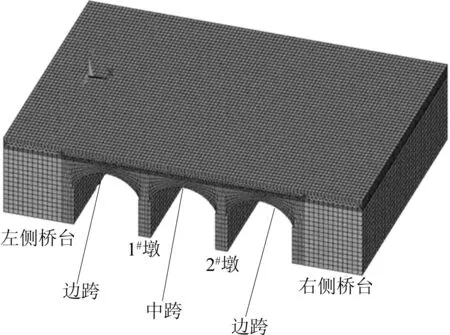
图1　有限元计算模型

具体建模过程如下。

(1)由于钢波纹板特殊的截面性状,在计算分析中单元和节点数目太多，而根据抗弯刚度等效原理把波纹钢板等效简化为平钢板，会在计算上带来较大的便利,其计算结果也可保证一定的准确性[8]，截面等效为平钢板示意图如图2所示。

等效厚度的计算公式为:

(1)

等效密度的计算公式为:

(2)

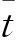
(2)根据文献[9],在结构受外荷载作用下,结构两侧1倍跨径内的土体变形较明显,1倍跨径以外的土体几乎无变化，因此本文取单倍跨径,采用solid45八节点实体单元模拟土体、桥台、桥墩以及路面结构。

(3)为了更好地分析钢波纹板的受力状态,将钢波纹板附近单元加密。土体与波纹钢板接触采用面面接触,采用conta173(conta173表示三维目标面与本单元的柔性面之间的接触和滑移,是三维、四节点低阶四边形单元,可位于三维实体或壳单元(如solid45或shell63)的表面)接触单元来模拟实现。

(4)边界条件。结构底面约束所有位移和扭转自由度施加固定端约束,横桥向侧立面施加顺桥向水平位移约束,顺桥向前后立面施加横桥向水平位移约束。划分后单元总数167 750个,节点总数为154 479个。

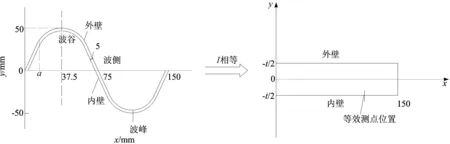
图2　截面等效示意图

2加载工况及计算位置布置

2.1加载工况

对所建钢波纹板拱桥模型进行有限元模拟过程中,所施加的荷载工况与现场试验测试工况加载一致。本文采用的荷载车辆为北奔重卡和欧曼昆仑[10]。北奔重卡装载后总质量为39 t,欧曼昆仑装载后总质量为41 t。本文采用双车顺行(北奔重卡在前,欧曼昆仑在后)对钢波纹板拱桥应变进行测量,测试点位的布设如图3所示，图3的单位均为m。本文荷载的施加位置同样对照现场测试时的布点位置、行驶方向及点位布设。双车顺行时以前车(北奔重卡)后轴中线位于测试点位时为准。

2.2计算位置布置

文献[10-11]的现场测试结果表明:在双车顺行荷载下,波峰、波谷及波侧断面的切向应变虽然数值大小不同,但应变值较为接近,且其变化规律基本一致。由于本文采用等效平钢板模拟钢波纹板,而实际测试时是按照某一断面相邻波形内波峰、波谷和波侧位置(钢波纹板内壁)进行应变测试,文献[10-11]试验结果为本文的计算位置选择提供了方便,因此，本文选择钢波纹板拱桥边跨内壁的拱脚、1/4跨、拱顶和3/4跨作为计算关键位置[10]。将所取节点位置(波峰、波谷或波侧)的数值计算结果与现场实测拱脚、1/4跨、拱顶和3/4跨处实测值进行对比分析。本文只取波峰进行分析,因为波谷和波侧断面实测数据值有微小差异,但都比较接近,且变化规律基本一致。

3数值计算和现场试验结果对比分析

本文依据现场实测的边跨内壁拱顶切向应力以及边跨拱脚、1/4跨、拱顶、3/4跨各位置切向应变随加载位置变化时的实测数据,与同等条件下有限元模拟计算值进行对比分析，结果如图4所示。由图4a可看出,两者随荷载移动的应力变化趋势基本一致,规律相吻合。由图4b可看出,在双车顺行情况下,在荷载位于-8.5～-3.5 m过程中,各测点位置整体产生较小的拉应变，且应变值相差甚微;当荷载位于-3.5～1.5 m时,各位置应变均增大,处于增长期;而自荷载从3.5 m开始到远离拱桥时,各处应变值均浮动较小,保持稳定状态。在同等条件下,有限元模拟值要稍大于现场实测值。

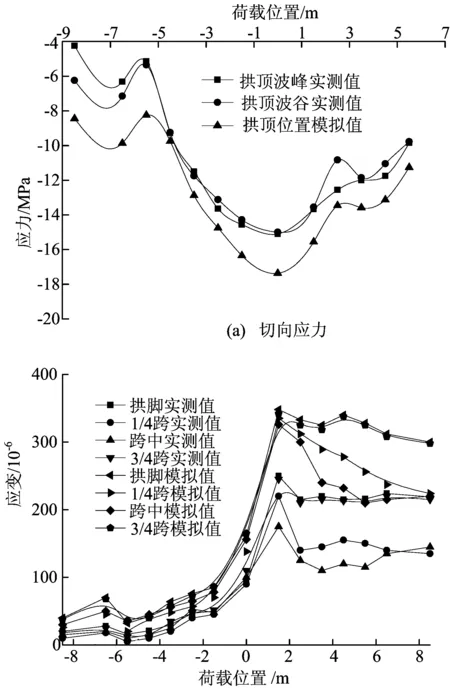
(b)　切向应变

综合以上分析可知,利用有限元软件进行实体建模分析、预测是可行的,其计算结果基本符合现场实际规律。因此本文所建模型是有效可行的,可为进一步车辆动荷载下的应变分析提供理论基础。

4车辆荷载下的应变分析

4.1荷载施加

根据文献[12]施加公路-Ⅰ级荷载。由于钢波纹板拱桥属于填埋式结构,因此活载计算采用车辆荷载[13]。车辆荷载按照时程加载,采用ANSYS软件中的瞬态分析模块,具体加载方法为:

(1)定义加载历程。起始时间为前轮上桥面时刻;终止时间为后轮离开桥面时刻。

(2)选定车辆荷载作用位置和方向。车辆从左往右行驶于车道中间。

(3)设定行车速度为60 km/h,荷载步数目为50步。

(4)根据顺桥向模型长度及车的尺寸计算出总的行车时间和荷载步伐。

(5)根据时间积分分步加载,每步加载前先删除步骤(4)加载的力。

(6)每加载1步,求解1次,最后得到应变包络图。

公路-Ⅰ级荷载计算时以汽车后轴中线位于测试点位时为准。公路-Ⅰ级荷载工况为单车行驶方向为从左往右,计算速度分别为60 km/h和40 km/h。

4.2应变分析

本文通过对所建模型施加车速为60 km/h和40 km/h的动载,研究钢波纹板拱桥在移动车辆动荷载下的应变变化规律。限于篇幅,只给出车速为60 km/h时边跨各位置切向应变随加载位置的变化曲线，如图5所示。

由图5可以看出,在速度为60 km/h公路-Ⅰ级车辆动荷载下,边跨各位置整体受到切应变,最大切应变出现在拱脚,其值为243×10-6,对应的切应力为48.6 MPa,小于钢波纹板Q235钢的屈服强度235 MPa,故在车辆荷载作用下,桥梁安全可靠。

由图5还可以看出，应变在车后轴中心位于-8.5～-3.5 m过程中,各位置切应变均逐渐增大;在-3.5～5.5 m过程中,拉应变整体减小；保持稳定应变值为(40～50)×10-6。在车辆动荷载作用下,钢波纹板拱桥拱脚处的应变值稍大于其他位置处,整体来看,拱脚和3/4跨位置应变较接近,而拱顶和1/4跨位置应变基本相同。

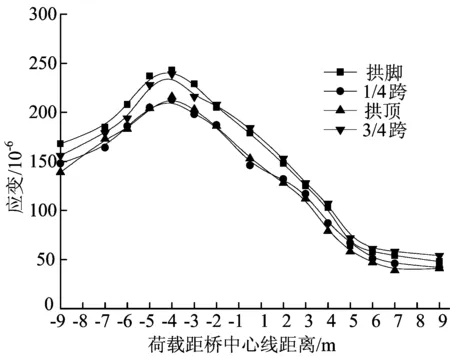
图5　边跨各位置切向应变随加载位置和测试位置的变化

车速分别为40 km/h和60 km/h时,钢波纹板拱桥各位置切向应变对比分析结果如图6所示。

由图6可以看出,车速为60 km/h时各位置的应变均略大于速度为40 km/h时相同位置的应变值,但其变化规律是一致的,速度大小仅对钢波纹板拱桥各位置的应变大小产生影响,并不改变钢波纹板拱桥的应变变化规律。由此可知，钢波纹板拱桥各位置的应变与车辆速度大小成正比。

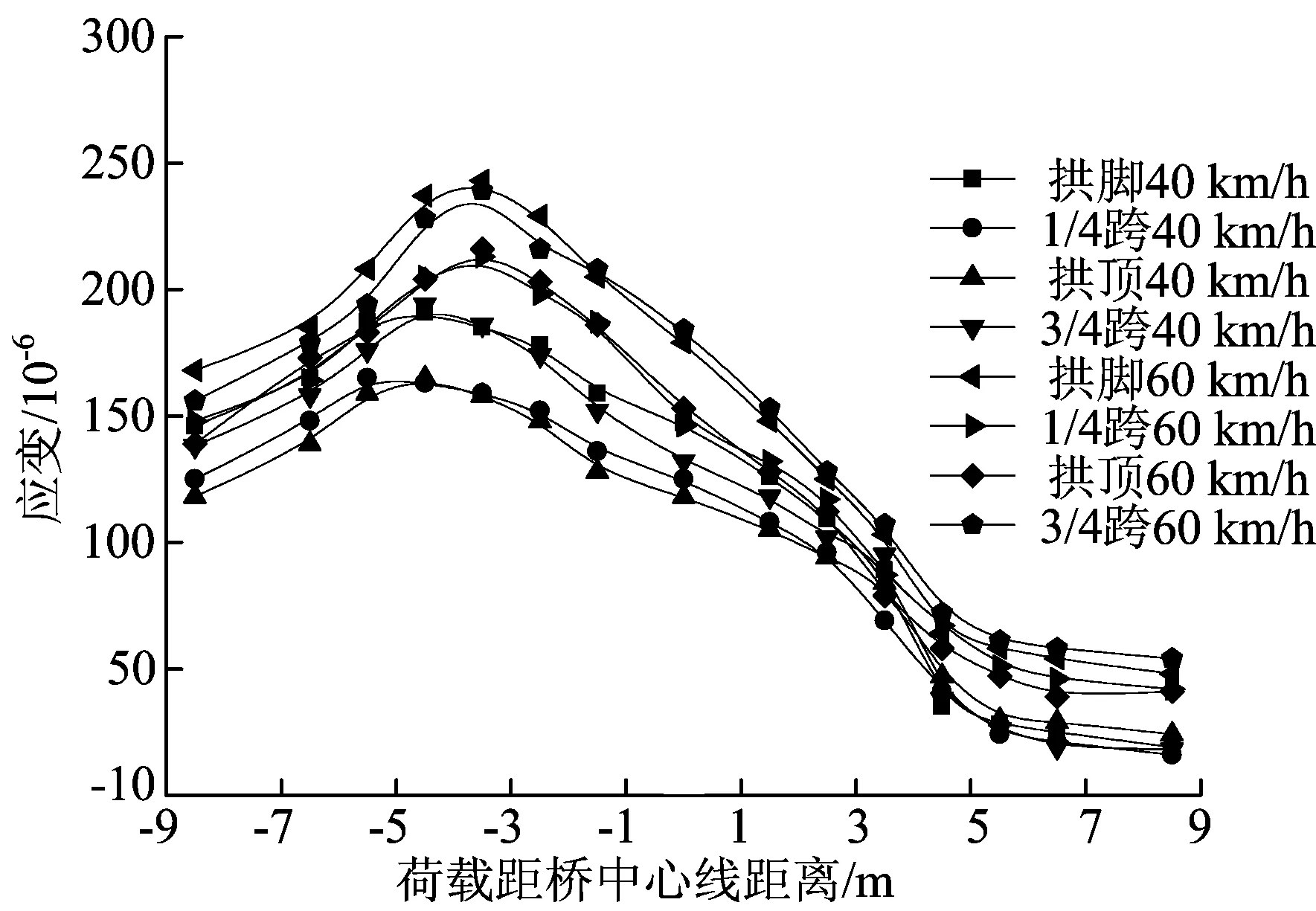
图6　不同车速时边跨各位置的切向应变

车速为60 km/h边跨与中跨各位置的切向应变对比如图7所示,由图7可知,在车辆荷载作用下,中跨与边跨在1/4跨和3/4跨位置处应变变化趋势大致相同,而在拱顶和拱脚位置差异较明显,拱顶处应变中跨比边跨相对于桥跨中心线对称性好,而拱脚处应变中跨比边跨波动性大。从整体来看,中跨各位置处切向应变整体比较均匀。

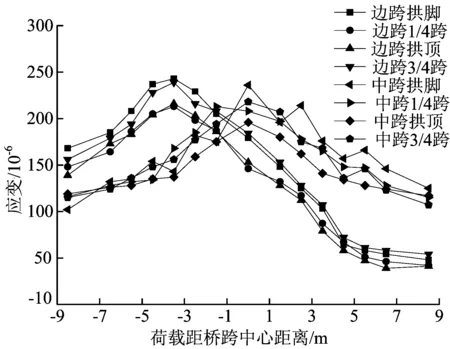
图7　车速为60 km/h边跨与中跨各位置的切向应变对比

5结论

本文应用ANSYS软件建立钢波纹板拱桥的三维实体等效模型,通过加载与现场试验荷载相同的车辆荷载进行静力分析,将静力计算结果与现场实测数据进行对比分析,验证本文所建模型的有效可行性，并在该模型基础上进行车辆荷载动力分析。分析结果表明:

(1)在车辆荷载作用下,边跨各位置整体受拉应变,拱脚和3/4跨位置切应变较接近,而拱顶和1/4跨位置切应变基本相同。最大切应变出现在拱脚,其值为243×10-6,对应的应力为48.6 MPa,小于钢波纹板Q235钢的屈服强度235 MPa,故在车辆荷载作用下,桥梁安全可靠。

(2)在车辆荷载作用下,在车后轴中心位于-8.5～-3.5 m过程中,边跨各位置切应变均逐渐增大,在-3.5～5.5 m过程中,切应变整体减小,此后保持稳定应变值为(40～50)×10-6。

(3)在车辆荷载作用下,钢波纹板拱桥各位置的应变与车速大小成正比，但车速的改变并不会改变其各测点的应变变化规律。

(4)在车辆荷载作用下,中跨与边跨在1/4跨和3/4跨位置处应变变化趋势大致相同,而在拱顶和拱脚位置差异较明显,拱顶处应变中跨比边跨相对于桥跨中心线对称性好,而拱脚处应变中跨比边跨波动性大。从整体来看,中跨各位置处应变整体比较均匀。

[参考文献]

[1]Kang J S,Davidson J S.Structural effects of concrete lining for concrete-lined corrugated steel pipes [J].Structure and Infrastructure Engineering,2013,9(2): 130-140.

[2]冯忠居,乌延玲,贾彦武,等.钢波纹管涵洞受力与变形特性模拟试验研究[J].岩土工程学报,2013,35(1):187-192.

[3]王全录,刘保东,李雨株,等.埋置波纹钢板管涵刚度对其受力性能的影响[J].北京交通大学学报,2012,26(4):1-4.

[4]张孟东.覆土钢板桥涵动力及稳定性分析[D].北京:北京交通大学,2011.

[5]李百建,符锌砂.低拱型波形钢板桥梁有限元分析[J].公路交通科技,2013,30(7):107-112.

[6]李祝龙,刘百来,李自武.钢波纹管涵洞力学性能现场试验研究[J].公路交通科技,2006,23(3):79-82.

[7]刘保东,尹航,王元丰,等.覆土波纹钢板拱桥施工过程的受力分析[J].公路交通科技,2010,27(1):50-53.

[8]尹航.覆土波纹钢板拱桥力学性能分析及设计方法研究[D].北京:北京交通大学,2008.

[9]瞿尔仁,任国红,潘莉,等.波纹钢腹板梁的结构受力与设计分析[J].合肥工业大学学报:自然科学版,2005,28(4):417-420.

[10]郭力源,李祝龙,梁养辉.荷载作用下钢波纹板小桥土压力分析[J].筑路机械与施工机械化,2013(11):56-62.

[11]李祝龙,梁养辉,黄志福,等.低路堤荷载作用下钢波纹板拱桥应变的测试研究[J].武汉理工大学学报:交通科学与工程版,2013,37(5):939-942.

[12]李晓勇,梁养辉,李祝龙,等.低路堤荷载作用下钢波纹管涵切向应变现场测试[J].公路工程,2013,38(3):90-95.

[13]JTG D60-2004,公路桥涵设计通用规范[S].

(责任编辑闫杏丽)

Strain analysis of porous corrugated steel arch bridge under vehicle loads

FANG Shi-sheng1,HUANG Zhi-fu2,ZOU Xiang-qiang1,MENG Zai-sheng1

(1.School of Civil and Hydraulic Engineering,Hefei University of Technology,Hefei 230009,China;2.Anhui Transportation Holding Group Co.,Ltd.,Hefei 230088,China)

Abstract:For the engineering project of corrugated sheet steel arch bridge in Huaibei segment of Sihong-Xuchang expressway,Anhui Province,the equivalent physical model of this bridge is built by using ANSYS software to calculate the strain of the corrugated sheet steel arch bridge under the vehicle loads. The calculated results and the measured data are compared and analyzed to verify the effectiveness and feasibility of the model. The strain variation rules under the load of highway I-level vehicle are researched on the basis of this model. The results show that under the vehicle loads,the whole of the side span positions are under tensile strain,and the strain value at the arch foot is slightly larger than those of the other positions;the strain variation rules of each measuring point position of the corrugated steel plate arch bridge do not change with the speed,while the strain values of the measuring point positions of the corrugated steel plate arch bridge are proportional to the vehicle speed.

Key words:corrugated steel plate;arch bridge;vehicle load;finite element;strain analysis

收稿日期：2015-02-05；修回日期：2015-04-10

基金项目：安徽省交通科技资助项目(AHjTkj2011-012)

作者简介：方诗圣(1962-),男,安徽岳西人,博士,合肥工业大学教授,硕士生导师.

doi:10.3969/j.issn.1003-5060.2016.06.021

中图分类号:U448.22

文献标识码：A

文章编号：1003-5060(2016)06-0823-05