OHS运输系统对VLSI厂房微振动影响分析方法

胡明祎,娄　宇,聂建国,陈　骝,窦　硕,黄　伟

(1.中国电子工程设计院,北京　100142;2.北京市微振动环境控制工程技术研究中心,北京　150080;3.清华大学 土木水利学院,北京　100084;4.合肥工业大学 土木与水利工程学院,安徽 合肥　230009;5.土木工程结构与材料安徽省重点实验室,安徽 合肥　230009)



OHS运输系统对VLSI厂房微振动影响分析方法

胡明祎1,2,3,娄宇1,2,聂建国3,陈骝1,2,窦硕1,2,黄伟4,5

(1.中国电子工程设计院,北京100142;2.北京市微振动环境控制工程技术研究中心,北京150080;3.清华大学 土木水利学院,北京100084;4.合肥工业大学 土木与水利工程学院,安徽 合肥230009;5.土木工程结构与材料安徽省重点实验室,安徽 合肥230009)

摘要:OHS运输系统是超大规模集成电路(VLSI)制造工业环境中洁净工艺系统中的重要组成部分,但是由于工业厂房的结构复杂且分布着较为密集的精密设备,OHS运输过程产生的微振动会对生产造成危害,因此需要建立合理有效的微振动控制分析方法辅助工程设计。文章基于该类工程微振动传递线性特征,利用工程实测数据,建立了振动能量封闭体简化分析模型,提出基于传递函数相似性的OHS系统微振动影响控制分析方法,并利用实际工程对该方法进行了应用说明。分析结果表明：该方法实施简单且符合现阶段工程应用需求,为OHS系统振动影响提供了合理可靠的分析手段。

关键词:OHS运输系统;超大规模集成电路;厂房;微振动影响

随着我国工业快速发展,超精密加工逐渐成为高端制造业的重要技术支柱,越来越多的高新产品需要超大规模集成电路(very large scale integrated circuit,VLSI)技术提供生产制造载体。但VLSI工艺对振动环境要求极为苛刻,当生产环境微振动水平超标,不但会导致产品制造不合格,而且改造过程还会引起巨大的经济损失。所以对VLSI生产过程中的各种振动进行控制以满足产品达标要求成为亟待解决的技术难题。

在VLSI生产过程中,影响振敏设备工作的振源有多种,由于工艺生产技术革新,出现一些新的内部工艺措施,如Over Hang System(OHS),其产生的振动与以往的振源不同,因此在设计和控制过程中需要建立合理有效的分析方法。OHS是VLSI生产工艺中的一种玻璃基板运输系统,可以做为产品存放架或者做为运输通道为各生产工艺之间提供产品,如图1所示。该运输系统在工作时产生的振动通过悬挂构件和主体结构将振动传递到振敏设备底部,从而影响设备正常作业。

图1　OHS运输系统作业过程

1振动理论分析简化模型

工业厂房振动分析方法多种多样,但直接在工程中应用仍存在很多问题,主要的原因是工业厂房振源构成复杂、传递路径多样、工业设备密集等。目前我国针对VLSI类厂房的振动控制设计规范尚不成熟,尤其缺乏合理有效的分析模型。针对该问题,大量学者在相关领域开展了很多研究工作。

文献[1]对电子工业厂房的微振动问题,建立了有限元动力分析模型,包括微振动隔振厂房的柱网、井格梁、混凝土底板、附属建筑等,并对非主要结构部分进行简化。其结论认为数值分析和实测的场地固有频率无交集,场地发生共振的可能性不大,基础设置圈梁对水平和竖向的固有频率几乎无明显影响,考虑地板下的土层和桩基础时结构的固有频率则会略有下降。文献[2]结合实际工程,对工业厂房结构振动分析模型简化进行说明,指出从振动现场的实测发现,产生共振反应的是包含梁系的一定区域,说明楼盖垂直振动具有某种程度的整体性或局部整体性。文献[3]提出非设备层楼板振动分析的两步骤法：一是通过对局部楼板模态分析,定性判断楼板是否在设备的共振区;二是采用结构-设备复合系统三维动力有限元分析模型,对非设备层楼板的动力响应进行分析。文献[4]以某水电站为例,建立混凝土重力坝厂房坝段三维整体分析模型,计算了正常运行状况下机组振动所引起厂房的动力响应,认为可能振源计算频率仅在结构个别高阶固有频率时会有共振,机组振动对结构的位移和应力影响较小,对厂房的安全运行影响不大。

此外,文献[5]提出了一种利用结构自身提供控制力“以振制振”的轻钢结构工业厂房振动自控方案,建立了体系动力分析模型。文献[6]通过引入黏弹性人工边界,建立了桩-土-结构相互作用的厂房整体有限元分析模型,对设备作用下的多层厂房振动进行较为全面的分析,并就模型简化及桩-土体系对系统的影响进行对比研究。文献[7]对三峡电站厂房结构进行了等效振源、阻尼等模型参数确定,分析了厂房结构在各种振源联合作用下的动力响应。

本文基于上述文献成果,研究OHS系统运输对厂房内精密设备产生微振动的控制分析方法。简化分析模型包括如下4个部分:地基基础、厂房主体结构、OHS悬挂及运行装置、防微振基台,如图2所示。图3所示为OHS运输过程结构微振动分析模型示意图,系统中主要振动源为OHS运输装置,振动能量的传递路径主要是通过轨道梁、悬挂结构、结构主梁和防微振基台,进而传递到振敏设备上。此外由于微振动低频微幅特征,本文中考虑了地基基础黏弹性边界的影响[8],并根据实验数据确定了OHS的悬挂系统传递参数,通过基台形状、位置和边界条件合理设计,进行微振动响应有效预估。

在分析模型中,主要动力参数包括如下4类：地基基础的黏弹性边界参数、厂房主体结构参数、OHS悬挂系统和防微振基台参数等。其中黏弹性边界的刚度K1、阻尼C1按照三维黏弹性人工边界方法[8]进行取值;厂房主体结构只考虑主框架梁和柱,可根据工业厂房设计参数进行刚度K2、阻尼C2取值,也可以通过动刚度测试结果进行取值;OHS悬挂系统的刚度K3和阻尼C3主要通过单独的实验测试或扫频结果进行取值;防微振基台的设计参数的刚度K4、阻尼C4可以通过出厂实验或现场动刚度扫频实验进行取值。

图2　OHS运输过程VLSI厂房结构微振动传递原理图

图3　OHS运输过程结构微振动分析模型

2OHS微振动分析方法

VLSI工业厂房的主体结构一般采用钢筋混凝土框架结构,其OHS系统工作过程中,振源是稳定的,微振动在结构中的传递具有线性特征。针对该问题,首先根据图3建立OHS系统微振动动力方程,即

(1)

(2)

其中,Tj→k(ωi)为j点到k点振动第i阶模态下传递函数值;Rk(ωi)为k处第i阶模态下振动值;Rj(ωi)为j点第i阶模态下振动值;ηi为第i阶模态修正系数。(2)式说明可通过2点间的振动频响比值获取传递函数,数据来源包括经验公式、FE分析和已建结构微振动测试。所以在工程中,可通过线性叠加获取k点总响应Rk(ω),即

(3)

其中,Fj(ωi)为j质量点第i阶模态下有效荷载,通过上述方法可获取k点的振动响应。由于VLSI制造工艺中存在大量的曝光机等精密设备,其对速度具有较强敏感性,所以本文以速度为控制标准进行振动控制分析方法推导,计算结果采用VC曲线作为评比标准。对于各阶模态下有效质量点振动响应也可以进行计算,假设分析模型属于一个能量封闭体,有效振源和振动影响点均分布在该能量封闭体内部。根据封闭体中能量守恒,建立(4)式:

(4)

其中,W为能量封闭体中由OHS运输产生的振动动能总和;mj(ωi)为第j质量点第i阶模态下参振质量；vj(ωi)为第j质量点第i阶模态下振动速度;S为模型质量点总数;N为截取有效模态阶数。

为了有效实现封闭体中第k质量点第i阶模态下的振动速度满足容许振动控制标准,可以根据(4)式等效建立该点速度的控制方程,即

(5)

3OHS微振动控制分析方法应用

本文利用上述方法对某VLSI项目中OHS运输微振动工程控制进行了分析。由(5)式可知,在OHS微振动控制设计过程中,可以采用如下2种方法以减小设备安装位置的振动影响vk(ωi):① 提高mk(ωi),在工程中采用的方法是增大防微振基台的有效质量;② 进行合理有效的结构设计,在封闭体总质量不变的情况下,调整主体结构K1、K2、K3等参数设计值使得结构模态分布发生变化,减小k质量点第i阶模态下能量消耗。总之,可以通过增大基台质量或优化整体结构模态设计进行微振动控制。

根据上述方法,本文采用传递函数方法确定结构在振动环境下的响应,建立工程测试数据库和数值模型库,进行频域计算和时域计算复核校验。图4所示为基于传递函数相似性的电子工业厂房微振动分析方法流程图。

图4　基于传递函数相似性的电子工业厂房微振动控制分析方法

基台振动传递函数特征如图5所示，基台式华夫板FE模型如图6所示，主体结构有限元模型如图7所示。

根据图4本文利用已建结构和待建结构的微振动传递函数相似性,建立了OHS运输过程中振动响应等效计算方法。

系统主要用于Stocker和支撑之间的传送,其中装运架质量300 kg,运输车质量370 kg,悬挂轨道60 kg/m,悬挂构件高度1.2 m,最大加速度0.5 m/s2,正常匀速为3 m/s。项目拟采用防微振基台设计方案进行微振动控制,其中基台长×宽×高为5 000 mm×2 500 mm×300 mm,微振动容许振动值为2～100 Hz频段内幅值小于12.5 μm/s(VC-C标准)。根据工艺要求其悬挂系统运输工况分为如下3种：装载、卸载和输送。通过实验室车载运输实验得到装载工况下OHS运输过程产生的振动影响最大,OHS悬挂系统顶部结构主梁振动加速度可达竖直向0.1 m/s2,水平向0.5 m/s2。

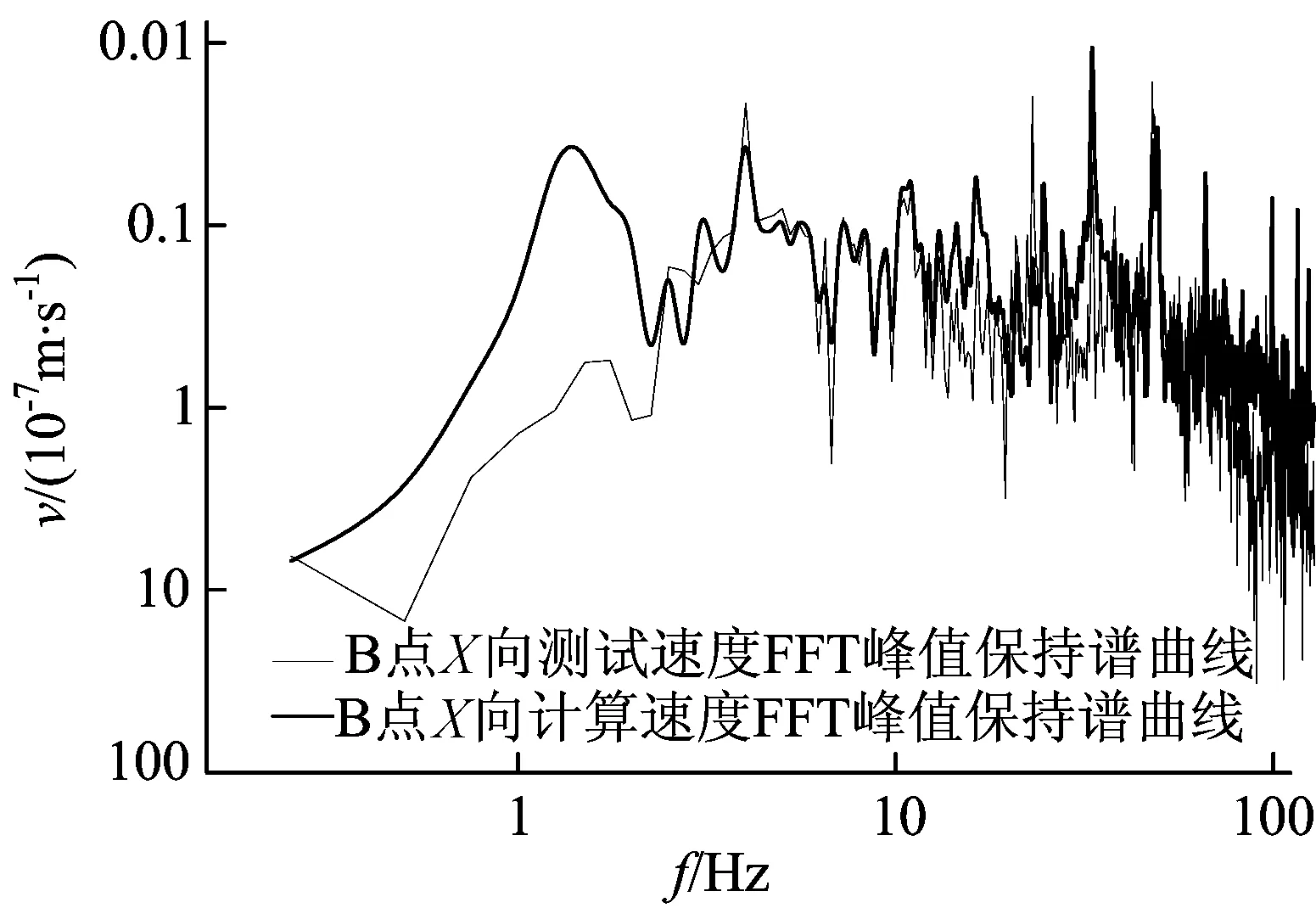
图5　基台振动传递函数特征

图6　基台式华夫板FE模型

图7　主体结构有限元模型

根据工程概况信息,本文以OHS装载工况振动影响为计算内容,结合传递函数相似性和电子厂房振动衰减工程经验,利用本文方法进行各阶段传递函数计算和控制效果对比验算。

利用(2)式,结合相似工程数据可以对从主体结构钢梁悬挂点处至防微振基台的传递函数进行计算,结果如图8所示，从图8可以看出,3个方向的传递率大多数都在1.0以内,X、Y、Z向的平均传递率分别为0.22、0.24、0.20。从频域分布情况看,Z向60 Hz以内有局部传递率大于1,最高在5.2 Hz处达到2.7;X向20 Hz以内有局部传递率大于1,最高在12.4 Hz处达到2.4;Y向10～60 Hz、85～95 Hz范围有局部传递率大于1,最高在90 Hz处达到2.1。

图8　X、Y、Z向基台传递曲线

总体上可以看出，微振动从主体结构钢梁顶部至防微振基台的传递降幅可达80%左右。同理,利用(2)式可以获取传递路径上任意相邻2点的传递函数,最终利用(3)式可以获取OHS运输过程中防微振基台的振动影响水平,如图9所示。

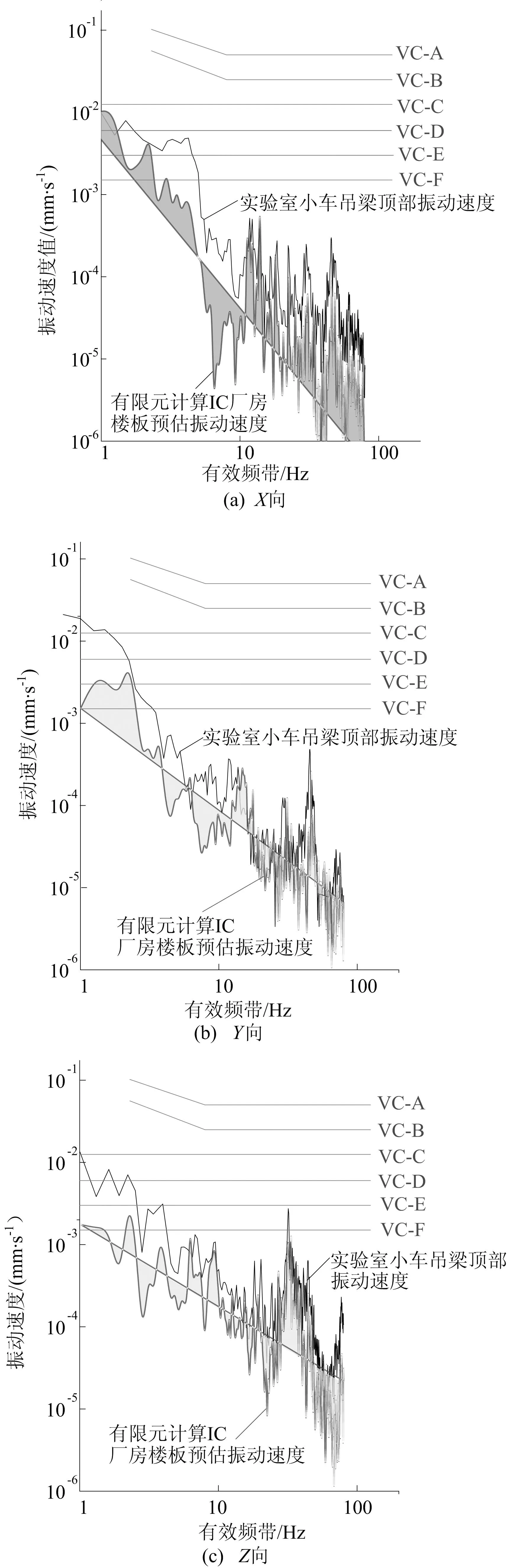
图9　X、Y、Z向减振效果对比

由图9可知,有限元计算结果和实验室实测结果相比,10 Hz以下略低,10 Hz以上较为吻合,这是因为在本文中模态修正系数ηi值均取值为1,未进行详细对比分析。

4结论

在VLSI工业工程建设中,OHS运输系统是重要的工艺构成部分,随着技术发展,其微振动影响越来越突出,需要科学合理的分析方法,对复杂振动现象进行解释,并有效辅助设计。本文建立了振动能量封闭体简化分析模型,结合微振动控制措施,提出基于传递函数相似性的OHS系统微振动影响控制分析方法,得到以下结论:

(1)OHS振动分析问题可按照线性振动假设进行模型简化。简化分析模型应包括地基基础、厂房主体结构、OHS悬挂装置、防微振基台,并假设分析模型属于一个能量封闭体。

(2)主体结构钢梁顶部至防微振基台的振动传递降幅可达80%左右。

(3)利用微振动线性特征,通过线性叠加获取影响点总响应，与试验结果相比,10Hz以下分析结果略低,10Hz以上结果较为吻合,需要对模态修正系数ηi进行合理取值。

(4)本文方法利用已建工程相似数据库,从控制技术角度而言,便于进行OHS影响振动控制;从分析效率角度而言,方法简单高效,为OHS微振动控制辅助设计提供了理论依据。

[参考文献]

[1]高广运,张博,李宁.电子工业厂房微振动测试及数值分析[J].勘察科学技术,2011(3):51-55.

[2]邱德修,樊开儒.多层工业厂房的振动问题分析[J].工业建筑,2010,40(Z1):511-513.

[3]冯军和,张敏政,闫维明.多层选煤厂房的受振层楼板振动分析[J].地震工程与工程振动,2007,27(2):99-103.

[4]武颖利,蔡新,李洪煊,等.机组振动下电站厂房共振校核和动力响应分析[J].人民黄河,2010,32(10):141-143.

[5]王宏伟,陈啸,刘斌,等.基于内置激振源轻钢结构振动自控体系研究[J].工业建筑,2007,37(Z1):719-723.

[6]冯军和,闫维明.考虑桩-土-结构相互作用影响的多层厂房振动分析[J].工业建筑,2008,38(Z1):438-442.

[7]欧阳金惠,陈厚群,李德玉.三峡电站厂房结构振动计算与试验研究[J].水利学报,2005,36 (4):484-490.

[8]刘晶波,谷音,杜义欣.一致粘弹性人工边界及粘弹性边界单元[J].岩土工程学报,2006,28 (9):1070-1075.

(责任编辑张镅)

Method for analyzing influence of OHS transport system on micro-vibration of VLSI structure

HU Ming-yi1,2,3,LOU Yu1,2,NIE Jian-guo3,CHEN Liu1,2,DOU Shuo1,2,HUANG Wei4,5

(1.China Electronics Engineering Design Institute,Beijing 100142,China;2.Micro-vibration Environmental Control Engineering Technology Research Center of Beijing,Beijing 150080,China;3.School of Civil Engineering,Tsinghua University,Beijing 100084,China;4.School of Civil and Hydraulic Engineering,Hefei University of Technology,Hefei 230009,China;5.Anhui Key Laboratory of Structure and Materials in Civil Engineering,Hefei 230009,China)

Abstract:During the industrial manufacture of very large scale integrated circuit(VLSI),Over Hang System(OHS)is very important part of the clean technology system. However,many precision devices are generally densely distributed in the industrial plant which is characterized with complex structure type,micro-vibration made by OHS operation will do harm to the manufacture,so it is necessary to create reasonable and effective analysis method for micro-vibration control design. In this paper,based on the linear transfer characteristic and the engineering test data,the simplified model of vibration energy closure is built,and the analysis method for the micro-vibration control of OHS system is proposed and then illustrated by the application in real project. The results show that the method,in accordance with engineering requirement at present,is easy to be carried out,and it provides a reliable method to solve the influence of OHS system.

Key words:Over Hang System(OHS);very large scale integrated circuit(VLSI);plant;micro-vibration influence

收稿日期：2015-08-05；修回日期：2015-08-27

基金项目：北京市科学技术委员会资助项目(Z131101002813083)

作者简介：胡明祎(1982-),男,河南固始人,博士,中国电子工程设计院工程师.

doi:10.3969/j.issn.1003-5060.2016.06.019

中图分类号:TU311.3

文献标识码：A

文章编号：1003-5060(2016)06-0812-06