基于概率统计源强的河道多点疏浚工程悬浮物影响预测方法

计　红,韩龙喜

(1.安庆师范大学 资源环境学院,安徽 安庆　246011;2.河海大学 环境学院,江苏 南京　210098)



基于概率统计源强的河道多点疏浚工程悬浮物影响预测方法

计红1,韩龙喜2

(1.安庆师范大学 资源环境学院,安徽 安庆246011;2.河海大学 环境学院,江苏 南京210098)

摘要:文章提出在采用数学模型法研究河道多点疏浚工程施工期的悬浮物影响时,首先对悬浮物排放特征进行概化,得到不同概率下的源强组合，然后通过建立悬浮物影响预测数学模型,计算不同概率组合工况下悬浮物质量浓度的时空分布，最后对分析断面的悬浮物影响做进一步的统计特征分析。与现有的研究方法相比,该方法更为合理、全面地反映了多点疏浚产生的悬浮物对水环境质量的时空影响,从而为水环境保护及管理提供更为可靠的科学依据。

关键词:河道疏浚;悬浮物影响;数学模型

河道疏浚能改善水流条件,优化河流水质,提高河道的行洪和通航能力,但疏浚会造成局部水体悬浮物含量增加,水体透明度降低,进而影响水生生物的栖息、生长和繁殖[1]。

大量研究表明,水体中的悬浮物对鱼类会产生致死效应、亚致死效应及行为影响[2-3],分别表现为直接杀死鱼类个体,降低鱼类生长率及其对疾病的抵抗能力,干扰其产卵、改变其洄游习性,最终导致其孵化率、仔鱼成活率、饵料生物的丰度及捕食效率的降低。因此,在河道疏浚工程环境影响评价过程中,必须对施工期悬浮物的影响程度和范围进行预测,以作为水生态环境保护及管理的依据。

在采用数学模型定量分析疏浚工程施工期的悬浮物影响时,源强是影响预测结果的主要参数之一。源强的大小取决于污染源的排放方式及污染源的个数。受工程规模及自然条件、人员配备、机械设备等施工条件的制约,某些疏浚工程会采用划分不同疏浚区分别作业的方式进行,如安徽省涡河近期治理工程(一期)大寺—义门段河道疏浚工程划分了3个作业区,疏浚区间总长分别为6 052.7、4 656.4、3 703.3 m。对于这样的多点疏浚工程,可能出现不同疏浚点同一时段处于不同施工状态的情况,形成不同的组合工况。以往的研究在分析该类工程的悬浮物影响时,要么只分析单个疏浚点造成的悬浮物浓度变化[4-6],无法考量多点疏浚对水生态环境在空间上的整体效应;要么将每个疏浚点产生的悬浮物都处理成连续排放的污染源,预测多点疏浚的最大不利影响[7-10],无法真实反应悬浮物水环境效应的时间变化特征。

本文针对多点施工的河道疏浚工程,认为疏浚悬浮物属于有固定时间间隔的间歇排放的污染源,基于疏浚源强的概率统计特征,构建基于悬沙迁移特性的悬浮物影响预测数学模型,进行不同概率组合工况下的悬浮物影响数值模拟,经统计分析得到分析断面悬浮物质量浓度增量的概率分布特征,为该类疏浚工程的环境管理提供更可靠、全面的科学依据。

1多点疏浚污染源排放统计特征概化

对于时间连续型污染源,污染源排污强度概化为随时间不变的恒定源强;而对于间歇排放的污染源,则根据其排放规律,采用概率统计的方法进行概化。

假定某疏浚工程有n个疏浚点,Ti为疏浚点i的施工时段。对于每一时刻t,当t∈Ti时,认为疏浚点i是排污的,否则；认为疏浚点i不排污。

根据分析时段内各时刻疏浚点i是否排污,可以得到不同的排污组合工况,其中某一工况j出现的概率为:

(1)

其中,n为所有工况的总次数;nj为某一工况出现的次数。

t时刻各疏浚点源强Si计算公式为[5]:

(2)

其中,S0为悬浮物发生系数;R为指定发生系数S0时悬浮物粒子粒径累积百分比;R0为现场流速悬浮物界限粒子累积百分比;T为疏浚量。

2悬浮物影响预测数学模型

基于平面二维悬沙对流扩散方程构建的悬浮物影响预测数学模型为:

其中,h为水深;u、v分别为深度平均流速在x、y向的流速分量;ρ为沿水深平均的悬浮物质量浓度;εx、εy分别为x、y向的悬浮物紊动扩散系数;Ws为沉速，采用Van Rijn公式计算[11]。

3环境影响统计特征分析

基于多点疏浚的污染源排放统计特征,利用悬浮物输移扩散数学模型可预测得到计算时段内不同概率组合工况下的悬浮物质量浓度增量空间分布及分析断面悬浮物质量浓度增量的时间变化过程。然而,疏浚工程对重要河道断面的悬浮物影响在不同质量浓度范围出现的概率,也是管理者颇为关注的问题。

假设工程引起的某一断面的悬浮物质量浓度增量位于区间[ρ1,ρ2]的总概率为ps,则有:

(3)

其中,pj为某一组合工况j出现的概率;βj为判断系数,当预测时段内工况j引起的断面的质量浓度增量落于区间[ρ1,ρ2]时,βj=1,否则,βj=0。

4案例研究

4.1研究区域及施工方案设计

选择某工程1 000 m的疏浚河段为研究对象进行案例研究。假设该工程的疏浚施工分为3个疏浚区,对应的河段长度分别为200、600、200 m,每个疏浚区使用1台200 m3/h的绞吸式挖泥船。由于绞吸式挖泥船为定点作业[12],故不考虑挖泥船在计算时段内位置的变化,将每个疏浚点概化为一个固定的点源,设置于疏浚区中心的一个计算网格上。疏浚点(P1、P2、P3)位置及分析断面(S1～S6)分布如图1所示。

施工期每天的作业时间为7:00-19:00,受现场施工条件的限制,3个疏浚区制定了不同的施工方案,见表1所列。

图1　疏浚点及分析断面位置示意图

疏浚区编号施工时间工作时间17:00-15:00连续工作8h27:00-12:0014:00-19:00每班连续工作5h37:00-9:0010:00-12:0013:00-15:0017:00-19:00每班连续工作2h

4.2污染源排放概率统计结果

不同组合工况的概率统计结果如下：

(1)1点独排。P1独排，359次，概率为8.3%；P2独排，719次，概率为16.7%；P3独排工况不会出现。

(2)2点同排。P1、P2同排，359次，概率为8.3%；P1、P3同排，360次，概率为8.3%;P2、P3同排，721次，概率为16.7%。

(3)3点同排。P1、P2、P3同排，1 803次，概率为41.7%。

在计算时段(7:00—19:00)内,3个疏浚点同时排污的概率最高,为41.7%；共有6种工况,分别为点1独排、点2独排、点1和点2同排、点1和点3同排、点2和点3同排以及3点同排。

4.3模型参数取值及定解条件

采用悬浮物影响预测数学模型计算不同概率组合工况下的悬浮物质量浓度增量场,疏浚源强Si根据(2)式确定。

根据施工方案,模拟时长取12 h(7:00—19:00),时间步长设为10 s。假设产生的悬浮物为非黏性泥沙,中值粒径取D50=0.025 mm,悬浮物密度ρs=2 650 kg/m3,孔隙率n=0.4。河床糙率、沉降速率、悬浮物扩散系数、水流挟沙能力等参数的取值采用经验公式计算加以确定。

计算区域悬浮物初始质量浓度设为0，入流边界悬浮物质量浓度也设为0。

4.4施工期悬浮物影响分析

(1)不同组合工况下的悬浮物质量浓度增量。6种工况下的悬浮物质量浓度增量分布情况如图2所示。

依据图2的预测结果,不同概率工况下6个分析断面的悬浮物质量浓度增量如图3所示。由图3可知,在最高概率(41.7%)工况,即3个疏浚区同时排污的情况下,断面1～断面6的悬浮物质量浓度增量分别为9.2、5.1、3.8、6.3、3.5、21.9 mg/L。

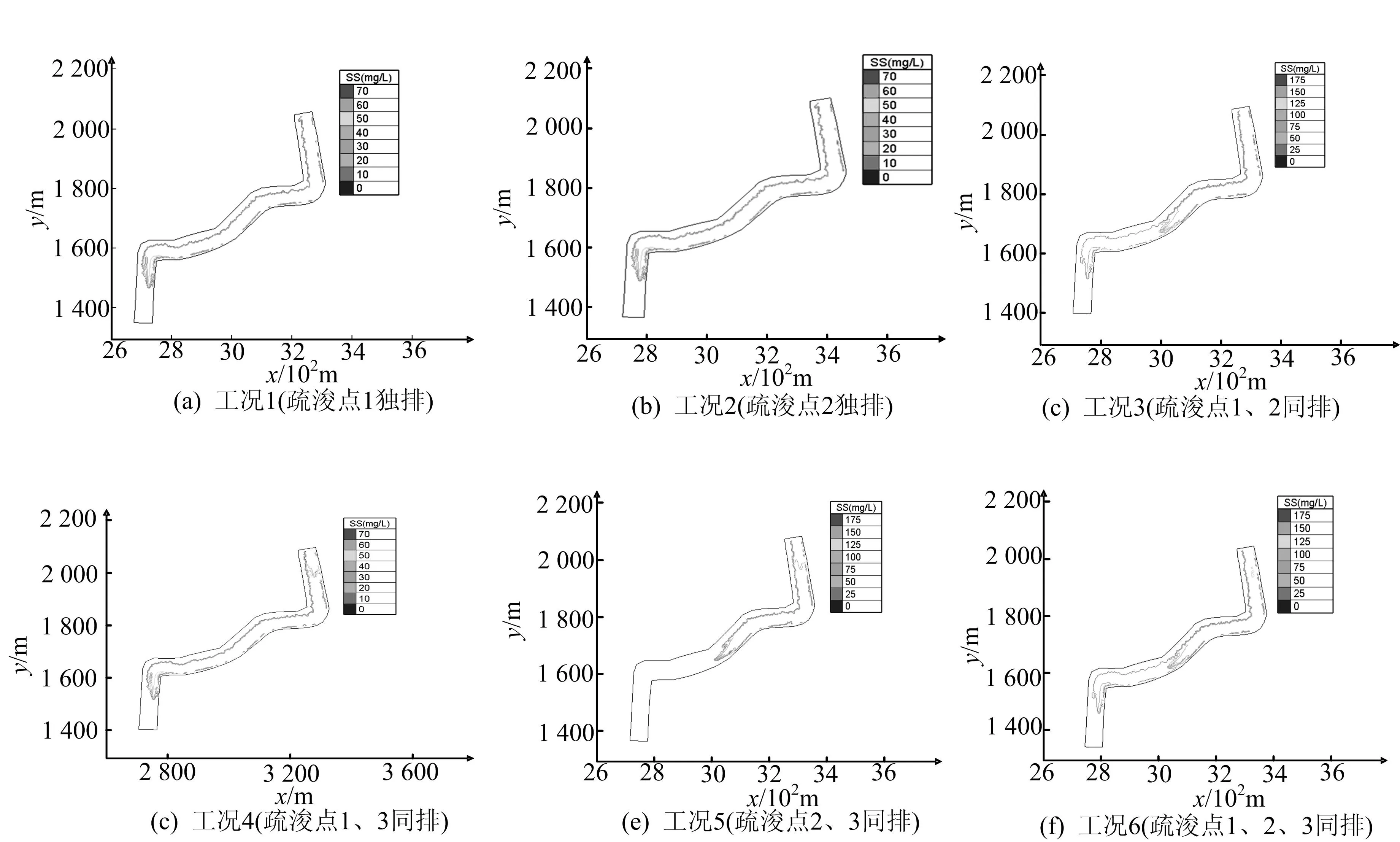
图2　各工况下悬浮物质量浓度增量分布图

此外,各分析断面在预测时段内的质量浓度增量时间变化过程如图4所示。

(2)分析断面悬浮物质量浓度增量统计特征。由图2～图4的预测结果,将疏浚工程影响下的悬浮物质量浓度增量划分为0～5 mg/L、5～10 mg/L、10～15 mg/L、15～20 mg/L、20～25 mg/L 5个等级,并依据各工况的概率对各分析断面的悬浮物质量浓度增量进行概率统计。

断面1～断面6在各工况协同作用下的悬浮物质量浓度增量概率分布如图5所示。由图5可知,在预测时段内,断面3和断面5的悬浮物质量浓度增量不会超过5 mg/L;断面1、断面2、断面4的悬浮物质量浓度增量不会超过10 mg/L,其中断面1和断面2的悬浮物质量浓度增量在5～10 mg/L范围内的概率为66.6%,断面4的悬浮物质量浓度增量在5～10 mg/L范围内的概率为83.4%;断面6水质受疏浚工程影响最大,悬浮物质量浓度增量在10～25 mg/L范围内的概率为66.7%,质量浓度增量在0～5 mg/L范围内的概率只占33.3%。

工况

图4　分析断面平均质量浓度时间变化过程

图5　各工况协同作用下断面质量浓度增量概率分布

5结束语

本文针对多点施工的河道疏浚工程,对于按一定规律间歇排放的悬浮物污染源,提出用概率统计的方法对污染源排放特征进行概化,得到不同概率下的源强组合,进而建立悬浮物影响预测数学模型,计算不同概率组合工况下悬浮物质量浓度的时空分布,并获得工程对分析断面的悬浮物质量浓度影响的统计特征。

与目前常见的多点疏浚工程悬浮物影响预测相比,本文方法能更客观、全面地为工程管理及环境管理部门提供决策依据。

由于本文旨在提出一种预测多点疏浚工程悬浮物影响的方法,对于案例研究中的数学模型并未进行参数率定,将在今后的研究中加以完善。

[参考文献]

[1]范学平,曾德付. 沿江施工产生悬浮物对环境影响分析[J]. 交通环保,2004(6): 10-12.

[2]Reynolds J B,Simmons R C,Burkholder A R. Effects of placer mining discharge on health and food of arctic grayling[J]. JAWRA Journal of the American Water Resources Association,1989,25(3): 625-635.

[3]Newcombe C P,Macdonald D D. Effects of suspended sediments on aquatic ecosystems[J]. North American Journal of Fisheries Management,1991,11(1): 72-82.

[4]郭珊,杨卫军,黄伟杰,等. 疏浚悬浮物对海洋环境影响的数值模拟[J]. 黑龙江水专学报,2009,36(4): 58-61.

[5]刘俊勇,徐峰俊,朱秋菊. 珠江口门近期整治工程对含氯度影响及施工期悬浮物输送数学模型研究分析[J]. 人民珠江,2006(6): 45-47.

[6]陈小红,涂新军. 深圳湾游艇项目悬浮物影响预测与分析[J]. 海洋环境科学,2000(1): 48-51.

[7]贾怡然,孙英兰,张学庆. 港池疏浚过程悬浮物影响预测研究及应用[J]. 港工技术,2007(3): 3-5.

[8]郑志华,徐碧华. 航道疏浚中悬浮泥沙对海水水质和海洋生物影响的数值研究[J]. 上海船舶运输科学研究所学报,2008,31(2): 105-110.

[9]骆育敏,梁明易,王朝晖,等. 珠江三角洲陈村水道航道整治对该区域水环境影响评价[J]. 暨南大学学报:自然科学与医学版,2002,23(5): 88-94.

[10]赵吉国,黄锦林. 汕尾电厂进港航道疏浚悬浮物扩散数值模拟[J]. 广东水利水电,2010(10): 24-25.

[11]Van Rijn,Leo C.Principles of sediment transport in rivers,estuaries and coastal seas[M]. Amsterdam: Aqua Publications,1993：85.

[12]戴明新.挖泥船疏浚作业对环境影响的试验研究[J]. 交通环保,1997(4):7-9.

(责任编辑张镅)

Predicting method for the impact of suspended solids from multi-point river dredging based on probability statistical source intensity

JI Hong1,HAN Long-xi2

(1.School of Resources and Environment,Anqing Normal University,Anqing 246011,China;2.College of Environment,Hohai University,Nanjing 210098,China)

Abstract:This paper focuses on the study of the impact of suspended solids from multi-point river dredging projects by using the mathematical model method. Firstly,the statistical characteristic of pollutant sources is generalized to obtain different combined construction schemes under different probabilities. Secondly,the mathematical model based on the transportation features of suspended solids is established to predict the temporal and spatial distribution of suspended solids under the different schemes. Finally,the probability features of increments of suspended solids at the control sections are analyzed. Compared with the existing research methods,the method proposed in the paper can reflect the temporal and spatial impact of suspended solids from multi-points dredging on water quality a more reasonably and comprehensively and provide a more reliable scientific basis for water environment protection and management.

Key words:river dredging;suspended solids impact;mathematical model

收稿日期：2015-02-27；修回日期：2015-07-23

基金项目：水利部公益性行业专项经费资助项目(201001028)

作者简介：计红(1982-),女,安徽东至人,博士,安庆师范大学讲师; 韩龙喜(1964-),男,江苏扬州人,博士,河海大学教授,博士生导师.

doi:10.3969/j.issn.1003-5060.2016.06.018

中图分类号:X828

文献标识码：A

文章编号：1003-5060(2016)06-0807-05