基于马氏切换Cohen-Grossberg神经网络输入到状态稳定的新判据
2016-07-18李志鸿何秀丽
李志鸿,何秀丽
(河海大学 理学院,江苏 南京 210098 )
基于马氏切换Cohen-Grossberg神经网络输入到状态稳定的新判据
李志鸿,何秀丽
(河海大学 理学院,江苏 南京 210098 )
摘要:针对具有马氏切换的Cohen-Grossberg神经网络的稳定性问题,应用Lyapunov函数理论和Halanay不等式技巧,提出了神经网络输入到状态稳定性的新判据,并通过数值例子来验证所得结论的正确性和有效性.
关键词:Cohen-Grossberg神经网络; 输入到状态稳定; 马氏切换;Halanay微分不等式
1983年,Cohen和Grossberg提出了一种神经网络模型[1],被称为Cohen-Grossberg神经网络,由于其广泛应用在不同领域,如模式识别、记忆与信号处理、图象处理与计算技术等领域,因而得到了高度的重视.但是在实际应用中输入、切换是不可避免的,这些因素往往导致整个系统的震荡,甚至不稳定. 因此有关输入[2-4]、切换[5-6]Cohen-Grossberg神经网络的研究已逐渐引起学者的关注. 最常见的切换就是马氏切换[7,10],研究带有马氏切换的神经网络的稳定性问题具有极其重要的意义. 本文推广了Halandy不等式[8],构造了更一般的Lyapunov函数,得出的主要结果改进和推广了已有文献的一些结论[9-10],不但推导出模型指数输入到状态稳定的新判别准则,而且给出解的指数收敛速度的估计.
1模型和预备知识
考虑Cohen-Grossberg神经网络模型

(1)
其中,k=1,2,…,n,n 表示网络中神经元的个数,xk(t)表示第k个神经元在t时刻的状态,hk表示放大函数,dk表示适当的行为函数,A(i)=(akl(i))n×n和B(i)=(bkl(i))n×n分别表示连接权矩阵和时滞连接权矩阵,fl为神经元的激励函数,uk(i,t)表示网络的一些外部输入,τ(t)表示时滞,且满足条件0≤τ(t)≤τ,τ′(t)≤ρ<1,τ和ρ都是正常数.
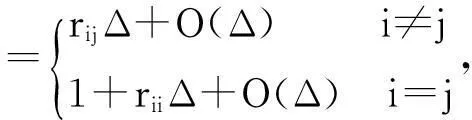
LV(x(t),t,i)=Vt(x(t),t,i)+Vx(x(t),t,i)×{H(x(t))[-D(i,x(t))+
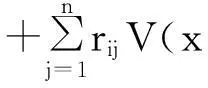

要求神经网络模型(1)满足以下假设



定义1[9]若存在一个KL—函数β:R+×R+→R+和一个K—函数γ(·)使得x(t;ξ,u(t))满足
|x(t;ξ,u(t))|≤β(t,‖ξ‖τ)+γ(‖u‖∞)
则称系统(1)是输入到状态稳定的.
定义2[9]若存在一个常数λ>0和2个K—函数β,γ使得x(t;ξ,u(t))满足
|x(t;ξ,u(t))|≤β(‖ξ‖τ)exp(-λt)+γ(‖u‖∞)
则称系统(1)是指数输入到状态稳定的.
定义3[11]设g是R→R的连续函数,g的Dini-导数可表示为

2稳定性分析

D+V(r(t),x(t))≤-α1V(r(t),x(t))+α2V(r(t-τ),x(t-τ))+γ(|u|[0,t]),
(2)
那么

(3)

如果上式不成立,则必然存在t*使得
由定义3,有



x(t*))≤-α1EV(r(t*),x(t*))+α2EV(r(t*-τ),x(t*-τ))+(α1-α2)γt*.
(7)
由式(5)有,EV(r(t*),x(t*))-γt*=V(r(0),x(0))exp(-λ*t*). 又由式(4)有,W(r(t*-τ),x(t*-τ))≤H(r(t*-τ),x(t*-τ))=V(r(0),x(0))exp(-λ*(t*-τ))=V(r(0),x(0))exp(λ*τ)exp(-λ*t*),即EV(r(t*-τ),x(t*-τ))-γt*-τ≤V(r(0),x(0))exp(λ*τ)exp(-λ*t*). 因此,把以上2式分别代入式(7)得
D+W(r(t*),x(t*))≤-α1[EV(r(t*),x(t*))-γt*]+α2[EV(r(t*-τ),x(t*-τ))-γt*]≤-
α1V(r(0),x(0))exp(-λ*t*)+α2V(r(0),x(0))exp(λ*τ)exp(-λ*t*)(-α1+α2exp(λ*τ)V(r(0),x(0))exp(-λ*t*))<-
λ*V(r(0),x(0))exp(-λ*t*))=D+H(t*).
与式(6)矛盾, 故式(3)成立.
证毕.
定理1在假设1~4之下,如果存在正定矩阵S(l)和正对角矩阵P(l)=diag{p1(l),p2(l),…,pn(l)},Q(l)=diag{q1(l),q2(l),…,qn(l)}, 使得
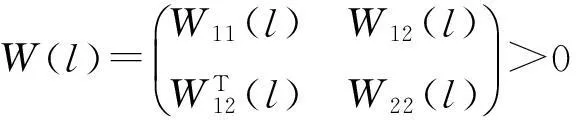
并且c1δ2>c2ητ2,那么系统(1)是输入到状态稳定的,其收敛率至少是λ/2,其中
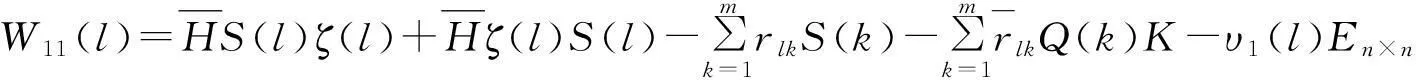



证明考虑如下Lyapunov函数

(8)
由式(8)可得
c1|x|2≤V(x(t),l)≤c2|x|2,
(9)
根据假设1~4以及LV的定义,有
LV(x(t),l)=2xT(t)S(l)[H(x(t))(-D(l,x(t))+A(l)f(x(t))+B(l)f(x(t-τ(t)))+u(l,t))]+

2xT(t)S(l)[H(x(t))(-D(l,x(t))+A(l)f(x(t))+B(l)f(x(t))+u(l,t))]+
2fT(x(t))Q(l)[H(x(t))(-D(l,x(t))+A(l)f(x(t))+B(l)f(x(t))+u(l,t))]+
2xT(t)S(l)H(x(t))B(l)(f(x(t-τ(t))-f(x(t)))+2fT(x(t))Q(l)H(x(t))B(l)×

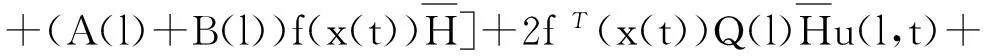
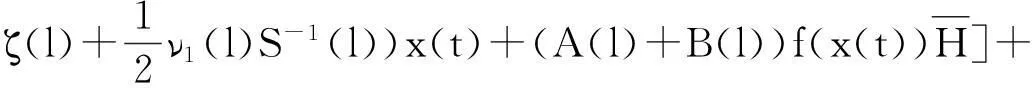



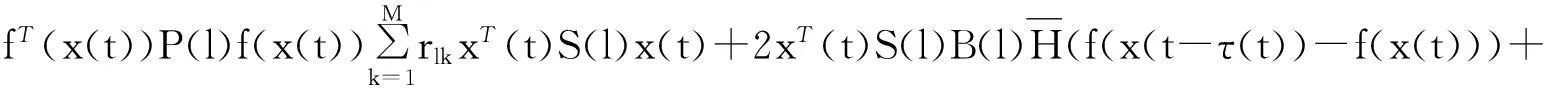
(xT(t),fT(x(t)))W(l)(x(t),f(x(t)))+δ|x(t)|2+2δ|f(x(t))|2+

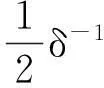




由式(1)可得

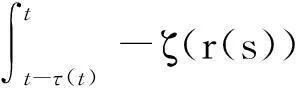





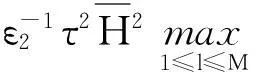


利用广义Ito公式把上式代入式(10)可得

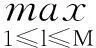
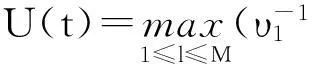
根据引理1,得

.

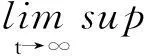
证毕.
3数值例子
考虑带有时滞的二阶Cohen-Grossberg神经网络系统


h1(x1(t))=0.9+0.1sinx1(t),h2(x2(t))=0.7+0.3cosx2(t),


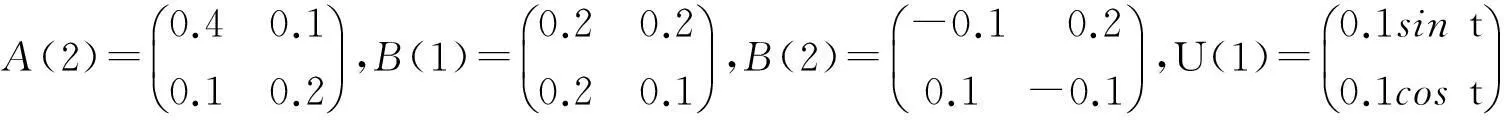

取τ(t)=0.8≤τ=1,可以计算出


c1=2,c2=2.22,δ=4.15,α1=1.87,α2=0.32.
显然,α1>α2, 满足引理1的所有条件.模拟表明,图1是输入到状态稳定的;当没有输入时,图2也是稳定的,因此系统(1)是输入到状态稳定的.

参考文献:
[1] Cohen M A, Grossberg S. Absolute stability of global pattern formulation and parallel memory storage by competitive neural networks [J].IEEE Trans.Syst.Man Cybern.SMC, 1983,13(4):815-826.
[2] Yang Z C, Zhou W S, Huang T W. Exponential input-to-state stability of recurrent neural networks with multiple time-varying delays [J].Cogn Neurodyn,2014,8(9):47-54.
[3] Zhu Q X, Cao J D, Rakkiyappan R. Exponential input-to-state stability of stochastic cohen-grossberg neural networks with mixed delays [J].Springer Nonlinear Dyn,2015,79(2):1 085-1 098.
[4] Zhu S, Shen Y. Two algebraic criteria for input-to-state stability of recurrent neural networks with time-varying delays [J]. Neural Comput Applic,2013,22(9):1 163-1 169.
[5] Choon K A. Passive learning and input-to-state stability of switched Hopfield neural networks with time-delay [J]. Information Sciences,2010,180:4 582-4 594.
[6] Xu Y, Luo W W, Zhong K, et al. Mean square input-to-state stability of a general class of stochastic recurrent neural networks with markovian switching [J].Neural Comput Applic,2014,25(2):1 657-1 663.
[7] Huang H, Ho D W C, Qu Y Z. Robust stability of stochastic delayed additive neural networks with markovian switching [J]. Neural Netw, 2007, 20(5):799-809.
[8] Halanay A. Differential equations: stability, oscillation, timelags [M].New York: Academic,1966.
[9] Zhou W S, Teng L Y, Xu D Y. Mean-square exponentially input-to-state stability of stochastic cohen-grossberg neural networks with time-varying delays [J].Neurocomputing,2015,153(4):54-61.
[10] Shen Y, Wang J. Almost sure exponential stability of recurrent neural networks with markovian switching [J]. IEEE Transactions on neural networks,2009,20(5):840-855.
[11] Liao X X, Luo Q, Zeng Z G, et al. Global exponential stability in Lagrange sense for recurrent neural networks with time delays [J].Nonlinear Analysis: Real World Applications,2008,9(3):1 535-1 557.
[12] Mao X, Yuan C. Stochastic differential equations with markovian switching [M].London: Imperial College Press,2006.
Input to State Stability Based on Cohen-Grossberg Neural Network with Markovian Switching
Li Zhihong, He Xiuli
(College of Science, Hehai University, Nanjing 210098, China)
Abstract:Aimed at the stability of Cohen Grossberg neural networks with Markovian switching, in the report, Lyapunov-Krasovskii functional method and Halanay differential inequalities technique were used, and the new criteria on the input to the state stability of neutral network was proposed. Lastly, the numerical examples were used to illustrate the correctness and efficiency of the results.
Keywords:input to state stability; Cohen-Grossberg neural networks; Halanay differential inequalities; Markovian switching
收稿日期:2015-11-04
基金项目:中央高校科研业务费青年教师科研创新能力培育项(A)(2015B19814)
作者简介:李志鸿(1992-), 女, 江苏泰州人,河海大学2014级硕士研究生, 研究方向:神经网络的稳定性分析,E-mail:1353285605@qq.com. 通信作者: 何秀丽(1979-), 女, 湖北黄冈人,博士研究生, 讲师, 研究方向:随机动力系统,E-mail:hexiu00@163.com
文章编号:1004-1729(2016)01-0012-07
中图分类号:O175
文献标志码:ADOl:10.15886/j.cnki.hdxbzkb.2016.0003
